Столкновение со стенкой на скорости 100 км/ч, неприятный сюрприз

Две одинаковые машины, каждая из которых движется со скоростью 100 км/ч, сталкиваются лоб в лоб. Равносильно ли это столкновению с бетонной стеной на скорости 200 км/ч?

Абсолютно упругий велосипедист на скорости 100 км/ч сталкивается лоб в лоб с тяжелым поездом, также двигающимся со скоростью в 100 км/ч. Отскочит ли при этом велосипедист со скоростью 300 км/ч?

Если на вопросы вы ответили "нет, да", то вы правы и ничего нового я вам не расскажу. А остальных приглашаю под кат. Никакой софистики там нет.

Столкновение двух машин

В действительности лобовое столкновение одинаковых машин на скорости 100 км/ч равносильно столкновению с тяжелой стеной на скорости 100 км/ч. Попробуем разобраться.

Рассмотрим центр масс этих двух машин, он находится строго посередине между ними. В ходе столкновения этот центр не смещается. Причем, неважно, будут автомобили абсолютно упругими, абсолютно неупругими или настоящими. Таким образом, в этой точке мы можем поставить виртуальную стену. Заметьте так же, что каждая из двух машин поглотит половину суммарной энергии системы. Точно такую же энергию (mV²/2) поглотит автомобиль, влетающий в стену на той же скорости.

Таким образом, сравнивать это столкновение со столкновением в 200 км/ч неправомерно.

Столкновение велосипедиста с поездом

Покажем, что абсолютно упругий велосипедист отскочит от поезда со скоростью 300 км/ч.

Абсолютная упругость позволит велосипедисту не превратиться в лепешку, потеряв всю свою энергию и скорость, а также путешествовать дальше на лобовом стекле поезда.

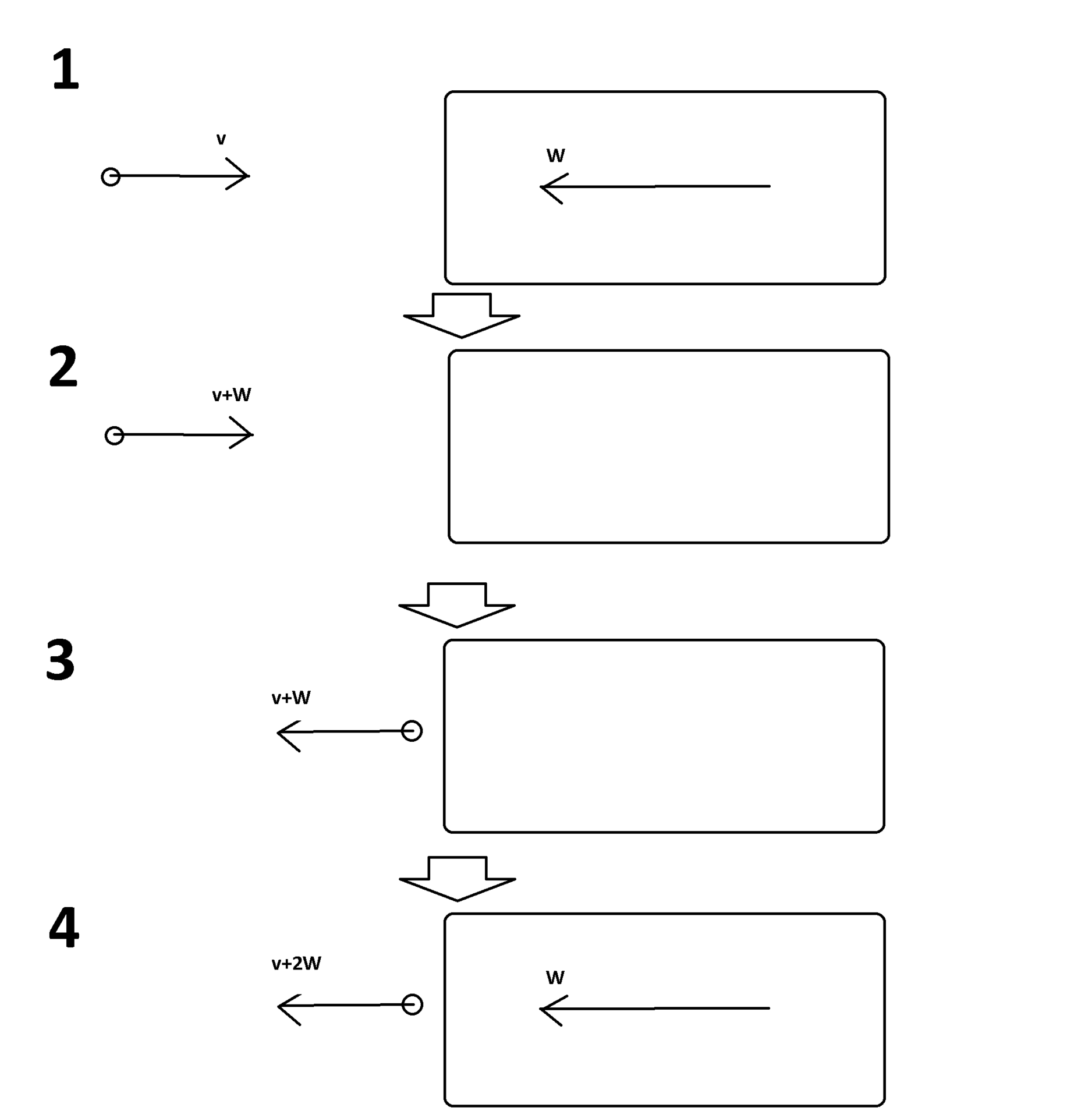
Пусть скорость велосипедиста v, а скорость поезда W. Скорости скалярны (рисунок 1).

1. Для начала перейдем в систему отсчета поезда. По теореме о сложении скоростей он превратится в неподвижный объект, а вот скорость велосипеда увеличится и станет равной v+W (рисунок 2)
2. Так как соударение абсолютно упругое, отскочит велосипедист с той же скоростью v+W (рисунок 3)
3. Перейдем обратно в систему отсчета неподвижного наблюдателя. Все объекты начнут двигаться налево на W быстрее. Поезд снова поедет, а скорость велосипедиста увеличится до v+2W (рисунок 4)
4. А так как в нашем примере v=W=100 км/ч, то скорость велосипедиста станет равной 300 км/ч

Аналогичными рассуждениями с учетом законов сохранения импульсов и энергии выводится формула для скоростей при упругом столкновении


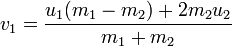
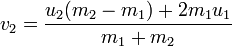
Здесь u_i — скорости до столкновения, v_i — после, а m_i — массы. Скорости векторные. Устремив m₂ в бесконечность, мы получим тот же результат (не забывайте, что у нас u₁ и u₂ разнонаправлены).

Заключение

Я надеюсь, задача не слишком тривиальна для посетителей Хабра, а мои рассуждения оказались понятны Вам. В противном случаем я рискую оказаться заминусованным. Если Вы не согласны с каким-то из пунктов, или он не достаточно понятен, пожалуйста, укажите номер пункта в комментарии.

Приятной пятницы.

Автор: AlexeyVanilov

Источник