
К величию есть только один путь, и этот путь проходит через страдания.
- Альберт Эйнштейн
Эта работа является заключением пятилетнего марафона по поиску самого быстрого способа нахождения минимального точного решения для задачи коммивояжёра в общем виде.
Тут хочу подытожить все опробованные подходы и выбрать лучший по моему мнению.
Мне известны четыре доказанных способа нахождения точного решения ассиметричной задачи коммивояжёра.
1. Метод грубой силы;
2. Метод динамического программирования с меморизацией;
3. Метод ветвей и границ с полным перебором;
4. Методы, основанные на линейном программировании.
Тут мы не будем рассматривать алгоритмы, которые не гарантируют именно точное решение. Хотя многие подходы, основанные на приближённых эвристиках, дают замечательные быстрые результаты, но нет гарантии, что мы получили именно минимальный результат. Так же мы не будем считать расстояние между точками как евклидово пространство. Для евклидова пространства есть алгоритмы, значительно сокращающие область решений. Вдобавок предлагаю считать задачу ассиметричной, даже если это не так. То есть, мы вообще не имеем представления о входной матрице ничего, кроме того, что граф ею образованный не содержит петель, но и это обстоятельство можно игнорировать. Только полный хардкор!
Приступим!
-
Метод грубой силы
Заключается в циклическом переборе всех возможных комбинаций решения задачи с сохранением кратчайшего решения. Метод практически бесполезен в силу неимоверной вычислительной сложности. Для задачи коммивояжёра в общем виде вычислительная сложность метода составляет:
(n-1)! – Количество комбинаций как факториал от числа городов.
Уже при n = 20, нам понадобится перебрать 19! = 121645100408832000 вариантов. Если перебирать по миллиарду комбинаций в секунду у нас уйдёт несколько лет.
Грубо оценим возможность метода как способного решать задачу на не более полтора - два десятка городов.
-
Метод динамического программирования с меморизацией.
Очень крутой метод для решения задачи коммивояжёра. Основное его достоинство состоит в том, что он очень устойчив от входных данных по скорости решения, к тому же неплохо параллелится. В прошлой статье приведена реализация, подходящая для GPU.
Но у данного метода есть ахиллесова пята: требуется экспоненциально большее число памяти для хранения промежуточных вычислений, а именно (n-1)*2^(n-2). Каждое увеличение массива на единицу требует более чем двукратного увеличения объёма памяти.
Для задачи размером n = 30, потребуется 29 * 268435456 * 4 бита - около 29 GB памяти.
Оцениваю способность метода решать задачи до трёх десятков городов.
-
Метод ветвей и границ с полным перебором;
От предыдущих двух подходов метод ветвей и границ отличается тем, что позволяет отбрасывать решения, которые уже на этапе расчёта хуже лучшего найденного. Так мы можем отбросить огромные области дерева решений, значительно сократив время. Однако данный метод очень неустойчив по скорости от набора входных данных. Разные решения на матрице одного размера могут отличаться по времени в десятки тысяч раз и более по скорости расчётов.
В зависимости от реализации метода можно получить значительное превосходство над динамическим программированием, но нет гарантии, что мы сможем дождаться результата для конкретной задачи. В статье я описал собственный вариант алгоритма на C, с которым мне удавалось найди точное решения задачи коммивояжёра в 90% случаях для случайных наборов данных до n = 40.
Приблизительно оцениваю метод как способный решать некоторые задачи размером до n ~ 40 городов.
-
Методы, основанные на линейном программировании.
Задачу коммивояжёра можно сформулировать, как задачу целочисленного линейного программирования. Известно несколько формулировок. Наиболее известные две из них:
Миллера–Таккера–Землина (MTZ)
Данцига–Фалкерсона–Джонсона (DFJ)
В обоих формулировках мы перечисляем все возможные пути между городами целочисленной линейной переменной x = {0, 1}, где x принимает значение 1, если путь выбирается в результирующее решение, 0 в обратном случае.
a) Формулировка Миллера–Таккера–Землина (MTZ)
Описывается следующей схемой:

Из всех моделей, что встречаются как решение задачи коммивояжёра с ЦЛП на просторах сети, эта формулировка самая популярная. Решение находится в один шаг. Мы ищем минимальный цикл, проходящий через все вершины ровно по одному разу. Нижний блок условий запрещает появление циклов меньшего размера.
На тестах MTZ иногда выигрывает у динамического программирования по времени решения, но совсем не устойчивый к разбросу исходных данных. Однако алгоритм не очень требователен к оперативной памяти в отличие от ДП.
Предлагаю считать его не слишком практичным, но всё же способным решать задачи до трёх десятков вершин, иногда немного более.
b) Формулировка Данцига–Фалкерсона–Джонсона (DFJ)
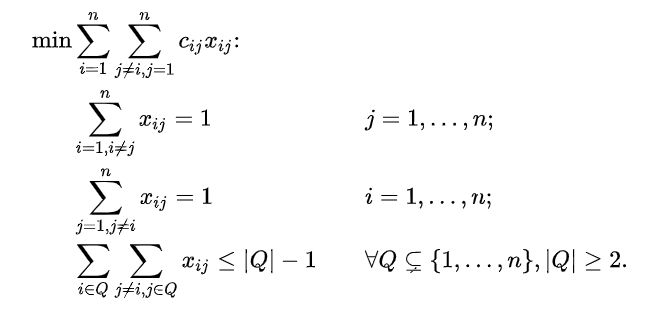
Данная формулировка ещё меньше подходит для нахождения решения задачи коммивояжёра посредством ЦЛП, так как условие исключения подтура создаёт экспоненциально большее число ограничивающих условий. В чистом виде это практически полный перебор. Только мы перебираем не комбинации, а ограничения, а их очень, очень много: (n-1)*2^(n-2).
Оцениваю подход как способный решать задачи до двух десятков городов с натягом.
с) Авторский подход
Если взять за основу модель Данцига–Фалкерсона–Джонсона, а затем несколько изменить подход к выбору ограничивающих условий, то можно получить просто гигантский прирост к скорости решения.
Об этом писал в работах раз, два и три. Возможно мой литературный талант несколько далёк от совершенства и мне не всегда удаётся доносить до читателей основную мысль. Тут мне же хотелось подытожить всё описанное выше и отобразить самый лучший из подходов известных мне.
Основной посыл состоит в том, что мы разбиваем одну большую экспоненциальную задачу на ряд более простых экспоненциальных задач. Но общее время работы последовательности мелких задач значительно меньше, чем решение одной большой задачи.
Чтобы понять насколько значительнее, скажу, что мне удавалось решать точно задачи до полутысячи вершин. Правда это получалось на хороших входных данных, однако и в худшем случае метод бьёт все другие методы, приведённые выше с огромным запасом.
Кратко повторю суть метода: Начало такое же, как у моделей MTZ и DFJ.

Хотя я предпочитаю нумерацию индексов с нуля, а не единицы, но не суть.
Первое отличие состоит в том, что мы не будем указывать верхнюю границу для x.
x = {0, 1} превращается в: x ≥ 0, где x – целое.
Так мы уменьшаем число ограничений линейного решателя на x неравенств. Верхнее ограничение неявно получается из того условия, что число входящих рёбер в каждую вершину и исходящих из неё строго равно одной. Так зачем нам дополнительно ограничивать переменную хij сверху, если сумма всегда не более одного?
Далее мы просто решим систему линейных уравнений и получим опорное решение. Затем проверим, не распалось ли решение на несколько подмножеств, если в результате подмножеств получилось более одного, добавим ограничение в модель и повторим шаг.
Если в результате осталось только одно множество, то считаем его искомым, мы нашли минимальное решение.
Ещё одна оптимизация, которая не учитывалась в прошлых работах: мы добавляем ограничения только для тех подмножеств, размер которых не превышает половины n. Это решение исходит из того, что при получении подмножества размером больше n / 2, должно обязательно существовать иное подмножество размером меньше n / 2, а все такие ограничения мы вносим в модель. Так мы можем слегка уменьшить число ограничений, убрав избыточные условия.
Поскольку мы берём только подмножества размером меньше половины n, нам всегда будет выгоднее выбирать следующую формулировку условия для создания ограничения:
Для каждого подмножества число связей в нём должно быть, как минимум на одно меньше количества вершин в данном подмножестве.
Метод отлично себя чувствует на случайных данных, хуже на симметричных или однородных наборах.
Для объективности приведу одну из худших для метода задачу. Это ряд точек в метрическом пространстве на одинаковом расстоянии друг от друга. Матрица смежности рассчитана через эвклидову норму.

Так как данный пример имеет очень много решений, решателю линейных уравнений нужно перебрать их все.
Реализация метода на Python: github.
Сравнивать модели ЦЛП можно посредством следующей метафоры:
DFJ – всё равно что насыпать огромный террикон ограничений. Ограничений будет очень много, практически нереально получить результат, для этого нужно обработать все условия.

MTZ – как башня - крепость. С наружи каменная кладка условий, что не даёт расползтись множествам. Такую башню проще соорудить чем насыпать просто гору земли аналогичной высоты, но всё же достаточно много работы.

Авторский подход – Можно сравнить с железобетонным каркасом современного здания. Мы поэтажно заливаем слой за слоем, добавляя всё новые ограничения, которые соответствуют уже найденным решениям. Благодаря такому подходу мы можем строить очень высокие строения, считай находить решения большего размера за то же время.

Резюме:
Мы прошлись по методам получения точного решения задачи коммивояжёра в общем виде.
Все рассмотренные подходы являются экспоненциальными по времени от размера исходных данных! Однако время необходимое на решение может быть очень разным в зависимости от метода.
Грубо оцениваю возможности методов, как способных решать задачи размерности n от числа вершин графа.
1. Метод грубой силы не более 15 - 20
2. Метод динамического программирования с меморизацией не более 30
3. Метод ветвей и границ с полным перебором не более 30 - 40
4. Методы, основанные на линейном программировании:
a) DFJ не более 20
b) MTZ не более 30 - 35
c) Авторский подход от 50 в худшем случае и более 500 в лучшем.
Выводы предлагаю сделать самим.
Благодарю за внимание!
Автор: rebuilder





