Нейронные сети для планирования движения беспилотных автомобилей

Планировщик движения беспилотного автомобиля — это алгоритм-помощник, который общается с другими участниками движения посредством манёвров. То есть он действует так, чтобы другим было понятно, куда поедет беспилотник, и сам по действиям других пытается определить, кто куда будет двигаться и почему.

В диалоговых системах совсем недавно произошла революция из-за появления ChatGPT. В беспилотных автомобилях революции, к сожалению, пока не произошло, но если это случится, то как раз в той области, про которую будет мой рассказ.

В этой статье вас ждут детальный разбор логики движения беспилотника, примеры свёрточных и трансформерных архитектур моделей для предсказания движения и много формул для расчёта вероятных траекторий других машин и пешеходов. А ещё я расскажу, в чём преимущества машинного обучения перед эвристиками и чем может помочь Reinforcement Learning. 

Как работает система восприятия в беспилотнике

Глобальная задача в проектировании беспилотных автомобилей — сделать их такими, чтобы сторонний наблюдатель не мог отличить их поведение на дороге от поведения обычной машины. По сути, это задача автоматизации человеческого труда. Поэтому прежде чем говорить о планировщике в беспилотном транспорте, разберёмся, как водит автомобиль человек.

Считается, что во время управления автомобилем водитель непрерывно совершает четыре действия:

• наблюдает (смотрит по сторонам и следит за дорожной обстановкой);

• прогнозирует (пытается понять, на какой объект или движение нужно реагировать); 

• оценивает приоритеты и принимает решения (приоритизирует дорожные события и определяет своё поведение);

• маневрирует (управляет акселератором, тормозит, поворачивает руль и так далее).

На схеме это можно изобразить так:

Рассмотрим для примера простую дорожную ситуацию. Водитель подъезжает к пешеходному переходу — на дороге соответствующая разметка, есть указательные знаки. Справа появляется пешеход за тёмной машиной. В динамике видно, что он собирается переходить дорогу. В стандартной ситуации водитель должен притормозить и пропустить пешехода.

Но бывают ситуации сложнее: например, водитель едет на высокой скорости и следом за ним на такой же скорости другой автомобиль. Здесь нужно принять решение: экстренно остановиться или, наоборот, ускориться, чтобы быстрее проскочить пешеходный переход. Решение принимается динамически на основе человеческого опыта. 

Классическая архитектура ПО, управляющего беспилотным автомобилем, повторяет те же четыре действия, которые выполняет водитель.

Система восприятия смотрит по сторонам и пытается понять, что происходит вокруг машины. Система предсказания движения для каждого движущегося объекта (других автомобилей или людей) пытается спрогнозировать траекторию, по которой они будут двигаться. Планировщик прокладывает оптимальный маршрут с учётом знаний о том, как будет развиваться дорожная ситуация. Система управления перекладывает запланированную траекторию в команды управления машиной — акселератором, тормозом и поворотами руля. 

В этой статье мы будем говорить о двух средних блоках — системе предсказания движения и планировщике. Но чтобы лучше разобраться с ними, надо немного рассказать о системе восприятия, потому что она определяет, как будет работать система предсказания движения. 

У человека есть глаза и уши, с помощью которых он наблюдает за тем, что происходит вокруг. У беспилотника вместо глаз и ушей сенсоры. Их обычно три типа: лидары, радары и камеры. Они размещаются по периметру беспилотника так, чтобы в каждую точку смотрело хотя бы два типа сенсоров, и обеспечивают обзор в 360°. 

На рисунке справа мы видим изображения с камер беспилотного автомобиля (далее — беспилотник), а слева — виртуальное представление мира вокруг беспилотника, которое строит система распознавания. В нём есть дорога, разметка по полосам, которая определяет, как можно перестраиваться во время движения. Есть пешеходные переходы и светофоры, сигналы которых нужно распознавать на ходу. Есть динамические объекты (машины и люди), представленные в виде 3D-боксов с различными атрибутами, такими как текущая скорость, ускорение, тип объекта. Ещё есть статические объекты, представленные в виде гридов — например, остановочный павильон, обозначенный фиолетовой рамкой. 

Дорожную инфраструктуру, которая не меняется, можно положить в HD-карту, похожую на привычные пользовательские карты, только объекты в ней описаны с более высокой точностью. Например, в ней есть граф отдельных полос с топологией, с какой полосы на какую можно перестраиваться. Чтобы использовать знания из HD-карты, нужно уметь находить своё текущее положение на ней. За это отвечает модуль локализации.

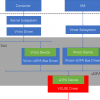
С учётом всего вышесказанного первый блок нашей исходной схемы архитектуры софта беспилотника можно представить так: 

Классический подход к планированию движения

Перейдём к следующему блоку в схеме — системе предсказания движения. С точки зрения этой системы нет особой разницы между движущимися объектами — людьми и автомобилями. Будем называть их одним общим термином агенты. 

На вход в систему поступает сцена — то самое виртуальное представление мира вокруг беспилотного автомобиля, которое построила система восприятия. В идеале на выходе для каждого агента должна быть предсказана траектория — последовательность точек, в которых окажется агент в следующие моменты времени. Предсказания обычно считаются по равномерной сетке, скажем, с шагом 0,1 секунды для времени с 0 до некоторого T — фиксированного горизонта предсказания (гиперпараметра системы).

Но как мы знаем из фильмов про Терминатора, будущее не определено, поэтому предсказывать для каждого агента единственную истинную траекторию — не самая хорошая идея. По этой причине будем требовать от системы предсказания движения выдавать каждому агенту на выходе N траекторий, а также некоторое распределение вероятностей реализации этих траекторий. 

Для такой системы можно строить метрики и оценивать качество её работы. Чаще всего используются следующие:

• minADE (Average Displacement Error или средняя ошибка по траектории) — для каждой из N предсказанных траекторий посчитать среднюю ошибку по точкам в траектории и взять минимум среди получившихся N значений.

• minFDE (Final Displacement Error или ошибка для последней точки траектории) — для каждой из N предсказанных траекторий посчитать ошибку для последней точки траектории и взять минимум среди получившихся N значений.

• miss rate — бинарная метрика, указывающая на то, существует ли среди N предсказанных траекторий хотя бы одна, которая лежит в некотором коридоре от истинной траектории. Если существует, то miss rate для этого агента равен нулю, в противном случае он равен единице. Ширина коридора является гиперпараметром метрики. 

• mAP (mean Average Precision или средняя точность) — интегральная метрика качества, которая рассчитывается с учётом вероятностей предсказанных траекторий. Это та же самая метрика, которая используется в задаче детекции объектов — площадь под кривой precision-recall. Разные значения точности и полноты рассчитываются при варьировании порога на минимальную вероятность траекторий. Предсказанная траектория считается правильной, если она лежит в некотором коридоре от истинной траектории. Ширина коридора, как и в случае метрики miss rate, является гиперпараметром.  

Раньше считалось, что систему предсказания движения можно построить без использования машинного обучения. Для этого есть две популярные эвристики, с помощью которых можно предсказывать движение с относительно хорошей точностью. 

Первая эвристика связана с физическими ограничениями на движения агентов. Например, можно предположить, что агенты двигаются с постоянным ускорением, и с помощью простых формул из школьной физики экстраполировать текущее положение агентов на сцене в будущее. На горизонте 1–2 секунды эта модель будет давать неплохие результаты. 

Вторая эвристика предполагает, что все машины обычно соблюдают ПДД. Их можно проассоциировать с полосами в HD-карте и считать, что они поедут туда, куда ведут эти полосы. Эта эвристика позволяет получать грубое приближение для долгосрочного предсказания движения агентов. 

Несмотря на то, что у этих эвристик вполне естественное происхождение и они связаны с тем, как человек прогнозирует движение других автомобилей, их базовые предположения могут нарушаться. Для более общей модели нужно использовать методы машинного обучения. 

Как обучать модель для предсказания движения

Для каждого агента существует бесконечное множество траекторий движения, на котором определено некоторое распределение вероятностей. Наша задача — восстановить это распределение. Примеры такого распределения — траектории агентов, которые мы наблюдаем в реальной жизни.

Введём вероятностную модель. В данной задаче в качестве неё можно использовать модель смеси гауссовских распределений. Гауссианы будут определены на векторах, представляющих набор точек, из которых складывается траектория. Для упрощения моделирования предположим, что точки траектории — это независимые случайные величины. В таком случае многомерная гауссиана факторизуется на гауссианы по отдельным точкам траектории. Формула правдоподобия траектории агента будет выглядеть так: 

В этой формуле N — число компонент смеси, х — траектория агента, правдоподобие которой мы и считаем, Т — число точек в траектории, p — вероятность компоненты смеси, μ и Σ — параметры гауссиан. Таким образом, задача предсказания траектории движения агента сводится к задаче предсказания параметров p, μ и Σ для каждого агента. 

Дальше мы будем обучать нейронную сеть, которая будет по сцене предсказывать параметры распределения для каждого агента. Приятной особенностью решаемой задачи является то, что для обучения нейронной сети не нужно вручную размечать данные: просто отправляем беспилотный автомобиль кататься по дорогам и записывать обстановку вокруг него и то, по каким траекториям движутся агенты. При этом у каждого агента будет известна ровно одна траектория — то, как он фактически двигался. Задача обучения будет сводиться к оптимизации правдоподобия этих траекторий.

Однако при обучении нейросети правдоподобие траекторий будет оптимизироваться не по общей формуле, а учитывать текущие результаты предсказания параметров распределения. Для каждой траектории среди компонент смеси будет выбрана та, которая лучше всего описывает наблюдаемую траекторию. Именно её параметры и будут оптимизироваться: вес этой компоненты будет повышаться (первое слагаемое в формуле выше), а параметры μ- и Σ-гауссиан в этой компоненте будут сдвигаться так, чтобы увеличилось правдоподобие траектории относительно выбранной компоненты.

Архитектуры для предсказания движения

Мы определились с тем, что должно быть на входе и на выходе нейронной сети, предсказывающей движение агентов. Теперь разберёмся, как может быть устроена сама сеть.

Несколько лет назад был бум свёрточных нейронных сетей. Наша задача хорошо сводится к ним. Можно считать, что беспилотный автомобиль живет в двумерном мире на плоскости дороги. Грид статических препятствий — это пример представления, поверх которого могут работать свёртки. Остальные элементы сцены (3D-боксы для агентов, граф полос, положение и состояние светофоров) также можно привести в формат картинки с помощью процедуры растеризации (то есть перевести в двухмерное пространство). Получившиеся картинки впоследствии можно конкатенировать. 

Конкретные архитектуры, решающие рассматриваемую задачу, похожи на архитектуры детекторов объектов на картинках. В них есть encoder-decoder backbone, дающий карту признаков. Из неё с помощью операции roi-pooling для каждого агента, зная его геометрическое место на карте, можно получить вектор признаков. Из этих признаков дальше предсказываются нужные параметры распределения траекторий. 

Схема работы свёрточных нейросетей может выглядеть так:

Но бум свёрточных сетей сменился бумом трансформеров. Решаемая задача так же хорошо ложится и на архитектуру трансформерных сетей — причём даже лучше! Если для обучения свёрточных сетей нужно было растеризировать все объекты на сцене, то в трансформерах элементы сцены можно подавать в сеть напрямую. С помощью многослойного перцептрона эти элементы будут переводиться в новое пространство признаков, поверх которого можно будет выполнять операцию attention и выучивать векторы признаков для агентов, из которых предсказывать параметры распределений на траектории.

Схема трансформерной сети выглядит так:

Планирование траектории как задача оптимизации

Теперь поговорим о следующем блоке в архитектуре софта беспилотника — планировщике траекторий. Опять же будем считать, что беспилотный автомобиль живёт в двумерном мире на плоскости дороги. На эту плоскость можно нанести регулярную сетку, например, с шагом 10 сантиметров и соединить некоторые пары узлов сетки направленными рёбрами. Наличие ребра между двумя узлами будет означать, что есть способ попасть из одной точки в другую. В итоге мы могли бы получить следующий граф:

Это позволяет свести исходную задачу поиска оптимальной траектории на плоскости к задаче поиска оптимального пути в графе между двумя узлами: начальным положением автомобиля и целевой точкой, куда хотелось бы приехать. 

Назначим каждому ребру вес: насколько маневр, подразумеваемый этим ребром, приемлем для движения беспилотного автомобиля. Зная эти веса, можно запустить один из методов поиска оптимального пути на графе, например А*. 

Решение, которое будет давать этот метод, может быть субоптимальным в терминах оптимизации в исходном пространстве возможных траекторий из-за дискретизации пространства поиска. Поэтому получившееся решение полезно сгладить одним из методов непрерывной оптимизации.

Главный плюс этого подхода к планированию траекторий — его интерпретируемость. Всегда можно объяснить, почему получилось то или другое решение. Однако у этого подхода есть и ряд серьёзных недостатков.

Проблемы подхода

Первая проблема — это способ определения весов отдельным рёбрам. Рассмотрим следующую схему:

Справа на схеме находится тротуар, на который не хотелось бы выезжать, слева — другой агент, с которым мы не хотим сталкиваться. Мы можем выкинуть рёбра, которые ведут нас в эти направления (обозначены красным цветом). Это строгие ограничения, которые можно легко вносить в систему и гарантировать их исполнение.

Но есть и нестрогие ограничения. Например, нам бы хотелось держаться на безопасном расстоянии от других агентов, избегать резких разгонов, торможений, крутых поворотов. Но как уравнять между собой вклады различных эвристик для нестрогих ограничений? Как это сделать аналитически — непонятно. Остается либо отдать эту задачу эксперту, который будет решать её методом проб и ошибок, либо использовать машинное обучение и настраивать веса рёбрам на основе данных.

Отдельный вопрос про правила дорожного движения — являются ли они строгими ограничениями? По идее, ПДД нарушать нельзя, но в отдельных случаях без этого невозможно передвигаться. Например, двойную сплошную пересекать нельзя, но если в нашей полосе ДТП, то нормальный водитель не будет ждать, пока эвакуатор увезёт повреждённый автомобиль, а аккуратно объедет препятствие по встречке. По сути, это нарушение ПДД, но вести себя в данной ситуации иначе — странно. И такой случай нужно как-то внести в систему планирования. 

Вторая проблема связана с тем, что на самом деле нейросетевая модель выучивает предсказания движения агентов, про которую я рассказывал выше. Ведь на поведение других участников движения влияет то, как себя ведём мы во время движения. В терминах вероятностного моделирования сеть учится максимизировать правдоподобие траекторий из проездов, обусловленных на некоторое е —  наше поведение в этих проездах. 

Из этого замечания вытекают два следствия: 

• Когда планировщик пытается проложить оптимальную траекторию так, чтобы не помешать другим агентам, он на самом деле занимается некоторой реверс-инженерией того поведения, которое заложено в модель. Это то поведение, которое было при записи данных для обучения.

• Если планировщик не справляется с задачей воспроизведения референсного поведения, то мы начинаем ехать иначе. Агенты тоже начинают реагировать иначе и их движение начинает расходиться с моделью.

Таким образом, для правильной работы модуля предсказания движения важно, чтобы поведение машины при записи данных было максимально близко к тому, какое поведение будет при применении модели.

Третья проблема классического планировщика связана с тем, что для каждого участника движения предсказывается не одна траектория, а несколько. Но беспилотный автомобиль может оказаться, например, в пробке, где рядом с нами будет очень много агентов, и у каждого будет, скажем, по четыре траектории. И если модуль планирования будет с этим работать в консервативном сценарии, то велика вероятность, что мы никуда не поедем, потому что везде будет пересечение с возможной траекторией другого агента.

Эту проблему решают фильтрацией траекторий. Если каждая траектория по отдельности, скорее всего, имеет смысл, то в совокупности все траектории не всегда выполнимы. Как вариант можно завести ML-классификатор, который будет принимать пару траекторий разных агентов и определять, возможна ли эта пара или ее не нужно рассматривать.

Есть ещё одна проблема, которую стоит упомянуть. Допустим, мы едем по главной дороге, справа — примыкание второстепенной, и какой-то агент (желтая коробка на картинке) немного высунулся на нашу полосу и остановился. Модуль предсказания движения выдал для него четыре траектории. Самая вероятная — он останется стоять. Три другие указывают на его движение с разной скоростью.

Какое поведение должен спланировать беспилотный автомобиль в этой ситуации? Если мы будем предполагать самое худшее поведение агента, то беспилотник должен его пропустить. Кроме того, целых три траектории указывают на то, что агент поедет дальше. Но с другой стороны, беспилотный автомобиль находится на главной дороге, почему он должен пропускать агента со второстепенной? Беспилотник может сдвинуться влево и продолжить движение по своей полосе, агент его пропустит.

В данном примере движение агента целиком зависит от наших действий: если мы притормаживаем, водитель понимает, что можно ехать, и трогается. А если не пропускаем, он стоит и ждёт нас. То есть здесь нет четырёх равных сценариев движения агента и модель предсказания движения агента должна быть другой.

Как решить эту проблему? Можно пытаться классифицировать предсказанные траектории и определять, какому нашему манёвру они соответствуют. Или можно заранее обучить классификатор, который будет отвечать на вопрос, стоит ли нам пропустить агента со второстепенной дороги. 

Альтернативный подход к планированию движения

Итак, в классическом подходе сначала решается сложная задача предсказания движения агентов, строятся мультимодальные распределения, обучаются трансформеры, чтобы потом можно было использовать простой и интерпретируемый оптимизационный планировщик. Однако это всё равно не спасает от проблем, с которыми приходится бороться разными эвристиками или обучением вспомогательных ML-алгоритмов. 

А если в планировщике сразу использовать машинное обучение и предсказывать идеальную траекторию самого беспилотного автомобиля? В целом это почти та же задача, что и предсказание поведения агентов, с тем же входом и похожим форматом выхода. Единственное отличие в том, что в задаче предсказания движения агентов мы не знаем, куда они хотят попасть. А когда мы определяем свою траекторию, у нас есть финальная точка, в которой мы хотим оказаться, и нам нужно подать эту точку на вход нейросети.

У такого подхода есть разные приятные свойства. Например, упрощается выход на новую локацию. Если нужно запустить эксплуатацию беспилотного автомобиля в новой стране или городе со своими типичными правилами поведения на дорогах, то не нужно будет настраивать какие-то константы и эвристики в коде. Достаточно собрать датасет типичных траекторий, как ездят в этом городе, обучить нейросеть, и всё получится (правда, в теории). 

Использование нейросетей в планировщике также существенным образом упрощает кодовую базу. Мы выкидываем разные эвристики определения весов рёбер — остаётся просто нейронная сеть. 

Но есть у этого подхода и минусы. Во-первых, мы теряем гарантии на физичность запланированной траектории. Если в классическом планировщике мы строили рёбра исходя из предположений о возможности проехать по этой траектории, то теперь мы предсказываем какую-то последовательность точек без гарантии, что мы сможем по ним проехать. Но это проблема формулировки задачи. Можно предсказывать не точки в траектории, а, например, последовательность команд управления машиной.

Во-вторых, недостаток ML-планировщика в том, что машинное обучение — это всё же статистический метод. Он рано или поздно он выдаст ошибку — например, траектория поведёт беспилотник куда-нибудь в стену. Поэтому траектории, которые выдаёт ML-планировщик, обязательно нужно валидировать на предмет того, что они действительно соблюдают все строгие ограничения.

И ещё одна проблема — все строгие ограничения, включая ПДД, нужно выучить статистически. Например, нужно выучить правило, что нельзя ехать на красный свет. Если в классическом планировщике это явно контролируется на этапе генерации рёбер графа, то здесь надо собирать датасет под каждый случай. Это, конечно, неприятно, но не смертельно. 

Behavioral Cloning и его проблемы

Читатели, знакомые с методами обучения с подкреплением (Reinforcement Learning), могли заметить, что предлагаемая схема обучения ML-планировщика называется поведенческим клонированием (Behavioral Cloning) — мы учим сеть воспроизводить некоторое экспертное решение задачи.

У поведенческого клонирования есть типичная проблема — DAgger problem. Например, если мы попросим водителя ехать прямо, то он, скорее всего, будет ехать просто ровно по центру полосы. Если же мы обучим на этой траектории ML, то планировщик, скорее всего, будет предсказывать траекторию с небольшими отклонениями от прямой линии:

С одной стороны, ошибка такой траектории может быть довольно низкой. Но когда мы начнём по ней двигаться, то в моментах отклонения от прямой линии будет запускаться новый цикл планирования, где мы будем предсказывать новую траекторию. А так как у нас руль будет немного отклонён вправо или влево и такого положения нейросеть у экспертов не видела, то из этого состояния планировщик может завести нас куда угодно — в стену, на тротуар, на встречку. Это может произойти из-за того, что таких примеров в обучающем датасете не было.

Что с этим делать? Первое решение — пытаться как-то искажать реальные экспертные данные и показывать нейросети, что из отклонённого от прямой линии состояния нужно возвращаться в центр полосы. Это более инженерный подход, потому что нам нужно поменять не просто своё позиционирование, но и в целом всю сцену. 

Второе решение — это closed-loop-обучение (обучение с замкнутым циклом обратной связи). При таком обучении симулируется режим применения сети. В процессе обучения генерируется первая траектория, и беспилотный автомобиль виртуально продвигается по её префиксу. Далее генерируется траектория из нового состояния, и снова беспилотник виртуально продвигается по префиксу. Процедура повторяется, пока не соберем траекторию необходимого размера. По ней считается функция потерь с экспертной траекторией.

Чтобы пойти вторым путём, нужен симулятор, который бы продвигал виртуальный беспилотник по запланированному префиксу и изменял окружающую сцену в соответствии с новым положением. Сделать такой симулятор — это сама по себе довольно сложная задача.

Подход End-to-end

Вернёмся к архитектуре софта беспилотного автомобиля. Если мы внедряем ML-планировщик, то в схеме объединяются два блока: система предсказания движения и собственно планировщик. Их заменяет один блок с нейронной сетью, который сразу выдаёт траекторию беспилотного автомобиля. Она принимает на вход данные о сцене и возвращает траекторию.

Однако в схеме появляются два последовательных блока, так или иначе основанных на нейронных сетях: система восприятия и ML-планировщик. Можно ли их объединить? Можно. В итоге получим ещё одну альтернативную схему работы беспилотника, основанную на end-to-end подходе:

В чём сложность такого подхода? Качество планировщика обычно проверяется в симуляторе. При end-to-end подходе нужно уметь симулировать лидарные и радарные облака, картинки и всё то, что подается в сеть на вход. Чтобы делать это хорошо, нужно написать свой аналог GTA V, а это довольно сложная задача. Намного проще разбить сеть на две части, обучать ML-планер поверх внутреннего представления сцены и симулировать в тестах именно его. Поэтому в end-to-end мы пока не идем.

И ещё немного про данные

И наконец, как и в любом обучении ML-моделей, при улучшении качества можно вкладываться в совершенствование методов обучения, а можно улучшать пайплайн сбора данных. ML-планировщик не исключение. 

У Waymo есть хорошая статья, где авторы поделились исследованиями, насколько важно качество данных при обучении. Оказывается, если правильно подойти к данным и построить систему, которая ранжирует их по степени сложности, и обучать планировщик просто поведенческим клонированием (Behavioral Cloning), но на 10% самых сложных сценариев, то такой планировщик будет работать примерно так же, как обучение с подкреплением (Reinforcement Learning) на всех данных. Однако эти направления взаимодополняют друг друга: обучение с подкреплением на 10% сложных сценариях работает ещё лучше. 

Reinforcement Learning особенно важно, когда мы переходим к самым сложным сценариям — топ-1% сложных сцен. Здесь польза от обучения с подкреплением начинает доминировать в сравнении с пользой от работы с данными. Сложные сценарии обычно редкие, в них сложно попасть на этапе сбора экспертных данных, и это естественным образом ограничивает качество, которое можно получить при обучении через поведенческое клонирование. А вот при обучении с подкреплением в них можно будет дополнительно попасть из-за самой процедуры обучения.

---

Область применения нейронных сетей в беспилотных автомобилях не ограничивается только системой распознавания. Нейронные сети широко применяются для предсказания движения агентов, а также начинают использоваться для планирования собственного движения беспилотника. 

Специфика этих нейронных сетей заключается в работе поверх структурного представления сцены, а не на сырых данных с лидаров, радаров и камер. Это обусловлено необходимостью уметь симулировать входные данные в эти сети для тестирования планировщика. Но возможно по мере развития генеративных сетей задача генерации фотореалистичных данных с сенсоров беспилотника будет решена, и весь пайплайн на борту беспилотника можно будет заменить на единую end-to-end-сеть.