Пишем свой физический движок с преферансом и барышнями

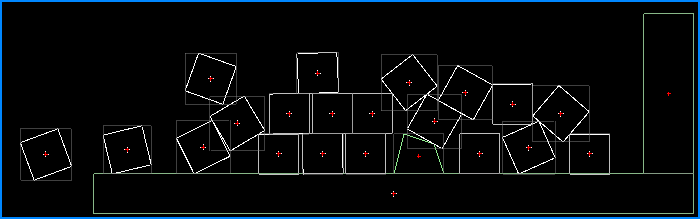
Привет дорогой друг! В прошлой статье я говорил, что больше не буду затрагивать тему 2D игр на XNA. Пожалуй, я вас обманул, но не совсем. Многие начинающие геймдевелоперы используют в своих физических головоломках — физический движок Box2D, о нем довольно много писали на хабре. Да что уж там новички, многие довольно опытные геймдевелоперы — его используют. Но вот мало кто знает, как на самом деле он работает. Остальное под хабракатом.

В этой статье я постараюсь подробно описать процесс создания каркаса физического движка. Конечно, получиться не совсем Box2D: различные хеш оптимизации, отсечения не будут описываться в данной статье, но будет понятно, как он работает.

Общие принципы. Как это вообще работает?

Обычное игровое приложение каждый кадр выполняет примерно такую последовательность действий:

• Воздействуем на физический мир
• Обновляем физический мир
• Отрисовываем его новое состояние
• Повторяем

Самый интересный для нас шаг в этой схеме — второй. Именно здесь и происходит вся магия физического движка — он определяет, в какое состояние перейдёт физическая система в следующий момент времени, спустя dt (короткий промежуток времени). Этот шаг, в свою очередь, уже внутри движка разбивается ещё на три подшага:

• Обнаружение столкновений
• Разрешение столкновений
• Интегририрование

И вот именно их мы и будем реализовывать. Эти действия в существенной степени независимы и, реализовав их, мы получаем нехитрый физический движок.

Начнем с устройства физического движка, который мы будем писать. Наша цель — написать физику твердых тел на основе импульсов. В идеале нам хотелось бы, чтоб тело могло быть любой формы, т.е., например, такой:

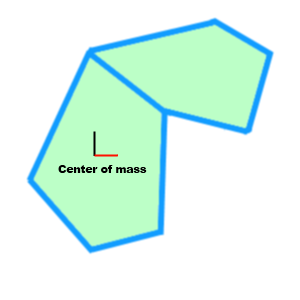
На самом деле описать такую форму довольно сложно, и движки, работающие на «невыпуклых» формах, найти очень сложно, не говоря уже о 3D. Поэтому мы создадим такую систему, что тело можно будет представить любой сложной формой с помощью простых форм.

Теперь разъясню составляющие физического тела. Само «тело» в нашем движке будет просто точка, имеющая центр масс. Эта точка будет перемещаться под действием различных сил, например, гравитации. Вокруг нее (точки) могут быть «навешаны» формы. В данной статье будут рассмотрены формы выпуклых полилиний (полигонов). После прочтения статьи — вы можете добавить и свои шейпы (формы), например, различные квадратики и кружечки. При процессинге (обработке физических тел в Update) мы будем искать шейпы, которые пересеклись, т.е. «сколизились» (collision — англ., пересечение), затем искать три основных необходимых для минимального импульсного физического движка величины, это — нормаль, вдоль которой произошла коллизия, глубину проникновения одного объекта в другой и точку контакта тел.

Допустим, имеем контакт:

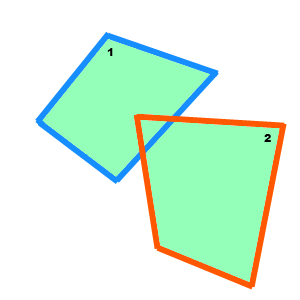
А вот коллизия двух выпуклых полилиний:

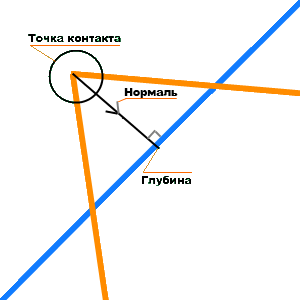
Выпуклость полилиний упрощает нам задачу поиска коллизии. Тело должно иметь массу, момент инерции, линейную и угловую скорости, линейное и угловое ускорение, позицию в мировом пространстве (координаты центра масс), коэффициенты трения и упругости, а также текущий угол поворота.

С теорией пока все, начнем реализовывать. Сразу оговорюсь, что я покажу три основных класса и дам максимально развернутую информацию по ним в виде комментариев.

Т.к. в XNA многие операции над векторами у нас уже есть — мы его просто расширим, листинг расширяющегося класса:

namespace phys.V2Math
{
    public static class V2Extend
    {
        public static float PerpDot(this Vector2 self, Vector2 vector) // перпендикуляр с скалярным произведением
        {
            return self.X * vector.Y - self.Y * vector.X;
        }

        public static Vector2 Perp(this Vector2 self) // перпендикуляр
        {
            return new Vector2(-self.Y, self.X);
        }

        public static float Dot(this Vector2 self, Vector2 vector) // скалярное произведение
        {
            return self.X * vector.X + self.Y * vector.Y;
        }

        public static Vector2 Negative(this Vector2 self) // отрицательный вектор
        {
            return new Vector2(-self.X, -self.Y);
        }

        public static Vector2 Rotate(this Vector2 self, Vector2 vector) // вращение вектора
        {
            return new Vector2(self.X * vector.X - self.Y * vector.Y, self.X * vector.Y + self.Y * vector.X);
        }

        public static Vector2 Normalize2(this Vector2 self) // нормирование вектора
        {
            Vector2 vector = self;
            vector.Normalize();
            return vector;
        }
    }
}

Теперь нам нужен класс, который будет отвечать за сами объекты тел, создадим его:

namespace phys
{
    public class Body
    {
        public Vector2 position; // позиция
        public Vector2 velocity; // ускорение
        public float angle;   // текущий угол в радианах
        public float w;   // угловое ускорение в радианах
        public float m;   // масса
        public float f;   // трение
        public float e;   // упругость
        public bool isStatic;  // статичный ли объект

        internal float i;   // момент инерции

        public List<Poly> shapes; // формы данного тела

        // функция накладывает импульс на тело
        // j - импульс (вектор)
        // r - точка приложения импульса в локальных координатах
        public void ApplyImpulse(Vector2 j, Vector2 r)
        {
            if (isStatic)
                return;

            velocity += j / m;
            w += r.PerpDot(j) / i;
        }

        
    }
}

Саму интерацию (движения тела, поворот тела, etc) мы будем просчитывать в другом классе, который будет ответственен за физику в целом, назовем этот класс: "World".

Этот класс в себе будет хранить список тел, будет содержать метод step, который и будет у нас за все отвечать. Рассмотрим класс:

namespace phys
{
    public class World
    {
        public static float c_Depth = 0.1f;
       
        public Vector2 gravity;
        public List<Body> bodies;

        public World(Vector2 gravity)
        {
            this.gravity = gravity;
            bodies = new List<Body>();
        }

        public void CreateDemo() // создаем демо-сцену
        {
            ...
        }

        public Body Body2;
        public Body sBody;

        //Обновляем позицию, ускорение и угол тела за промежуток
        // времени dt и гравитацией gravity, действующей на тело
        // в нормальной среде (вакум)
 
        public void Step(float delta, int interations)
        {
            float dt = delta / (float)interations;

            for (int interation = 0; interation < interations; interation++)
            {
                
                foreach (Body body in bodies)
                {
                    if (!body.isStatic)
                        body.velocity += gravity * dt;        // добавляем гравитацию

                    body.angle += body.w * dt;            // обновляем угол поворота
                    body.position += body.velocity * dt;  // обновляем позицию тела

                    foreach (Poly poly in body.shapes)
                    {
                        // вычисляем кос и син угла поворота тела
                        poly.rot = new Vector2((float)Math.Cos(poly.body.angle), (float)Math.Sin(poly.body.angle));

                        for (int i = 0; i < poly.VertexsCount; i++)
                        {
                            // находим координаты вершин (мировые)
                            poly.v[i] = poly.body.position + poly.v_base[i].Rotate(poly.rot);

                            // нормаль и скаляр для ребер
                            poly.ed[i].n = poly.ed_base[i].n.Rotate(poly.rot);
                            poly.ed[i].d = poly.body.position.Dot(poly.ed[i].n) + poly.ed_base[i].d;
                        }

                        poly.broadphase = Poly.GetBroadphase(poly);
                    }
                }

                foreach (Body body1 in bodies)
                    foreach (Body body2 in bodies)
                    {
                        if (body1 != body2)
                        {
                            bool collided = false;

                            foreach (Poly poly1 in body1.shapes)
                            {
                                foreach (Poly poly2 in body2.shapes)
                                    if (Broadphase.Collided(poly1.broadphase, poly2.broadphase))
                                    {
                                        Collide(body1, body2);
                                        collided = true;
                                        break;
                                    }

                                if (collided)
                                    break;

                            }
                            
                        }
                    }
            }
        }

        public bool Collide(Body b1, Body b2)
        {
            foreach (Poly poly1 in b1.shapes)
                foreach (Poly poly2 in b2.shapes)
                    if (Poly.FindCollision(poly1, poly2))
                        return true;

            return false;
        }

        public IEnumerable<DebugLine> getDebugLines() // получем линии для отрисовки объектов
        {
		...
        }
}

Теперь рассмотрим код шейпа (Poly):

namespace phys
{
    public class Poly
    {
        public Vector2[] v;           // мировые координаты вершин
        public Vector2[] v_base;       // локальные координаты вершин

        public Edge[] ed;          // мировые данные о гранях
        public Edge[] ed_base;      // локальные данные о гранях
        public Broadphase broadphase;

        public int VertexsCount
        {
            get { return v_base.Length; }   
        }

        public Vector2 rot;    // коссин для поворота вершин
        public Body body;

        public Poly(Body body, Vector2[] vertexs)
        {
            Vector2 a, b;
            
            this.body = body;

            // копируем вершины
            this.v_base = vertexs;
            this.v = new Vector2[VertexsCount];
            this.ed = new Edge[VertexsCount];
            this.ed_base = new Edge[VertexsCount];

            // подсчитываем нормаль и скаляр к ребрам (возможно тут нужен фикс)
            for(int i = 0; i < this.VertexsCount; i++)
            {
                a = this.v_base[i];
                b = this.v_base[((i+1) % VertexsCount)];

                Vector2 someRENAME = ((Vector2)(b - a)).Perp();

                this.ed_base[i].n = someRENAME.Normalize2();
                this.ed_base[i].d = this.ed_base[i].n.Dot(a);
            }


            // присоединяем форму к телу
       
            body.shapes.Add(this);

            Poly poly = this;

            // вычисляем кос и син угла поворота тела
            poly.rot = new Vector2((float)Math.Cos(poly.body.angle), (float)Math.Sin(poly.body.angle));


            for (int i = 0; i < poly.VertexsCount; i++)
            {
                // находим координаты вершин (мировые)
                poly.v[i] = poly.body.position + poly.v_base[i].Rotate(poly.rot);

                // нормаль и скаляр для ребер
                poly.ed[i].n = poly.ed_base[i].n.Rotate(poly.rot);
                poly.ed[i].d = poly.body.position.Dot(poly.ed[i].n) + poly.ed_base[i].d;
            }

            broadphase = Poly.GetBroadphase(this);
        }

        /*
         * Вычисление момента инерции полигона.
         * m-масса тела, verts-вершины полигона, nVerts-их количество
         * Момент инерции всего тела равен сумме моментов инерции всех его форм.
         */

        public float IMoment()
        {
            float sum1, a, b, sum2;
            Vector2 v1, v2;

            sum1 = 0;
            sum2 = 0;

            for (int i = 0; i < VertexsCount; i++)
            {
                v1 = v_base[i];
                v2 = v_base[(i + 1) % VertexsCount];

                a = (v2.X * v1.Y) - (v2.Y * v1.X);
                b = v1.Dot(v1) + v1.Dot(v2) + v2.Dot(v2);

                sum1 += a * b;
                sum2 += a;
            }

            return (body.m * sum1) / (6.0f * sum2);
        }

        /* Суть метода такова: есть процесс, мы его сначала просчитываем от первого полигона в отношении второго,
         * затем наоборот - от второго в отношении первого.
         * Суть процесса заключается в поиске точек одного полигона (суть видно на рисунке в начале статьи, где иллюстрирован контакт двух полигонов),
         * которые лежат внутри второго полигона, если такие точки есть - полилинии пересеклись,
         * причем эта точка и будет точкой контакта.
         * Далее ищем ближайшее к данной точке ребро второго полигона, нормаль к этому ребру и будет нормаль контакта,
         * а расстояние от данной точки до данного ребра и есть глубина проникновения.
         * Таким образом, все три необходимых данных у нас есть,
         * заносим их в структуру контакта и передаем обработчику импульсов тел.
         * А затем выталкиваем тела по нормали, в противоположные стороны для каждого тела, на расстояние,
         * равное половине глубины проникновения.
         * Допустим, мы нашли пересечение полилиний, т.е. одна из точек первого полигона зашла внутрь второго. Напишем функции поиска ближайшего к данной точке ребра.
         * Скалярное произведение векторов хранит их длины, этим и воспользуемся: чем меньше величина скалярного произведения от ребра до точки,
         * тем ближе последняя к нему находится.
         * Функция ищет ближайшее ребро к данной точке.
         */

        public static float EdgeDist(Poly poly, Vector2 n, float d)
        {
            float _m = n.Dot(poly.v[0]);

            for (int i = 1; i < poly.VertexsCount; i++)
                _m = Math.Min(_m, n.Dot(poly.v[i]));

            return _m - d;
        }

        // Находим минимальное расстояние между ребром и точкой полигона
        public static int FindEdgeMinDist(Poly poly, Edge[] ed, int num, ref float _m)
        {
            int _mi = 0;
            float __m, dist;

            __m = Poly.EdgeDist(poly, ed[0].n, ed[0].d);
            if (__m > 0f)
                return -1;

            for (int i = 0; i < num; i++)
            {
                dist = Poly.EdgeDist(poly, ed[i].n, ed[i].d);
                if (dist > 0f)
                    return -1;
                else if (dist > __m)
                {
                    __m = dist;
                    _mi = i;
                }
            }
            _m = __m;
            return _mi;
        }

        // находим какая точка лежит внутри полика
        public static bool PointIn(Poly poly, Vector2 p)
        {
            float dist;

            for (int i = 0; i < poly.VertexsCount; i++)
            {
                dist = poly.ed[i].n.Dot(p) - poly.ed[i].d;
                if (dist > 0f)
                    return false;
            }

            return true;
        }

        /* Ищем точки взаимопроникновения, самая главная функция нашего движка, в ней мы ищем,
         * какими точками полигоны проникли друг в друга, и если проникли,
         * то ищем все необходимые данные для контакта и отправляем на обработку.
         */
        public static void VertsProc(Poly p1, Poly p2, Vector2 n, float d)
        {
            float k;
            // используем абсолютное значение глубины
            d = Math.Abs(d);

            // сначала ищем точки первого полигона внутри второго
            for (int i = 0; i < p1.VertexsCount; i++)
                if (Poly.PointIn(p2, p1.v[i])) // если нашли, то заполняем данные контакта:
                {

                    Contact contact = new Contact();
                    contact.p = p1.v[i];        // точка контакта и есть данная вершина
                    contact.n = n;              // нормаль мы получили из вызывающей функции
                    contact.depth = d * World.c_Depth;  // глубину получили таким ж способом
                    contact.r1 = contact.p - p1.body.position;  // вспомогательные вектора, направлены из // точки контакта в центр масс каждого тела
                    contact.r2 = contact.p - p2.body.position;

                    // далее считаем коэффициент выталкивания тел,
                    // в зависимости от их состояния(статичный или нет)
                    if (p1.body.isStatic)
                        k = 0f;
                    else if (p2.body.isStatic)
                        k = 1f;
                    else k = 0.5f;

                    // расталкиваем тела по нормали в разные стороны на глубину проникновения
                    // учитывая что нормаль направлена относительно 1 тела ко 2
                    p1.body.position -= contact.n * (k * contact.depth);
                    p2.body.position += contact.n * ((1 - k) * contact.depth);

                    // после того, как нашли все данные отправляем их на обработку
                    contact.Solve(p1.body, p2.body);
                }
        }

        /* Далее - функция, которая ищет факт пересечения полигонов (на основе предыдущей функции)
         * и в случае успеха будет вызывать нашу главную функцию поиска точек контакта
         * и передавать ей в качестве параметров найденное ближайшее ребро (а следовательно, и все его данные).
         */
        public static bool FindCollision(Poly p1, Poly p2)
        {
            float min1 = 0f;
            float min2 = 0f;

            int min1_idx, min2_idx;

            min1_idx = Poly.FindEdgeMinDist(p2, p1.ed, p1.VertexsCount, ref min1);
	        if (min1_idx == -1)
                return false;

	        min2_idx = Poly.FindEdgeMinDist(p1, p2.ed, p2.VertexsCount, ref min2);
            if (min2_idx == -1)
	            return false;
            
             if (min1 > min2)
                Poly.VertsProc(p1, p2, p1.ed[min1_idx].n, min1);
                    else
                        Poly.VertsProc(p1, p2, p2.ed[min2_idx].n.Negative(), min2);

            return true;
        }

        public static Broadphase GetBroadphase(Poly poly)
        {
            ...
        }
    }
}

Теперь нужно решить проблему просчета контактов, реализуем класс Contact и метод Solve:

namespace phys
{
    public class Contact
    {
        public Vector2 p;  // координаты точки пересечения 
        public Vector2 n;  // нормаль относительно 1 тела к 2
        public Vector2 r1;  // вектор из 1 тела в точку контакта
        public Vector2 r2;  // вектор из 2 тела в точку контакта
        public float depth; // глубина проникновения 

        // Решаем контакт
        public void Solve(Body c1, Body c2)
        {
            Vector2 v1, v2, vr, t, j;
            float vrn, jn, jnOld, bounce, e, u, mass_sum,
            r1cn, r2cn, vrt, kn, nMass, jtMax, jt, jtOld,
            r1ct, r2ct, kt, tMass, jnAcc, jtAcc;

	     // у статических тел — масса и инерция бесконечны
            float m1 = c1.isStatic ? float.PositiveInfinity : c1.m;
            float m2 = c2.isStatic ? float.PositiveInfinity : c2.m;
            float i1 = c1.isStatic ? float.PositiveInfinity : c1.i;
            float i2 = c2.isStatic ? float.PositiveInfinity : c2.i;

            e = c1.e * c2.e;    // вычисляем общий коэффициент трения поверхностей
            u = c1.f * c2.f;  // и общий коэффициент эластичности

            // {расчет общих коэффициентов может быть другой, например средний арифметический (c1^.f+c2^.f)/2.0}
            jtAcc = 0.0f;
            jnAcc = 0.0f;

            v1 = c1.velocity + (r1.Perp() * c1.w);
            v2 = c2.velocity + (r2.Perp() * c2.w);

            vr = v2 - v1;
            vrn = vr.Dot(n);

            bounce = n.Dot(v2 - v1) * e;
            mass_sum = (1f / m1) + (1f / m2);
            r1cn = r1.PerpDot(n);
            r2cn = r2.PerpDot(n);

            kn = mass_sum + ((r1cn * r1cn) / i1) + ((r2cn * r2cn) / i2);
            nMass = 1.0f / kn;

            jn = -(bounce + vrn) * nMass;

            jnOld = jnAcc;
            jnAcc = Math.Max(jnOld + jn, 0.0f);

            jn = jnAcc - jnOld;
            t = n.Perp();

            vrt = vr.Dot(t); // (0,0)
            t = n.Perp();

            r1ct = r1.PerpDot(t);
            r2ct = r2.PerpDot(t);

            kt = mass_sum + ((r1cn * r1cn) / i1) + ((r2cn * r2cn) / i2);
            tMass = 1.0f / kt;

            // трение
            jtMax = u * jnAcc;
            jt = -vrt * tMass;
            jtOld = jtAcc;
            jtAcc = Math.Min(Math.Max(jtOld + jt, -jtMax), jtMax);
            jt = jtAcc - jtOld;
            j = (n * jn) + (t * jt);

            // накладываем импульсы
            c1.ApplyImpulse(j.Negative(), r1);
            c2.ApplyImpulse(j, r2);
        }
    }
}

Кодом я старался описать основные принципы работы импульсных движков, более разверенуто можно посмотреть все исходном коде.

Итак, подведем итоги. Очевидно, что написать физический движок на основе импульсов в 2D не так сложно, как может показаться на первый взгляд. Удачи в начинаниях!

Исходный код можно скачать тут, а exe-демо тут.

P.S. огромная просьба, об очепятках/ошибках писать мне личным сообщением, не стоит писать комментарии без полезной смысловой нагрузки.

P.S.S.S. если вы хотите, чтобы я осветил одну из тем, связанных с геймдевом — рад видеть вас в личных сообщениях.

Автор: ForhaxeD