Звездное скопление Омега Центавра (Рис.1) с массой в 4 миллиона солнечных имеет радиус около 90 световых. 10 июля 2024 года в журнале Nature была опубликована сенсационная статья об открытии в этом скоплении черной дыры с массой в 8200 раз больше массы Солнца. Главными свидетелями существования этого невидимого объекта оказались быстрые звезды, которые без гравитационного поля массивной дыры должны были покинуть скопление очень быстро - в течение тысячи лет.

Это открытие произошло на фоне современных драматических изменений в космологической парадигме. Шаровые скопления – это интереснейшие объекты, роль которых была ранее значительно недооценена. Судя по всему, именно они отвечают за таинственное соотношение Талли-Фишера. В чем его загадка?
Согласно кеплеровскому закону, который знают даже школьники, квадрат скорости V кругового вращения тел вокруг массивного объекта пропорционален массе M этого объекта:

Этому закону подчиняются искусственные спутники, планеты и астероиды, логично предположить, что этому закону должны подчиняться и звезды на краях спиральных галактик (Рис. 2).

Но в 1977 году наблюдатели Р. Талли и Дж. Фишер обнаружили закономерность M∝V4, которая связывает массу дисковой галактики M и скорость вращения V на ее краю. Зависимость M∝V4 выглядит противоречащей формуле (1), из которой следует, что M∝V2. Отметим, что на краю нашей галактики гравитационное ускорение крайне мало ~10-8 см/сек2, поэтому там могут действовать факторы, которые в условиях более сильных гравитационных полей не проявляются (на поверхности Земли гравитационное ускорение на 11 порядков больше).
Острое противоречие между соотношением Талли-Фишера и классическим законом Кеплера просто шокирует. Шок у израильского ученого Мордехая Милгрома оказался насколько силен, что он отказался от теории гравитации Ньютона-Эйнштейна и предложил модифицированную теорию тяготения (МОНД), где ввел феноменологический гравитационный потенциал на краю галактики, обеспечивающий строгое выполнение закона Талли-Фишера. В МОНД фигурирует новая постоянная - величина гравитационного ускорения 1.2*10-8 см/сек2. Вообще говоря, это классический случай теории ad hoc – то есть такой теории, которая не следует из каких-то фундаментальных законов, а введена специально для объяснения какого-то конкретного наблюдательного феномена.
Уточним, что загадка Талли-Фишера лежит отдельно от проблемы темной материи – ведь последняя введена для объяснения постоянной линейной скорости вращения галактик и не накладывает никаких ограничений на величину этой скорости на краю галактик.
Закон Талли-Фишера не является единственным таинственным феноменом в сложных отношениях галактических масс и скоростей. В 1976 году С. Фабер и Р. Джексон открыли похожую функцию M ∝ σ4 для эллиптических галактик (здесь σ – одномерная дисперсия скоростей). Поразительно, что эта загадочная четвертая степень от скорости появляется в таких разных системах, как плоские спиральные галактики, где звезды обращаются по почти круговым орбитам, и массивные эллиптические галактики, которые вращаются медленно, а звезды в них движутся по сильно вытянутым и наклонным траекториям.
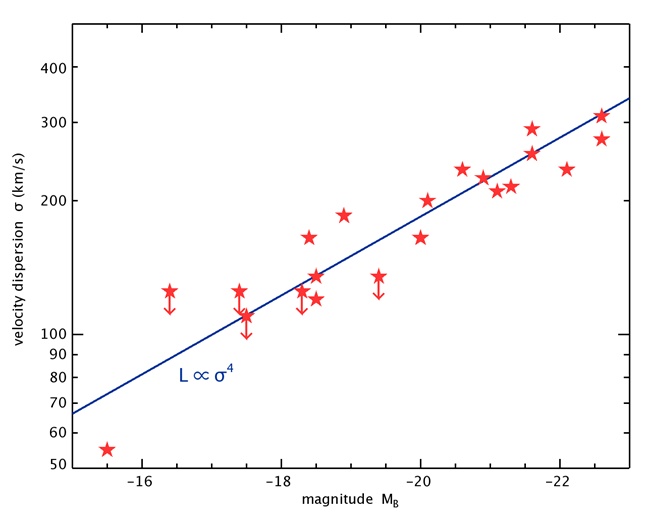
Дальше произошло что-то уже совсем невероятное: в 2000 году в работах Ferrarese & Merrit и Gebhardt и др. было установлено так называемое M-σ или «М-сигма» соотношение между сверхмассивными черными дырами (СМЧД) и дисперсией скоростей звезд в галактическом балдже (см. Рис. 2): M0∝σ4. Масса центральной СМЧД M0 обычно составляет малую часть (~ 0.1%) от массы балджа. Тем не менее, «М-сигма» соотношение означает тесную связь между столь небольшой относительной массой SMBH и таким глобальным параметром, как дисперсия звездных скоростей в балдже. (Отметим, что орбиты звезд в галактическом балдже имеют большой эксцентриситет, сопоставимый с эксцентриситетом орбит в эллиптических галактиках.)
Удивительное «М-сигма» соотношение оказалось в ряду аналогичных зависимостей Талли-Фишера и Фабера-Джексона. Очевидно, что во всех трех феноменах работает какой-то единый механизм, но как оказались связаны скорости кругового вращения на краю спиральных галактик, со скоростями звезд на эксцентриситетных орбитах в балджах и эллиптических галактик? И как компонента балджа в тысячу раз менее массивная, чем сам балдж, сумела повлиять на распределение скоростей в этом балдже? Многие десятки лет на эти острые вопросы не было ответов.
В последние годы стандартная теория иерархического и постепенного образования галактик, разработанная инфляционистами, была поставлена под сомнение наблюдателями (О.К. Сильченко, Происхождение и эволюция галактик, Век2, Фрязино, 2017). Появилась альтернативная теория, которая предполагает, что центральные сверхмассивные черные дыры образовались не после формирования галактик, а до них – и именно сверхмассивные дыры стали центром конденсации галактической материи (А.М. Черепащук, УФН, 184, 387, 2014). Эта концепция важности черных дыр в динамике Вселенной логично дополняется убедительной гипотезой о том, что темная материя состоит из многочисленных черных дыр звездных масс.
Покажем, что в этом сценарии (массивные черные дыры - первичны, галактики - вторичны) есть все возможности для решения загадки Талли-Фишера и других аналогичных соотношений.
Когда возраст расширяющейся Вселенной достиг 380 тысяч лет, протонно-электронная плазма охладилась до 3000 кельвинов и превратилась в нейтральный водород. Изотропность реликтового излучения, которое вырвалось в этот момент из прозрачной среды нейтрального водорода, показывает, что Вселенная в этот момент была очень однородна. Согласно новым воззрениям, в этой среде находилось какое-то количество сверхмассивных дыр, а также большое количество черных дыр звездных масс в роли темной материи.
В однородной среде из водорода и темной материи возникла гравитационная неустойчивость Джинса с длиной волны:
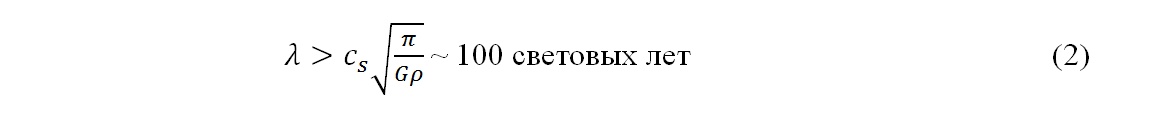
Массу образующегося облака Джинса можно оценить так (Зельдович и Новиков, 1975):

Гравитационное ускорение на границе такого облака Джинса с диаметром в 50 световых лет (т.е. равном области растущей плотности на полудлине волны колебаний) можно оценить как aj~GMj/r2 ~10-8 см/сек2. Вот тут в у каждого ученого (ну или просто хомо сапиенса) загорается красный сигнал тревоги: отчего во Вселенной, параметры которой меняются на десятки порядков, величина гравитационного ускорения на границе облаков Джинса (размер в сотню светолет) и на краю галактик (сто тысяч светолет) совпадает? Разница в размерах - в тысячу раз!
Когда вопрос правильно поставлен, то ответ найти несложно. Представим себе образование галактики вокруг сверхмассивной черной дыры, которая захватывает неосторожно приблизившиеся облака Джинса, разрывает их и строит вокруг себя галактический диск (или эллипсоид). Этот диск растет, растет, пока не достигает такого размера, что газ (или звезды) на его краю начинаются притягиваться к центру галактики так слабо, что ускорение притяжения достигает величины 10-8 см/сек2. А ведь вокруг юной галактики продолжают плавать многочисленные облака Джинса, которые постепенно превращаются в шаровые скопления из черных дыр и звезд. Эти шаровые скопления возмущают на уровне ~10-8 см/сек2 звезды на краю галактики, загоняя их вглубь или насовсем отрывая их. Тем самым, гравитационные возмущения от облаков Джинса ограничивают R - радиус галактики с массой M условием:

В небесной механике эта область называется "сферой тяготения". Теперь сделаем простое математическое упражнение (вы можете сделать это сами!): получим из уравнения (4) выражение для радиуса R∝M1/2 и подставим в формулу (1). Возведя получившее выражение в квадрат, получим закон Талли-Фишера в аналитическом виде (N. Gorkavyi, Galaxies, 10: 73, https://doi.org/10.3390/galaxies10030073, 2022):

Соотношение (5) поразительно просто и логично объясняет знаменитую загадочную зависимость Талли-Фишера между массой галактик и периферийной скоростью их вращения.
Наши рассуждения относятся к ранней Вселенной. Будет ли ограничение (4) работать в современную эпоху? Конечно, ведь облака Джинса до сих пор никуда не делись, они представляют собой стабильные кластеры из черных дыр и звезд. Эти кластеры постепенно были захвачены в гало галактик, где и движутся по эксцентриситетным и сильно наклоненным орбитам (отметим, что скопление Омега Центавра движется по ретроградной орбите – то есть вращается вокруг центра галактики в направлении противоположном вращению галактического диска). Гравитационные параметры этих древних облаков мало изменились – и они по-прежнему ограничивают размеры галактик условием (4). Шаровые скопления как пираньи, откусывают от края галактик звезды, чья гравитационная связь с основной галактикой ослабла.
Аналогичная логика работает и для эллиптических галактик: по какой бы орбите не двигалась звезда, выходя на край галактики, она испытывает возмущения от шаровых скоплений и подчиняется условию (4). Отличие только в том, что для вычисления скорости движения тел в эллиптических галактиках нужно использовать не условие кругового движения (1), а теорему вириала для одномерной дисперсии скоростей, что дает аналитическое выражение для закона Фабера-Джексона:

Рассмотрим происхождение соотношения «М-сигма». Из условия (4) следует, что площадь галактического диска пропорциональна его массе: πR2∝M. Аккреционный рост галактики (и ее балджа) прямо зависит от площади ее диска, а, следовательно, и от ее массы:

Уравнение (7) приводит к экспоненциальному закону роста галактики M=M0exp(γt), где γ – инкремент роста. Отметим, что площадь начального аккреционного диска прямо зависела от размера (или массы) черной дыры, выступившей затравкой для образования галактики. Следовательно, под массой M0 мы можем понимать массу начальной черной дыры (может быть, с каким-то коэффициентом). Учитывая уравнение (6), мы получаем обоснование «М-сигма» соотношения: связи массы SMBH M0 и одномерной дисперсии хаотических скоростей σ в балдже:

Таким образом, труднообъяснимая «М-сигма» зависимость легко получилась для модели Вселенной с популяцией реликтовых сверхмассивных черных дыр. Соотношение «M-сигма» можно считать прямым следствием и подтверждением аккреционной теории образования галактик вокруг сверхмассивных черных дыр (Рис.4).
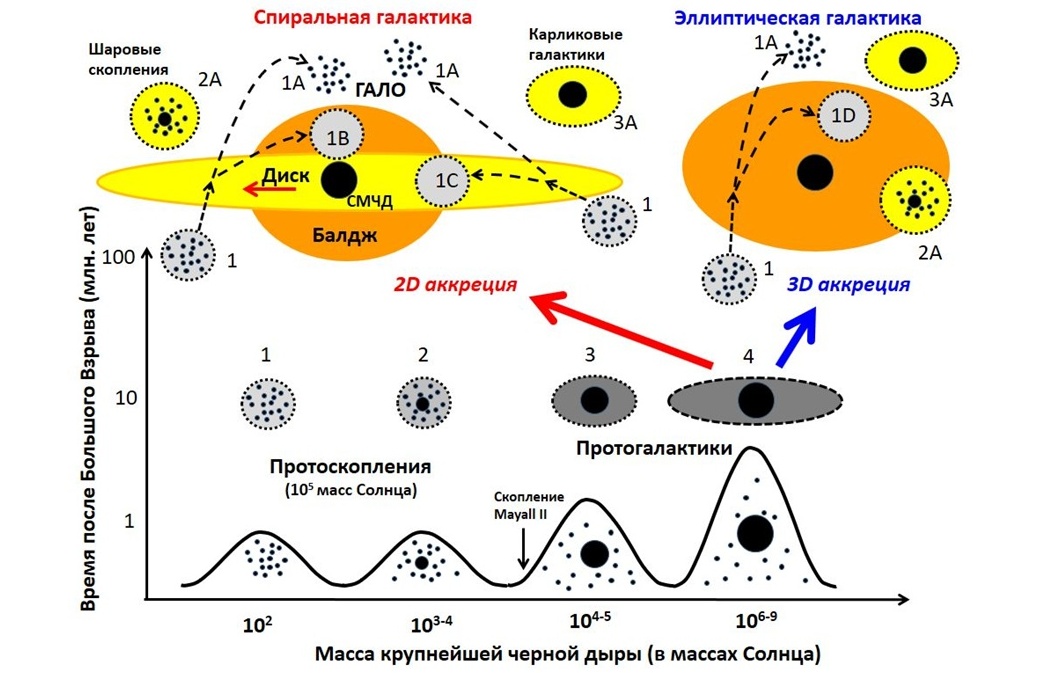
В распределении черных дыр по размерам есть не только черные дыры звездных масс (<100 масс Солнца) и сверхмассивные дыры (> 100 тысяч солнечных масс), но и какое-то количество черных дыр промежуточной массы. Когда в ранней Вселенной формировалось огромное количество облаков Джинса, то в них входили в основном черные дыры звездных масс. Но некоторым скоплениям повезло – и в них попали черные дыры промежуточной массы. Такая дыра в одиночку обладает большей возможностью для захвата газа, чем все остальные мелкие дыры шарового скопления. Именно этот газ, захваченный черной дырой промежуточной массы, коллапсирует в светила, которые превращают темное облако Джинса в сияющее шаровое звездное скопление (Рис. 4).
Предположение о том, что все шаровые скопления должны иметь в середине черную дыру промежуточной массы, сначала подтвердилось на примере звездного скопления Mayall II возле галактики Туманность Андромеды, которое обладает массой в 10 миллионов масс Солнца и центральной черной дырой массой в двадцать тысяч солнечных масс. Скопление Омега Центавра с центральной дырой в 8200 масс Солнца расположено в нашей Галактике и служит еще одним важным подтверждением гипотезы о массивных дырах внутри шаровых скоплений звезд.
Подведем итоги вышесказанному: шаровые скопления являются самыми древними коллективными структурами Вселенной, возникшими раньше галактик. Взаимодействуя со сверхмассивными дырами, скопления активно участвуют в росте спиральных и эллиптических галактик. Гравитационные возмущения от шаровых скоплений ограничивают периферийную скорость и размеры галактик, приводя к зависимостям типа Талли-Фишера. Шаровые скопления образованы черными дырами звездных масс и практически невидимы, составляя темную материю - основную часть массы Вселенной (https://elementy.ru//novosti_nauki/434235/Gipoteza_o_tsiklicheskoy_Vselennoy_poluchila_nablyudatelnuyu_podderzhku). Если в скоплении находится черная дыра промежуточной массы, то газ, захваченный этой дырой, превращает темное скопление в шаровое звездное скопление. Массы газа, захваченные сверхмассивными черными дырами, образуют более масштабные звездные структуры - галактики.
Процесс возникновения наблюдаемого распределения черных дыр, а также причины, по которым возле одних черных дыр образуются спиральные дисковые галактики, а возле других – эллиптические галактики, описаны в книге автора «Пульсирующая Вселенная» («Питер», 2024, 2-е издание).
https://www.piter.com/collection/new/product/pulsiruyuschaya-vselennaya
https://www.ozon.ru/product/pulsiruyushchaya-vselennaya-gorkavyy-nikolay-nikolaevich-1615984186/
https://global.wildberries.ru/product/pulsiruyushhaya-vselennaya-241693344?option=379702500
Автор: Gorkavyi






