Когда студент устраивается на работу в электронную компанию, очень здорово, если он уже умеет строить одну и ту же электронную схему разными способами, в зависимости от требований пропускной способности, максимальной тактовой частоты, размера и энергопотребления.
Как натренировать такое умение? Для новых домашних работ в программе Школы Синтеза Цифровых Схем мы решили разодрать на блоки реальный процессор и дать студентам задачу собирать разные специализированные вычислительные устройства из этих блоков, примерно как герои фильма "Безумный Макс: Дорога ярости" собирали свои боевые драндулеты из частей реальных автомобилей.
В качестве первой жертвы мы выбрали открытый RISC-V процессор Wally, полное описание которого будет в книге RISC-V Microprocessor System-On-Chip Design, by David Harris, James Stine, Sarah Harris, Rose Thompson, которая выходит в следущем году.
Нам не нужно ждать выхода книги, так как исходный код Wally уже есть на гитхабе. Технология такая: мы клонируем репо Wally рядом с репо домашних работ systemverilog-homework, оборачиваем блок работы с числами с плавающей точкой (FPU - Floating Point Unit) в наши собственные врапперы, после чего даем студентам серию заданий построить вычислители фиксированных функций из этих блоков.
Общая микроархитектурная диаграмма конвейера Wally. Интересующая нас сейчас часть - execution units в квадратике FPU:
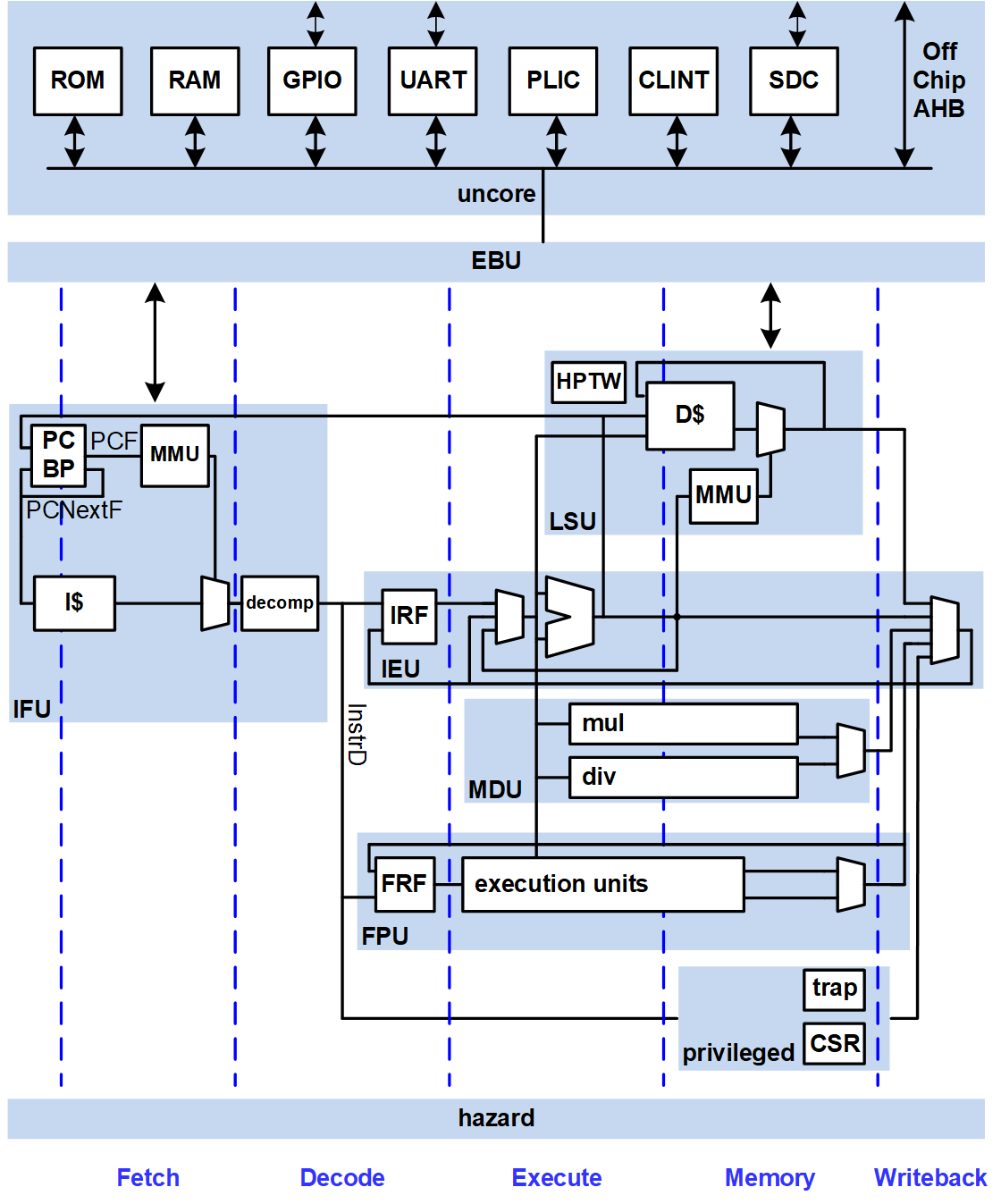
Арифметические строительные блоки которые получились оборачиванием FPU
Все блоки используют аргументы в формате IEEE 754 FP64 - то есть числа с плавающей точкой двойной точности (64 бита). При этом:
-
f_add, f_sub и f_mult - сложение, вычитание и умножение - имеют латентность два такта и являются конвейерными, то есть новую пару аргументов можено подавать на вход блока каждый такт (back-to-back), не дожидаясь завершения обработки предыдущей пары.
-
f_div и f_sqrt - деление и извлечение квадратного корня - переменная латентность в зависимости от значений аргументов - максимальную латентность нужно проверить.
-
f_less_or_equal - комбинационный блок для сравнения.
Примеры функций для реализации
-
Сортировка нескольких чисел.
-
Вычисление корней квадратного уравнения.
-
Вычисление рядов Маклорена (для синуса, экспоненты итд).
-
Преобразования координат для компьютерной графики, например перспективная проекция.
-
Алгоритм Томасуло - классический способ реализаций внеочередных вычислений в суперскалярном процессоре с набором арифметических блоков с разной латентностью.
Текущие задания в рамках Домашней работы номер 3
В Домашней работе номер 3 такие упражнения только начинаются. В нее мы включили:
-
Сортировку трех чисел с помощью трех блоков f_less_or_equal - комбинационная реализация - 03_06_sort_floats.
-
Сортировку трех чисел с помощью одного блока f_less_or_equal, обращения к которому сериализуются конечным автоматом - 03_07_sort_floats_using_fsm.
-
Вычисление дискриминанта квадратного уроавнения - реализация как вам угодно - 03_08_float_discriminant.
На что нужно обратить внимание при работе с числами с плавающей точкой
Домашние работы 3 и 4 в Школе Синтеза Цифровых Схем не ставят целью познакомить студента со всеми нюансами реализации операций с плавающей точкой. Вы будете использовать блоки как "черные ящики". Но для общего развития стоит погуглить какие-нибудь статьи про стандарт IEEE 754 и обратить внимание на следущие моменты:
-
В упражнениях мы используем числа двойной точности размером 64 бита - Double-precision floating-point format, который также называют FP64 or float64. Почему не 32-битный? Читатель может высказать предположение, что мы это сделали, чтобы жизнь медом не казалась в смысле тайминга внутри такта (static timing analysis - STA). Но причина гораздо банальнее: для упражнений мы используем Icarus Verilog, и в его текущей версии 12.0 есть дефект - он поддерживает функции $bitstoreal и $realtobits для типа real (FP64) и не поддерживает функции $bitstoshortreal и $shortrealtobits для типа shortreal (FP32). Мы используем эти функции в тестбенчах чтобы проверить дизайн студента.
-
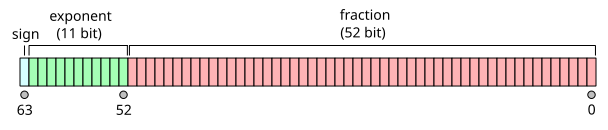
Посмотрите на формат числа - знак, порядок и мантисса. Обратите внимание, что в стандарте IEEE 754 есть положительный нуль и отрицательный нуль, причем их сравнение должно давать 1 (истина), хотя биты представления отличаются.
-
В стандарта IEEE 754 есть представления для бесконечностей (положительной и отрицательной - positive and negative infinity ) и для нечисел (Not a Number - NaN). Текущий код процессора Wally их не различает, хотя во многих других процессорах это разные сущности. Про это стоит почитать.
-
Также бывают quiet NaN and signaling NaN - это для наших упражнений нерелевантно, читать про это не нужно, но на будущее их стоит иметь в виду для других проектов процессоров.
-
Еще следует взять на заметку нормализованные и ненормализованные числа - если вы углубитесь в тему таких вычислений, эта сущность появится.
-
Почитайте про уже упомянутые $bitstoreal и $realtobits - и в стандарте, и в тестбенчах в домашке. Эти функции можно использовать не только для тестов, но и чтобы мониторить в логе всякие промежуточные значения вашего дизайна при отладке.
-
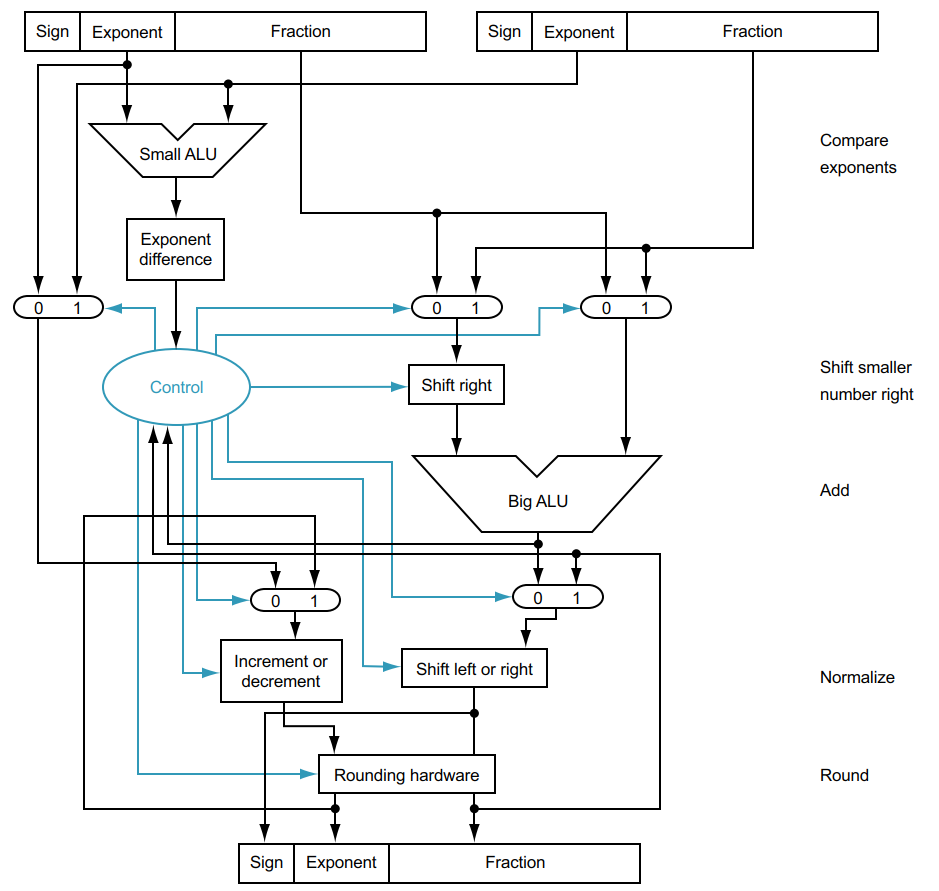
Вообще, как вы уже наверное догадались, арифметика с плавающей точкой нетривиальна, и даже простые сложения и умножения - это операции в несколько шагов, с деталями округления, нормализации итд. Посмотрите например на диаграмму блока сложения из книжки Паттерсона и Хеннесси ниже. В процессоре Wally, FPU которого мы используем на запчасти, сложения и умножения делаются литным блоком fused multiply-add с латентностью два такта. Но в процессорах, которые работают на более высокой тактовой частоте, такие блоки могут иметь латентность в несколько тактов.
Теперь кратко пройдемся по вариантам реализаций с точки зрения микроархитектуры.
Вариант микроархитектурной реализации 1 - Максимизируем пропускную способность
Если на размер схемы можно не обращать внимание, то стоит установить много блоков, для максимальной пропускной способности. Независимые операции выполнять параллельно; блоки для зависимых комбинационных или конвейерных операций ставить каскадом; если нужно выровнять аргументы по тактам, использовать сдвиговые регистры, кольцевые буферы или очереди FIFO. Если критический путь задержки сложной логики не вписывается в период тактового сигнала, разбивать его регистрами.
Блоки для параллельных операций. Пример из Домашней работы 4, но не из упражнений с плавающей точкой, а из упражнений с целочисленным квадратным корнем:
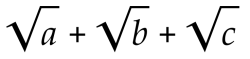
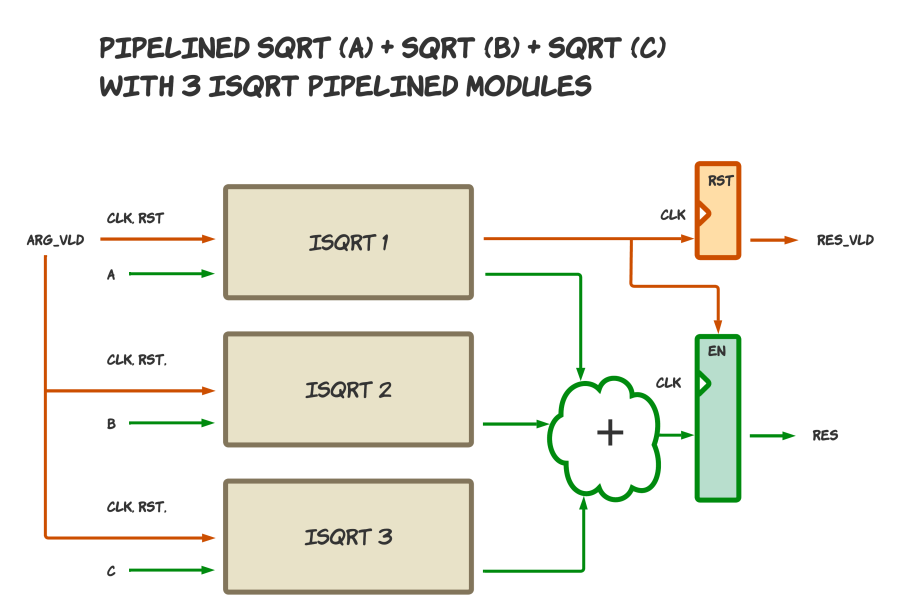
Организация вычислений для операций с зависимостями и выравниванием по времени с помощью очередей FIFO. Это тоже будет в Домашней работе 4:
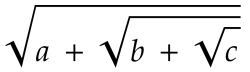
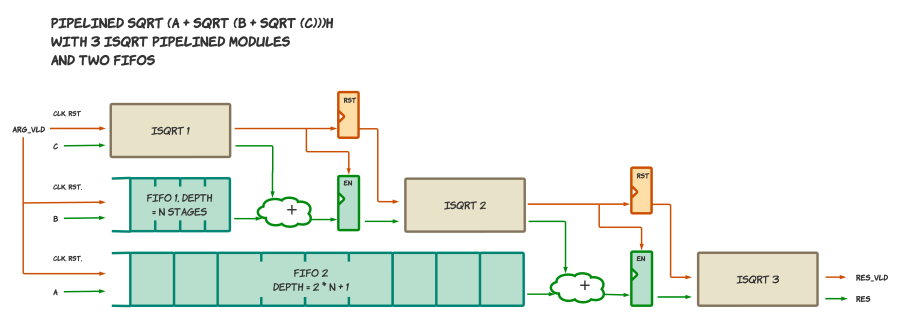
Вариант микроархитектурной реализации 2 - Минимизируем площадь и статическое энергопотребление
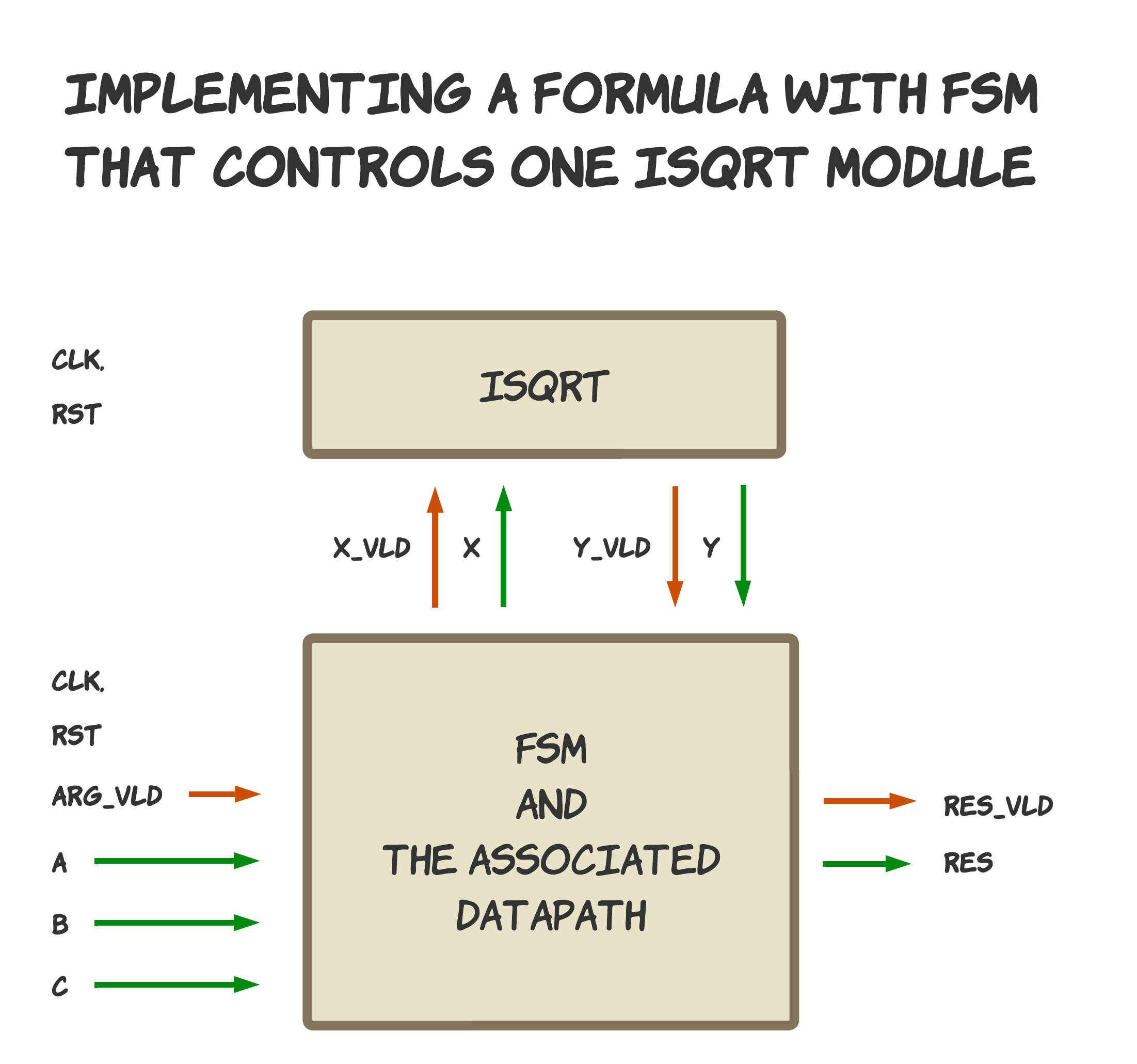
Если нужно экономить площадь на кристалле и связанное с нею статическое энергопотребление - то стоит установить по одному блоку на каждый тип операций (сложение, умножение итд) и использовать их повторно для разных частей формулы. Такое переиспользование можно сделать с помощью конечного автомата:
Пример из Домашней работы 3:
Вариант микроархитектурной реализации 3 - Добавляем контроль потока данных
Если за нашим модулем стоит другой модуль, который не всегда может принять результаты вычислений, то нам нужно контролировать поток данных с помощью дополнительного сигнала ready. Например вот так будет выглядеть интерфейс модуля который вычисляет корни квадратного уравнения:
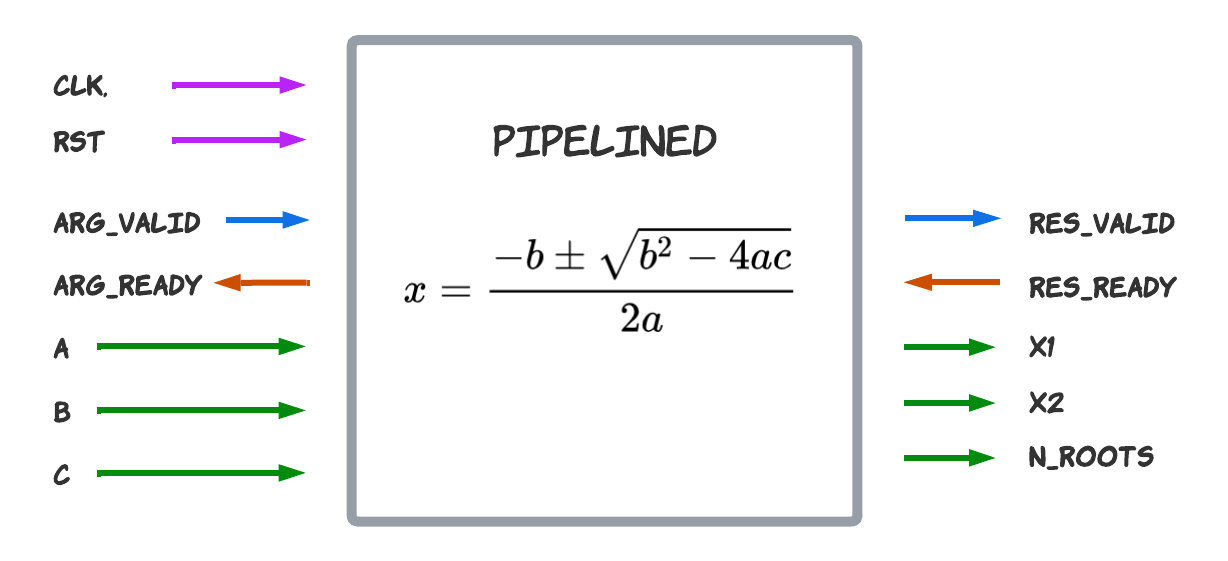
Внутри такой модуль можно реализовать разными способами. В старину было популярно строить конвейер с глобальной остановкой (global stall) или двойными буферами (double buffers), описанными в полезной книжке Digital Design: A Systems Approach by William James Dally and R. Curtis Harting.
Более современный способ - ставить после конвейера очередь FIFO, в которую сливать результаты, и вести учет данных идущих по конвейеру (transactions in flight - "в полете") c помощью кредитных счетчиков, как описано в Modern System-on-Chip Design by David J. Greaves, правда без примеров кода (но такие примеры есть у нас в репозитории basics-graphics-music).

Не только IEEE 754
В заключение добавим что уже несколько лет муссируются альтернативы IEEE 754 - Unum и Posit. Unum продвигает ученый из Калтеха John Gustafson, автор книги The End of Error, «Конец Ошибки». Posit — это версия Unum-а, которую можно более эффективно, чем Unum, реализовать в аппаратуре.

Пример реализации Posit описан в статье PERI: A Configurable Posit Enabled RISC-V Core. Вы тоже можете попробовать поупражняться с собственной конвейерной микроархитектурой такого вычислителя и максимизировать его тактовую частоту, используя для измерений статический анализ тайминга в открытом пакете OpenLane.
Мы надеемся что в результате выполнения домашних работ из Школы Синтеза Цифровых Схем вы получите набор инструментов для конструирования своих собственных суперкомпьютеров, больших и малых. Вы можете симулировать их в Verilator и Icarus Verilog, прототипировать на FPGA платах и синтезировать с помощью Open Lane. В МИЭТ год назад появился MPW сервис, так что лучшие студенты смогут наверное даже изготовить свои чипы на фабрике. Успехов!

Автор: YuriPanchul