Главная

Реалистичное гравитационное линзование на Unity

2014-09-05 в 6:48, admin, рубрики: shaders, unity3d, unity3d уроки

Эффект гравитационной линзы вызванный скоплением галактик RCS2 032727-132623

Возникла недавно необходимость реализовать на Unity достаточно правдоподобное изображение черной дыры и, соответственно, эффект гравитационного линзирования ею вызываемого. Первой мыслью было найти готовую реализацию и подстроить под себя, однако, поскольку ни одного достаточно хорошего решения так и не нашел (что весьма странно, зная насколько популярны игры на космическую тематику), решил реализовать эффект самостоятельно, а заодно и поделиться результатом с хабросообществом.

Для начала напишем скрипт который мы повесим на камеру, и который будет применять шейдер к выводимому на экран изображению.

Скрипт

using UnityEngine;

[ExecuteInEditMode]
public class Lens: MonoBehaviour {
	public Shader  shader;
	
	public float   ratio = 1;  	//Отношение высоты к длине экрана, для правильного отображения шейдера
	public float   radius = 0; 	//Радиус черной дыры измеряемый в тех же единицах, что и остальные объекты на сцене

	public GUIText txt;

	public GameObject BH;  //Объект, позиция которого берется за позицию черной дыры

	private Material _material; //Материал на котором будет находится шейдер
	protected Material material {
		get {
			if (_material == null) {
				_material = new Material (shader);
				_material.hideFlags = HideFlags.HideAndDontSave;
			}
			return _material;
		} 
	}

	protected virtual void OnDisable() {
		if( _material ) {
			DestroyImmediate( _material );
		}
	}

	void OnRenderImage (RenderTexture source, RenderTexture destination) {
		if (shader && material) {
			//Находим позицию черной дыры в экранных координатах
			Vector2 pos = new Vector2(
				this.camera.WorldToScreenPoint (BH.transform.position).x / this.camera.pixelWidth,
				1-this.camera.WorldToScreenPoint (BH.transform.position).y / this.camera.pixelHeight);

			//Устанавливаем все необходимые для шейдера параметры
			material.SetVector("_Position", new Vector2(pos.x, pos.y));
			material.SetFloat("_Ratio", ratio);
			material.SetFloat("_Rad", radius);
			material.SetFloat("_Distance", Vector3.Distance(BH.transform.position, this.transform.position));
			//И применяем к полученному изображению.
			Graphics.Blit(source, destination, material);
		}
	}
}

Теперь приступим к более важной части: написанию самого шейдера.

Первым делом, нам необходимо получить радиус, в зависимости от которого будем искажать изображение:

float2 offset = i.uv - _Position; //Сдвигаем наш пиксель на нужную позицию
float2 ratio = {_Ratio,1}; //определяем соотношение сторон экрана
float rad = length(offset / ratio); //определяем расстояние

В физике, формула приломления луча света проходящего на расстоянии r от объекта с массой M имеет вид:

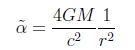
Для нас M — масса черной дыры. Зная, что радиус черной дыры определяется как

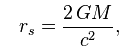
Получаем следующую конструкцию

float deformation = 2*_Rad*1/pow(rad*z,2);

где deformation — сила искажения в каждой конкретной точке, при этом z — некоторая зависимость размера искажения от расстояния на котором находится камера. Что бы понять как эта зависимость выражается, обратимся к формуле кольца Эйнштейна.

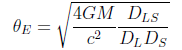
Где

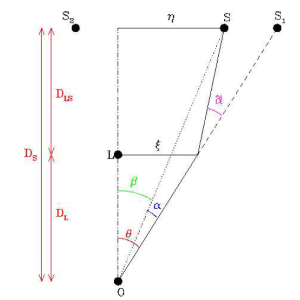
В данной формуле нас интересует ее зависимость от дистанции, потому, большую ее часть можно отбросить наблюдая лишь за

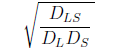
Поскольку шейдер обрабатывает 2х мерное изображение, мы не можем сказать о том, как далеко находятся объекты. И хотя это можно реализовать с помощью карты глубины, исказить их корректно не получиться, так как потребуются изображения всего что находиться за каждым из объектов. Поэтому предположим, что D_L<<D_S и D_L<<D_LS. Тогда мы видим, что размер искажения обратно пропорционален корню растояния, получаем

deformation = 2*_Rad*1/pow(rad*pow(_Distance,0.5),2);

Теперь применим нашу деформацию:

offset =offset*(1-deformation);

Вернем изображение на место и отобразим.

offset += _Position;

half4 res = tex2D(_MainTex, offset);
return res;

Полный код шейдера

Shader "Gravitation Lensing Shader" {
Properties {
	_MainTex ("Base (RGB)", 2D) = "white" {}
}

SubShader {
	Pass {
		ZTest Always Cull Off ZWrite Off
		Fog { Mode off }
				
		CGPROGRAM
		#pragma vertex vert
		#pragma fragment frag
		#pragma fragmentoption ARB_precision_hint_fastest 
		#include "UnityCG.cginc"

		uniform sampler2D _MainTex;
		uniform float2 _Position;
		uniform float _Rad;
		uniform float _Ratio;
		uniform float _Distance;

		struct v2f {
			float4 pos : POSITION;
			float2 uv : TEXCOORD0;
		};

		v2f vert( appdata_img v )
		{
			v2f o;
			o.pos = mul (UNITY_MATRIX_MVP, v.vertex);
			o.uv = v.texcoord;
			return o;
		}
		
		float4 frag (v2f i) : COLOR
		{
			float2 offset = i.uv - _Position; //Сдвигаем наш пиксель на нужную позицию
			float2 ratio = {_Ratio,1}; //определяем соотношение сторон экрана
			float rad = length(offset / ratio); //определяем расстояние от условного "центра" экрана.

			float deformation = 1/pow(rad*pow(_Distance,0.5),2)*_Rad*2;
			
			offset =offset*(1-deformation);
			
			offset += _Position;
			
			half4 res = tex2D(_MainTex, offset);
			//if (rad*_Distance<pow(2*_Rad/_Distance,0.5)*_Distance) {res.g+=0.2;} // проверка соблюдения радиуса эйнштейна
			//if (rad*_Distance<_Rad){res.r=0;res.g=0;res.b=0;} //проверка радиуса ЧД
			return res;
		}
		ENDCG

	}
}

Fallback off

}

Вот и все! Можно насладится результатом:

Данный шейдер реализует искажение лишь для одного массивного объекта. Для отображения того, что находиться перед черной дырой я использовал еще одну камеру которая рисует поверх основной. И хотя такое решение нельзя назвать элегантным, оно неплохо работает в моем случае.

Автор:

Источник