Карты из шестиугольников в Unity: части 1-3

От переводчика: эта статья — первая из подробной (27 частей) серии туториалов о создании карт из шестиугольников. Вот, что должно получиться в самом конце туториалов.

Часть1: создание сетки из шестиугольников

Оглавление

• Преобразуем квадраты в шестиугольники.
• Триангулируем сетку из шестиугольников.
• Работаем с кубическими координатами.
• Взаимодействуем с ячейками сетки.
• Создаём внутриигровой редактор.

Этот туториал является началом серии о картах из шестиугольников. Сетки из шестиугольников используются во многих играх, особенно в стратегиях, в том числе в Age of Wonders 3, Civilization 5 и Endless Legend. Мы начнём с основ, будем постепенно добавлять новые возможности и в результате создадим сложный рельеф на основе шестиугольников.

В этом туториале предполагается, что вы уже изучили серию Mesh Basics, которая начинается с Procedural Grid. Она была создана на Unity 5.3.1. В серии используются несколько версий Unity. Последняя часть сделана на Unity 2017.3.0p3.

Простая карта из шестиугольников.

О шестиугольниках

Зачем нужны шестиугольники? Если нам требуется сетка, то логично использовать квадраты. Квадраты и в самом деле просто отрисовывать и позиционировать, но у них есть и недостаток. Посмотрите на отдельный квадрат сетки, а потом на его соседей.

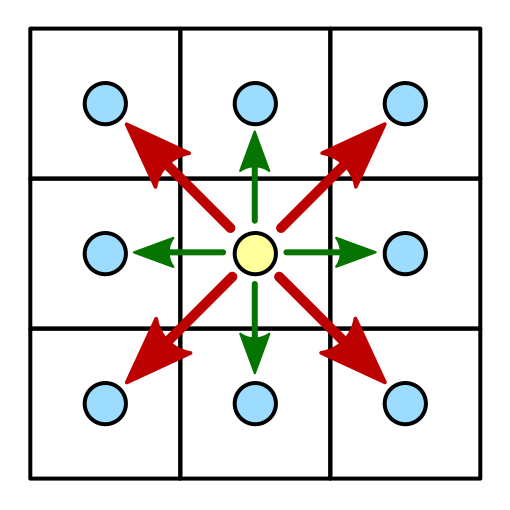
Квадрат и его соседи.

Всего у квадрата есть восемь соседей. Четырёх из них можно достичь, перейдя через ребро квадрата. Это горизонтальные и вертикальные соседи. Других четырёх можно достичь, перейдя через угол квадрата. Это диагональные соседи.

Каково расстояние между центрами соседних квадратных ячеек сетки? Если длина ребра равна 1, то для горизонтальных и вертикальных соседей ответ равен 1. Но для диагональных соседей ответ равен √2.

Различие между двумя видами соседей приводит к сложностям. Если мы используем дискретное движение, то как воспринимать перемещение по диагонали? Разрешать ли его вообще? Как сделать внешний вид более органичным? В разных играх используются различные подходы со своими преимуществами и недостатками. Один из подходов — не использовать квадратную сетку вообще, а вместо неё применять шестиугольники.

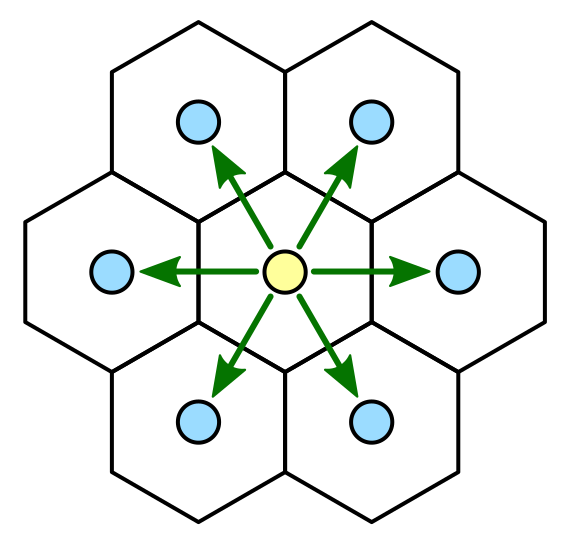
Шестиугольник и его соседи.

В отличие от квадрата, у шестиугольника не восемь, а шесть соседей. Все эти соседи являются соседними по рёбрам, угловых соседей нет. То есть есть только один тип соседей, что упрощает многое. Разумеется, сетку из шестиугольников сложнее построить, чем квадратную, но мы с этим справимся.

Прежде чем приступить к работе, нам нужно определиться с размером шестиугольников. Пусть длина ребра будет равна 10 единицам. Поскольку шестиугольник состоит из круга из шести равносторонних треугольников, то расстояние от центра до любого угла тоже равно 10. Эта величина определяет внешний радиус шестиугольной ячейки.

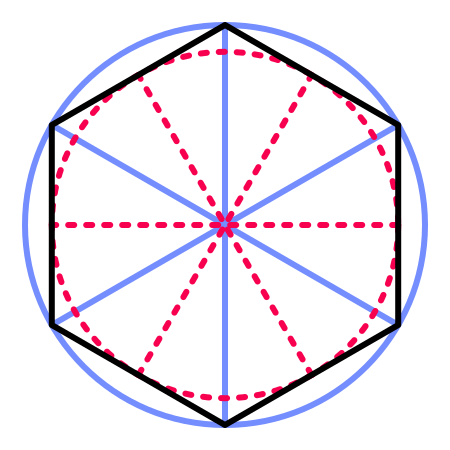
Внешний и внутренний радиус шестиугольника.

Также существует и внутренний радиус, который является расстоянием от центра до каждого из рёбер. Этот параметр важен, потому что расстояние между центрами соседей равно этому значению, умноженному на два. Внутренний радиус равен от внешнего радиуса, то есть в нашем случае . Давайте для удобства поместим эти параметры в статический класс.

using UnityEngine;

public static class HexMetrics {

	public const float outerRadius = 10f;

	public const float innerRadius = outerRadius * 0.866025404f;
}

Если уж мы этим занялись, то давайте определим позиции шести углов относительно центра ячейки. Следует учесть, что существует два способа ориентирования шестиугольника: вверх острой или плоской стороной. Мы поместим вверх угол. Начнём с этого угла и будем добавлять остальные по часовой стрелке. Поместим их на плоскость XZ, чтобы шестиугольники были лежали на земле.

Возможные ориентации.

	public static Vector3[] corners = {
		new Vector3(0f, 0f, outerRadius),
		new Vector3(innerRadius, 0f, 0.5f * outerRadius),
		new Vector3(innerRadius, 0f, -0.5f * outerRadius),
		new Vector3(0f, 0f, -outerRadius),
		new Vector3(-innerRadius, 0f, -0.5f * outerRadius),
		new Vector3(-innerRadius, 0f, 0.5f * outerRadius)
	};

unitypackage

Построение сетки

Для построения сетки из шестиугольников нам нужны ячейки сетки. Для этой цели создадим компонент HexCell. Пока оставим его пустым, потому что мы ещё не используем никаких данных ячеек.

using UnityEngine;

public class HexCell : MonoBehaviour {
}

Чтобы начать с самого простого, создадим объект-плоскость по умолчанию, добавим к нему компонент ячейки и превратим всё это в префаб.

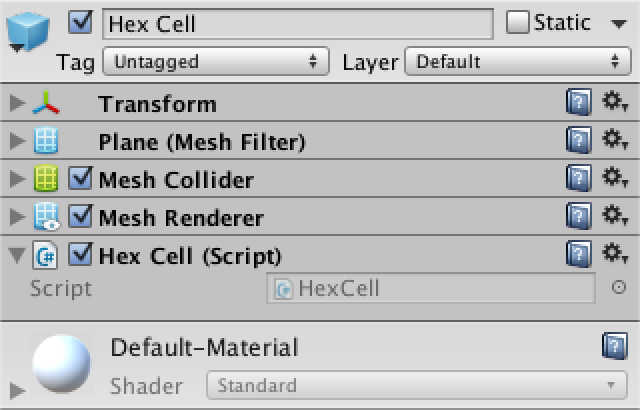
Использование плоскости в качестве префаба шестиугольной ячейки.

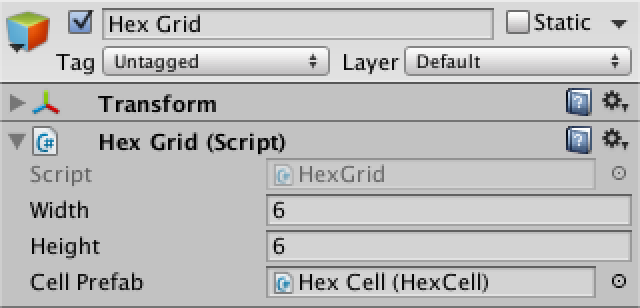
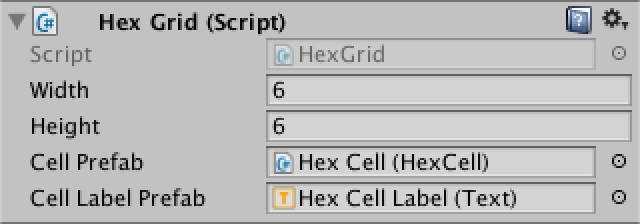
Теперь займёмся сеткой. Создадим простой компонент с общими переменными ширины, высоты и префаба ячейки. Затем добавим в сцену игровой объект с этим компонентом.

using UnityEngine;

public class HexGrid : MonoBehaviour {

	public int width = 6;
	public int height = 6;

	public HexCell cellPrefab;

}

Объект сетки из шестиугольников.

Давайте начнём с создания обычной сетки квадратов, потому что мы уже знаем, как это делается. Сохраним ячейки в массив, чтобы иметь возможность получать к ним доступ.

Поскольку плоскости по умолчанию имеют размер 10 на 10 единиц, то сместим каждую ячейку на эту величину.

	HexCell[] cells;

	void Awake () {
		cells = new HexCell[height * width];

		for (int z = 0, i = 0; z < height; z++) {
			for (int x = 0; x < width; x++) {
				CreateCell(x, z, i++);
			}
		}
	}
	
	void CreateCell (int x, int z, int i) {
		Vector3 position;
		position.x = x * 10f;
		position.y = 0f;
		position.z = z * 10f;

		HexCell cell = cells[i] = Instantiate<HexCell>(cellPrefab);
		cell.transform.SetParent(transform, false);
		cell.transform.localPosition = position;
	}

Квадратная сетка из плоскостей.

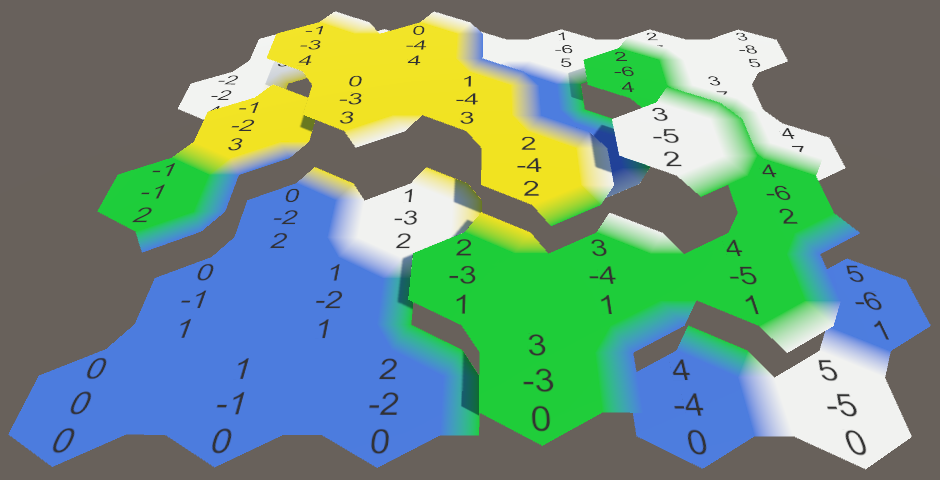
Так мы получили красивую сплошную сетку из квадратных ячеек. Но какая ячейка где находится? Разумеется, это легко проверить, но с шестиугольниками возникнут сложности. Было бы удобно, если бы мы одновременно могли видеть координаты всех ячеек.

Отображение координат

Добавим в сцену canvas, выбрав GameObject / UI / Canvas, и сделаем его дочерним элементом нашего объекта сетки. Так как этот canvas нужен только для информации, удалим его компонент raycaster. Также можно удалить объект event system, который автоматически был добавлен в сцену, потому что пока он нам не потребуется.

Выберите для Render Mode значение World Space и поверните на 90 градусов по оси X, чтобы canvas наложился на сетку. Задайте для pivot и для позиции значение zero. Придайте ему небольшое вертикальное смещение, чтобы его содержимое находилось наверху. Ширина и высота нам не важны, потому что мы располагаем содержимое самостоятельно. Мы можем присвоить значение 0, чтобы избавиться от большого прямоугольника в окне сцены.

В качестве финального штриха увеличим Dynamic Pixels Per Unit до 10. Так мы гарантируем, что текстовые объекты будут использовать достаточное разрешение текстур.

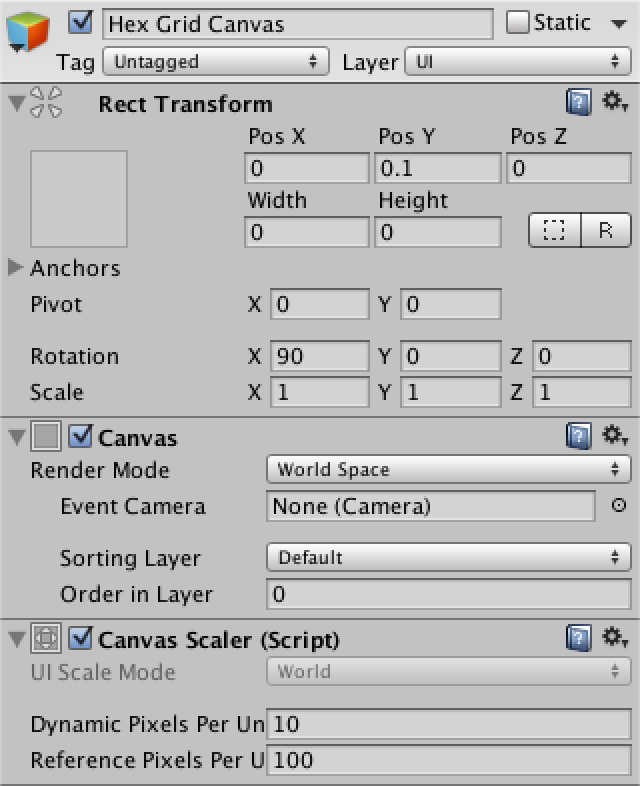
Canvas для координат сетки шестиугольников.

Для отображения координат создадим объект Text (GameObject / UI / Text) и превратим его в префаб. Отцентрируйте его anchors и pivot, задайте размер 5 на 15. Текст тоже должен быть горизонтально и вертикально выровнен по центру. Зададим размер шрифта 4. Наконец, мы не хотим использовать текст по умолчанию и не будем использовать Rich Text. Также нам не важно, включен ли Raycast Target, потому что для нашего canvas он всё равно не понадобится.

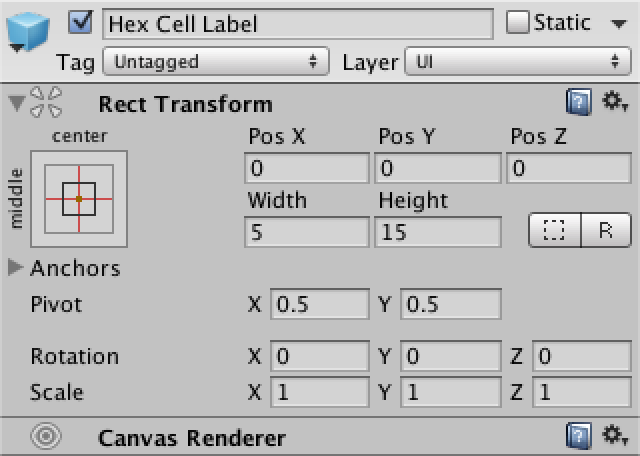
Префаб метки ячейки.

Теперь нам нужно сообщить сетке о canvas и префабе. Добавим в начало её скрипта using UnityEngine.UI;, чтобы удобно получить доступ к типу UnityEngine.UI.Text. Для префаба метки нужна общая переменная, а canvas можно найти вызовом GetComponentInChildren.

	public Text cellLabelPrefab;

	Canvas gridCanvas;

	void Awake () {
		gridCanvas = GetComponentInChildren<Canvas>();
		
		…
	}

Соединение префаба метки.

После подключения префаба метки мы можем создавать её экземпляры и отображать координаты ячейки. Между X и Z вставим символ новой строки, чтобы они оказались на отдельных строках.

	void CreateCell (int x, int z, int i) {
		…

		Text label = Instantiate<Text>(cellLabelPrefab);
		label.rectTransform.SetParent(gridCanvas.transform, false);
		label.rectTransform.anchoredPosition =
			new Vector2(position.x, position.z);
		label.text = x.ToString() + "n" + z.ToString();
	}

Отображение координат.

Позиции шестиугольников

Теперь, когда мы можем наглядно распознать каждую ячейку, давайте приступим к их перемещению. Мы знаем, что расстояние между соседними шестиугольными ячейками в направлении X равно удвоенному внутреннему радиусу. Мы этим воспользуемся. Кроме того, расстояние до следующей строки ячеек должно быть в 1,5 раза больше, чем внешний радиус.

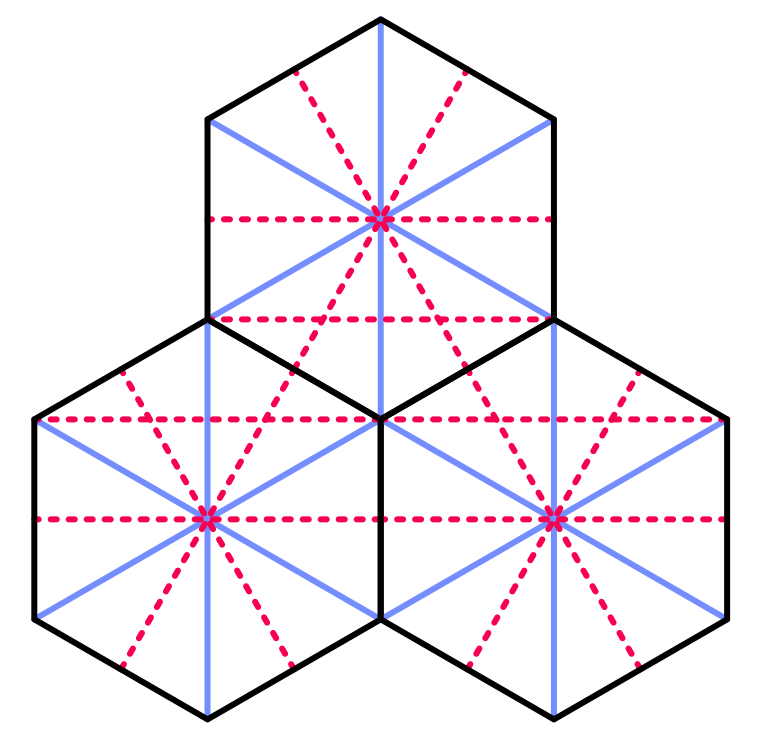
Геометрия соседних шестиугольников.

		position.x = x * (HexMetrics.innerRadius * 2f);
		position.y = 0f;
		position.z = z * (HexMetrics.outerRadius * 1.5f);

Применяем расстояния между шестиугольниками без смещений.

Разумеется, порядковые строки шестиугольников не расположены ровно одна над другой. Каждая строка смещена по оси X на величину внутреннего радиуса. Это значение можно получить, прибавив половину Z к X, а затем умножить на удвоенный внутренний радиус.

		position.x = (x + z * 0.5f) * (HexMetrics.innerRadius * 2f);

Правильное размещение шестиугольников создаёт сетку в виде ромба.

Хотя так мы разместили ячейки в правильные позиции шестиугольников, наша сетка теперь заполняет ромб, а не прямоугольник. Нам намного удобнее работать с прямоугольными сетками, поэтому давайте заставим ячейки вернуться обратно в строй. Это можно сделать, вернув назад часть смещения. В каждой второй строке все ячейки должны смещаться обратно на один дополнительный шаг. Для этого нам нужно перед умножением вычесть результат целочисленного деления Z на 2.

		position.x = (x + z * 0.5f - z / 2) * (HexMetrics.innerRadius * 2f);

Расположение шестиугольников в прямоугольной области.

unitypackage

Рендеринг шестиугольников

Правильно разместив ячейки, мы можем перейти к отображению настоящих шестиугольников. Сначала нам нужно избавиться от плоскостей, поэтому удалим из префаба ячейки все компоненты, кроме HexCell.

Плоскостей больше нет.

Как и в туториалах Mesh Basics, для рендеринга всей сетки мы используем один меш. Однако на этот раз мы не будем заранее задавать количество нужных вершин и треугольников. Вместо этого мы воспользуемся списками.

Создайте новый компонент HexMesh, который займётся нашим мешем. Для него потребуются mesh filter и renderer, у него есть меш и списки для вершин и треугольников.

using UnityEngine;
using System.Collections.Generic;

[RequireComponent(typeof(MeshFilter), typeof(MeshRenderer))]
public class HexMesh : MonoBehaviour {

	Mesh hexMesh;
	List<Vector3> vertices;
	List<int> triangles;

	void Awake () {
		GetComponent<MeshFilter>().mesh = hexMesh = new Mesh();
		hexMesh.name = "Hex Mesh";
		vertices = new List<Vector3>();
		triangles = new List<int>();
	}
}

Создадим для нашей сетки новый дочерний объект с этим компонентом. Он автоматически получит mesh renderer, но ему не будет назначен материал. Поэтому добавим к нему материал по умолчанию.

Объект Hex mesh.

Теперь HexGrid сможет получить его меш шестиугольников таким же образом, как он находил canvas.

	HexMesh hexMesh;

	void Awake () {
		gridCanvas = GetComponentInChildren<Canvas>();
		hexMesh = GetComponentInChildren<HexMesh>();
		
		…
	}

После Awake сетки она должна приказать мешу триангулировать его ячейки. Мы должны быть уверены, что это произойдёт после Awake компонента hex mesh. Так как Start вызывается позже, вставим соответствующий код туда.

	void Start () {
		hexMesh.Triangulate(cells);
	}

Этот метод HexMesh.Triangulate можно вызвать в любой момент времени, даже если ячейки уже триангулировались ранее. Поэтому нам стоит начать с очистки старых данных. При обходе в цикле по всем ячейкам мы триангулируем их по отдельности. Завершив эту операцию, назначим сгенерированные вершины и треугольники мешу, а закончим пересчётом нормалей меша.

	public void Triangulate (HexCell[] cells) {
		hexMesh.Clear();
		vertices.Clear();
		triangles.Clear();
		for (int i = 0; i < cells.Length; i++) {
			Triangulate(cells[i]);
		}
		hexMesh.vertices = vertices.ToArray();
		hexMesh.triangles = triangles.ToArray();
		hexMesh.RecalculateNormals();
	}
	
	void Triangulate (HexCell cell) {
	}

Так как шестиугольники составлены из треугольников, давайте создадим удобный метод для добавления треугольника на основе позиций трёх вершин. Он будет просто добавлять вершины по порядку. Также он добавить индексы этих вершин, чтобы сформировать треугольник. Индекс первой вершины равен длине списка вершин до добавления в него новых вершин. Не забывайте об этом при добавлении вершин.

	void AddTriangle (Vector3 v1, Vector3 v2, Vector3 v3) {
		int vertexIndex = vertices.Count;
		vertices.Add(v1);
		vertices.Add(v2);
		vertices.Add(v3);
		triangles.Add(vertexIndex);
		triangles.Add(vertexIndex + 1);
		triangles.Add(vertexIndex + 2);
	}

Теперь мы можем триангулировать наши ячейки. Давайте начнём с первого треугольника. Его первая вершина находится в центре шестиугольника. Двумя другими вершинами являются первый и второй углы относительно центра.

	void Triangulate (HexCell cell) {
		Vector3 center = cell.transform.localPosition;
		AddTriangle(
			center,
			center + HexMetrics.corners[0],
			center + HexMetrics.corners[1]
		);
	}

Первый треугольник каждой ячейки.

Это сработало, поэтому давайте обойдём в цикле все шесть треугольников.

		Vector3 center = cell.transform.localPosition;
		for (int i = 0; i < 6; i++) {
			AddTriangle(
				center,
				center + HexMetrics.corners[i],
				center + HexMetrics.corners[i + 1]
			);
		}

К сожалению, этот процесс приведёт к IndexOutOfRangeException. Так происходит потому, что последний треугольник пытается получить седьмой угол, которого не существует. Разумеется, он должен вернуться назад и использовать в качестве последней вершины первого угла. Или же мы можем дублировать первый угол в HexMetrics.corners, чтобы не выходить за границы.

	public static Vector3[] corners = {
		new Vector3(0f, 0f, outerRadius),
		new Vector3(innerRadius, 0f, 0.5f * outerRadius),
		new Vector3(innerRadius, 0f, -0.5f * outerRadius),
		new Vector3(0f, 0f, -outerRadius),
		new Vector3(-innerRadius, 0f, -0.5f * outerRadius),
		new Vector3(-innerRadius, 0f, 0.5f * outerRadius),
		new Vector3(0f, 0f, outerRadius)
	};

Шестиугольники полностью.

unitypackage

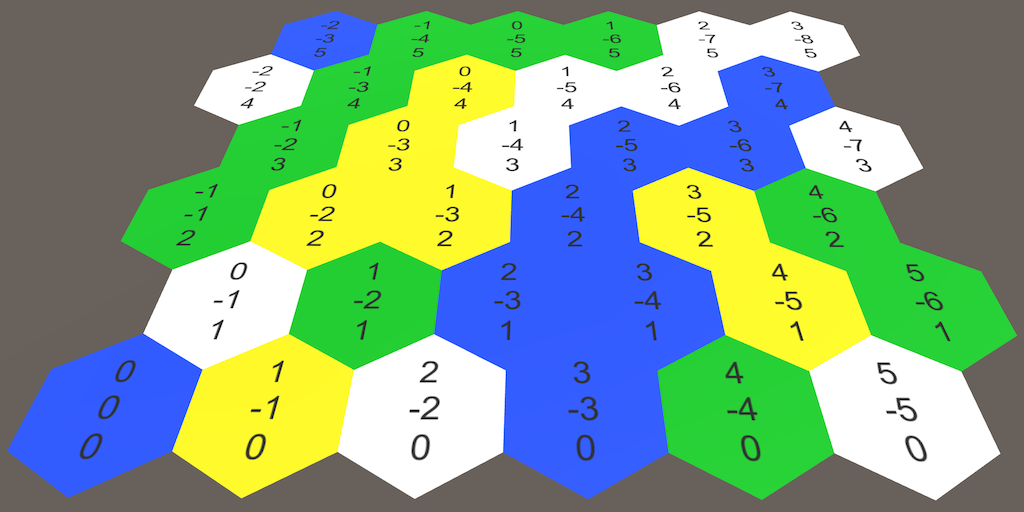
Шестиугольные координаты

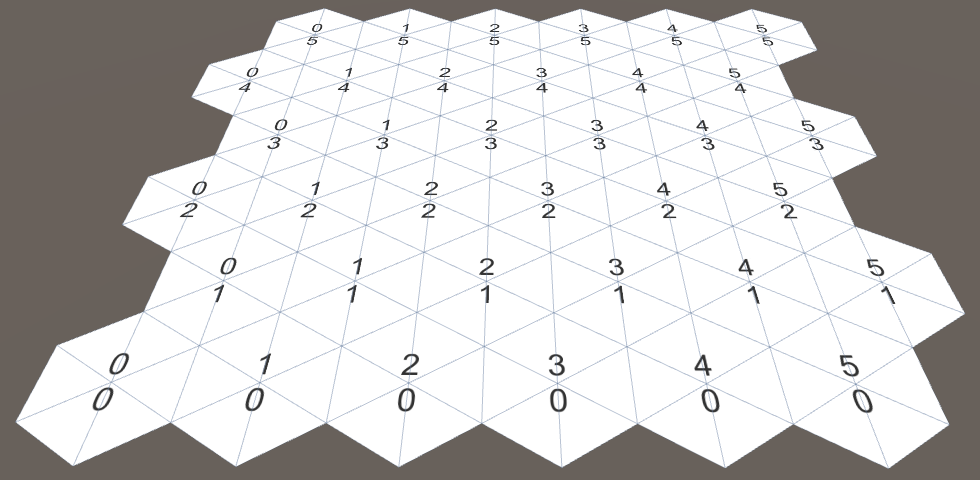
Давайте снова взглянем на координаты ячеек, теперь в контексте сетки шестиугольников. Координата Z выглядит нормально, а координата X двигается зигзагами. Это побочный эффект смещения строк для покрытия прямоугольной области.

Смещённые координаты с выделенными нулевыми строками.

При работе с шестиугольниками такие смещённые координаты обрабатывать непросто. Давайте добавим struct HexCoordinates, которую можно будет использовать для преобразования в другую систему координат. Сделаем её сериализуемой, чтобы Unity мог хранить её и она переживала рекомпиляцию в режиме Play. Также сделаем эти координаты immutable, воспользовавшись свойствами public readonly.

using UnityEngine;

[System.Serializable]
public struct HexCoordinates {

	public int X { get; private set; }

	public int Z { get; private set; }

	public HexCoordinates (int x, int z) {
		X = x;
		Z = z;
	}
}

Добавим статический метод для создания множества координат из обычных смещённых координат. Пока мы будем просто копировать эти координаты.

	public static HexCoordinates FromOffsetCoordinates (int x, int z) {
		return new HexCoordinates(x, z);
	}
}

Добавим также удобные методы преобразования строк. Метод ToString по умолчанию возвращает название типа struct, которое нам не очень полезно. Переопределим его, чтобы он возвращал координаты на одной строке. Также добавим метод для вывода координат на отдельные строки, потому что мы уже используем такую схему.

	public override string ToString () {
		return "(" + X.ToString() + ", " + Z.ToString() + ")";
	}

	public string ToStringOnSeparateLines () {
		return X.ToString() + "n" + Z.ToString();
	}

Теперь мы можем передать множество координат нашему компоненту HexCell.

public class HexCell : MonoBehaviour {

	public HexCoordinates coordinates;
}

Изменим HexGrid.CreateCell так, чтобы он мог воспользоваться новыми координатами.

		HexCell cell = cells[i] = Instantiate<HexCell>(cellPrefab);
		cell.transform.SetParent(transform, false);
		cell.transform.localPosition = position;
		cell.coordinates = HexCoordinates.FromOffsetCoordinates(x, z);
		
		Text label = Instantiate<Text>(cellLabelPrefab);
		label.rectTransform.SetParent(gridCanvas.transform, false);
		label.rectTransform.anchoredPosition =
			new Vector2(position.x, position.z);
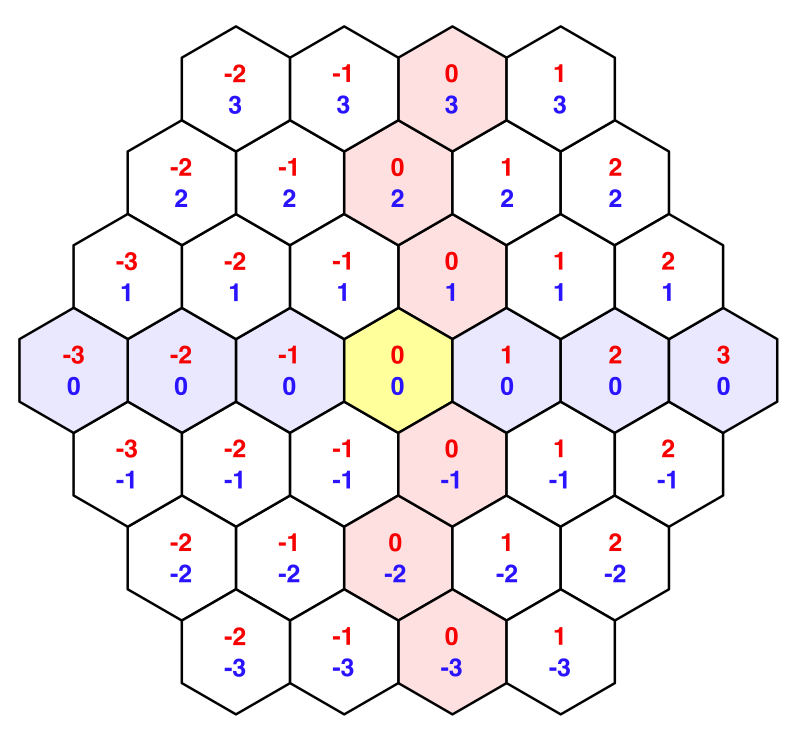
		label.text = cell.coordinates.ToStringOnSeparateLines();

Теперь давайте переделаем эти координаты X, чтобы они были выровнены вдоль прямой оси. Это можно сделать, отменив горизонтальный сдвиг. Получившийся результат обычно называют осевыми координатами.

	public static HexCoordinates FromOffsetCoordinates (int x, int z) {
		return new HexCoordinates(x - z / 2, z);
	}

Осевые координаты.

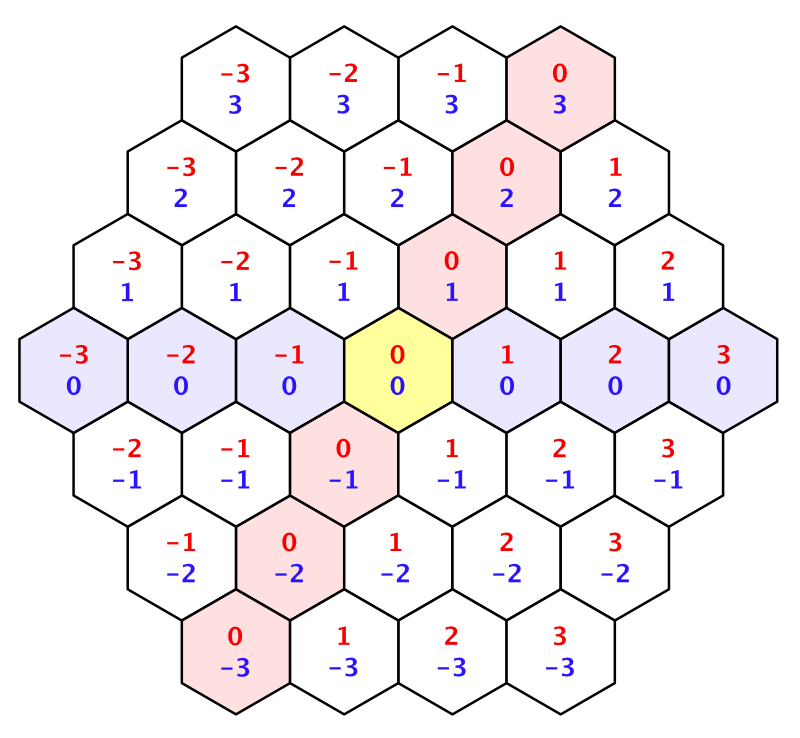
Эта двухмерная система координат позволяет нам последовательно описывать движение смещения в четырёх направлениях. Однако особого внимания по-прежнему требуют два оставшихся направления. Это даёт нам понять, что существует третье измерение. И в самом деле, еслы бы мы горизонтально перевернули измерение X, то получили бы недостающее измерение Y.

Появляется измерение Y.

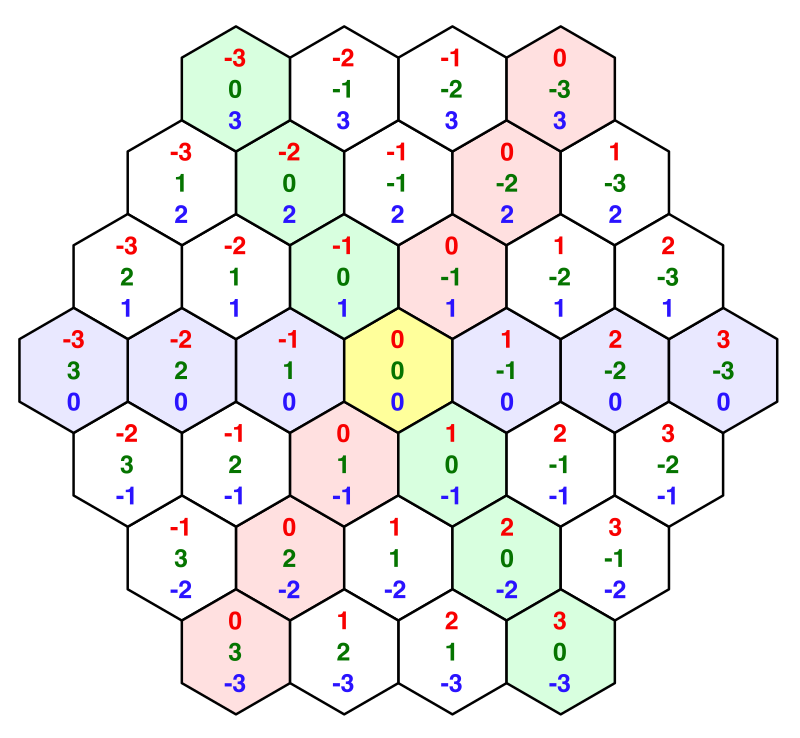
Так как эти измерения X и Y являются зеркальными копиями друг друга, сложение их координат всегда даёт одинаковый результат, если Z остаётся постоянным. На самом деле, если сложить все три координаты, то мы всегда будем получать ноль. Если увеличить одну координату, то придётся уменьшать другую. И в самом деле, это даёт нам шесть возможных направлений движения. Такие координаты обычно называются кубическими, потому что они трёхмерны, а топология напоминает куб.

Поскольку сумма всех координат равна нулю, мы всегда можем получить любую из координат из двух других. Так как мы уже храним координаты X и Z, то нам не нужно хранить координату Y.
Мы можем добавить свойство, вычисляющее её при необходимости и использовать его в строковых методах.

	public int Y {
		get {
			return -X - Z;
		}
	}

	public override string ToString () {
		return "(" +
			X.ToString() + ", " + Y.ToString() + ", " + Z.ToString() + ")";
	}

	public string ToStringOnSeparateLines () {
		return X.ToString() + "n" + Y.ToString() + "n" + Z.ToString();
	}

Кубические координаты.

Координаты в инспекторе

Выберите в режиме Play одну из ячеек сетки. Оказывается, что инспектор не отображает её координаты, показывается только метка префикса HexCell.coordinates.

Инспектор не отображает координаты.

Хотя большой проблемы в этом нет, было бы здорово отображать координаты. Unity не показывает координаты, потому что они не помечены как сериализуемые поля. Чтобы отобразить их, нужно явным образом задать сериализируемые поля для X и Z.

	[SerializeField]
	private int x, z;

	public int X {
		get {
			return x;
		}
	}

	public int Z {
		get {
			return z;
		}
	}

	public HexCoordinates (int x, int z) {
		this.x = x;
		this.z = z;
	}

Координаты X и Z пока не отображаются, но их можно изменять. Нам это не нужно, потому что координаты должны быть фиксированными. Также не очень хорошо, что они отображаются друг под другом.

Мы можем сделать лучше: определить собственный property drawer для типа HexCoordinates. Создадим скрипт HexCoordinatesDrawer и вставим его в папку Editor, потому что это скрипт только для редактора.

Класс должен расширять UnityEditor.PropertyDrawer и ему требуется атрибут UnityEditor.CustomPropertyDrawer, чтобы ассоциировать его с подходящим типом.

using UnityEngine;
using UnityEditor;

[CustomPropertyDrawer(typeof(HexCoordinates))]
public class HexCoordinatesDrawer : PropertyDrawer {
}

Property drawers отображают своё содержимое с помощью метода OnGUI. Этот метод позволил отрисовывать внутри экранного прямоугольника сериализуемые данные свойства и метку поля, к которой они принадлежат.

	public override void OnGUI (
		Rect position, SerializedProperty property, GUIContent label
	) {
	}

Извлечём из свойства значения x и z, а затем используем их для создания нового множества координат. Затем отрисуем в выбранной позиции метку GUI с помощью нашего метода HexCoordinates.ToString.

	public override void OnGUI (
		Rect position, SerializedProperty property, GUIContent label
	) {
		HexCoordinates coordinates = new HexCoordinates(
			property.FindPropertyRelative("x").intValue,
			property.FindPropertyRelative("z").intValue
		);
		
		GUI.Label(position, coordinates.ToString());
	}

Координаты без метки префикса.

Так мы отобразим координаты, но теперь нам не хватает имени поля. Эти имена обычно отрисовываются с помощью метода EditorGUI.PrefixLabel. В качестве бонуса он возвращает выровненный прямоугольник, который соответствует пространству справа от этой метки.

		position = EditorGUI.PrefixLabel(position, label);
		GUI.Label(position, coordinates.ToString());

Координаты с меткой.

unitypackage

Касаемся ячеек

Сетка из шестиугольников не очень интересна, если мы не можем с ней взаимодействовать. Простейшим взаимодействием будет касание ячейки, поэтому давайте добавим его поддержку. Пока мы просто вставим этот код непосредственно в HexGrid. Когда он начнёт работать, мы переместим его в другое место.

Чтобы коснуться ячейки, можно испускать в сцену лучи из позиции курсора мыши. Мы можем использовать тот же подход, что и в туториале Mesh Deformation.

	void Update () {
		if (Input.GetMouseButton(0)) {
			HandleInput();
		}
	}

	void HandleInput () {
		Ray inputRay = Camera.main.ScreenPointToRay(Input.mousePosition);
		RaycastHit hit;
		if (Physics.Raycast(inputRay, out hit)) {
			TouchCell(hit.point);
		}
	}
	
	void TouchCell (Vector3 position) {
		position = transform.InverseTransformPoint(position);
		Debug.Log("touched at " + position);
	}

Пока код ничего не делает. Нам нужно добавить к сетке коллайдер, чтобы луч мог с чем-нибудь столкнуться. Поэтому дадим HexMesh меш коллайдера.

	MeshCollider meshCollider;

	void Awake () {
		GetComponent<MeshFilter>().mesh = hexMesh = new Mesh();
		meshCollider = gameObject.AddComponent<MeshCollider>();
		…
	}

После завершения триангуляции назначим меш коллайдеру.

	public void Triangulate (HexCell[] cells) {
		…
		meshCollider.sharedMesh = hexMesh;
	}

Теперь мы можем касаться сетки! Но какой ячейки мы касаемся? Чтобы узнать это, нам нужно преобразовать позицию касания в координаты шестиугольников. Это работа для HexCoordinates, поэтому объявим, что у него есть статический метод FromPosition.

	public void TouchCell (Vector3 position) {
		position = transform.InverseTransformPoint(position);
		HexCoordinates coordinates = HexCoordinates.FromPosition(position);
		Debug.Log("touched at " + coordinates.ToString());
	}

Как этот метод будет определять, какая координата принадлежит позиции? Мы можем начать с того, что разделим x на горизонтальную ширину шестиугольника. А поскольку координата Y является зеркальным отражением координаты X, отрицательное значение x даёт нам y.

	public static HexCoordinates FromPosition (Vector3 position) {
		float x = position.x / (HexMetrics.innerRadius * 2f);
		float y = -x;
	}

Разумеется, это давало бы нам верные координаты, если бы Z была равна нулю. Мы снова должны выполнять сдвиг при движении вдоль Z. Через каждые две строки мы должны сдвигаться влево на всю единицу.

		float offset = position.z / (HexMetrics.outerRadius * 3f);
		x -= offset;
		y -= offset;

В результате наши значения x и y оказываются целыми числами в центре каждой ячейки. Поэтому округляя их до целых, мы должны получить координаты. Также мы вычисляем Z и таким образом получаем окончательные координаты.

		int iX = Mathf.RoundToInt(x);
		int iY = Mathf.RoundToInt(y);
		int iZ = Mathf.RoundToInt(-x -y);

		return new HexCoordinates(iX, iZ);

Результаты выглядят многообещающе, но верны ли эти координаты? При внимательном изучении можно обнаружить, что иногда у нас получаются координаты, сумма которых не равна нулю! Давайте включим уведомление, чтобы убедиться, что это действительно происходит.

		if (iX + iY + iZ != 0) {
			Debug.LogWarning("rounding error!");
		}
		
		return new HexCoordinates(iX, iZ);

Мы и в самом деле получаем уведомления. Как нам исправить эту ошибку? Она возникает только рядом с рёбрами между шестиугольниками. То есть проблемы вызывает округление координат. Какая из координат округляется в неверную сторону? Чем дальше мы отходим от центра ячейки, тем большее округление мы получаем. Поэтому логично предположить, что неверной является координата, округляемая больше всех.

Тогда решение заключается в том, чтобы отбрасывать координату с наибольшей дельтой округления и воссоздавать её из значений двух других. Но так как нам нужны только X и Z, мы можем не утруждаться воссозданием Y.

		if (iX + iY + iZ != 0) {
			float dX = Mathf.Abs(x - iX);
			float dY = Mathf.Abs(y - iY);
			float dZ = Mathf.Abs(-x -y - iZ);

			if (dX > dY && dX > dZ) {
				iX = -iY - iZ;
			}
			else if (dZ > dY) {
				iZ = -iX - iY;
			}
		}

Раскраска шестиугольников

Теперь, когда мы можем касаться верной ячейки, настало время для настоящего взаимодействия. Давайте будем менять цвет каждой ячейки, в которую попадём. Добавим для HexGrid настраиваемые цвета ячейки по умолчанию и затронутой ячейки.

	public Color defaultColor = Color.white;
	public Color touchedColor = Color.magenta;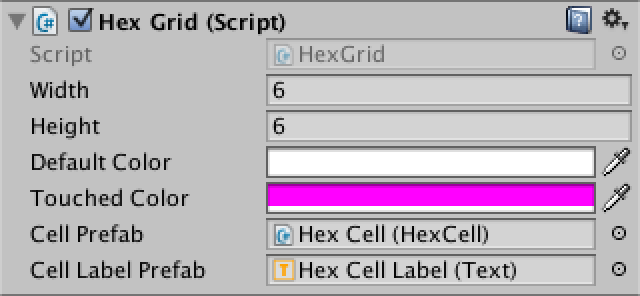

Выбор цвета ячеек.

Добавим к HexCell общее поле цвета.

public class HexCell : MonoBehaviour {

	public HexCoordinates coordinates;

	public Color color;
}

Назначим ему в HexGrid.CreateCell цвет по умолчанию.

	void CreateCell (int x, int z, int i) {
		…
		cell.coordinates = HexCoordinates.FromOffsetCoordinates(x, z);
		cell.color = defaultColor;
		…
	}

Также нам нужно добавить к HexMesh информацию о цвете.

	List<Color> colors;

	void Awake () {
		…
		vertices = new List<Vector3>();
		colors = new List<Color>();
		…
	}

	public void Triangulate (HexCell[] cells) {
		hexMesh.Clear();
		vertices.Clear();
		colors.Clear();
		…
		hexMesh.vertices = vertices.ToArray();
		hexMesh.colors = colors.ToArray();
		…
	}

Теперь при триангуляции мы должны добавлять к каждому треугольнику ещё и данные о цвете. Для этой цели мы создадим отдельный метод.

	void Triangulate (HexCell cell) {
		Vector3 center = cell.transform.localPosition;
		for (int i = 0; i < 6; i++) {
			AddTriangle(
				center,
				center + HexMetrics.corners[i],
				center + HexMetrics.corners[i + 1]
			);
			AddTriangleColor(cell.color);
		}
	}

	void AddTriangleColor (Color color) {
		colors.Add(color);
		colors.Add(color);
		colors.Add(color);
	}

Вернёмся к HexGrid.TouchCell. Сначала преобразуем координаты ячейки в соответствующий индекс массива. Для квадратной сетки это было бы просто X плюс Z умножить на ширину, но в нашем случае придётся прибавить ещё и смещение в половину Z. Затем мы берём ячейку, меняем её цвет и снова триангулируем меш.

	public void TouchCell (Vector3 position) {
		position = transform.InverseTransformPoint(position);
		HexCoordinates coordinates = HexCoordinates.FromPosition(position);
		int index = coordinates.X + coordinates.Z * width + coordinates.Z / 2;
		HexCell cell = cells[index];
		cell.color = touchedColor;
		hexMesh.Triangulate(cells);
	}

Хотя теперь мы и можем раскрашивать ячейки, визуальных изменений пока не видно. Так получилось потому, что шейдер по умолчанию не использует цвета вершин. Нам придётся написать собственный. Создадим новый default shader (Assets / Create / Shader / Default Surface Shader). В него нужно внести всего два изменения. Во-первых, добавим к его входной struct данные цвета. Во-вторых, умножим albedo на этот цвет. Нас интересуют только каналы RGB, потому что материал непрозрачен.

Shader "Custom/VertexColors" {
	Properties {
		_Color ("Color", Color) = (1,1,1,1)
		_MainTex ("Albedo (RGB)", 2D) = "white" {}
		_Glossiness ("Smoothness", Range(0,1)) = 0.5
		_Metallic ("Metallic", Range(0,1)) = 0.0
	}
	SubShader {
		Tags { "RenderType"="Opaque" }
		LOD 200
		
		CGPROGRAM
		#pragma surface surf Standard fullforwardshadows
		#pragma target 3.0

		sampler2D _MainTex;

		struct Input {
			float2 uv_MainTex;
			<mark>float4 color : COLOR;</mark>
		};

		half _Glossiness;
		half _Metallic;
		fixed4 _Color;

		void surf (Input IN, inout SurfaceOutputStandard o) {
			fixed4 c = tex2D(_MainTex, IN.uv_MainTex) * _Color;
			o.Albedo = c.rgb <mark>* IN.color</mark>;
			o.Metallic = _Metallic;
			o.Smoothness = _Glossiness;
			o.Alpha = c.a;
		}
		ENDCG
	}
	FallBack "Diffuse"
}

Создадим новый материал, использующий этот шейдер, а потом сделаем так, чтобы меш сетки использовал этот материал. Благодаря этому появятся цвета ячеек.

Раскрашенные ячейки.

unitypackage

Редактор карты

Теперь, когда мы знаем, как изменять цвета, давайте создадим простой внутриигровой редактор. Этот функционал не относится к возможностями HexGrid, поэтому превратим TouchCell в общий метод с дополнительным параметром цвета. Также удалим поле touchedColor.

public void ColorCell (Vector3 position, Color color) {
		position = transform.InverseTransformPoint(position);
		HexCoordinates coordinates = HexCoordinates.FromPosition(position);
		int index = coordinates.X + coordinates.Z * width + coordinates.Z / 2;
		HexCell cell = cells[index];
		cell.color = color;
		hexMesh.Triangulate(cells);
	}

Создадим компонент HexMapEditor и переместим в него методы Update и HandleInput. Добавим ему общее поле, чтобы ссылаться на сетку шестиугольников, массив цветов и частное поле для отслеживания активного цвета. Наконец, добавим общий метод для выбора цвета и заставим его изначально выбирать первый цвет.

using UnityEngine;

public class HexMapEditor : MonoBehaviour {

	public Color[] colors;

	public HexGrid hexGrid;

	private Color activeColor;

	void Awake () {
		SelectColor(0);
	}

	void Update () {
		if (Input.GetMouseButton(0)) {
			HandleInput();
		}
	}

	void HandleInput () {
		Ray inputRay = Camera.main.ScreenPointToRay(Input.mousePosition);
		RaycastHit hit;
		if (Physics.Raycast(inputRay, out hit)) {
			hexGrid.ColorCell(hit.point, activeColor);
		}
	}

	public void SelectColor (int index) {
		activeColor = colors[index];
	}
}

Добавим ещё один canvas, на этот раз сохранив настройки по умолчанию. Добавьте к нему компонент HexMapEditor, задайте несколько цветов и соедините с сеткой шестиугольников. На этот раз нам понадобится объект event system, и он снова создался автоматически.

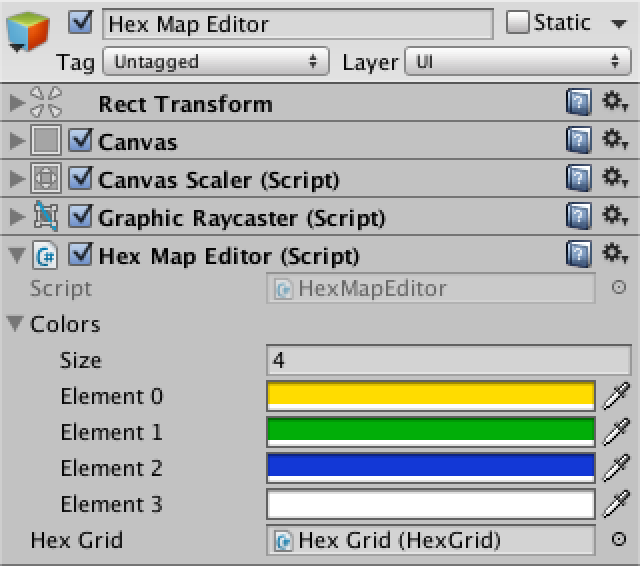
Редактор карты из шестиугольников с четырьмя цветами.

Добавим на canvas панель для хранения селекторов цвета (GameObject / UI / Panel). Добавим ей toggle group (Components / UI/ Toggle Group). Сделаем панель маленькой и разместим её в углу экрана.

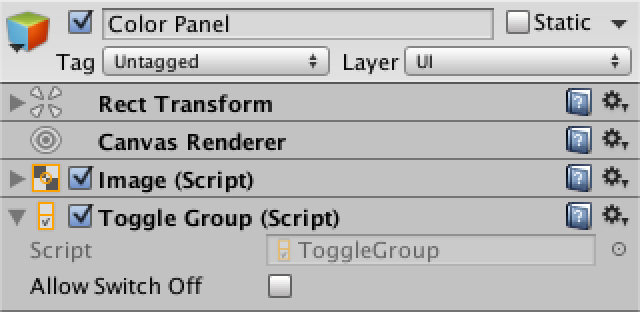
Панель цветов с toggle group.

Теперь заполним панель переключателями для каждого цвета (GameObject / UI / Toggle). Пока мы не будем утруждаться созданием сложного UI, достаточно и простой ручной настройки.

По одному переключателю на каждый цвет.

Включите первый переключатель. Также сделайте все переключатели частями toggle group, чтобы одновременно можно было выбрать только один из них. Наконец, подключите их к методу SelectColor нашего редактора. Это можно сделать кнопкой "+" UI события On Value Changed. Выберите объект редактора карт, затем выберите нужный метод из раскрывающегося списка.

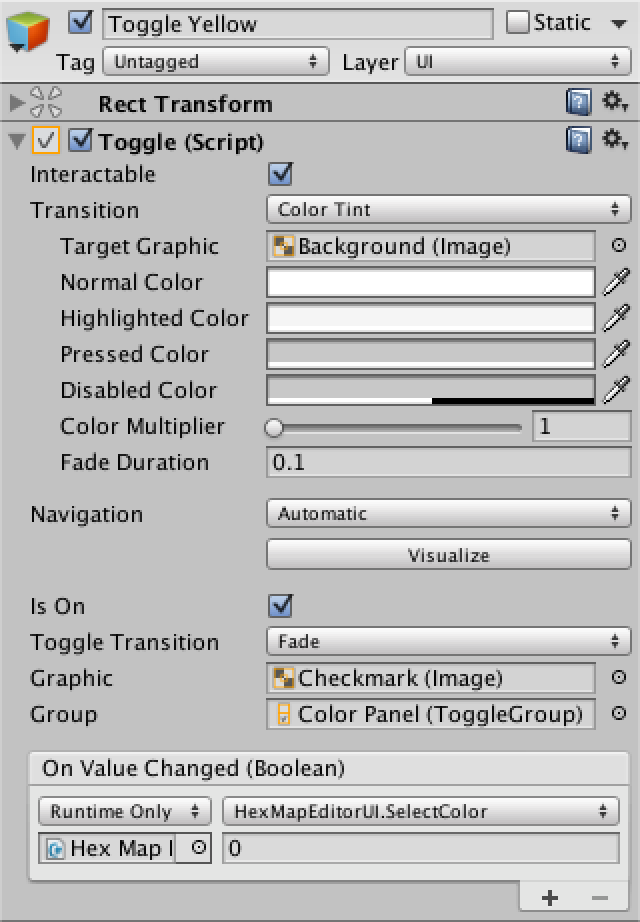
Первый переключатель.

Это событие передаёт булев аргумент, определяющий, включен ли переключатель при каждом его изменении. Но нас это не волнует. Вместо этого нам придётся вручную передавать целочисленный аргумент, соответствующий индексу цвета, который мы хотим использовать. Поэтому оставьте для первого переключателя значение 0, для второго задайте значение 1, и так далее.

Раскрашивание несколькими цветами.

Хотя UI и работает, есть одна раздражающая деталь. Чтобы увидеть её, переместите панель так, чтобы она закрывала сетку шестиугольников. При выборе нового цвета мы также будем раскрашивать ячейки, находящиеся под UI. То есть мы одновременно взаимодействуем с UI и с сеткой. Это нежелательное поведение.

Это можно исправить, спрашивая систему событий, определила ли она расположение курсора над каким-то объектом. Так как она знает только об объектах UI, это будет сообщать нам, что мы взаимодействуем с UI. Поэтому обрабатывать ввод самостоятельно нам нужно будет, только если этого не происходит.

using UnityEngine;
using UnityEngine.EventSystems;
	
	…
	
	void Update () {
		if (
			Input.GetMouseButton(0) &&
			!EventSystem.current.IsPointerOverGameObject()
		) {
			HandleInput();
		}
	}

unitypackage

Часть 2: смешение цветов ячеек

Оглавление

• Соединяем соседей.
• Интерполируем цвета между треугольниками.
• Создаём области смешения.
• Упрощаем геометрию.

В предыдущей части мы заложили основы сетки и добавили возможность редактирования ячеек. Каждая ячейка имеет свой сплошной цвет и цвета на границах ячеек меняются резко. В этом туториале мы создадим переходные зоны, смешивающие цвета соседних ячеек.

Сглаженные переходы между ячейками.

Соседние ячейки

Прежде чем выполнить сглаживание между цветами ячеек, нам нужно узнать, какие из ячеек соседствуют друг с другом. У каждой ячейки есть шесть соседей, которые можно обозначить по направлениям сторон света. Мы получим следующие направления: северо-восток, восток, юго-восток, юго-запад, запад и северо-запад. Давайте создадим для них перечисление и вставим его в отдельный файл скрипта.

public enum HexDirection {
	NE, E, SE, SW, W, NW
}

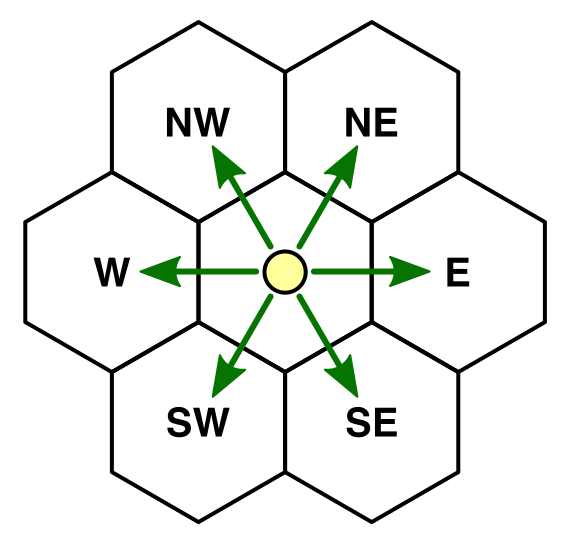
Шесть соседей, шесть направлений.

Для хранения этих соседей добавим к HexCell массив. Хоть мы и можем сделать его общим, но вместо этого сделаем частным и будем предоставлять доступ к методами с помощью направлений. Также сделаем его сериализуемым, чтобы связи не терялись при рекомпиляции.

	[SerializeField]
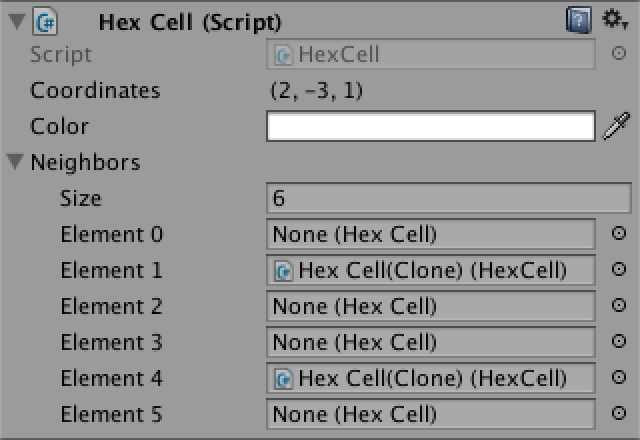
	HexCell[] neighbors;

Теперь массив соседей отображается в инспекторе. Так как у каждой ячейки есть по шесть соседей, то для нашего префаба Hex Cell зададим размер массива 6.

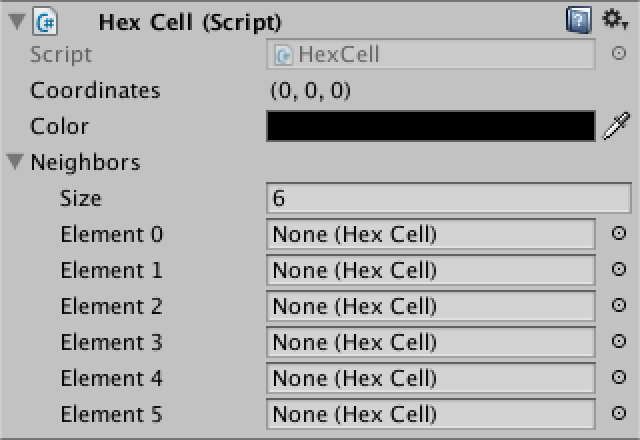
В нашем префабе есть место для шести соседей.

Теперь добавим общий метод для получения соседа ячейки в одном направлении. Так как значение направления всегда находится в интервале от 0 до 5, то нам не нужно проверять, находится ли индекс в пределах массива.

	public HexCell GetNeighbor (HexDirection direction) {
		return neighbors[(int)direction];
	}

Добавим также метод для задания соседа.

	public void SetNeighbor (HexDirection direction, HexCell cell) {
		neighbors[(int)direction] = cell;
	}

Отношения соседей двунаправлены. Поэтому при задании соседа в одном направлении логично будет сразу же задавать соседа и в противоположном направлении.

	public void SetNeighbor (HexDirection direction, HexCell cell) {
		neighbors[(int)direction] = cell;
		cell.neighbors[(int)direction.Opposite()] = this;
	}

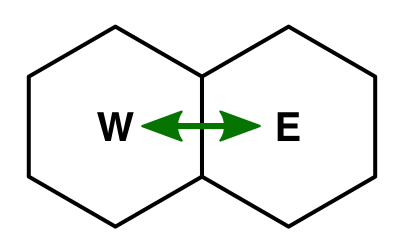
Соседи в противоположных направлениях.

Разумеется, это предполагает, что мы можем запросить направление для противоположного соседа. Мы можем реализовать это, создав расширяющий метод для HexDirection. Для получения противоположного направления нужно прибавить к исходному 3. Однако это работает только для первых трёх направлений, для остальных придётся вычитать 3.

public enum HexDirection {
	NE, E, SE, SW, W, NW
}

public static class HexDirectionExtensions {

	public static HexDirection Opposite (this HexDirection direction) {
		return (int)direction < 3 ? (direction + 3) : (direction - 3);
	}
}

Соединение соседей

Мы можем инициализировать связь соседей в HexGrid.CreateCell. При обходе ячеек строка за строкой, слева направо, мы знаем, какие ячейки уже были созданы. Это ячейки, с которыми мы можем соединиться.

Простейшим является соединение E–W. Первая ячейка каждой строки не имеет восточного соседа. Но у всех остальных ячеек он есть. И эти соседи созданы до ячейки, с которой мы работаем в текущий момент. Поэтому мы можем их соединить.

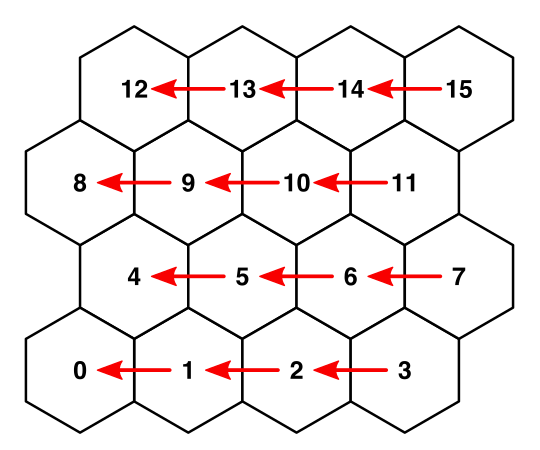
Соединение из E в W в процессе создания ячеек.

	void CreateCell (int x, int z, int i) {
		…
		cell.color = defaultColor;

		if (x > 0) {
			cell.SetNeighbor(HexDirection.W, cells[i - 1]);
		}

		Text label = Instantiate<Text>(cellLabelPrefab);
		…
	}

Восточный и западный сосед соединены.

Нам нужно создать ещё два двунаправленных соединения. Так как это соединения между разными строками сетки, мы можем связываться только с предыдущей строкой. Это значит, что мы полностью должны пропустить первую строку.

		if (x > 0) {
			cell.SetNeighbor(HexDirection.W, cells[i - 1]);
		}
		if (z > 0) {
		}

Так как строки идут зигзагом, их нужно обрабатывать по-разному. Давайте сначала разберёмся с чётными строками. Так как все ячейки в таких строках имеют соседа на SE, мы можем соединить их с ним.

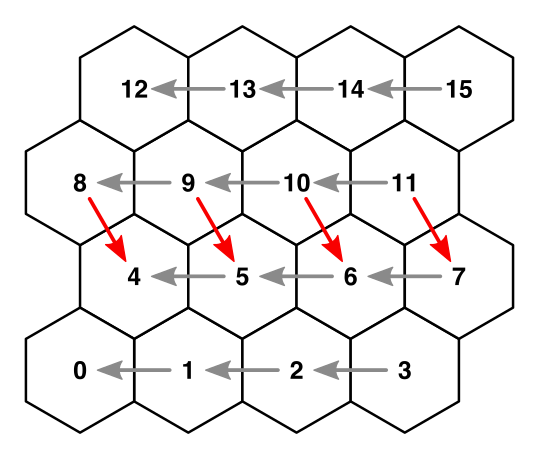
Соединение из NW в SE для чётных строк.

		if (z > 0) {
			if ((z & 1) == 0) {
				cell.SetNeighbor(HexDirection.SE, cells[i - width]);
			}
		}

Мы можем соединиться и с соседями на SW, кроме первой ячейки каждой строки, у которой его нет.

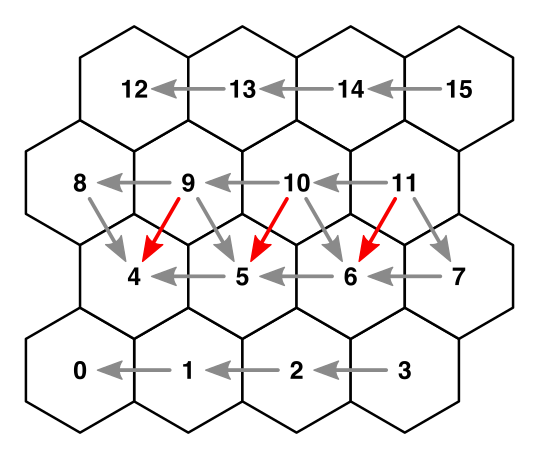
Соединение из NE в SW для чётных строк.

		if (z > 0) {
			if ((z & 1) == 0) {
				cell.SetNeighbor(HexDirection.SE, cells[i - width]);
				if (x > 0) {
					cell.SetNeighbor(HexDirection.SW, cells[i - width - 1]);
				}
			}
		}

Нечётные строки следуют той же логике, но в зеркальном отражении. После завершения этого процесса все соседи в нашей сетке оказываются соединёнными.

		if (z > 0) {
			if ((z & 1) == 0) {
				cell.SetNeighbor(HexDirection.SE, cells[i - width]);
				if (x > 0) {
					cell.SetNeighbor(HexDirection.SW, cells[i - width - 1]);
				}
			}
			else {
				cell.SetNeighbor(HexDirection.SW, cells[i - width]);
				if (x < width - 1) {
					cell.SetNeighbor(HexDirection.SE, cells[i - width + 1]);
				}
			}
		}

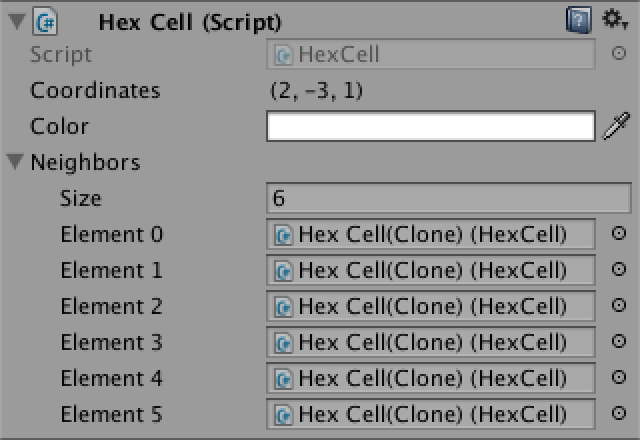
Все соседи соединены.

Разумеется, не каждая ячейка соединена ровно с шестью соседями. У ячеек на границе сетки не меньше двух и не больше пяти соседей. И это необходимо учитывать.

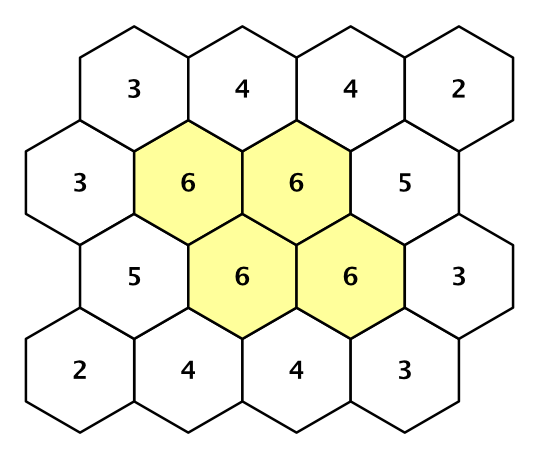
Соседи для каждой ячейки.

unitypackage

Смешение цветов

Смешение цветов усложнит триангуляцию каждой ячейки. Поэтому давайте выделим код триангуляции в отдельную часть. Так как теперь у нас есть направления, давайте для обозначения частей используем их, а не числовые индексы.

	void Triangulate (HexCell cell) {
		for (HexDirection d = HexDirection.NE; d <= HexDirection.NW; d++) {
			Triangulate(d, cell);
		}
	}

	void Triangulate (HexDirection direction, HexCell cell) {
		Vector3 center = cell.transform.localPosition;
		AddTriangle(
			center,
			center + HexMetrics.corners[(int)direction],
			center + HexMetrics.corners[(int)direction + 1]
		);
		AddTriangleColor(cell.color);
	}

Теперь, когда мы используем направления, было бы удобно получать углы с направлениями, а не выполнять преобразование в индексы.

		AddTriangle(
			center,
			center + HexMetrics.GetFirstCorner(direction),
			center + HexMetrics.GetSecondCorner(direction)
		);

Для этого необходимо добавить в HexMetrics два статических метода. В качестве бонуса это позволяет нам сделать массив углов частным.

	static Vector3[] corners = {
		new Vector3(0f, 0f, outerRadius),
		new Vector3(innerRadius, 0f, 0.5f * outerRadius),
		new Vector3(innerRadius, 0f, -0.5f * outerRadius),
		new Vector3(0f, 0f, -outerRadius),
		new Vector3(-innerRadius, 0f, -0.5f * outerRadius),
		new Vector3(-innerRadius, 0f, 0.5f * outerRadius),
		new Vector3(0f, 0f, outerRadius)
	};

	public static Vector3 GetFirstCorner (HexDirection direction) {
		return corners[(int)direction];
	}

	public static Vector3 GetSecondCorner (HexDirection direction) {
		return corners[(int)direction + 1];
	}

Несколько цветов на треугольник

Пока у метода HexMesh.AddTriangleColor есть только один аргумент цвета. Он может создавать треугольник только со сплошным цветом. Давайте создадим альтернативу, поддерживающую отдельные цвета для каждой вершины.

	void AddTriangleColor (Color c1, Color c2, Color c3) {
		colors.Add(c1);
		colors.Add(c2);
		colors.Add(c3);
	}

Теперь мы можем приступить к смешению цветов! Начнём с простого использования цвета соседа для двух других вершин.

	void Triangulate (HexDirection direction, HexCell cell) {
		Vector3 center = cell.transform.localPosition;
		AddTriangle(
			center,
			center + HexMetrics.GetFirstCorner(direction),
			center + HexMetrics.GetSecondCorner(direction)
		);
		HexCell neighbor = cell.GetNeighbor(direction);
		AddTriangleColor(cell.color, neighbor.color, neighbor.color);
	}

К сожалению, это приводит к NullReferenceException, потому что у ячеек на границе нет шести соседей. Как нам поступить при нехватке соседа? Давайте будем прагматичными и используем в качестве замены саму ячейку.

		HexCell neighbor = cell.GetNeighbor(direction) ?? cell;

Смешение цветов есть, но выполнено неверно.

Усреднение цветов

Смешение цветов работает, но получающиеся результаты очевидно неверны. Цвет на рёбрах шестиугольников должен быть средним от двух соседних ячеек.

		HexCell neighbor = cell.GetNeighbor(direction) ?? cell;
		Color edgeColor = (cell.color + neighbor.color) * 0.5f;
		AddTriangleColor(cell.color, edgeColor, edgeColor);

Смешение на рёбрах.
Хотя мы и выполняет смешение на рёбрах, всё равно получаются резкие границы цветов. Это происходит, потому что каждая вершина шестиугольника является общей для трёх шестиугольников.

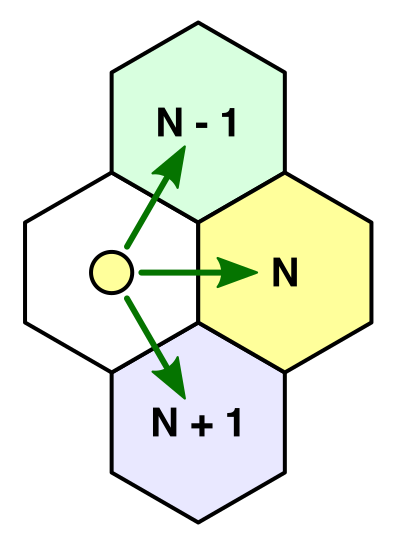
Три соседа, четыре цвета.

Это значит, что нам нужно также учитывать соседей в предыдущем и следующем направлениях. То есть у нас получается четыре цвета в двух наборах по три.

Давайте добавим в HexDirectionExtensions два метода сложения для удобного перехода к предыдущему и следующему направлениям.

	public static HexDirection Previous (this HexDirection direction) {
		return direction == HexDirection.NE ? HexDirection.NW : (direction - 1);
	}

	public static HexDirection Next (this HexDirection direction) {
		return direction == HexDirection.NW ? HexDirection.NE : (direction + 1);
	}

Теперь мы можем получать всех трёх соседей и выполнять трёхсторонее смешение.

		HexCell prevNeighbor = cell.GetNeighbor(direction.Previous()) ?? cell;
		HexCell neighbor = cell.GetNeighbor(direction) ?? cell;
		HexCell nextNeighbor = cell.GetNeighbor(direction.Next()) ?? cell;
		
		AddTriangleColor(
			cell.color,
			(cell.color + prevNeighbor.color + neighbor.color) / 3f,
			(cell.color + neighbor.color + nextNeighbor.color) / 3f
		);

Смешение на углах.

Так мы получаем правильные переходы цветов, за исключением границы сетки. Ячейки границы не согласуются с цветами отсутствующих соседей, поэтому здесь мы по-прежнему видим резкие границы. Однако в целом наш нынешний подход не даёт хороших результатов. Нам нужна стратегия получше.

unitypackage

Области смешения

Смешение по всей поверхности шестиугольника приводит к размытому хаосу. Мы не можем чётко увидеть отдельные ячейки. Можно сильно улучшить результаты, выполняя смешение только рядом с рёбрами шестиугольников. При этом внутренняя область шестиугольников сохранит сплошную окраску.

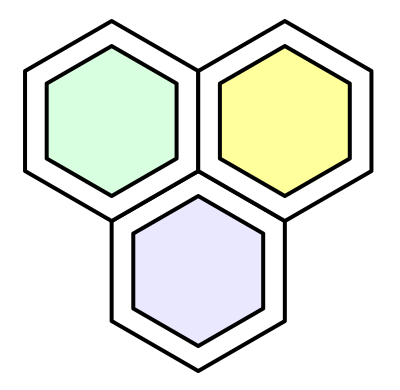
Сплошная закраска центов с областями смешения.

Каким по размерам должна быть сплошная область по сравнению с областью смешения? Разные распределения приводят к разным результатам. Мы определим эту область как долю внешнего радиуса. Пусть она будет равна 75%. Это приведёт нас к двум новым метрикам, в сумме дающим 100%.

	public const float solidFactor = 0.75f;
	
	public const float blendFactor = 1f - solidFactor;

Создав этот новый коэффициент сплошной закраски, мы можем написать методы для получения углов сплошных внутренних шестиугольников.

	public static Vector3 GetFirstSolidCorner (HexDirection direction) {
		return corners[(int)direction] * solidFactor;
	}

	public static Vector3 GetSecondSolidCorner (HexDirection direction) {
		return corners[(int)direction + 1] * solidFactor;
	}

Теперь изменим HexMesh.Triangulate, чтобы он использовать вместо исходных углов эти углы сплошной закраски. Цвета пока оставим такими же.

		AddTriangle(
			center,
			center + HexMetrics.GetFirstSolidCorner(direction),
			center + HexMetrics.GetSecondSolidCorner(direction)
		);

Сплошные шестиугольники без рёбер.

Триангуляция областей смешения

Нам нужно заполнить пустое пространство, которое мы создали при уменьшении треугольников. В каждом из направлений это пространство имеет форму трапецоида. Для его покрытия можно использовать четырёхугольник (quad). Поэтому создадим методы для добавления четырёхугольника и его цветов.

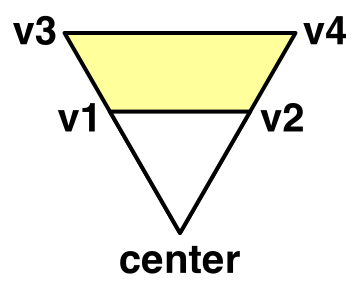
Ребро трапецоида.

	void AddQuad (Vector3 v1, Vector3 v2, Vector3 v3, Vector3 v4) {
		int vertexIndex = vertices.Count;
		vertices.Add(v1);
		vertices.Add(v2);
		vertices.Add(v3);
		vertices.Add(v4);
		triangles.Add(vertexIndex);
		triangles.Add(vertexIndex + 2);
		triangles.Add(vertexIndex + 1);
		triangles.Add(vertexIndex + 1);
		triangles.Add(vertexIndex + 2);
		triangles.Add(vertexIndex + 3);
	}

	void AddQuadColor (Color c1, Color c2, Color c3, Color c4) {
		colors.Add(c1);
		colors.Add(c2);
		colors.Add(c3);
		colors.Add(c4);
	}

Переделаем HexMesh.Triangulate, чтобы треугольник получал один цвет, а четырёхугольник выполнял смешение между сплошным цветом и цветами двух углов.

	void Triangulate (HexDirection direction, HexCell cell) {
		Vector3 center = cell.transform.localPosition;
		Vector3 v1 = center + HexMetrics.GetFirstSolidCorner(direction);
		Vector3 v2 = center + HexMetrics.GetSecondSolidCorner(direction);

		AddTriangle(center, v1, v2);
		AddTriangleColor(cell.color);

		Vector3 v3 = center + HexMetrics.GetFirstCorner(direction);
		Vector3 v4 = center + HexMetrics.GetSecondCorner(direction);

		AddQuad(v1, v2, v3, v4);

		HexCell prevNeighbor = cell.GetNeighbor(direction.Previous()) ?? cell;
		HexCell neighbor = cell.GetNeighbor(direction) ?? cell;
		HexCell nextNeighbor = cell.GetNeighbor(direction.Next()) ?? cell;

		AddQuadColor(
			cell.color,
			cell.color,
			(cell.color + prevNeighbor.color + neighbor.color) / 3f,
			(cell.color + neighbor.color + nextNeighbor.color) / 3f
		);
	}

Смешение с рёбрами трапецоидов.

Мосты между рёбрами

Картина становится лучше, но работа ещё не закончена. Смешение цветов между двумя соседями загрязняется соседними с ребром ячейками. Чтобы избежать этого, нам нужно вырезать углы из трапецоида и превратить его в прямоугольник. После этого он создаст мост между ячейкой и её соседом, оставляя по сторонам пробелы.

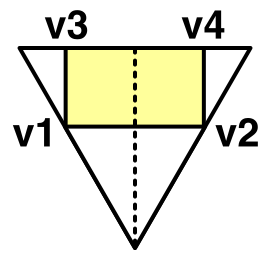
Мост между рёбрами.

Мы можем найти новые позиции v3 и v4, начав с v1 и v2, а затем переместившись вдоль моста прямо до ребра ячейки. Каким же будет смещение моста? Мы можем найти его, взяв среднюю точку между двумя соответствующими углами, а затем применив к ней коэффициент смешения. Этим займётся HexMetrics.

	public static Vector3 GetBridge (HexDirection direction) {
		return (corners[(int)direction] + corners[(int)direction + 1]) *
			0.5f * blendFactor;
	}

Вернёмся к HexMesh, теперь будет логично добавить вариант AddQuadColor, которому требуется только два цвета.

	void AddQuadColor (Color c1, Color c2) {
		colors.Add(c1);
		colors.Add(c1);
		colors.Add(c2);
		colors.Add(c2);
	}

Изменим Triangulate так, чтобы он создавал правильно смешивающиеся мосты между соседями.

		Vector3 bridge = HexMetrics.GetBridge(direction);
		Vector3 v3 = v1 + bridge;
		Vector3 v4 = v2 + bridge;

		AddQuad(v1, v2, v3, v4);

		HexCell prevNeighbor = cell.GetNeighbor(direction.Previous()) ?? cell;
		HexCell neighbor = cell.GetNeighbor(direction) ?? cell;
		HexCell nextNeighbor = cell.GetNeighbor(direction.Next()) ?? cell;

		AddQuadColor(cell.color, (cell.color + neighbor.color) * 0.5f);

Правильно раскрашенные мосты с угловыми пробелами.

Заполнение пробелов

Теперь у нас образовался треугольный зазор в местах соединения трёх ячеек. Мы получили эти пробелы, вырезав треугольные стороны трапецоидов. Давайте вернём эти треугольники обратно.

Сначала рассмотрим треугольник, соединяющийся с предыдущим соседом. Его первая вершина имеет цвет ячейки. Цветом второй вершины будет смешение трёх цветов. И последняя вершина будет иметь тот же цвет, что и точка посередине моста.

		Color bridgeColor = (cell.color + neighbor.color) * 0.5f;
		AddQuadColor(cell.color, bridgeColor);

		AddTriangle(v1, center + HexMetrics.GetFirstCorner(direction), v3);
		AddTriangleColor(
			cell.color,
			(cell.color + prevNeighbor.color + neighbor.color) / 3f,
			bridgeColor
		);

Почти всё готово.

Другой треугольник работает таким же образом, за исключением того, что моста касается не третья, а вторая вершина.

		AddTriangle(v2, v4, center + HexMetrics.GetSecondCorner(direction));
		AddTriangleColor(
			cell.color,
			bridgeColor,
			(cell.color + neighbor.color + nextNeighbor.color) / 3f
		);

Полная раскраска.

Теперь у нас есть красивые области смешения, которым мы можем придать любой размер. Рёбра можно сделать размытыми или резкими, как захотите. Но можно заметить, что смешение рядом с границей сетки всё равно реализуется неверно. И мы снова оставим это на потом, сосредоточившись пока на другой теме.

unitypackage

Слияние рёбер

Взгляните на топологию нашей сетки. Какие формы здесь заметны? Если не обращать внимания на границу, то мы можем выделить три отдельных типа форм. Тут есть одноцветные шестиугольники, двухцветные прямоугольники и трёхцветные треугольники. Все эти три цвета возникают в точке соединения трёх ячеек.

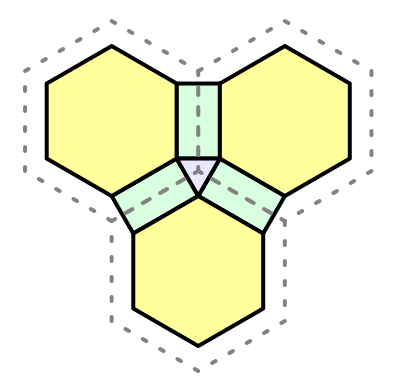
Три визуальные структуры.

Итак, каждые два шестиугольника соединены одним прямоугольным мостом. А каждые три шестиугольника соединены одним треугольником. Однако мы выполняем более сложную триангуляцию. Сейчас мы используем для соединения пары шестиугольников два четырёхугольника вместо одного. А для соединения трёх шестиугольников мы используем шесть треугольников. Это слишком избыточно. Кроме того, если бы мы непосредственно выполняли соединение с одной фигурой, то нам не потребовалось бы никакое усреднение цветов. Поэтому нам бы удалось обойтись меньшей сложностью, меньшими трудами и меньшим количеством треугольников.

Сложнее, чем нужно.

Соединение мостами напрямую

Сейчас наши мосты между рёбрами состоят из двух четырёхугольников. Чтобы продлить их до следующего шестиугольника, нам нужно удвоить длину моста. Это означает, что нам больше не нужно усреднять два угла HexMetrics.GetBridge. Вместо этого мы просто добавляем их, а затем умножаем на коэффициент смешения.

	public static Vector3 GetBridge (HexDirection direction) {
		return (corners[(int)direction] + corners[(int)direction + 1]) *
			blendFactor;
	}

Мосты растянулись на всю длину и наложились друг на друга.

Теперь мосты создают прямые соединения между шестиугольниками. Но мы по-прежнему генерируем по два четырёхугольника на соединение, по одному в каждом направлении. То есть создавать мосты между двумя ячейками должна только одна из них.

Давайте для начала упростим наш код триангуляции. Удалим всё, что касается треугольников рёбер и смешения цветов. Затем переместим в новый метод код, добавляющий четырёхугольник моста. Передадим этому методу первые две вершины, чтобы нам не пришлось вычислять их заново.

	void Triangulate (HexDirection direction, HexCell cell) {
		Vector3 center = cell.transform.localPosition;
		Vector3 v1 = center + HexMetrics.GetFirstSolidCorner(direction);
		Vector3 v2 = center + HexMetrics.GetSecondSolidCorner(direction);

		AddTriangle(center, v1, v2);
		AddTriangleColor(cell.color);

		TriangulateConnection(direction, cell, v1, v2);
	}

	void TriangulateConnection (
		HexDirection direction, HexCell cell, Vector3 v1, Vector3 v2
	) {
		HexCell neighbor = cell.GetNeighbor(direction) ?? cell;
		
		Vector3 bridge = HexMetrics.GetBridge(direction);
		Vector3 v3 = v1 + bridge;
		Vector3 v4 = v2 + bridge;

		AddQuad(v1, v2, v3, v4);
		AddQuadColor(cell.color, neighbor.color);
	}

Теперь мы запросто можем ограничить триангуляцию соединений. Начнём с того, что будем добавлять мост только при работе с соединением NE.

		if (direction == HexDirection.NE) {
			TriangulateConnection(direction, cell, v1, v2);
		}

Мосты только в направлении NE.

Похоже, что мы можем покрыть все соединения, триангулируя их только в первых трёх направлениях: NE, E и SE.

		if (direction <= HexDirection.SE) {
			TriangulateConnection(direction, cell, v1, v2);
		}

Все внутренние мосты и мосты на границах.

Мы покрыли все соединения между двумя соседними ячейками. Но у нас появилось также несколько мостов, ведущих из ячейки в никуда. Давайте избавимся от них, выходя из TriangulateConnection, когда соседи отсутствуют. То есть нам больше не требуется заменять отсутствующих соседей самой ячейкой.

	void TriangulateConnection (
		HexDirection direction, HexCell cell, Vector3 v1, Vector3 v2
	) {
		HexCell neighbor = cell.GetNeighbor(direction);
		if (neighbor == null) {
			return;
		}
		
		…
	}

Только внутренние мосты.

Треугольные соединения

Теперь нам снова нужно закрыть треугольные пробелы. Давайте сделаем это для треугольника, соединяющегося со следующим соседом. И это снова нужно делать только тогда, когда сосед существует.

	void TriangulateConnection (
		HexDirection direction, HexCell cell, Vector3 v1, Vector3 v2
	) {
		…

		HexCell nextNeighbor = cell.GetNeighbor(direction.Next());
		if (nextNeighbor != null) {
			AddTriangle(v2, v4, v2);
			AddTriangleColor(cell.color, neighbor.color, nextNeighbor.color);
		}
	}

Какой будет позиция третьей вершины? Я вставил в качестве замены v2, но это очевидно неверно. Так как каждое ребро этих треугольников соединяется с мостом, мы можем найти её, пройдя по мосту до следующего соседа.

			AddTriangle(v2, v4, v2 + HexMetrics.GetBridge(direction.Next()));

Мы снова делаем полную триангуляцию.

Мы закончили? Пока нет, потому что теперь мы создаём перекрывающиеся треугольники. Так как три ячейки имеют одно общее треугольное соединение, нам нужно добавить их только для двух соединений. Поэтому подойдут NE и E.

		if (direction <= HexDirection.E && nextNeighbor != null) {
			AddTriangle(v2, v4, v2 + HexMetrics.GetBridge(direction.Next()));
			AddTriangleColor(cell.color, neighbor.color, nextNeighbor.color);
		}

unitypackage

Часть 3: высоты

Оглавление

• Добавляем ячейкам высоту.
• Триангулируем склоны.
• Вставляем уступы.
• Объединяем уступы и обрывы.

В этой части туториала мы добавим поддержку разных уровней высоты и создадим между ними специальные переходы.

Высоты и уступы.

Высота ячеек

Мы разделили нашу карту на отдельные ячейки, покрывающие плоскую область. Теперь мы придадим каждой ячейке собственный уровень высоты. Мы будем использовать дискретные уровни высот, чтобы хранить их как целочисленное поле в HexCell.

	public int elevation;

Насколько большим может быть каждый последующий уровень высоты? Мы можем использовать любое значение, поэтому давайте зададим его как ещё одну константу HexMetrics. Мы будем использовать шаг в пять единиц, чтобы переходы были хорошо заметны. В настоящей игре я бы использовал шаг поменьше.

	public const float elevationStep = 5f;

Изменение ячеек

До настоящего момента мы могли изменять только цвет ячейки, но теперь мы можем менять и её высоту. Поэтому метода HexGrid.ColorCell нам уже недостаточно. Кроме того, в дальнейшем мы можем добавить и другие опции редактирования ячеек, поэтому нам требуется новый подход.

Переименуем ColorCell в GetCell и сделаем так, чтобы он вместо задания цвета ячейки возвращал ячейку в заданной позиции. Поскольку этот метод больше ничего не изменяет, нам нужно сразу же триангулировать ячейки.

	public HexCell GetCell (Vector3 position) {
		position = transform.InverseTransformPoint(position);
		HexCoordinates coordinates = HexCoordinates.FromPosition(position);
		int index = coordinates.X + coordinates.Z * width + coordinates.Z / 2;
		return cells[index];
	}

Теперь изменением ячейки будет заниматься редактор. После завершения работы сетку нужно снова триангулировать. Для этого добавим общий метод HexGrid.Refresh.

	public void Refresh () {
		hexMesh.Triangulate(cells);
	}

Изменим HexMapEditor, чтобы он мог работать с новыми методами. Дадим ему новый метод EditCell, который займётся всеми изменениями ячейки, после чего будет обновлять сетку.

	void HandleInput () {
		Ray inputRay = Camera.main.ScreenPointToRay(Input.mousePosition);
		RaycastHit hit;
		if (Physics.Raycast(inputRay, out hit)) {
			EditCell(hexGrid.GetCell(hit.point));
		}
	}

	void EditCell (HexCell cell) {
		cell.color = activeColor;
		hexGrid.Refresh();
	}

Мы можем изменять высоты, просто назначая редактируемой ячейке нужный уровень высоты.

	int activeElevation;

	void EditCell (HexCell cell) {
		cell.color = activeColor;
		cell.elevation = activeElevation;
		hexGrid.Refresh();
	}

Как и в случае с цветами, нам нужен метод для задания активного уровня высоты, который мы свяжем с UI. Для выбора значений из интервала высот мы воспользуемся ползунком. Так как ползунки работают с float, нашему методу требуется параметр типа float. Мы просто будем преобразовывать его в integer.

	public void SetElevation (float elevation) {
		activeElevation = (int)elevation;
	}

Добавим на canvas ползунок (GameObject / Create / Slider) и разместим его под панелью цветов. Сделаем его вертикальным, снизу вверх, чтобы визуально он соответствовал уровням высот. Ограничим его целыми числами и создадим подходящий интервал, например, от 0 до 6. Затем прикрепим его событие On Value Changed к методу SetElevation объекта Hex Map Editor. Метод нужно выбрать из динамического списка, чтобы он вызывался со значением ползунка.

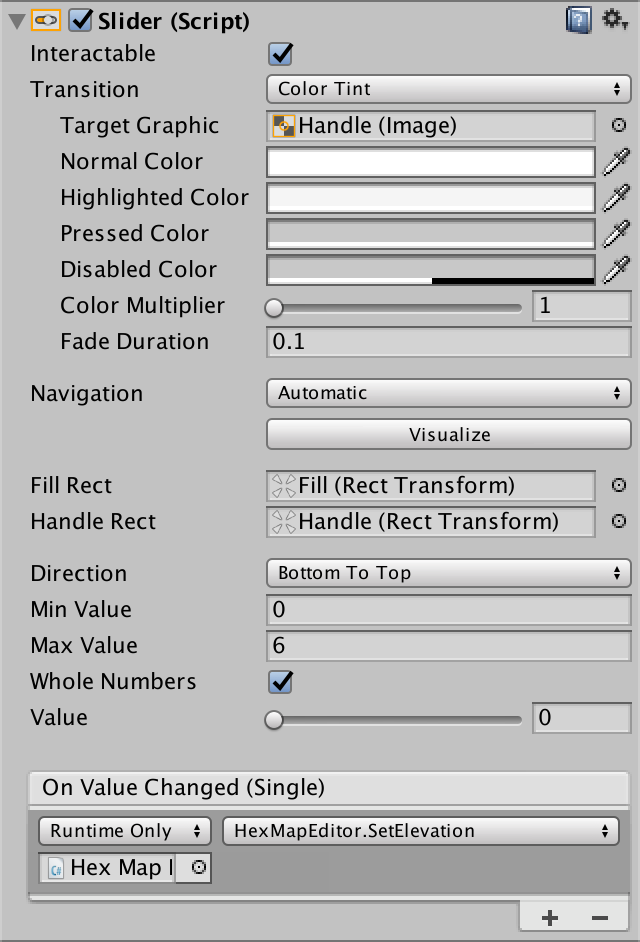
Ползунок высоты.

Визуализация высоты

При изменении ячейки мы теперь задаём и цвет, и высоту. Хотя в инспекторе мы можем видеть, что высота и в самом деле меняется, процесс триангуляции по-прежнему её игнорирует.

Нам достаточно изменять вертикальную локальную позицию ячейки при изменении высоты. Для удобства давайте сделаем метод HexCell.elevation частным и добавим общее свойство HexCell.Elevation.

	public int Elevation {
		get {
			return elevation;
		}
		set {
			elevation = value;
		}
	}
	
	int elevation;

Теперь мы можем изменять вертикальную позицию ячейки при редактировании высоты.

		set {
			elevation = value;
			Vector3 position = transform.localPosition;
			position.y = value * HexMetrics.elevationStep;
			transform.localPosition = position;
		}

Разумеется, для этого требуются небольшие изменения в HexMapEditor.EditCell.

	void EditCell (HexCell cell) {
		cell.color = activeColor;
		cell.Elevation = activeElevation;
		hexGrid.Refresh();
	}

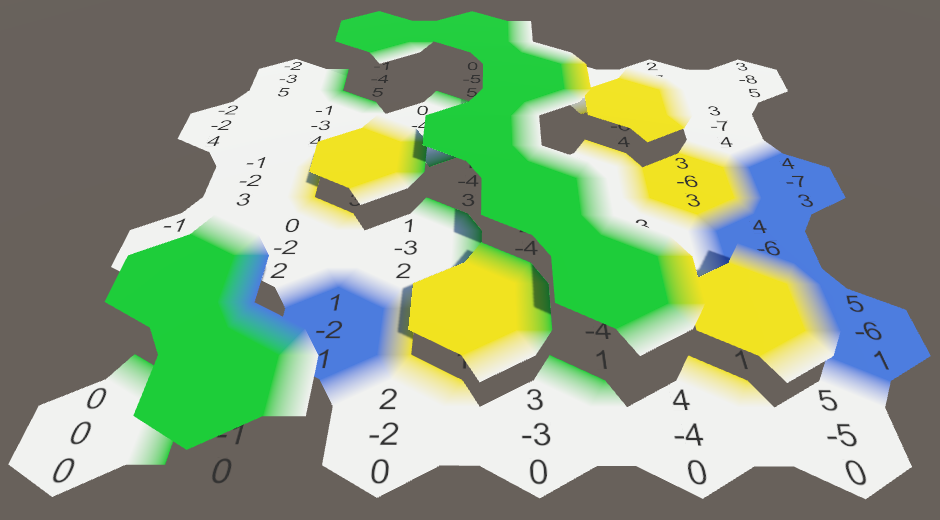
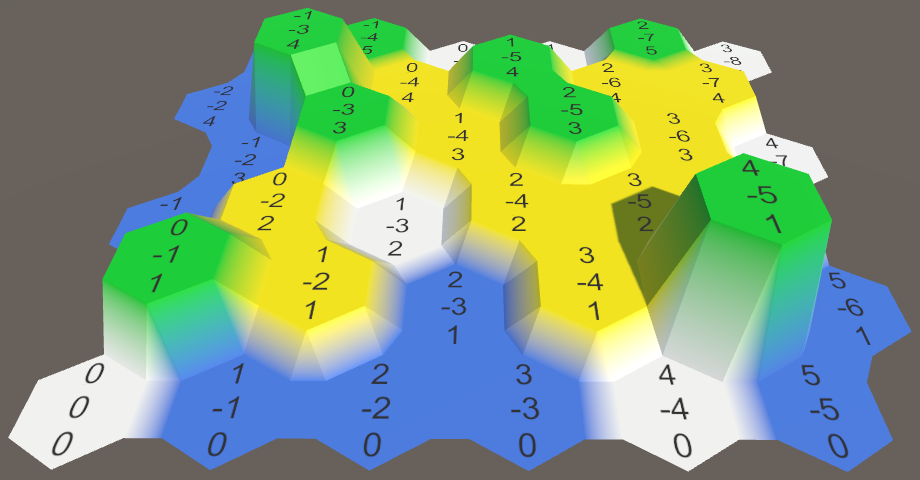
Ячейки с разными высотами.

Теперь высоты ячеек видны, но возникает две проблемы. Во-первых. метки ячеек пропадают под поднятыми ячейками. Во-вторых, соединения между ячейками игнорируют высоту. Давайте это исправим.

Изменяем положение меток ячеек

На текущий момент метки UI для ячеек создаются и размещаются только один раз, после чего мы о них забываем. Для обновления их вертикальных позиций нам нужно их отслеживать. Давайте дадим каждому HexCell ссылку на RectTransform его метки UI, чтобы можно было позже его обновлять.

	public RectTransform uiRect;

Присвоим их в конце HexGrid.CreateCell.

	void CreateCell (int x, int z, int i) {
		…
		cell.uiRect = label.rectTransform;
	}

Теперь мы можем расширить свойство HexCell.Elevation, чтобы оно также изменяло позицию UI ячейки. Так как canvas сетки шестиугольников повёрнут, то метки нужно перемещать в отрицательную сторону по оси Z, а не в положительную сторону оси Y.

		set {
			elevation = value;
			Vector3 position = transform.localPosition;
			position.y = value * HexMetrics.elevationStep;
			transform.localPosition = position;

			Vector3 uiPosition = uiRect.localPosition;
			uiPosition.z = elevation * -HexMetrics.elevationStep;
			uiRect.localPosition = uiPosition;
		}

Метки с учётом высоты.

Создание склонов

Теперь нам нужно преобразовать плоские соединения ячеек в склоны. Это делается в HexMesh.TriangulateConnection. В случае соединений рёбер нам нужно переопределить высоту другого конца моста.

		Vector3 bridge = HexMetrics.GetBridge(direction);
		Vector3 v3 = v1 + bridge;
		Vector3 v4 = v2 + bridge;
		v3.y = v4.y = neighbor.Elevation * HexMetrics.elevationStep;

В случае угловых соединений нам нужно сделать то же самое с мостом к следующему соседу.

		if (direction <= HexDirection.E && nextNeighbor != null) {
			Vector3 v5 = v2 + HexMetrics.GetBridge(direction.Next());
			v5.y = nextNeighbor.Elevation * HexMetrics.elevationStep;
			AddTriangle(v2, v4, v5);
			AddTriangleColor(cell.color, neighbor.color, nextNeighbor.color);
		}

Соединения с учётом высоты.

Теперь у нас есть поддержка ячеек на разных высотах с правильными наклонными соединениями между ними. Но давайте не будем на этом останавливаться. Мы сделаем эти склоны более интересными.

unitypackage

Соединения рёбер с уступами

Прямые склоны выглядят не очень привлекательно. Мы можем разделить их на несколько шагов, добавив уступы. Такой подход используется в игре Endless Legend.

Например, мы можем вставлять на каждый склон по два уступа. В результате один большой склон превращается в три маленьких, между которыми есть две плоские области. Чтобы триангулировать такую схему нам придётся разделять каждое соединение в пять этапов.

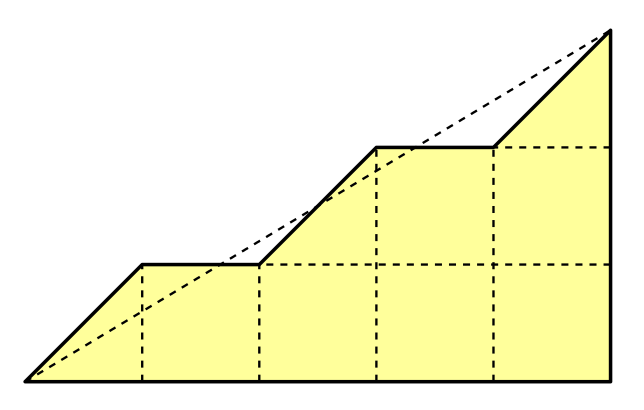
Два уступа на склоне.

Мы можем задать количество уступов для склона в HexMetrics и вычислить исходя из этого количество этапов.

	public const int terracesPerSlope = 2;

	public const int terraceSteps = terracesPerSlope * 2 + 1;

В идеале мы могли бы просто интерполировать каждый шаг вдоль склона. Но это не совсем тривиально, потому что координата Y должна изменяться только на нечётных этапах. Иначе мы не получим плоских уступов. Давайте добавим для этого специальный метод интерполяции HexMetrics.

	public static Vector3 TerraceLerp (Vector3 a, Vector3 b, int step) {
		return a;
	}

Горизонтальная интерполяция выполняется просто, если мы знаем размер шага интерполяции.

	public const float horizontalTerraceStepSize = 1f / terraceSteps;
	
	public static Vector3 TerraceLerp (Vector3 a, Vector3 b, int step) {
		float h = step * HexMetrics.horizontalTerraceStepSize;
		a.x += (b.x - a.x) * h;
		a.z += (b.z - a.z) * h;
		return a;
	}

Чтобы изменять Y только на нечётных этапах, мы можем использовать . Если мы используем целочисленное деление, то оно превратит ряд 1, 2, 3, 4 в 1, 1, 2, 2.

	public const float verticalTerraceStepSize = 1f / (terracesPerSlope + 1);
	
	public static Vector3 TerraceLerp (Vector3 a, Vector3 b, int step) {
		float h = step * HexMetrics.horizontalTerraceStepSize;
		a.x += (b.x - a.x) * h;
		a.z += (b.z - a.z) * h;
		float v = ((step + 1) / 2) * HexMetrics.verticalTerraceStepSize;
		a.y += (b.y - a.y) * v;
		return a;
	}

Давайте добавим метод интерполяции уступов и для цветов. Просто интерполируем их так, как будто соединения плоские.

	public static Color TerraceLerp (Color a, Color b, int step) {
		float h = step * HexMetrics.horizontalTerraceStepSize;
		return Color.Lerp(a, b, h);
	}

Триангуляция

Так как триангуляция соединения рёбер становится сложнее, уберём соответствующий код из HexMesh.TriangulateConnection и поместим его в отдельный метод. В комментариях я сохраню и исходный код, чтобы ссылаться на него в дальнейшем.

	void TriangulateConnection (
		HexDirection direction, HexCell cell, Vector3 v1, Vector3 v2
	) {
		…
		Vector3 bridge = HexMetrics.GetBridge(direction);
		Vector3 v3 = v1 + bridge;
		Vector3 v4 = v2 + bridge;
		v3.y = v4.y = neighbor.Elevation * HexMetrics.elevationStep;

		TriangulateEdgeTerraces(v1, v2, cell, v3, v4, neighbor);
//		AddQuad(v1, v2, v3, v4);
//		AddQuadColor(cell.color, neighbor.color);
		…
	}

	void TriangulateEdgeTerraces (
		Vector3 beginLeft, Vector3 beginRight, HexCell beginCell,
		Vector3 endLeft, Vector3 endRight, HexCell endCell
	) {
		AddQuad(beginLeft, beginRight, endLeft, endRight);
		AddQuadColor(beginCell.color, endCell.color);
	}

Давайте начнём с самого первого этапа процесса. Воспользуемся нашими специальными методами интерполяции для создания первого quad. При этом должен создаться короткий склон, более крутой, чем исходный.

	void TriangulateEdgeTerraces (
		Vector3 beginLeft, Vector3 beginRight, HexCell beginCell,
		Vector3 endLeft, Vector3 endRight, HexCell endCell
	) {
		Vector3 v3 = HexMetrics.TerraceLerp(beginLeft, endLeft, 1);
		Vector3 v4 = HexMetrics.TerraceLerp(beginRight, endRight, 1);
		Color c2 = HexMetrics.TerraceLerp(beginCell.color, endCell.color, 1);

		AddQuad(beginLeft, beginRight, v3, v4);
		AddQuadColor(beginCell.color, c2);
	}

Первый этап создания уступа.

Теперь сразу же перейдём к последнему этапу, пропустив всё, что между ними. Этим мы завершим соединение рёбер, хотя пока и с неверной формой.

		AddQuad(beginLeft, beginRight, v3, v4);
		AddQuadColor(beginCell.color, c2);

		AddQuad(v3, v4, endLeft, endRight);
		AddQuadColor(c2, endCell.color);

Последний этап создания уступа.

Промежуточные этапы можно добавить через цикл. На каждом этапе две последние предыдущие вершины становятся новыми первыми. То же самое относится и к цвету. После вычисления новых векторов и цветов добавляется ещё один quad.

		AddQuad(beginLeft, beginRight, v3, v4);
		AddQuadColor(beginCell.color, c2);

		for (int i = 2; i < HexMetrics.terraceSteps; i++) {
			Vector3 v1 = v3;
			Vector3 v2 = v4;
			Color c1 = c2;
			v3 = HexMetrics.TerraceLerp(beginLeft, endLeft, i);
			v4 = HexMetrics.TerraceLerp(beginRight, endRight, i);
			c2 = HexMetrics.TerraceLerp(beginCell.color, endCell.color, i);
			AddQuad(v1, v2, v3, v4);
			AddQuadColor(c1, c2);
		}

		AddQuad(v3, v4, endLeft, endRight);
		AddQuadColor(c2, endCell.color);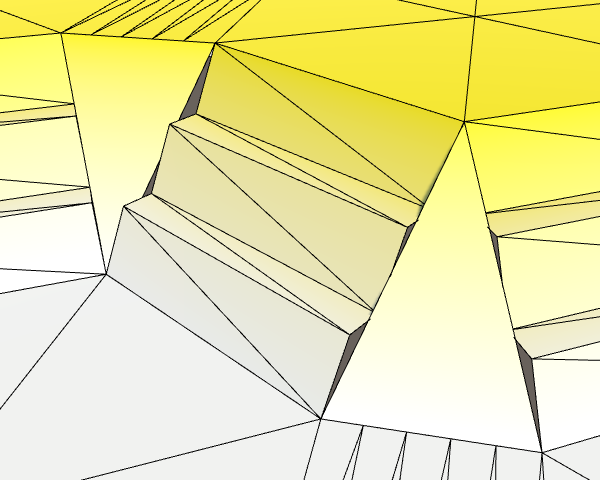

Все промежуточные этапы.

Теперь у всех соединений рёбер есть два уступа, или любое другое количество, которое вы задали в HexMetrics.terracesPerSlope. Разумеется, пока мы не создали уступов для угловых соединений, мы оставим это на потом.

Все соединения рёбер имеют уступы.

unitypackage

Типы соединений

Преобразование всех соединений рёбер в уступы — не такая уж хорошая идея. Они выглядят хорошо, только когда разница высот составляет всего один уровень. Но при большей разнице создаются узкие уступы с большими промежутками между ними, а это выглядит не очень красиво. Кроме того, нам необязательно создавать уступы для всех соединений.

Давайте формализуем это и зададим три типа рёбер: плоскость, склон и обрыв. Создадим для этого перечисление.

public enum HexEdgeType {
	Flat, Slope, Cliff
}

Как определить, с каким типом соединения мы имеем дело? Для этого мы можем добавить в HexMetrics метод, использующий два уровня высоты.

	public static HexEdgeType GetEdgeType (int elevation1, int elevation2) {
	}

Если высоты одинаковы, то у нас будет плоское ребро.

	public static HexEdgeType GetEdgeType (int elevation1, int elevation2) {
		if (elevation1 == elevation2) {
			return HexEdgeType.Flat;
		}
	}

Если разность уровней равна одному шагу, то это склон. Неважно, идёт ли он вверх или вниз. Во всех остальных случаях у нас получается обрыв.

	public static HexEdgeType GetEdgeType (int elevation1, int elevation2) {
		if (elevation1 == elevation2) {
			return HexEdgeType.Flat;
		}
		int delta = elevation2 - elevation1;
		if (delta == 1 || delta == -1) {
			return HexEdgeType.Slope;
		}
		return HexEdgeType.Cliff;
	}

Давайте также добавим удобный метод HexCell.GetEdgeType для получения типа ребра ячейки в определённом направлении.

	public HexEdgeType GetEdgeType (HexDirection direction) {
		return HexMetrics.GetEdgeType(
			elevation, neighbors[(int)direction].elevation
		);
	}

Создание уступов только для склонов

Теперь, когда мы можем определить тип соединения, можно решить, нужно ли вставлять уступы. Изменим HexMesh.TriangulateConnection так, чтобы он создавал уступы только для склонов.

		if (cell.GetEdgeType(direction) == HexEdgeType.Slope) {
			TriangulateEdgeTerraces(v1, v2, cell, v3, v4, neighbor);
		}
//		AddQuad(v1, v2, v3, v4);
//		AddQuadColor(cell.color, neighbor.color);

На этом этапе мы можем раскомментировать ранее закомментированный код, чтобы он занялся обработкой плоскостей и обрывов.

		if (cell.GetEdgeType(direction) == HexEdgeType.Slope) {
			TriangulateEdgeTerraces(v1, v2, cell, v3, v4, neighbor);
		}
		else {
			AddQuad(v1, v2, v3, v4);
			AddQuadColor(cell.color, neighbor.color);
		}

Уступы создаются только на склонах.

unitypackage

Угловые соединения с уступами

Угловые соединения сложнее, чем соединения рёбер, потому что в них участвуют не две, а три ячейки. Каждый угол соединён с тремя рёбрами, которые могут быть плоскостями, склонами или обрывами. Поэтому существует множество возможных конфигураций. Как и в случае с соединениями рёбер, нам лучше добавить в HexMesh новый метод триангуляции.

Нашему новому методу потребуются вершины углового треугольника и соединённые ячейки. Для удобства давайте упорядочим соединения, чтобы знать, какая ячейка имеет наименьшую высоту. После этого мы сможем начать работу снизу влево и вправо.

Угловое соединение.

	void TriangulateCorner (
		Vector3 bottom, HexCell bottomCell,
		Vector3 left, HexCell leftCell,
		Vector3 right, HexCell rightCell
	) {
		AddTriangle(bottom, left, right);
		AddTriangleColor(bottomCell.color, leftCell.color, rightCell.color);
	}

Теперь TriangulateConnection должен определить, какая из ячеек самая нижняя. Сначала проверяем, находится ли триангулируемая ячейка ниже своих соседей или находится на одном уровне с самой нижней. Если это так, то мы можем использовать её как самую нижнюю ячейку.

	void TriangulateConnection (
		HexDirection direction, HexCell cell, Vector3 v1, Vector3 v2
	) {
		…
		
		HexCell nextNeighbor = cell.GetNeighbor(direction.Next());
		if (direction <= HexDirection.E && nextNeighbor != null) {
			Vector3 v5 = v2 + HexMetrics.GetBridge(direction.Next());
			v5.y = nextNeighbor.Elevation * HexMetrics.elevationStep;
			
			if (cell.Elevation <= neighbor.Elevation) {
				if (cell.Elevation <= nextNeighbor.Elevation) {
					TriangulateCorner(v2, cell, v4, neighbor, v5, nextNeighbor);
				}
			}
		}
	}

Если самая глубокая проверка оканчивается неудачей, то это значит, что самой низкой ячейкой является следующий сосед. Для правильной ориентации мы должны повернуть треугольник против часовой стрелки.

			if (cell.Elevation <= neighbor.Elevation) {
				if (cell.Elevation <= nextNeighbor.Elevation) {
					TriangulateCorner(v2, cell, v4, neighbor, v5, nextNeighbor);
				}
				else {
					TriangulateCorner(v5, nextNeighbor, v2, cell, v4, neighbor);
				}
			}

Если неудачей закончилась первая проверка, то нужно сравнивать две соседние ячейки. Если сосед ребра является самым низким, то нужно повернуться по часовой стрелке, в противном случае — против часовой.

			if (cell.Elevation <= neighbor.Elevation) {
				if (cell.Elevation <= nextNeighbor.Elevation) {
					TriangulateCorner(v2, cell, v4, neighbor, v5, nextNeighbor);
				}
				else {
					TriangulateCorner(v5, nextNeighbor, v2, cell, v4, neighbor);
				}
			}
			else if (neighbor.Elevation <= nextNeighbor.Elevation) {
				TriangulateCorner(v4, neighbor, v5, nextNeighbor, v2, cell);
			}
			else {
				TriangulateCorner(v5, nextNeighbor, v2, cell, v4, neighbor);
			}

Поворот против часовой стрелки, нет поворота, поворот по часовой стрелке.

Триангуляция склонов

Чтобы знать, как триангулировать угол, нам нужно понимать, с какими типами рёбер мы имеем дело. Для упрощения этой задачи давайте добавим в HexCell ещё один удобный метод распознавания склона между любыми двумя ячейками.

	public HexEdgeType GetEdgeType (HexCell otherCell) {
		return HexMetrics.GetEdgeType(
			elevation, otherCell.elevation
		);
	}

Используем этот новый метод в HexMesh.TriangulateCorner, чтобы определить типы левого и правого рёбер.

	void TriangulateCorner (
		Vector3 bottom, HexCell bottomCell,
		Vector3 left, HexCell leftCell,
		Vector3 right, HexCell rightCell
	) {
		HexEdgeType leftEdgeType = bottomCell.GetEdgeType(leftCell);
		HexEdgeType rightEdgeType = bottomCell.GetEdgeType(rightCell);

		AddTriangle(bottom, left, right);
		AddTriangleColor(bottomCell.color, leftCell.color, rightCell.color);
	}

Если оба ребра являются склонами, то у нас будут уступы и слева, и справа. Кроме того, поскольку нижняя ячейка является самой низкой, мы знаем, что эти склоны поднимаются вверх. Более того, левая и правая ячейки имеют одинаковую высоту, то есть соединение верхнего ребра является плоским. Мы можем обозначить этот случай как «склон-склон-плоскость», или ССП.

Два склона и плоскость, ССП

Проверим, находимся ли мы в этой ситуации, и если это так, то вызовем новый метод TriangulateCornerTerraces. После этого выполним возврат из метода. Вставим эту проверку перед старым кодом триангуляции, чтобы он заменил исходный треугольник.

	void TriangulateCorner (
		Vector3 bottom, HexCell bottomCell,
		Vector3 left, HexCell leftCell,
		Vector3 right, HexCell rightCell
	) {
		HexEdgeType leftEdgeType = bottomCell.GetEdgeType(leftCell);
		HexEdgeType rightEdgeType = bottomCell.GetEdgeType(rightCell);

		if (leftEdgeType == HexEdgeType.Slope) {
			if (rightEdgeType == HexEdgeType.Slope) {
				TriangulateCornerTerraces(
					bottom, bottomCell, left, leftCell, right, rightCell
				);
				return;
			}
		}

		AddTriangle(bottom, left, right);
		AddTriangleColor(bottomCell.color, leftCell.color, rightCell.color);
	}
	
	void TriangulateCornerTerraces (
		Vector3 begin, HexCell beginCell,
		Vector3 left, HexCell leftCell,
		Vector3 right, HexCell rightCell
	) {
		
	}

Поскольку мы не делаем ничего внутри TriangulateCornerTerraces, некоторые угловые соединения с двумя склонами станут пустотами. Станет ли соединение пустотой, или нет, зависит от того, какая из ячеек окажется нижней.

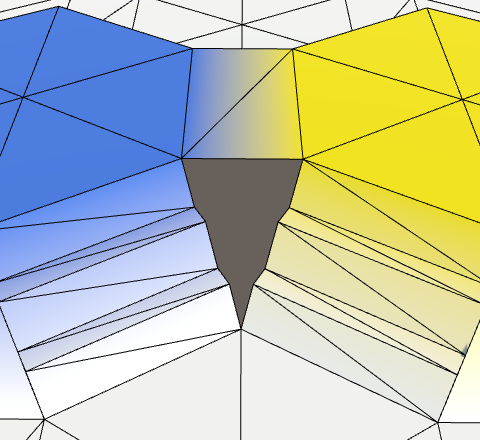
Возникает пустота.

Чтобы заполнить пустоту, нам нужно соединить левый и правый уступ через пробел. Подход здесь такой же, как и для соединения рёбер, но внутри трёхцветного треугольника вместо двухцветного четырёхугольника. Давайте снова начнём с первого этапа, который сейчас является треугольником.

	void TriangulateCornerTerraces (
		Vector3 begin, HexCell beginCell,
		Vector3 left, HexCell leftCell,
		Vector3 right, HexCell rightCell
	) {
		Vector3 v3 = HexMetrics.TerraceLerp(begin, left, 1);
		Vector3 v4 = HexMetrics.TerraceLerp(begin, right, 1);
		Color c3 = HexMetrics.TerraceLerp(beginCell.color, leftCell.color, 1);
		Color c4 = HexMetrics.TerraceLerp(beginCell.color, rightCell.color, 1);

		AddTriangle(begin, v3, v4);
		AddTriangleColor(beginCell.color, c3, c4);
	}

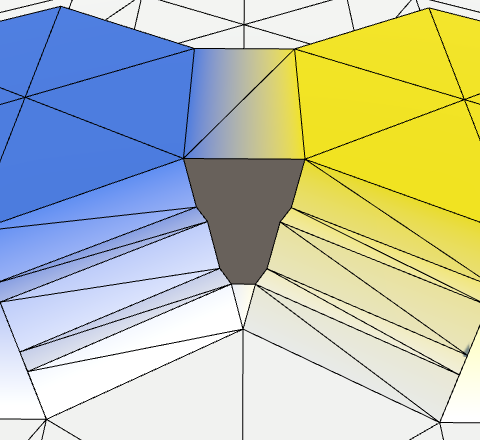
Первый этап треугольника.

И мы снова перейдём сразу к последнему этапу. Это четырёхугольник, образующий трапецоид. Единственное отличие от соединений рёбер здесь в том, что мы имеем дело не с двумя, а четырьмя цветами.

		AddTriangle(begin, v3, v4);
		AddTriangleColor(beginCell.color, c3, c4);

		AddQuad(v3, v4, left, right);
		AddQuadColor(c3, c4, leftCell.color, rightCell.color);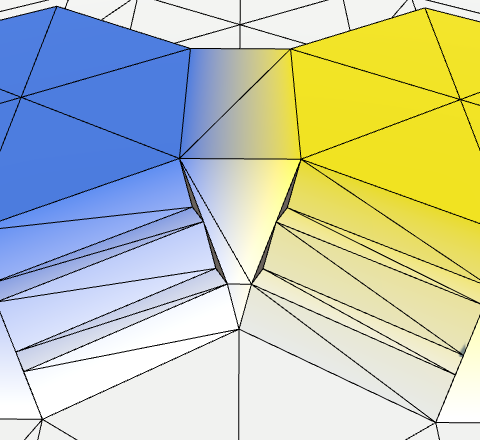

Последний этап четырёхугольника.

Все этапы между ними тоже являются четырёхугольниками.

		AddTriangle(begin, v3, v4);
		AddTriangleColor(beginCell.color, c3, c4);

		for (int i = 2; i < HexMetrics.terraceSteps; i++) {
			Vector3 v1 = v3;
			Vector3 v2 = v4;
			Color c1 = c3;
			Color c2 = c4;
			v3 = HexMetrics.TerraceLerp(begin, left, i);
			v4 = HexMetrics.TerraceLerp(begin, right, i);
			c3 = HexMetrics.TerraceLerp(beginCell.color, leftCell.color, i);
			c4 = HexMetrics.TerraceLerp(beginCell.color, rightCell.color, i);
			AddQuad(v1, v2, v3, v4);
			AddQuadColor(c1, c2, c3, c4);
		}

		AddQuad(v3, v4, left, right);
		AddQuadColor(c3, c4, leftCell.color, rightCell.color);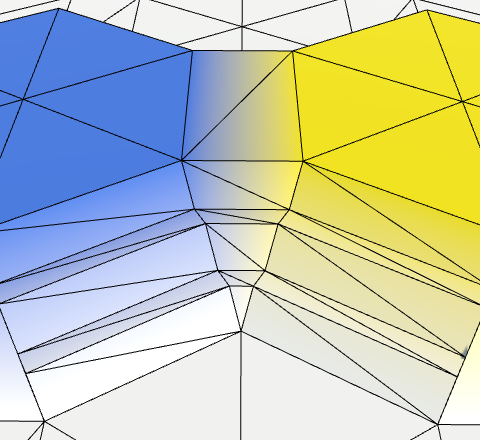

Все этапы.

Вариации с двумя склонами

Случай с двумя склонами имеет две вариации с различными ориентациями, зависящими от того, какая из ячеек окажется нижней. Мы можем найти их, проверяя комбинации левых-правых на склон-плоскость и плоскость-склон.

СПС и ПСС.

Если правое ребро плоское, то мы должны начать создавать уступы слева, а не снизу. Если левое ребро плоское, то нужно начинать справа.

		if (leftEdgeType == HexEdgeType.Slope) {
			if (rightEdgeType == HexEdgeType.Slope) {
				TriangulateCornerTerraces(
					bottom, bottomCell, left, leftCell, right, rightCell
				);
				return;
			}
			if (rightEdgeType == HexEdgeType.Flat) {
				TriangulateCornerTerraces(
					left, leftCell, right, rightCell, bottom, bottomCell
				);
				return;
			}
		}
		if (rightEdgeType == HexEdgeType.Slope) {
			if (leftEdgeType == HexEdgeType.Flat) {
				TriangulateCornerTerraces(
					right, rightCell, bottom, bottomCell, left, leftCell
				);
				return;
			}
		}

Благодаря этому уступы будут огибать ячейки без прерываний, пока не дойдут до обрыва или конца карты.

Сплошные уступы.

unitypackage

Слияние склонов и обрывов

А как насчёт соединения склона и обрыва? Если мы знаем, что левое ребро является склоном, а правое — обрывом, то каким будет верхнее ребро? Оно не может быть плоским, но может быть или склоном, или обрывом.

СОС и СОО.

Давайте добавим новый метод, чтобы он обрабатывал все случаи «склон-обрыв».

	void TriangulateCornerTerracesCliff (
		Vector3 begin, HexCell beginCell,
		Vector3 left, HexCell leftCell,
		Vector3 right, HexCell rightCell
	) {
		
	}

Он должен вызываться как последний вариант в TriangulateCorner, когда левое ребро является склоном.

		if (leftEdgeType == HexEdgeType.Slope) {
			if (rightEdgeType == HexEdgeType.Slope) {
				TriangulateCornerTerraces(
					bottom, bottomCell, left, leftCell, right, rightCell
				);
				return;
			}
			if (rightEdgeType == HexEdgeType.Flat) {
				TriangulateCornerTerraces(
					left, leftCell, right, rightCell, bottom, bottomCell
				);
				return;
			}
			TriangulateCornerTerracesCliff(
				bottom, bottomCell, left, leftCell, right, rightCell
			);
			return;
		}
		if (rightEdgeType == HexEdgeType.Slope) {
			if (leftEdgeType == HexEdgeType.Flat) {
				TriangulateCornerTerraces(
					right, rightCell, bottom, bottomCell, left, leftCell
				);
				return;
			}
		}

Как же нам это триангулировать? Эту задачу можно разделить на две части: нижнюю и верхнюю.

Нижняя часть

Нижняя часть имеет уступы слева и обрыв справа. Нам нужно их как-то объединить. Проще всего это сделать, сжав уступы, чтобы они встретились в правом углу. Это поднимет уступы вверх.

Сжатие уступов.

Но на самом деле мы не хотим, чтобы они встречались в правом углу, потому что это помешает уступам, которые могут существовать наверху. Кроме того, мы можем иметь дело с очень высоким обрывом, из-за которого получим очень резко опускающиеся и тонкие треугольники. Вместо этого мы сожмём их в граничную точку, которая лежит вдоль обрыва.

Сжатие на границе.

Давайте расположим граничную точку на один уровень выше нижней ячейки. Найти её можно интерполяцией на основании разности высот.

	void TriangulateCornerTerracesCliff (
		Vector3 begin, HexCell beginCell,
		Vector3 left, HexCell leftCell,
		Vector3 right, HexCell rightCell
	) {
		float b = 1f / (rightCell.Elevation - beginCell.Elevation);
		Vector3 boundary = Vector3.Lerp(begin, right, b);
		Color boundaryColor = Color.Lerp(beginCell.color, rightCell.color, b);
	}

Чтобы убедиться, что мы получили её правильно, покроем всю нижнюю часть одним треугольником.

		float b = 1f / (rightCell.Elevation - beginCell.Elevation);
		Vector3 boundary = Vector3.Lerp(begin, right, b);
		Color boundaryColor = Color.Lerp(beginCell.color, rightCell.color, b);

		AddTriangle(begin, left, boundary);
		AddTriangleColor(beginCell.color, leftCell.color, boundaryColor);

Нижний треугольник.

Разместив границу в нужном месте, мы можем перейти к триангуляции уступов. Давайте снова начнём только с первого этапа.

		float b = 1f / (rightCell.Elevation - beginCell.Elevation);
		Vector3 boundary = Vector3.Lerp(begin, right, b);
		Color boundaryColor = Color.Lerp(beginCell.color, rightCell.color, b);

		Vector3 v2 = HexMetrics.TerraceLerp(begin, left, 1);
		Color c2 = HexMetrics.TerraceLerp(beginCell.color, leftCell.color, 1);

		AddTriangle(begin, v2, boundary);
		AddTriangleColor(beginCell.color, c2, boundaryColor);

Первый этап сжатия.

На этот раз последний этап тоже будет треугольником.

		AddTriangle(begin, v2, boundary);
		AddTriangleColor(beginCell.color, c2, boundaryColor);

		AddTriangle(v2, left, boundary);
		AddTriangleColor(c2, leftCell.color, boundaryColor);

Последний этап сжатия.

И все промежуточные этапы тоже являются треугольниками.

		AddTriangle(begin, v2, boundary);
		AddTriangleColor(beginCell.color, c2, boundaryColor);

		for (int i = 2; i < HexMetrics.terraceSteps; i++) {
			Vector3 v1 = v2;
			Color c1 = c2;
			v2 = HexMetrics.TerraceLerp(begin, left, i);
			c2 = HexMetrics.TerraceLerp(beginCell.color, leftCell.color, i);
			AddTriangle(v1, v2, boundary);
			AddTriangleColor(c1, c2, boundaryColor);
		}

		AddTriangle(v2, left, boundary);
		AddTriangleColor(c2, leftCell.color, boundaryColor);

Сжатые уступы.

Завершение угла

Закончив нижнюю часть, можно перейти к верхней. Если верхнее ребро является склоном, то нам снова нужно будет соединить уступы и обрыв. Поэтому давайте переместим этот код в отдельный метод.

	void TriangulateCornerTerracesCliff (
		Vector3 begin, HexCell beginCell,
		Vector3 left, HexCell leftCell,
		Vector3 right, HexCell rightCell
	) {
		float b = 1f / (rightCell.Elevation - beginCell.Elevation);
		Vector3 boundary = Vector3.Lerp(begin, right, b);
		Color boundaryColor = Color.Lerp(beginCell.color, rightCell.color, b);

		TriangulateBoundaryTriangle(
			begin, beginCell, left, leftCell, boundary, boundaryColor
		);
	}

	void TriangulateBoundaryTriangle (
		Vector3 begin, HexCell beginCell,
		Vector3 left, HexCell leftCell,
		Vector3 boundary, Color boundaryColor
	) {
		Vector3 v2 = HexMetrics.TerraceLerp(begin, left, 1);
		Color c2 = HexMetrics.TerraceLerp(beginCell.color, leftCell.color, 1);

		AddTriangle(begin, v2, boundary);
		AddTriangleColor(beginCell.color, c2, boundaryColor);

		for (int i = 2; i < HexMetrics.terraceSteps; i++) {
			Vector3 v1 = v2;
			Color c1 = c2;
			v2 = HexMetrics.TerraceLerp(begin, left, i);
			c2 = HexMetrics.TerraceLerp(beginCell.color, leftCell.color, i);
			AddTriangle(v1, v2, boundary);
			AddTriangleColor(c1, c2, boundaryColor);
		}

		AddTriangle(v2, left, boundary);
		AddTriangleColor(c2, leftCell.color, boundaryColor);
	}

Теперь завершить верхнюю часть будет просто. Если у нас есть склон, то добавляем повёрнутый треугольник границы. В противном случае достаточно простого треугольника.

	void TriangulateCornerTerracesCliff (
		Vector3 begin, HexCell beginCell,
		Vector3 left, HexCell leftCell,
		Vector3 right, HexCell rightCell
	) {
		float b = 1f / (rightCell.Elevation - beginCell.Elevation);
		Vector3 boundary = Vector3.Lerp(begin, right, b);
		Color boundaryColor = Color.Lerp(beginCell.color, rightCell.color, b);
		
		TriangulateBoundaryTriangle(
			begin, beginCell, left, leftCell, boundary, boundaryColor
		);

		if (leftCell.GetEdgeType(rightCell) == HexEdgeType.Slope) {
			TriangulateBoundaryTriangle(
				left, leftCell, right, rightCell, boundary, boundaryColor
			);
		}
		else {
			AddTriangle(left, right, boundary);
			AddTriangleColor(leftCell.color, rightCell.color, boundaryColor);
		}
	}

Завершённая триангуляция обеих частей.

Зеркальные случаи

Мы рассмотрели случаи «склон-обрыв». Существуют ещё и два зеркальных случая, у каждого из которых слева есть обрыв.

ОСС и ОСО.

Мы воспользуемся предыдущим подходом, с небольшими отличиями из-за смены ориентации. Скопируем TriangulateCornerTerracesCliff и соответствующим образом его изменим.

	void TriangulateCornerCliffTerraces (
		Vector3 begin, HexCell beginCell,
		Vector3 left, HexCell leftCell,
		Vector3 right, HexCell rightCell
	) {
		float b = 1f / (leftCell.Elevation - beginCell.Elevation);
		Vector3 boundary = Vector3.Lerp(begin, left, b);
		Color boundaryColor = Color.Lerp(beginCell.color, leftCell.color, b);

		TriangulateBoundaryTriangle(
			right, rightCell, begin, beginCell, boundary, boundaryColor
		);

		if (leftCell.GetEdgeType(rightCell) == HexEdgeType.Slope) {
			TriangulateBoundaryTriangle(
				left, leftCell, right, rightCell, boundary, boundaryColor
			);
		}
		else {
			AddTriangle(left, right, boundary);
			AddTriangleColor(leftCell.color, rightCell.color, boundaryColor);
		}
	}

Добавим эти случаи в TriangulateCorner.

		if (leftEdgeType == HexEdgeType.Slope) {
			…
		}
		if (rightEdgeType == HexEdgeType.Slope) {
			if (leftEdgeType == HexEdgeType.Flat) {
				TriangulateCornerTerraces(
					right, rightCell, bottom, bottomCell, left, leftCell
				);
				return;
			}
			TriangulateCornerCliffTerraces(
				bottom, bottomCell, left, leftCell, right, rightCell
			);
			return;
		}

Триангулированные ОСС и ОСО.

Двойные обрывы

Единственными оставшимися неплоскими случаями являются нижние ячейки с обрывами по обеим сторонам. При этом верхнее ребро может быть любым — плоским, склоном или обрывом. Нас интересует только случай «обрыв-обрыв-склон», потому что у него единственного будут уступы.

На самом деле существует две разные версии «обрыв-обрыв-склон», в зависимости от того, какая сторона выше. Они являются зеркальными отражениями друг друга. Давайте обозначим их как ООСП и ООСЛ.

ООСП и ООСЛ.

Мы можем покрыть оба случая в TriangulateCorner, вызывая методы TriangulateCornerCliffTerraces и TriangulateCornerTerracesCliff с разными поворотами ячеек.

		if (leftEdgeType == HexEdgeType.Slope) {
			…
		}
		if (rightEdgeType == HexEdgeType.Slope) {
			…
		}
		if (leftCell.GetEdgeType(rightCell) == HexEdgeType.Slope) {
			if (leftCell.Elevation < rightCell.Elevation) {
				TriangulateCornerCliffTerraces(
					right, rightCell, bottom, bottomCell, left, leftCell
				);
			}
			else {
				TriangulateCornerTerracesCliff(
					left, leftCell, right, rightCell, bottom, bottomCell
				);
			}
			return;
		}

Однако при это создаётся странная триангуляция. Так происходит, потому что теперь мы триангулируем сверху вниз. Из-за этого наша граница интерполируется как отрицательная, что неверно. Решение здесь заключается в том, чтобы интерполяторы всегда были положительными.

	void TriangulateCornerTerracesCliff (
		Vector3 begin, HexCell beginCell,
		Vector3 left, HexCell leftCell,
		Vector3 right, HexCell rightCell
	) {
		float b = 1f / (rightCell.Elevation - beginCell.Elevation);
		if (b < 0) {
			b = -b;
		}
		…
	}

	void TriangulateCornerCliffTerraces (
		Vector3 begin, HexCell beginCell,
		Vector3 left, HexCell leftCell,
		Vector3 right, HexCell rightCell
	) {
		float b = 1f / (leftCell.Elevation - beginCell.Elevation);
		if (b < 0) {
			b = -b;
		}
		…
	}

Триангулированные ООСП и ООСЛ.

Подчистка

Мы рассмотрели все случаи, требующие особой обработки, чтобы обеспечить правильную триангуляцию уступов.

Завершённая триангуляция с уступами.

Мы можем немного очистить TriangulateCorner, избавившись от операторов return и использовав вместо них блоки else.

	void TriangulateCorner (
		Vector3 bottom, HexCell bottomCell,
		Vector3 left, HexCell leftCell,
		Vector3 right, HexCell rightCell
	) {
		HexEdgeType leftEdgeType = bottomCell.GetEdgeType(leftCell);
		HexEdgeType rightEdgeType = bottomCell.GetEdgeType(rightCell);

		if (leftEdgeType == HexEdgeType.Slope) {
			if (rightEdgeType == HexEdgeType.Slope) {
				TriangulateCornerTerraces(
					bottom, bottomCell, left, leftCell, right, rightCell
				);
			}
			else if (rightEdgeType == HexEdgeType.Flat) {
				TriangulateCornerTerraces(
					left, leftCell, right, rightCell, bottom, bottomCell
				);
			}
			else {
				TriangulateCornerTerracesCliff(
					bottom, bottomCell, left, leftCell, right, rightCell
				);
			}
		}
		else if (rightEdgeType == HexEdgeType.Slope) {
			if (leftEdgeType == HexEdgeType.Flat) {
				TriangulateCornerTerraces(
					right, rightCell, bottom, bottomCell, left, leftCell
				);
			}
			else {
				TriangulateCornerCliffTerraces(
					bottom, bottomCell, left, leftCell, right, rightCell
				);
			}
		}
		else if (leftCell.GetEdgeType(rightCell) == HexEdgeType.Slope) {
			if (leftCell.Elevation < rightCell.Elevation) {
				TriangulateCornerCliffTerraces(
					right, rightCell, bottom, bottomCell, left, leftCell
				);
			}
			else {
				TriangulateCornerTerracesCliff(
					left, leftCell, right, rightCell, bottom, bottomCell
				);
			}
		}
		else {
			AddTriangle(bottom, left, right);
			AddTriangleColor(bottomCell.color, leftCell.color, rightCell.color);
		}
	}

Последний блок else покрывает все оставшиеся случаи, которые ещё не покрыты ранее. Этими случаями являются ППП (плоскость-плоскость-плоскость), ООП, ОООР и ОООЛ. Все они покрываются одним треугольником.

Все уникальные случаи.

unitypackage

Автор: PatientZero

Источник