Сейчас популярна тема онлайн-образования: все слышали про Coursera, Udacity, EdX. Это отличные образовательные платформы, содержащие много полезных курсов. Но можно ли их сделать более интеллектуальными? Вообще исследования по интеллектуальным обучающим системам (intelligent tutoring systems) ведутся давно и у ученых есть что предложить программистам-практикам. В этой статье в научно-популярной форме рассматриваются результаты и выводы, полученные научным сообществом, по построению конкретного вида интеллектуальных обучающих систем. Затрагиваются вопросы построения подсистем проверки решений задач, моделей обучаемого, алгоритмов управления учебным процессом.
Введение
Широко распространены обучающие программы с тестами, содержащими вопросы с вариантами выбора ответа, в числе которых один правильный, а остальные неверные, содержащие типичные ошибки. Теоретическую основу для создания подобных систем в 50-х гг. XX века разработали известный психолог Б.Ф. Скиннер и исследователь Н.А. Кроудер. Предложенные ими концепции неоднократно подвергались критике. В частности, критики отмечали, что контролироваться должны не только ответы, но и пути, ведущие к ним. Ну действительно, ведь главная цель обучения – не зазубривание правильных ответов, а формирование рациональных приемов решения типичных задач изучаемого предмета. Поэтому научная мысль пошла по новому пути. Во-первых, ученые начали создавать обучающие программы, способные распознать не только конечный ответ, но и оценить ход рассуждений обучаемого при выполнении задания (см. часть 1 этой статьи). Во-вторых, ученые начали разрабатывать средства измерения характеристик обучаемых, важных для управления процессом обучения (так называемые «модели обучаемого», см. часть 2) и алгоритмы управления учебным процессом (см. часть 3).
1.«Следящие» интеллектуальные обучающие программы
Интересным и, возможно, наиболее перспективным видом интеллектуальных обучающих программ являются «следящие» интеллектуальные обучающие программы. «Следящими» называются обучающие программы, предназначенные для обучения естественно-научным предметам (таким, как математика или физика), способные
- оценить каждый шаг решения обучаемого как «правильный» или «неправильный»,
- предоставить подсказку, указывающую на то, что неправильно в только что введенном шаге решения или на то, что нужно будет делать дальше,
- поставить оценку за решение.
«Следящими» такие программы называются потому, что для проверки хода решения обучаемого на завершенность и правильность они сверяют шаги решения обучаемого с шагами имеющихся в них решений. Имеющиеся в них решения могут быть сгенерированы автоматически некоторым алгоритмом или внесены в базу данных преподавателем.
Пожалуй, наиболее известной и наиболее развитой «следящей» интеллектуальной обучающей программой является Andes Physics Tutor [1-2](рис. 1). Ее база знаний включает несколько разделов физики: «статика», «кинематика», «работа и энергия». Обучаемые вводят шаги решений в специальные поля. Если шаг решения правильный, программа подкрашивает соответствующую ему формулу в зеленый цвет, если неправильный – то в красный цвет. В нижней левой части окна программы отображаются полученные обучаемым подсказки.
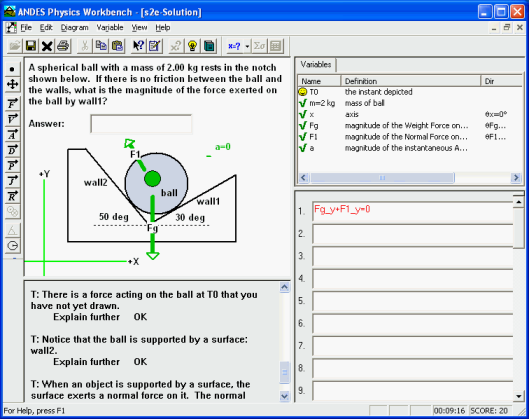
Рис. 1. «Следящая» интеллектуальная обучающая программа Andes Physics Tutor.
Как же реализована проверка решения в таких обучающих программах? Разработчики Andes Physics Tutor предлагают решать эту задачу в два этапа:
- проверка корректности введенной обучаемым формулы,
- измерение того, насколько далеко продвинулся обучаемый после ввода шага решения, т.е. измерение прогресса в решении.
Как раз именно на основании сведений о корректности введенные обучаемым формулы окрашиваются программой в красный или зеленый цвет. Сведения о прогрессе в решении задействуются программой в моменты формирования подсказок и выставления оценки за решение.
Проверку на корректность осуществлять очень просто: в формулу, введенную обучаемым, нужно подставить числовые значения содержащихся в ней переменных. Если в результате подстановки получается тождество, то формула корректна. Например, если обучаемый ввел формулу a = b + 2, а из условий задачи следует, что a = 4, b = 2, то, поскольку 4 = 2 + 2, то формула, введенная обучаемым, корректна.
Измерить прогресс в решении задачи значительно сложнее. Наиболее простой способ измерения прогресса в решении заключается в представлении известных программе решений задачи в виде списков формул и сравнения формул, введенных обучаемым, с формулами из этих списков. Тогда для измерения прогресса необходимо будет сначала выбрать одно из известных программе решений, наиболее близкое к решению обучаемого, а затем посмотреть, какой процент содержащихся в нем формул реализован в шагах решения обучаемого. Чем больше этот процент, тем больше прогресс в решении обучаемого. К сожалению, при использовании такого «наивного» способа хранения и обработки информации о решениях задач даже для самой простой задачи требуется внести слишком много возможных решений, отличающихся друг от друга одной или несколькими формулами. Поэтому разработчики Andes Physics Tutor пошли по другому пути.
В Andes Physics Tutor информация о возможных решениях задач хранится в виде небольшого списка «базовых» уравнений. Шаги решения, вводимые обучаемыми, тоже рассматриваются как уравнения. Для определения того, какие «базовые» уравнения использовались обучаемым для ввода того или иного шага решения, используется специальный алгоритм, в ходе работы которого выполняется решение систем уравнений и вычисление частных производных. Между тем, этот алгоритм способен справиться не со всеми шагами решения обучаемых. Чем больше в шаге решения обучаемого переменных заменено на числовые значения и чем более вычислительно свернутой она является, тем труднее понять, какие «базовые» уравнения использовал обучаемый при вводе шага решения.
Предположим, что в ходе решения задачи обучаемому нужно вычислить величину a, которая может быть найдена двумя способами: a = b + c, a = d/2. Если обучаемый просто введет a = 6, то, как понять, каким способом он воспользовался? К тому же, некоторые обучаемые могут «хитрить»: например, если они работают с обучающей программой в компьютерном классе и услышали от соседа, что a равно 6 и как-то зависит от b, то они, зная, что b = 2, могут ввести шаг решения вида a = 8 – b. В этом случае в результате работы алгоритма измерения прогресса все равно будет сделан вывод о том, что обучаемый ввел формулу, используя один из двух вышеуказанных способов. Конечно же, можно придумать эвристики, которые позволят прояснить ситуацию в ряде случаев, но не во всех. Поэтому, нельзя утверждать, что когда-либо алгоритмы проверки решений обучающих программ со 100% уверенностью смогут распознать любой шаг решения обучаемого. Скорее, возможно лишь добиться того, чтобы обучающие программы могли с высокой вероятностью правильно распознавать большинство шагов решений обучаемых для конкретных классов задач из некоторых естественно-научных дисциплин.
2.Модели обучаемого
Еще одним способом интеллектуализации обучающих программ является использование моделей обучаемого. Напомним, что моделью обучаемого могут называться средства для измерения характеристик обучаемого, важных для управления процессом обучения, а также результаты измерения этих характеристик. Модели обучаемых бывают двух видов:
- отражающие уровень знаний и умений обучаемого,
- характеризующие психическое состояние обучаемого во время выполнения заданий в обучающей программе.
Для характеризации уровня знаний и умений обучаемых чаще всего используют оверлейные модели. В случае оверлейной модели предполагается, что представление знания, которое имеет эксперт, совпадает с представлением обучаемого, за исключением того, что знания обучаемого менее полны (см. рис. 2). Экспертные знания делятся на простые и небольшие части. Обучаемый либо знает каждую конкретную часть, либо не знает (или знает до некоторой степени).
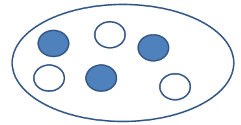
Рис. 2. Оверлейная модель обучаемого (закрашены те части «знаний» эксперта, которые присутствуют и у обучаемого).
В настоящее время оверлейные модели чаще всего реализуют в виде иерархических структур, включающих совокупность всех понятий рассматриваемого учебного курса и/или умений, соответствующих этому курсу. На рис. 3 представлена иерархическая структура понятий предмета «Геометрия», легшая в основу модели знаний и умений обучаемого. Узлы структуры соответствуют определениям, или аксиомам, или теоремам. Стрелка, ведущая от одного узла к другому, указывает на связь между порциями теоретического материала, соответствующими этим узлам. Эту связь можно интерпретировать так: «прежде чем изучать А, нужно знать B», или так: «если знает А, то знает и B». Учет связей между порциями теоретического материала позволяет уменьшить число упражнений, по результатам выполнения которых вычисляется уровень знаний и умений обучаемого.
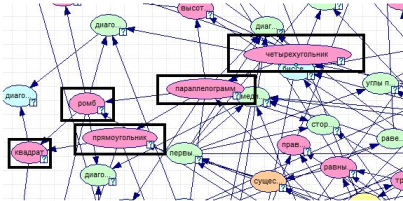
Рис. 3. Фрагмент иерархической структуры понятий из предметной области «Геометрия».
Каждому узлу структуры ставится в соответствие метка «выучено» или «не выучено». Смена метки может произойти после того, как обучаемый прочитает теоретический материал или выполнит практическое задание. Для расчетов, реализующих смену меток, могут применяться различные алгоритмы и методы: байесовские сети, методы нечеткой логики и т.д.
Для построения модели психического состояния обучаемого могут использоваться различные источники данных – видеокамеры (с их помощью распознается выражение лица), датчики, измеряющие пульс, и т.д. Незаметным для обучаемого источником получения данных и, соответственно, наиболее удобным для практического использования, является история работы пользователя в обучающей программе[3-4] (см. рис. 4).

Рис. 4. Фрагмент истории работы обучаемого.
В качестве примера модели диагностики психического состояния обучаемого по истории его работы опишем модель, разработанную в лаборатории 17 ИПУ РАН при участии сотрудников факультета психологии МГУ[5]. В этой модели предполагается, что психическое состояние обучаемого характеризуется значениями трех показателей: «Самостоятельность», «Усилия», «Фрустрационное поведение». Значения показателей пересчитываются каждые n секунд (например, можно взять n = 300 секунд, т.е. 5 минут). Значения показателей за некоторый период в основном формируются на основе различных численных характеристик различных событий, произошедших в течение этого периода. Эти события могут быть одномоментными (например, «обучаемый проверил шаг решения на правильность, шаг оказался правильным») или длительными (например, «обучаемый почитал справочный материал»). Численными характеристиками событий могут быть «количество», «средняя длительность», «совокупная длительность» и т.д.
При построении модели интересным событием в истории работы студента оказалось событие «бездействие в обучающей программе дольше 7 секунд». Оказалось, что появление этого события в истории работы обучаемого может говорить как о благоприятном для обучения состоянии обучаемого, так и о весьма нежелательном его состоянии. Чаще всего неблагоприятное состояние обучаемого проявлялось после того, как он вводил шаг решения задачи и получал сообщение от программы о его неправильности. В этом случае он прекращал работу в программе и пытался получить помощь у соседей или преподавателей или даже на некоторое время впадал в состояние ступора. Благоприятное состояние обучаемого проявлялось после того, как программа помечала введенный им шаг решения как правильный. Тогда он приступал к работе над следующим шагом решения и начинал вычисления с помощью бумаги и ручки (соответственно, в это время в программе не фиксировалось никаких действий обучаемого). Поэтому для измерения психического состояния обучаемого стали отдельно учитываться такие события, как «количество событий бездействия в программе дольше 7 секунд, которым предшествовал ввод правильного шага решения», и «количество событий бездействия дольше 7 секунд, которым предшествовал ввод неправильного шага решения».
Перед использованием модели необходимо ее настроить, то есть, подобрать коэффициенты функций, с помощью которых вычисляются текущие значения показателей «Самостоятельность», «Усилия», «Фрустрационное поведение». Не вдаваясь в подробности, отметим, что процесс подбора коэффициентов итеративен, а одним из основных шагов алгоритма подбора коэффициентов является минимизация функции ошибки, отражающей величину расхождений между экспертными оценками и оценками, которые были сформированы моделью с коэффициентами, полученными в результате предыдущей итерации на некоторой части экспериментальных данных.
Поясним процедуру сбора данных, на основе которых осуществлялась настройка вышеописанной модели. Для сбора данных был проведен эксперимент, в ходе которого студенты-добровольцы решали одну или две задачи в обучающей программе. После проведения эксперимента были собраны экспертные оценки. Эксперты оценивали психическое состояние студентов на основе видеозаписей, в которых одновременно была доступна как запись с экрана студента, так и запись лица студента. Каждые 5 мин проигрывание видеозаписи работы студента останавливалось – эксперт должен был ввести оценки состояния студента в специальные поля окна программы. Затем для каждого 5-минутного фрагмента истории работы каждого студента был сформирован вектор, одна компонента которого соответствовала экспертной оценке психического состояния студента за рассматриваемый период, а остальные компоненты – численным характеристикам событий из истории работы, произошедшим в течение рассматриваемого периода. На основе этих данных (совокупности векторов) и были подобраны коэффициенты модели – c помощью известных методов машинного обучения.
3.Управление учебным процессом с использованием моделей обучаемого
Теперь, когда мы узнали о различных видах моделей обучаемого и способах их построения, вернемся к вопросу интеллектуального управления обучением. Сразу же возникает вопрос, в какие моменты времени можно управлять процессом обучения и как можно воздействовать на обучаемого – пользователя программы? Во-первых, можно интеллектуально подбирать учебный материал (теорию и/или задачи для решения) для следующих уроков, учитывая знания и умения обучаемого, зафиксированные в соответствующей модели. Во-вторых, можно осуществлять интерактивную поддержку процесса решения задачи в обучающей программе. «Умный» алгоритм управления будет выбирать время появления и частоту таких действий обучающей программы, как:
- предоставление помощи (например, в виде кратких текстовых подсказок по следующему прогнозируемому шагу задачи или в виде ссылок на теоретический материал, который будет полезен при решении этой задачи),
- отказ в предоставлении помощи по запросу студента,
- рекомендация другого учебного материала взамен решаемой задачи (например, более простой задачи, если студент не может справиться с текущей задачей),
- рекомендация временного завершения работы в программе (как напоминание о необходимости периодического отдыха или констатирование того факта, что «студент сегодня не в форме»),
- показ различных мотивирующих сообщений (например, «ты уже почти решил эту задачу!»).
Но насколько «настойчивым» и «решительным» должен быть такой алгоритм? Для ответа на этот вопрос посмотрим на результаты исследований Бенедикта де Булея[6]. Бенедикт де Булей — английский профессор, под руководством которого было выполнено немало исследований по автоматизированному управлению эмоциями студентов во время работы в обучающей программе. Он и его коллеги обратили внимание на то, что студенты технических специальностей могут негативно относиться к автоматизированному управлению процессом обучения, особенно в тех случаях, когда они сталкиваются с отказом в предоставлении помощи. Некоторые из наиболее рассерженных поведением программы студентов, принимавших участие в экспериментах де Булея, даже говорили что-то типа «это просто программа и она должна делать именно то, что ей говорят!»
Как видим, успешность автоматизированного управления учебным процессом сильно зависит от степени веры обучаемого в интеллектуальность программы. Эта вера существенно зависит от того, насколько хорошо программа понимает его действия, в частности, что именно он ввел в тот или иной момент решения задачи в качестве шага решения. Как уже говорилось ранее, нельзя утверждать, что когда-либо алгоритмы проверки решений обучающих программ со 100% уверенностью смогут распознать любой шаг решения обучаемого. Поэтому алгоритм автоматизированного управления обучением должен лишь носить рекомендательный характер. Также должна существовать возможность его отключения по запросу обучаемого.
Между тем, в случаях нерационального поведения студентов (например, злоупотреблении студентами краткими текстовыми подсказками во время решения задач) все же можно влиять на процесс обучения, пускай и с привлечением дополнительных сил в лице преподавателя курса. Преподаватель может «штрафовать» студентов на основе автоматически сформированных отчетов об их поведении в обучающей программе. Таким образом, интеллектуальные обучающие программы могут существенно облегчить этот процесс как студенту, так и преподавателю, но в случае «хитрых» студентов с неправильной мотивацией (когда неинтересно изучать предмет, но интересно получать хорошие оценки) без участия преподавателя обойтись все равно будет невозможно.
Полезные ссылки
В качестве книги, в которой дан достаточно полный и относительно свежий обзор состояния исследований по интеллектуальным обучающим системам, рекомендую книгу Woolf, Beverly Park (2009). Building Intelligent Interactive Tutors. Morgan Kaufmann. ISBN 978-0-12-373594-2.
Практически ежегодно проходит конференция Intelligent Tutoring Systems. ITS 2010 была проведена в Питтсбурге (США), ITS 2012 — на Крите. Периодически проводит конференции общество AIED.
- Shapiro J.A. An Algebra Subsystem for Diagnosing Students' Input in a
Physics Tutoring System - VanLehn K. (et al.) The Andes Physics Tutoring System: Lessons Learned
- Baker R.S.J.d. (et al.) Towards Sensor-Free Affect Detection in
Cognitive Tutor Algebra - Baker R.S.J.d. (et al.) Labeling Student Behavior
Faster and More Precisely with Text Replays - Смирнова Н.В. Автоматизированный анализ психического состояния студентов по истории их работы в следящей интеллектуальной обучающей системе
- B. de Boulay, Soldato T. Implementation of motivational tactics in
tutoring systems
Автор: indrauolles