Кватернионы для чайников

В данной статье на конкретном примере рассматриваются особенности применения различных методов поворота 3D объекта в пространстве. В частности, сравнивается применение углов Эйлера и кватернионов.

Данная статья пригодится вам, если вы уже прочитали определение кватерниона и давно ищете наглядный материал для того, чтобы понять, зачем придумали кватернионы, и чем же они отличаются от углов Эйлера.

Наглядная демонстрация поворота по углам Эйлера уже была описана в статье на Хабре, особенно интересно поиграть с моделью самолётика (ссылки на программу в той же статье внизу).

Заручившись помощью чудесного сайта tinkercad.com представляю вам более наглядную демонстрацию поворотов предмета по углам Эйлера и сравнение с поворотом на основе кватерниона.

Демонстрация поворотов по углам Эйлера

Поворачивать будем избушку на курьих ножках. Вот ссылка на модель: Izba3D.

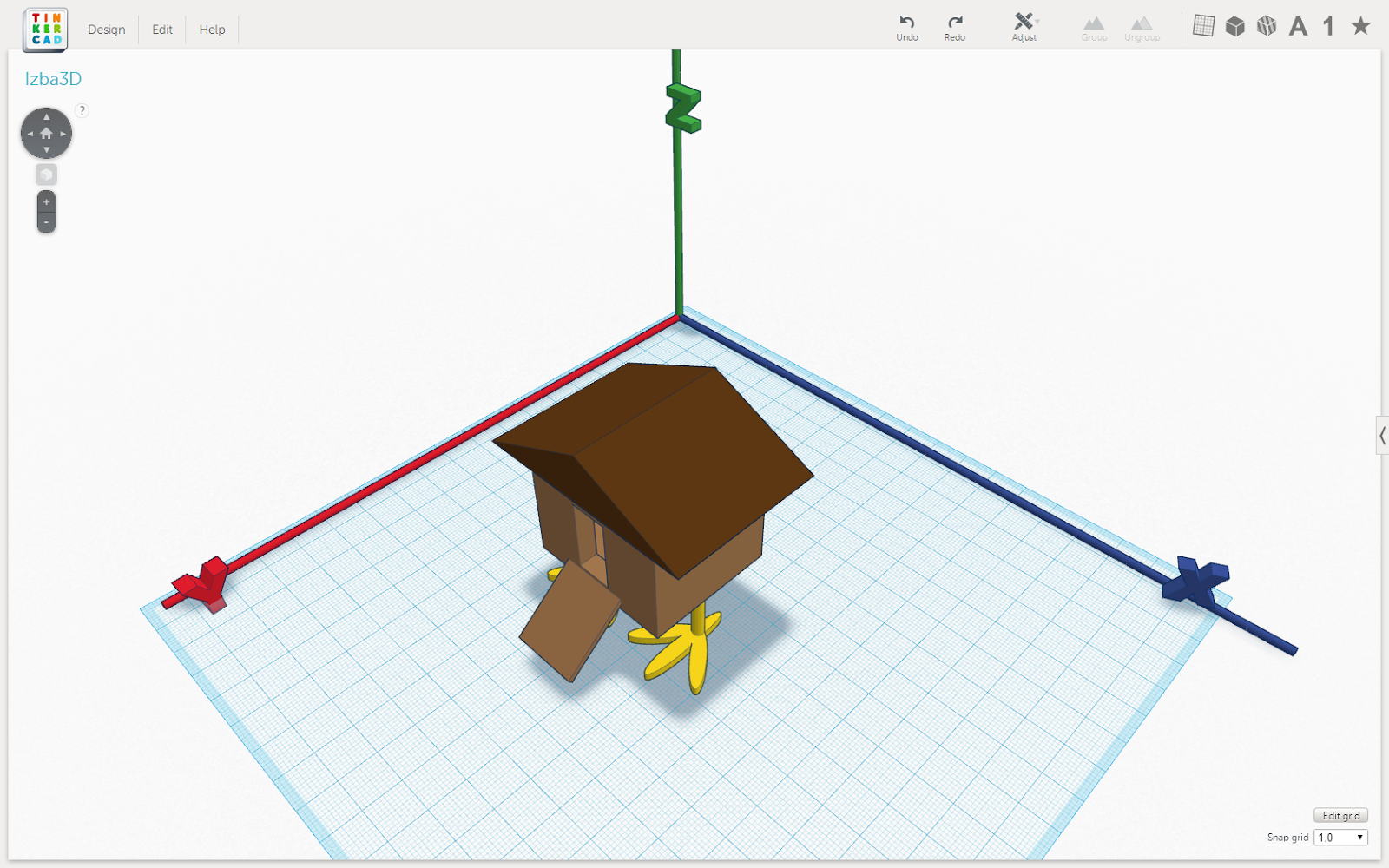
Рис. 1. Избушка в изометрии

Поворот вокруг оси Z, а потом оси Y

1. Повернуть на 90 градусов вокруг оси Z

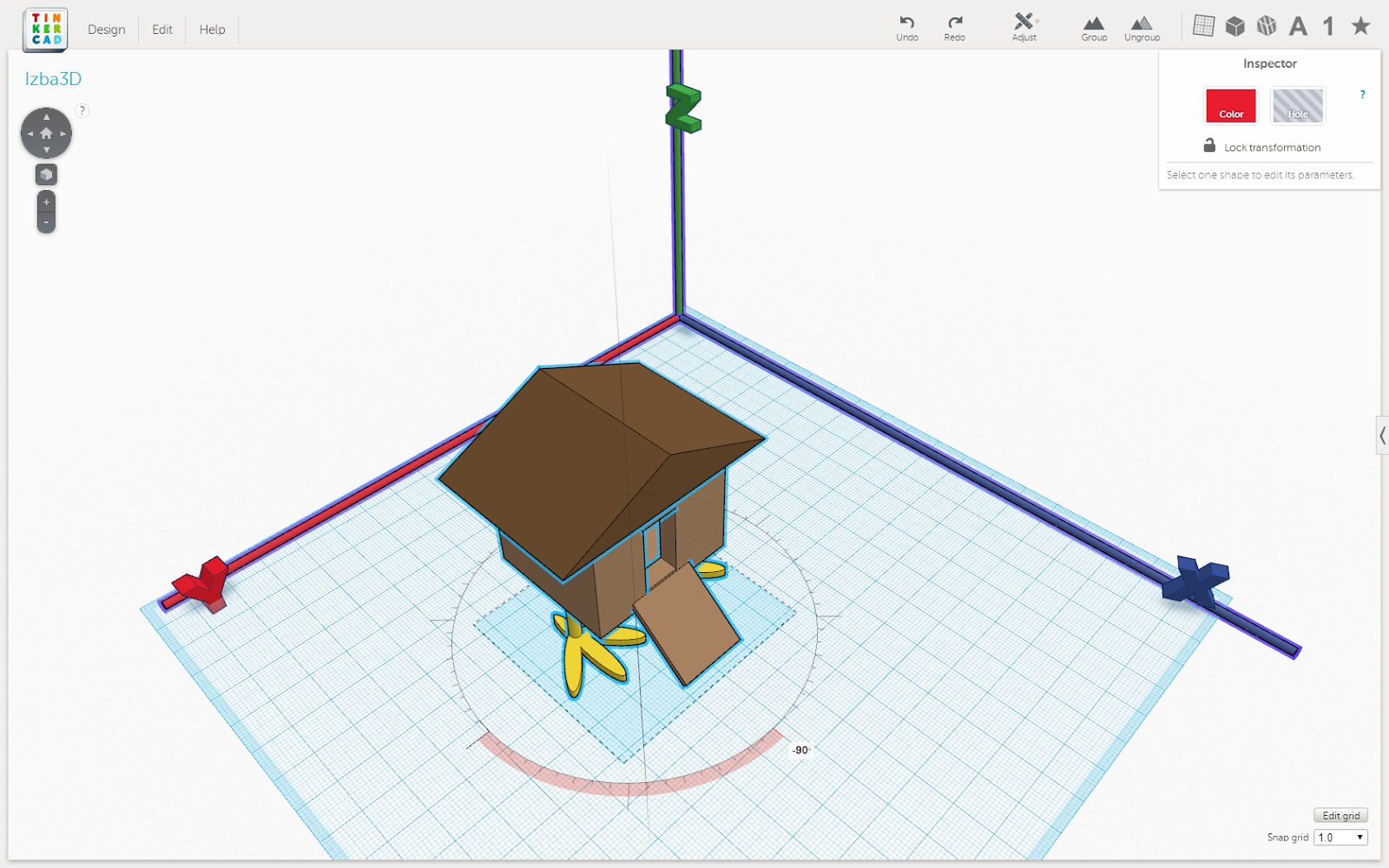
Рис. 2. Результат поворота рисунка 1 на 90 градусов вокруг оси Z

1. Повернуть на 90 градусов вокруг оси Y

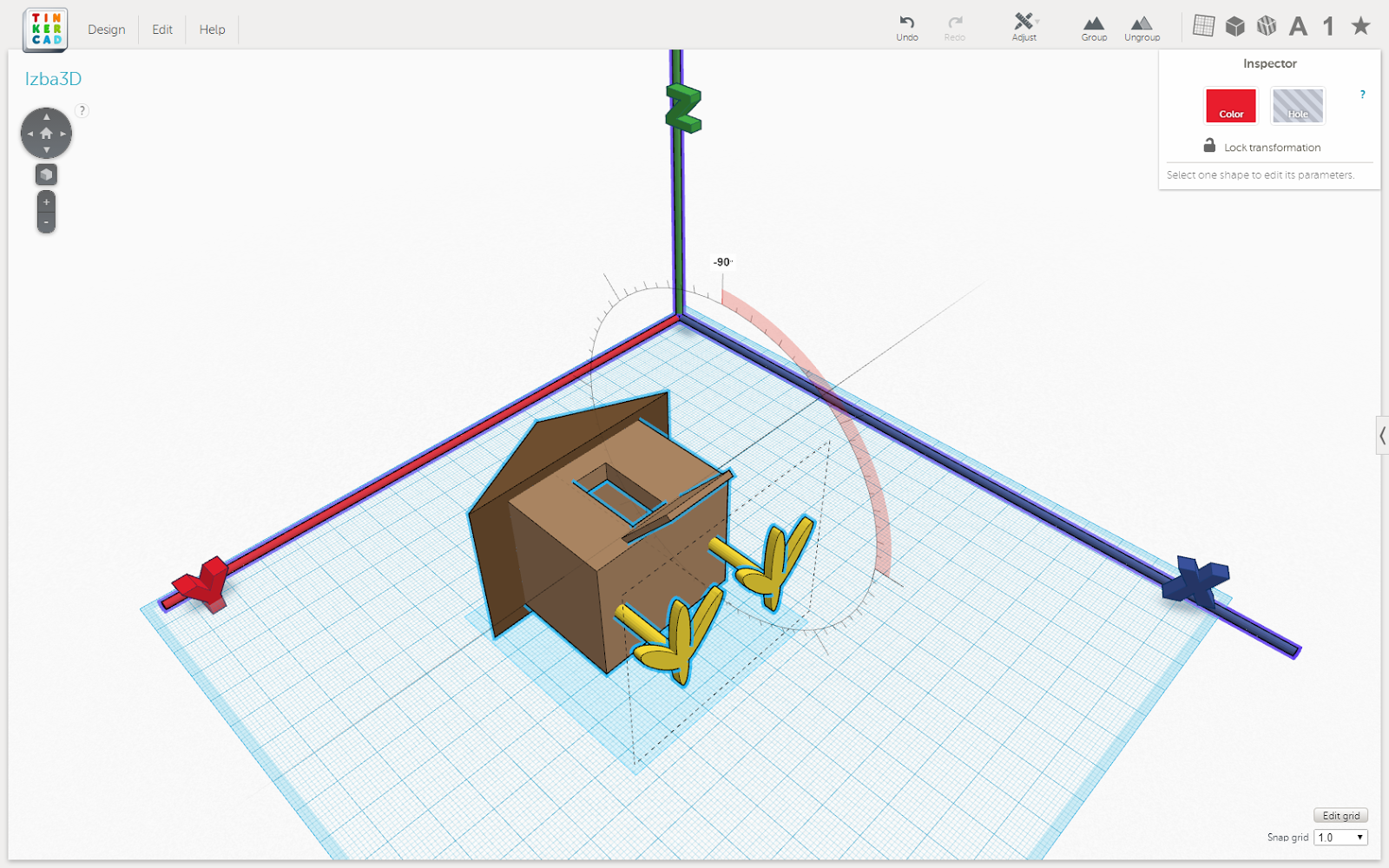
Рис. 3. Результат поворота рисунка 2 на 90 градусов вокруг оси Y

Поворот вокруг оси Y, а потом оси Z

1. Повернуть на 90 градусов вокруг оси Y

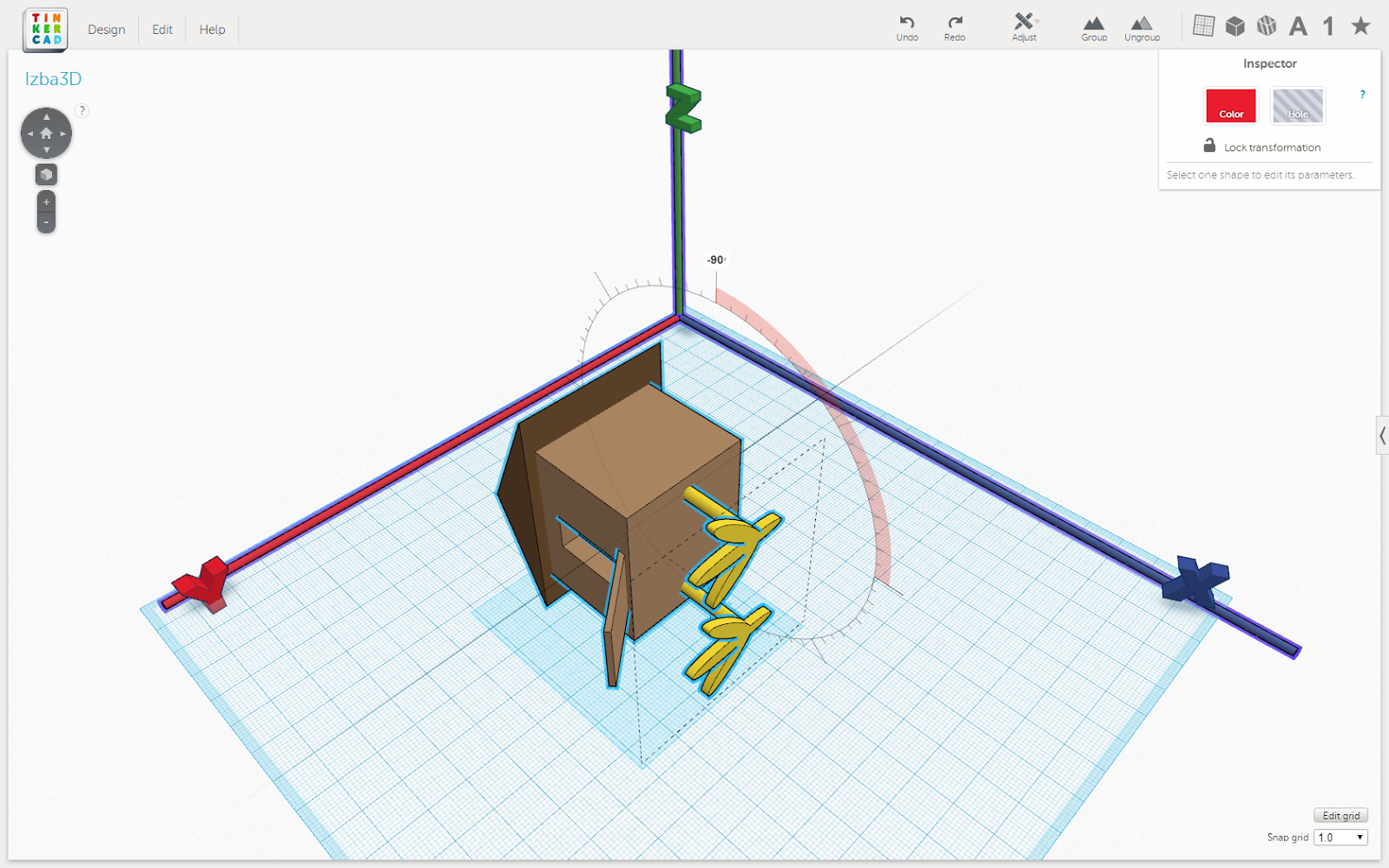
Рис. 4. Результат поворота рисунка 1 на 90 градусов вокруг оси Y

1. Повернуть на 90 градусов вокруг оси Z

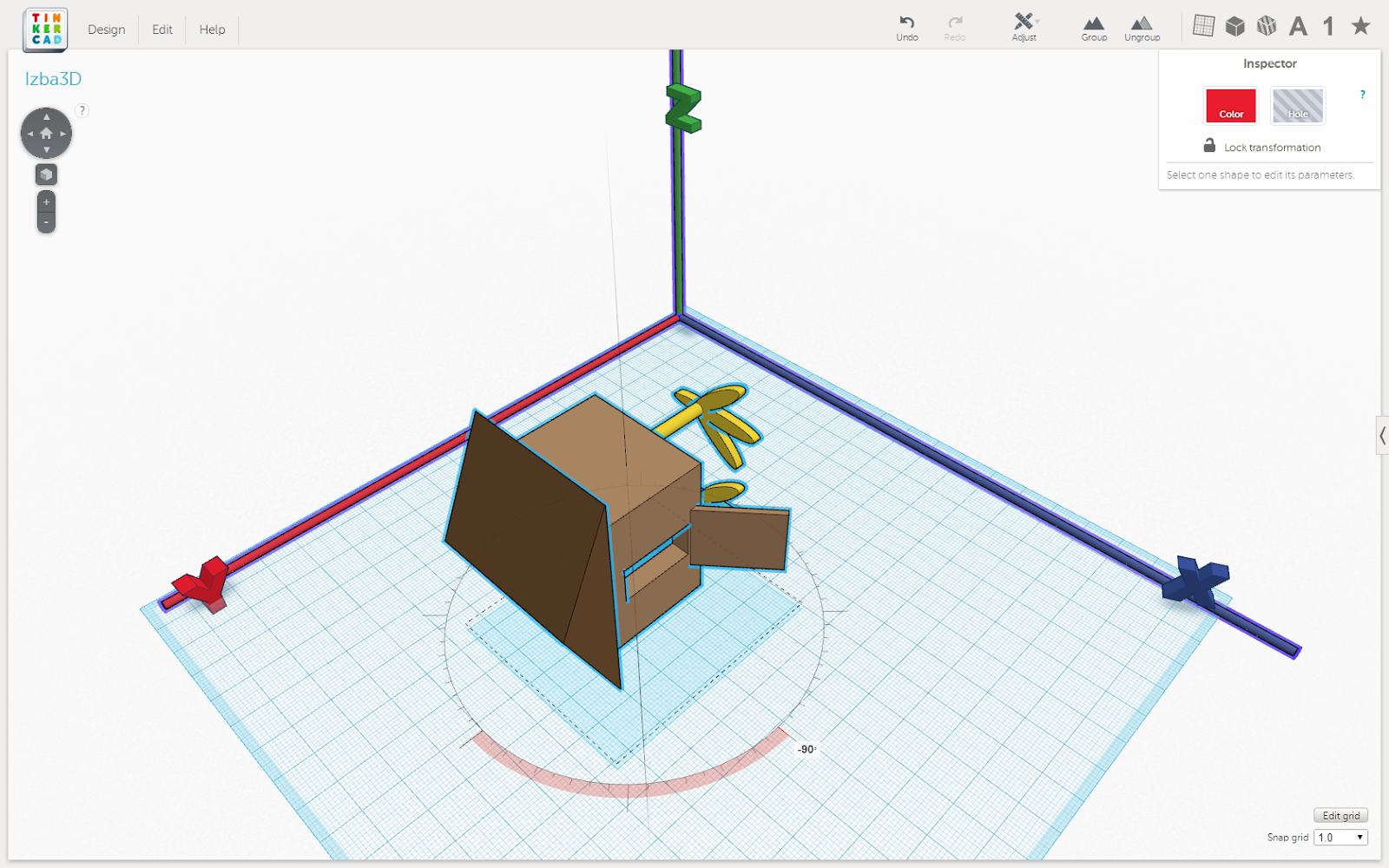
Рис. 5. Результат поворота рисунка 4 на 90 градусов вокруг оси Z

Сравнение и выводы

Сравним получившиеся картинки:

Рис. 6. Сравнение результатов поворота

Вывод: Порядок применения поворотов влияет на результат.

Кватернион

Гораздо удобнее пользоваться кватернионом, а именно, вектором и величиной поворота вокруг этого вектора.

Допустим, мы хотим повернуть избушку вокруг зелёного крылечка на 90, а потом снова на 90 градусов. Тогда пусть направление вектора совпадает с направлением зелёного крылечка.

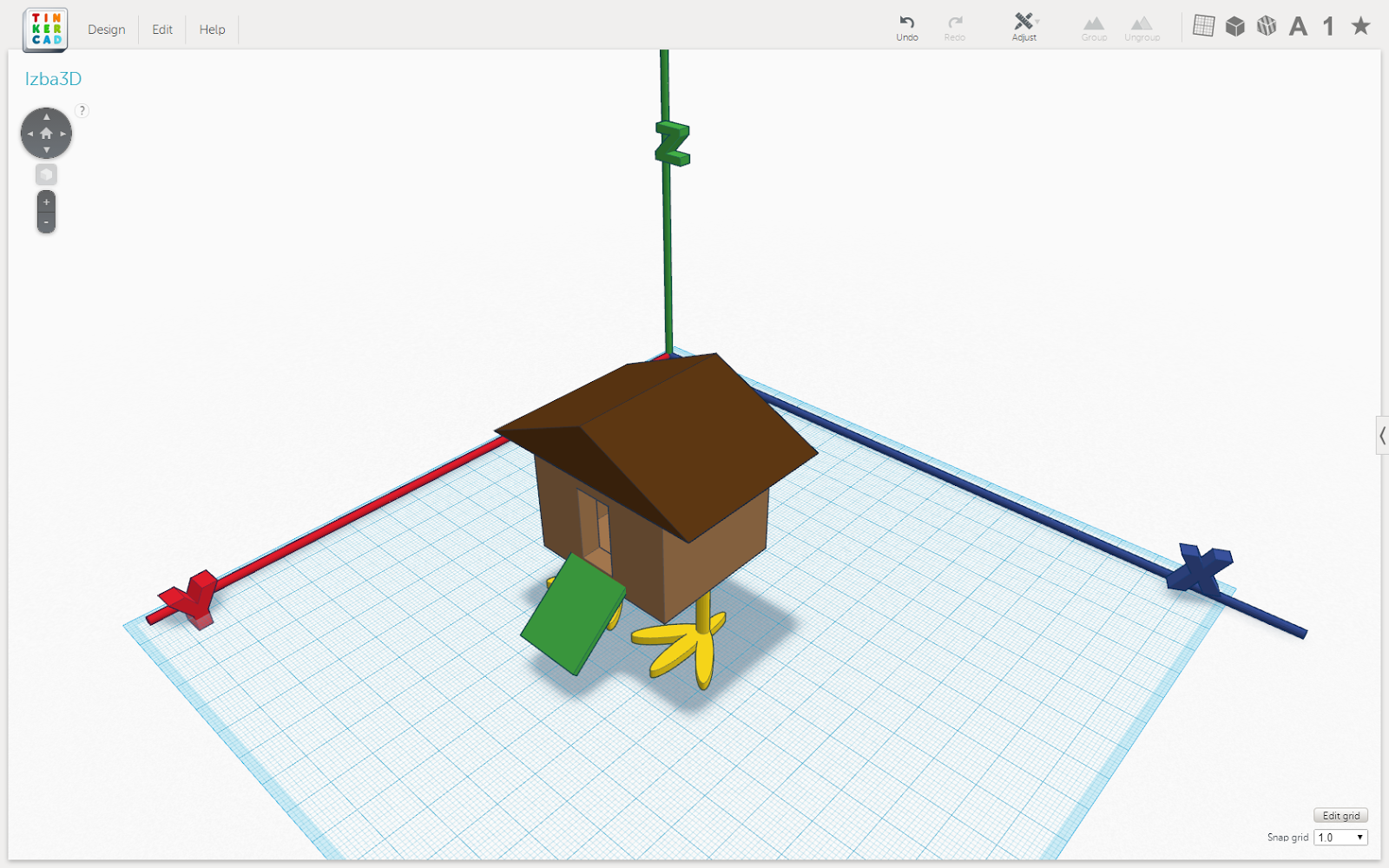
Рис. 7. Избушка на курьих ножках с зелёным крылечком

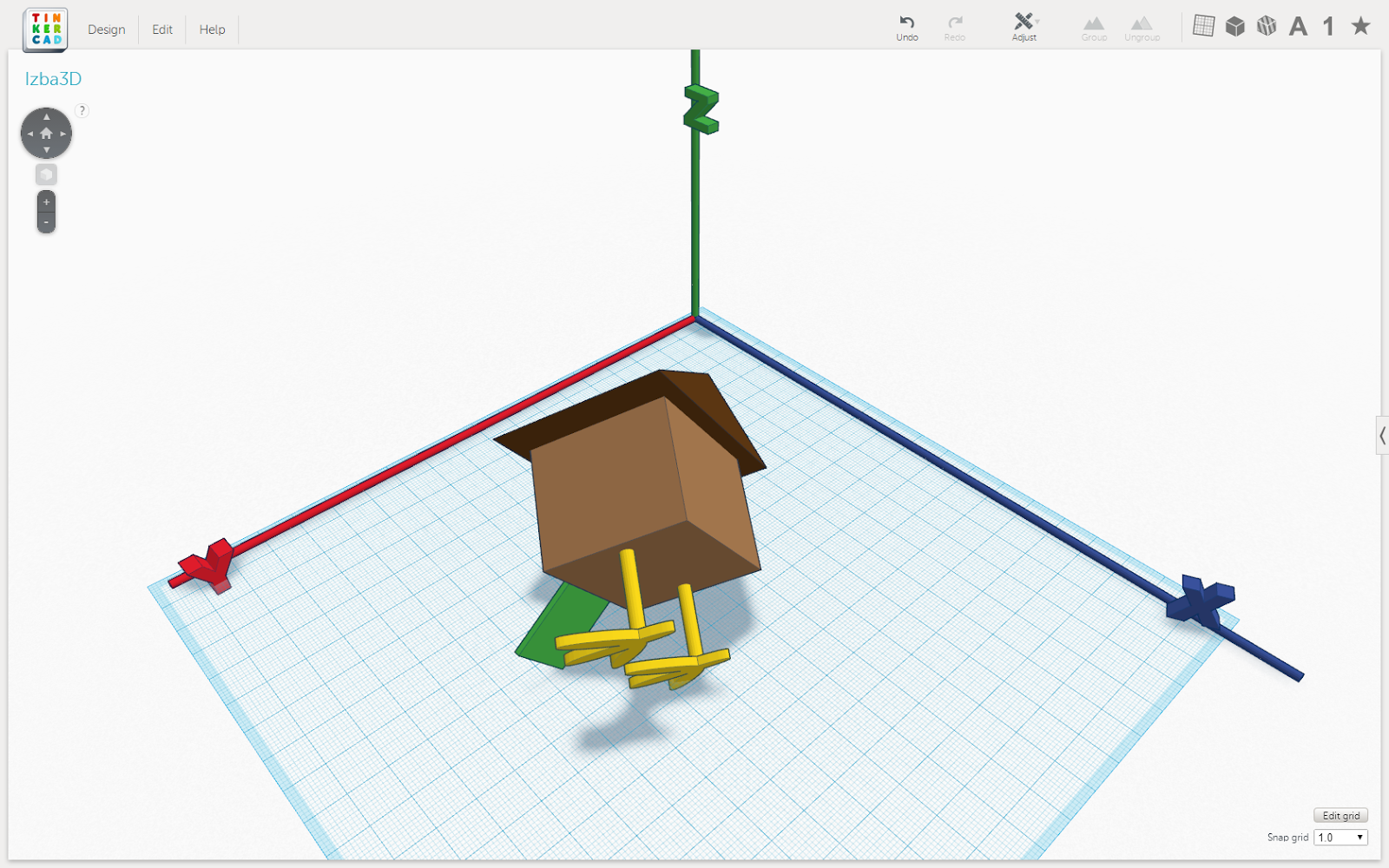
Рис. 8. Поворот на 90 градусов вокруг вектора, совпадающего с крылечком

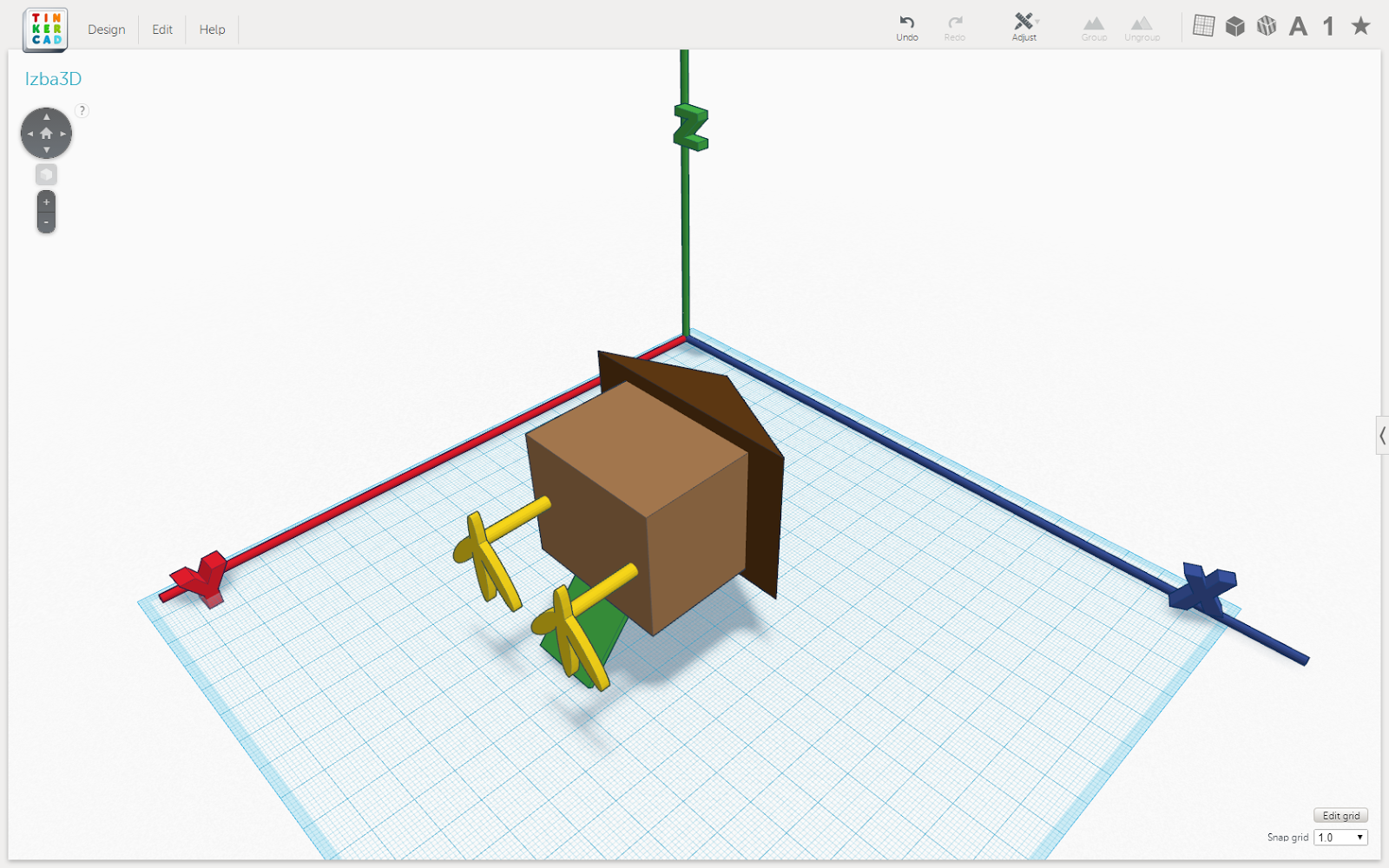
Рис. 9. Второй поворот на 90 градусов вокруг вектора, совпадающего с крылечком

Автор:

Источник