Опционы и формула Блэка-Шоулза (часть 1)

Часть 1

В этой серии статей я выведу уравнение Блека-Шоулза для оценки европейского call-опциона классическим способом.

DISCLAIMER: в этих статьях я пытаюсь дать интуицию что вообще происходит, поэтому во многих местах я специально опускаю математические формальности, чтобы не усложнять понимание.

В предыдущей статье обсуждалось, что такое опционы и как они работают. Теперь давайте выведем формулу для оценки стоимости европейского call-опциона.

Не пугайтесь всех терминов по ходу статьи, я буду стараться понятно пояснять каждый термин.

Небольшое отступление

В своём телеграм канале делюсь ещё больше полезным контентом по сфере деривативым и децентрализованных финансов: https://t.me/kirrya_achieves

Содержание статей (обе части)

1. Наивное представление движения цены на рынке

2. Добавляем случайности - движение цены как случайный процесс

3. Нормальное и лог-нормальное распределение

4. Уравнение движения цены, когда она распределена лог-нормально

5. Проблемы полученного уравнения

6. Теорема Гирсанова и риск-нейтральная мера

7. Избавились от неизвестного дрифта. Что дальше?

Наивное представление движения цены на рынке

Представим что у нас есть какой-нибудь рисковый актив, который торгуется на бирже. Например, стоимость эфира от времени.

Будем считать что мы ищем функцию, которая считает относительную стоимость (фактически наше S(t) это S(t)S0)

Мы хотим научиться делать какие-то предсказания по поводу будущей цены. В идеале хотелось бы иметь некоторую функцию S(t), которая в любой момент времени говорила бы сколько будет стоить базовый актив. Это можно записать в дифференциальной форме:

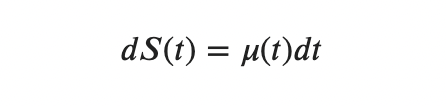
Интегрируя ее, мы получаем

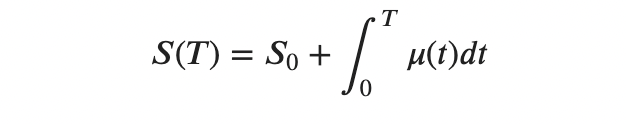
То есть такая функция, которая нам бы сказала будущую цену.

У такой модели есть проблема.

Мы видим только историю, и никто не знает куда пойдёт цена эфира в будущем. Она может пойти на сколько-то процентов вверх, может вниз, в общем - может быть всё что угодно. А мы бы хотели найти функцию, которая детерминированно говорит стоимость в будущем. Из-за кучи разных причин просто построить такую детерминированную функцию невозможно.

Добавляем случайности

Раз нельзя говорить однозначно о том, какая цена будет в будущем, рассмотрим процесс, в котором есть две части: детерминированная и стохастическая часть.

Нормальное и лог-нормальное распределение

Если рассматривать процесс, описанный выше, в любой момент времени величина X(t) будет распределена нормально (из-за добавки σdW, которая распределена нормально).

Но эмпирически замечено, что в реальности распределение цены на базовый актив не нормальное, а ближе к лог-нормальному. Это такое распределение, логарифм которого распределен нормально.

Это можно объяснить тем, что на рынках периодически случаются резкие обвалы, какие-то маловероятные события, которые обычно никто не принимает во внимание (у лог-нормального распределения "длинный хвост").

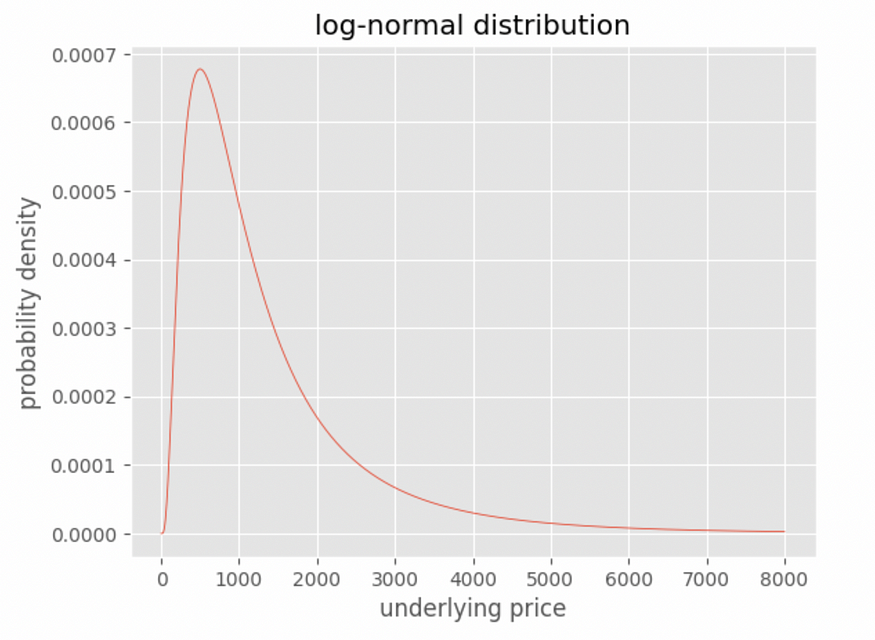
Лог-нормальноe распределениe в реальном мире (шутка)

Уравнение для движения цены, когда она распределена лог-нормально:

Мы изначально записали процесс, который распределен нормально:

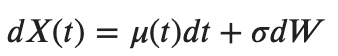
Возьмем логарифм от процесса X(t) и получим уравнение движения цены, распределение которой лог-нормальное:

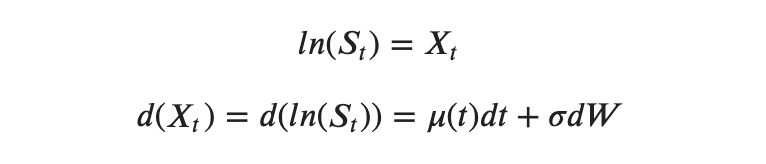
S_t — цена эфира на момент t

Помня, что

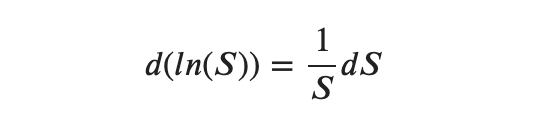
получаем

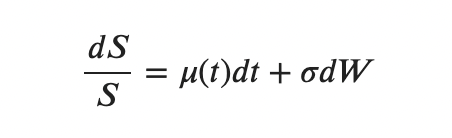
Наконец, мы получаем

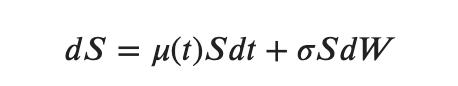
Это уравнение называется уравнением геометрического броуновского движения.

Мы хотим решить это уравнение, то есть получить функцию S(T)=... (она будет недетерминированной из-за стохастической части)

Проблемы текущего уравнения

Сейчас есть две проблемы:

1. Мы не знаем ничего о дрифте μ(t). Интуитивно это параметр "риска" для конкретной акции, монеты, токена (но формально параметр риска определяется иначе, в дальнейшем будет формула). И как бы этот параметр может быть в общем случае зависящем от времени.

2. Полученное уравнение решать довольно сложно. Нельзя просто взять и проинтегрировать, потому что в правой части стоят не константы, а функции μ(t)S и σS. Разделить переменные, перенеся S в левую часть и просто проинтегрировать тоже нельзя (немного позже увидим почему)

В следующих статьях мы преодолеем эти две проблемы.

В своём телеграм канале делюсь ещё больше полезным контентом по сфере деривативым и децентрализованных финансов: https://t.me/kirrya_achieves

Спасибо за ваше время.

Следите за обновлениями.