Привет, хабрапользователь! После небольшого перерыва можно опять браться за трехмерную графику. В этот раз мы поговорим о таком алгоритме глобального затенения, как Normal-oriented Hemisphere SSAO. Интересно? Под кат!

Но сначала чуть-чуть новостей
Я отказался от использования XNA, мощностей DX9 мне стало не хватать: конечно, в целом ничего не поменялось, но написание кода стало куда менее костыльным. Все последующие примеры будут реализованы с помощью фреймворка SharpDX.Toolkit: не пугайтесь, это духовный наследник XNA, еще и OpenSource и с поддержкой DX11.
Классически — теории.
Самой важной частью в графическом движке любой игры (которая имеет претензии на реалистичность) — это освещение. Сейчас невозможно полностью смоделировать освещение в игре real-time так, как это происходит в нашем, реальном мире. Условно говоря, не в real-time приложениях: освещение считается “пусканием” фотонов из источника света в нужных направлениях и регистрации этих фотонов камерой (глазом). Для подобных процессов в реальном времени требуется апромиксация, например: у нас есть некоторая поверхность и источник света, и для того что-бы создать освещение – требуется рассчитать “освещенность” каждого пикселя принадлежащей поверхности, т.е. учитывается только прямое влияние источника света на тексель. В данной апромиксации не учитывается непрямое освещение, т.е. в случае с real-time фотон может отразиться от какой-либо поверхности и повлиять на совершено другой “тексель”. Для единичных, небольших источников света это не особо критично, но стоит взять большой источник света и “бесконечно удаленный”, например, солнце (небо выступает как мощный «рассеиватель» света от солнца), то сразу возникают проблемы, примерно такие:

В реальном же мире, на подобной сцене не было бы такой черной черноты в местах теней. Развивая дальше тему, можно ввести некоторое значение ambient, которое будет отображать общую освещенность всей сцены, своеобразная аппроксимация непрямого освещения. Но дело в том, что подобное освещение на всей сцене везде одинаково, даже в тех местах, где непрямой свет будет оказывать наименьшее влияние. Но и тут можно схитрить и усложнить апромиксацию путем затенения тех участков, куда отраженному свету сложнее всего добраться. Таким образом мы подошли к понятию называемым “глобальное затенение” (ambient occlusion). Суть такого подхода заключается в том, что мы для каждого фрагменты сцены находим некоторый заграждающий фактор, т.е. кол-во не загражденных направлений падения “фотона” деленное на общее кол-во всевозможных направлений.
Рассмотрим следующую картинку:
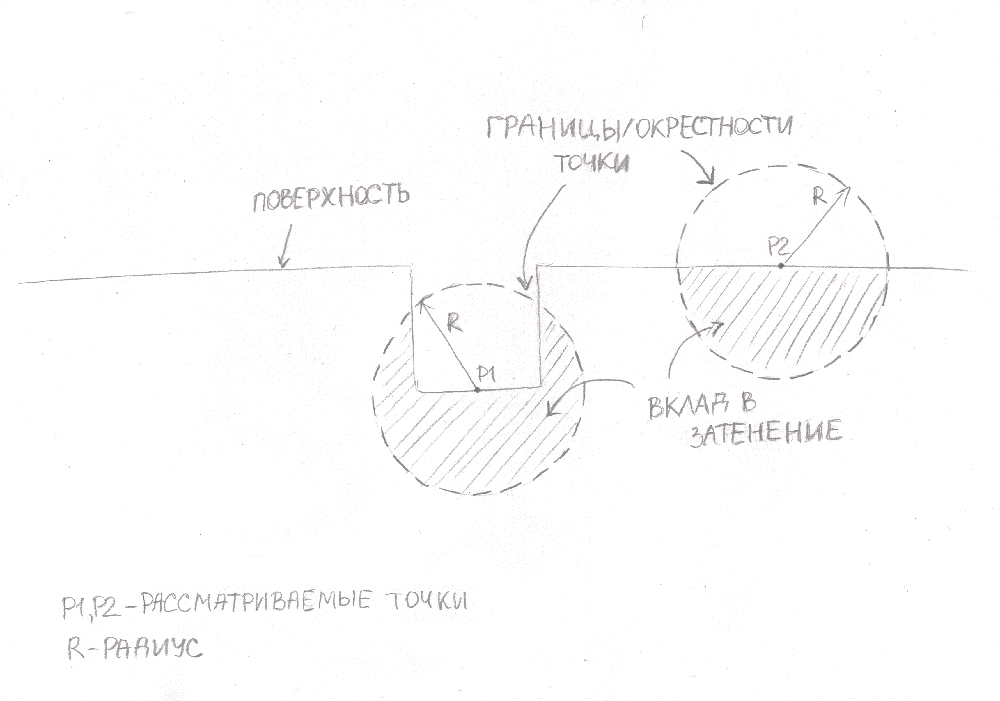
Тут у нас есть две рассматриваемые точки, которые образуют вокруг себя окружность с радиусом R. И для того, чтобы определить степень загражденности взятого фрагмента достаточно найти площадь незагражденного пространства и разделить на общую площадь окружности. Если мы подобную операцию проделаем для всех точек сцены – мы получим глобальное затенение. Выглядеть оно будет примерно так (для трехмерного случая):

Но теперь нужно подумать, как подобный алгоритм внедрить в пайп-лайн рендера графического конвейера. Сложность возникает в том, что отрисовка геометрии происходит постепенно. В следствии чего, первый объект в сцене не будет знать о существовании других. Можно, конечно, заранее рассчитать AO (на этапе загрузки) для сцены, но в таком случае мы не будем учитывать динамически изменяемую геометрию: физические объекты, персонажей, etc. И тут на помощь приходит работа с геометрией в экранном пространстве (Screen Space). Я его уже упоминал, когда рассказывал об SSLR-алгоритме. Этим можно воспользоваться и считать AO в экранном пространстве. Тут появляется самая классическая реализация SSAO, придумали его классные ребята из крайтек ровно 8 лет назад. Их алгоритм заключался в следующем: после рисования всей геометрии у них был в наличии буфер глубины, который несет в себе информацию об всей видимой геометрии, строя сферы для каждого текселя они считали кол-во затенения для сцены:

Тут, кстати, возникает еще одна сложность. Дело в том, что мы не можем учесть абсолютно все направления в real-time, во первых, потому, что пространство дискретно, а во вторых на производительности можно ставить крест. Мы не можем учесть даже 250 направлений (а именно столько необходимо для минимально-вменяемого качества изображения). Для того, чтобы сократить кол-во выборок – используют некоторое ядро направлений (от 8 до 32), которое вращают каждый раз на случайное значение. После этих операций нам доступен AO в реал-тайме:

Самое тяжелое в алгоритме SSAO это определение заграждения, ведь это чтение из float-текстуры.
Чуть позже была придумана модификация алгоритма SSAO: Normal-oriented Hemisphere SSAO. Суть модификации в том, что мы можем увеличить точность алгоритма за счет учета нормалей (по сути нужен GBuffer). Для пространства выборок мы будем использовать не сферу, а полусферу, которая ориентирована по нормали текущего текселя. Такой подход позволяет увеличить кол-во полезный выборок в двое.

Если посмотреть на рисунок, то можно понять, о чем я говорю:
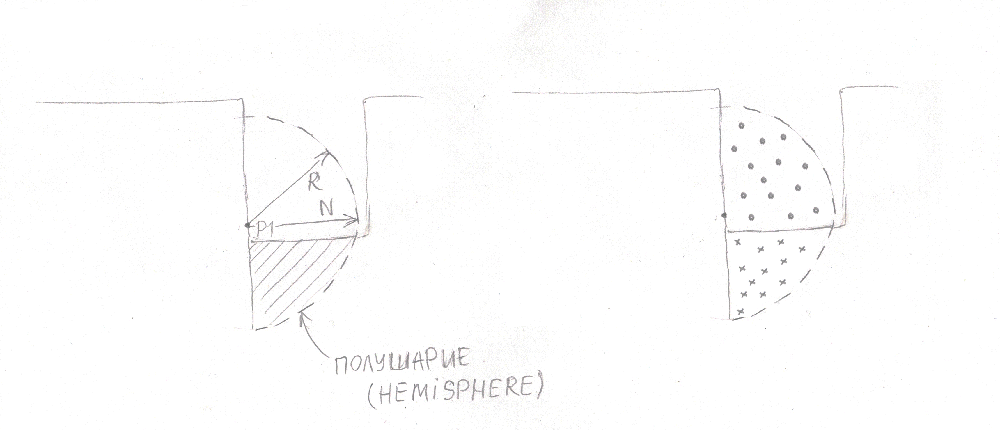
Завершающим этапом алгоритма будет размытие изображения AO для того, чтобы убрать шум, вызванным случайными выборками. В конечном счете – реализация нашего алгоритма будет выглядеть так:

С теорией пока все ясно, можно перейти к практике.
Зона свободная от теории
Советую прочитать эту статью, там я рассказывал про суть работы Screen Space пространством. Но, а в практике я приведу особо важные участки кода с нужными комментариями.
Самое первое, что нам понадобится, это информация о геометрии: GBuffer. Т.к. его построение не входит в тему статьи – о нем подробно расскажу как-нибудь в другой раз.
Второе — это полусфера со случайными направлениями:
_samplesKernel = new Vector3[128];
for (int i = 0; i < _samplesKernel.Length; i++)
{
_samplesKernel[i].X = random.NextFloat(-1f, 1f);
_samplesKernel[i].Z = random.NextFloat(-1f, 1f);
_samplesKernel[i].Y = random.NextFloat(0f, 1f);
_samplesKernel[i].Normalize();
float scale = (float)i / (float)_samplesKernel.Length;
scale = MathUtil.Lerp(0.1f, 1.0f, scale * scale);
_samplesKernel[i] *= scale;
}Тут важно отметить, что в шейдере у нас не будет трассировки, т.к. мы сильно ограничены в инструкциях, взамен этому – мы будем считать факт нахождения конечной точки в какой-либо геометрии, поэтому необходимо учитывать больше ближней геометрии, чем дальней. Для этого достаточно взять набор точек с нормальным распределением в полусфере. Это можно получить честным нормальным распределением, можно просто дважды умножить вектор на случайное число от 0 до 1, а можно воспользоваться небольшим хаком: задавать длину какой-либо функцией, например квадратичной. Это нам даст более лучший “сорт” ядра.
Третье – это набор каких-нибудь случайных векторов, для того, чтобы разнообразить конечные выборки, у меня оно генерируется в случайным образом:
Color[] randomNormal = new Color[_randomNormalTexture.Width * _randomNormalTexture.Height];
for (int i = 0; i < randomNormal.Length; i++)
{
Vector3 tsRandomNormal = new Vector3(random.NextFloat(0f, 1f), 1f, random.NextFloat(0f, 1f));
tsRandomNormal.Normalize();
randomNormal[i] = new Color(tsRandomNormal, 1f);
}Но выглядит оно примерно так:
Не стоит использовать подобную текстуру больше чем 4x4-8x8, потому, что подобное вращение ядра дает низкочастотный шум, который размыть в будущем куда проще.
Теперь поглядим на тело шейдера SSAO:
float depth = GetDepth(UV);
float3 texelNormal = GetNormal(UV);
float3 texelPosition = GetPosition2(UV, depth) + texelNormal * NORMAL_BIAS;
float3 random = normalize(RandomTexture.Sample(NoiseSampler, UV * RNTextureSize).xyz);
float ssao = 0;
[unroll]
for(int i = 0; i < MAX_SAMPLE_COUNT; i++)
{
float3 hemisphereRandomNormal = reflect(SamplesKernel[i], random);
float3 hemisphereNormalOrientated = hemisphereRandomNormal * sign(
dot(hemisphereRandomNormal, texelNormal));
ssao += calculateOcclusion(texelPosition,
texelNormal,
hemisphereNormalOrientated,
RADIUS);
}
return (ssao / MAX_SAMPLE_COUNT);Тут мы получаем нелинейную глубину, получаем мировую позицию и нормаль, получаем набор случайных векторов растянутых на весь экран. Стоит сразу заранее сказать про два хака.
Первый заключается в том, что мы сдвигаем позицию текселя на нормаль умноженную на некоторое маленькое значение, это необходимо для того, чтобы избавится от ненужных пересечений из-за дискретности screen space пространства:
А второй заключается в том, что в алгоритме нам необходимо сравнивать значения глубины, а нелинейная глубина на средних-дальних дистанциях находится в окрестностях единицы. По-хорошему мы должны эту глубину линеализировать, но т.к. подобные значения используются только для сравнения – можно ввести некоторое оценку нелинейной глубины:
float depthAssessment_invsqrt(float nonLinearDepth)
{
return 1 / sqrt(1.0 - nonLinearDepth);
}Отдельно стоит сказать, что хорошо бы сделать unroll-цикла, т.к. кол-во выборок заранее известно, подобный код будет работать быстрее.
Дальше начинается сам алгоритм:
Вращаем ядро и ориентируем это ядро по нормали в текстеле:
float3 hemisphereRandomNormal = reflect(SamplesKernel[i], random);
float3 hemisphereNormalOrientated = hemisphereRandomNormal * sign(
dot(hemisphereRandomNormal, texelNormal));И передаем функции расчета заграждения:
float calculateOcclusion(float3 texelPosition, float3 texelNormal, float3 sampleDir, float radius)
{
float3 position = texelPosition + sampleDir * radius;
float3 sampleProjected = GetUV(position);
float sampleRealDepth = GetDepth(sampleProjected.xy);
float assessProjected = depthAssessment_invsqrt(sampleProjected.z);
float assessReaded = depthAssessment_invsqrt(sampleRealDepth);
float differnce = (assessReaded - assessProjected);
float occlussion = step(differnce, 0); // (x >= y) ? 1 : 0
float distanceCheck = min(1.0, radius / abs(assessmentDepth - assessReaded));
return occlussion * distanceCheck;
}Берем сэмпл и проектируем его в экранное пространство (получаем новые значения UV.xy и нелинейную глубину):
float3 position = texelPosition + sampleDir * radius;
float3 sampleProjected = GetUV(position);Функция проекции выглядит следующим образом:
float3 _innerGetUV(float3 position, float4x4 VP)
{
float4 pVP = mul(float4(position, 1.0f), VP);
pVP.xy = float2(0.5f, 0.5f) + float2(0.5f, -0.5f) * pVP.xy / pVP.w;
return float3(pVP.xy, pVP.z / pVP.w);
}
float3 GetUV(float3 position)
{
return _innerGetUV(position, ViewProjection);
}
Константы 0.5f напрашиваются, чтобы их зашили в матричку.
После этого мы получаем новое значение глубины:
float assessProjected = depthAssessment_invsqrt(sampleProjected.z);
float assessReaded = depthAssessment_invsqrt(sampleRealDepth);
float differnce = (assessReaded - assessProjected);
float occlussion = step(differnce, 0); // (x >= y) ? 1 : 0Факт заграждения мы определяем как: “видна ли точка наблюдателю”, т.е. если точка не лежит в какой-либо геометрии – то assessReaded будет всегда строго меньше assessProjected.
Ну и с учетом того, что в экранном пространстве полно такого явления как information lost, мы должны регулировать кол-во затенения в зависимости от дистанции “проникновения” в геометрию. Это необходимо для того, что мы ничего не знаем о геометрии за видимой частью экранного пространства:
float distanceCheck = min(1.0, radius / abs(differnce));Ну и финальный этап, это размытие. Я лишь скажу то, что нельзя размывать буффер SSAO без учета неоднородности глубины как это делают многие. Так же, хорошо бы учесть и нормали при размытии, примерно так:
[flatten]
if(DepthAnalysis)
{
float lDepthR = LinearizeDepth(GetDepth(UVR));
float lDepthL = LinearizeDepth(GetDepth(UVL));
depthFactorR = saturate(1.0f / (abs(lDepthR - lDepthC) / DepthAnalysisFactor));
depthFactorL = saturate(1.0f / (abs(lDepthL - lDepthC) / DepthAnalysisFactor));
}
[flatten]
if(NormalAnalysis)
{
float3 normalR = GetNormal(UVR);
float3 normalL = GetNormal(UVL);
normalFactorL = saturate(max(0.0f, dot(normalC, normalL)));
normalFactorR = saturate(max(0.0f, dot(normalC, normalR)));
}Коэффициенты depthFactor и normalFactor учитываются в коэффициентах размытия.
Взамен заключения
Для более подробного изучения – я оставлю полный исходный код тут, а для любителей увидеть своим глазом демо тут.
Кстати, в демо я намерено оставил NORMAL_BIAS равным нулю, чтобы увидеть проблему, кроме того, в GBuffer рисуется только геометрия и нет normal-маппинга, из-за чего на дальних дистанциях происходит z-fighting.
В будущих статьях постараюсь осветить другие алгоритмы real-time ao, такие как HBAO, HDAO, HBAO+, если будет интересен к этой теме, конечно.
Удачной работы! ;)
Автор: ForhaxeD