Причин написания этой статьи две. Первая — показать, как можно использовать виды покрытия графов в тестировании, и привести еще один пример практического применения техники тестирования состояний и переходов. Вторая — пусть не опровергнуть, но хотя бы пошатнуть миф о том, что тестировщику не нужна математика и .
В сети есть довольно много материалов, описывающих процесс тестирования инсталлятора и результат его работы. Существует множество чеклистов и других полезностей на эту тему. Речь ниже пойдет о достаточно узкой части процесса инсталляции — тестировании собственно визарда. Достаточно ли пройтись по всем экранам визарда, чтобы утверждать, что он хорошо работает? Возможно, хватит нажать на каждую из кнопок «Назад», «Далее», «Отмена» по одному разу? Как ограничить количество сценариев, если оно бесконечно (можно сколько угодно раз перемещаться между двумя соседними экранами инсталлятора с помощью кнопок «Назад» и «Далее»)?
Для иллюстрации используется инсталлятор LibreOffice 5 под Windows. Решение взять именно его связано с доступностью подробных пошаговых скриншотов. В статье используется нотация из первой и второй статей о покрытии графов.
Составление графа состояний и переходов
Первое, что нужно сделать — выделить состояния. Это достаточно просто: как минимум, нужно взять в качестве состояния каждый шаг инсталлятора. Но вообще говоря, этого недостаточно для проверки визарда. Практически на каждом шаге можно вносить какие-то изменения, что порождает дополнительное состояние для каждого экрана, где это возможно. Внесение изменений важно, поскольку при возврате на предыдущие экраны они должны сохраняться.
Необходимость сохранения изменений также нужно учитывать и в переходах, т.е. возвращаться нужно не в исходное, а в измененное состояние. При построении графа я учитываю, что сценарии без изменений включаются в сценарии с изменениями в том смысле, что исходный и измененный экраны могут быть одинаковы. Таким образом, стандартный набор переходов для внутреннего экрана инсталлятора будет выглядеть так:
назад
|
экран -> измененный экран -> вперед
Кроме этого необходимо выделить конечные состояния. Для визарда их два: установка отменена и установка завершена. Для простоты в графе не учитывается аварийное прерывание процесса установки.
В визарде есть такие экраны:
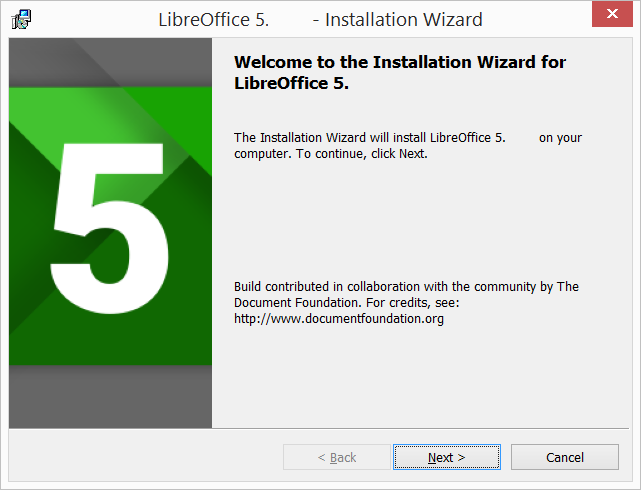
Соответствует состоянию «Welcome»
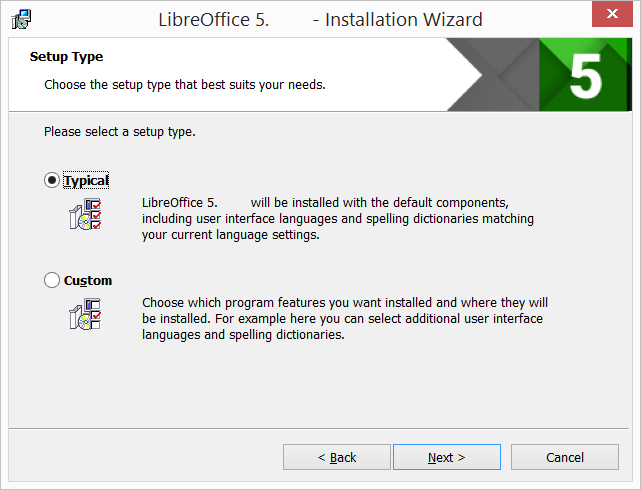
Соответствует состоянию «Setup Type»
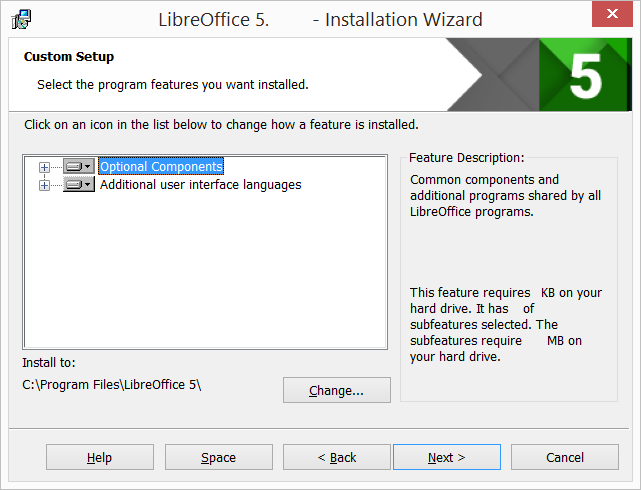
Соответствует состоянию «Custom»
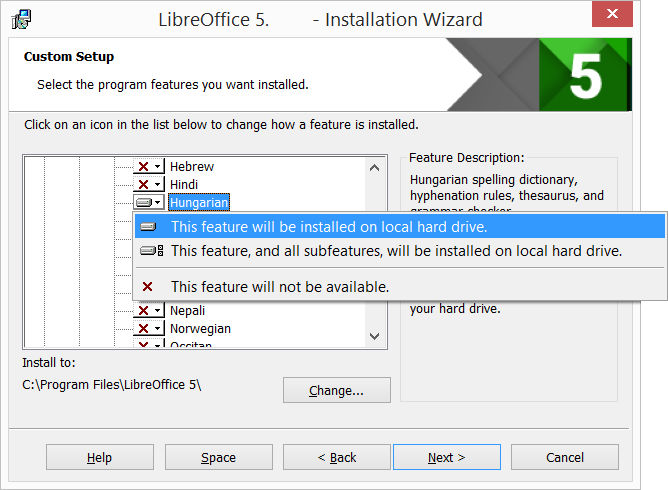
Соответствует состоянию «Custom Changed»
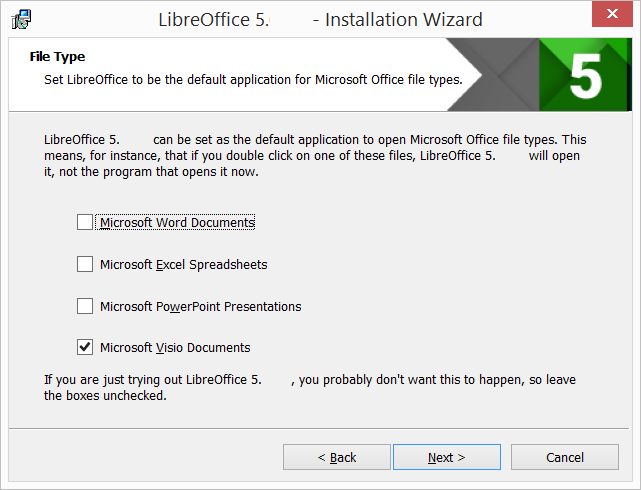
Соответствует состояниям «File Type» и «File Type Changed»
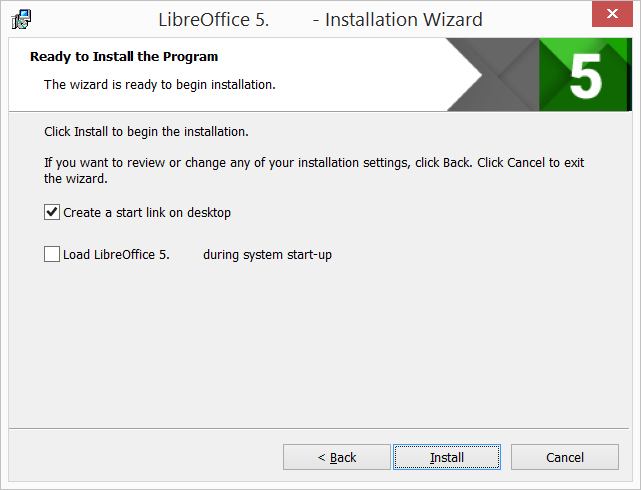
Соответствует состояниям «Ready to Install» и «Ready to Install Changed»
Соответствует состоянию «Installation Progress»
Соответствует состоянию «Installation Complete»
В результате у меня получился граф ниже (использовались английские названия кнопок и короткие названия экранов инсталлятора, чтобы было легче сопоставить со скриншотами). Здесь есть такие метки над стрелками:
- Cancel — Отмена
- Next — Далее
- Back — Назад
- Change — Внесение изменения по сравнению с исходным экраном
Typical и Custom — выбор варианта на втором экране. Часть названия состояний Changed показывает, что в экран были внесены изменения. В состояния, помеченные Changed, можно попасть только из такого же состояния без этой метки в результате перехода «Change».
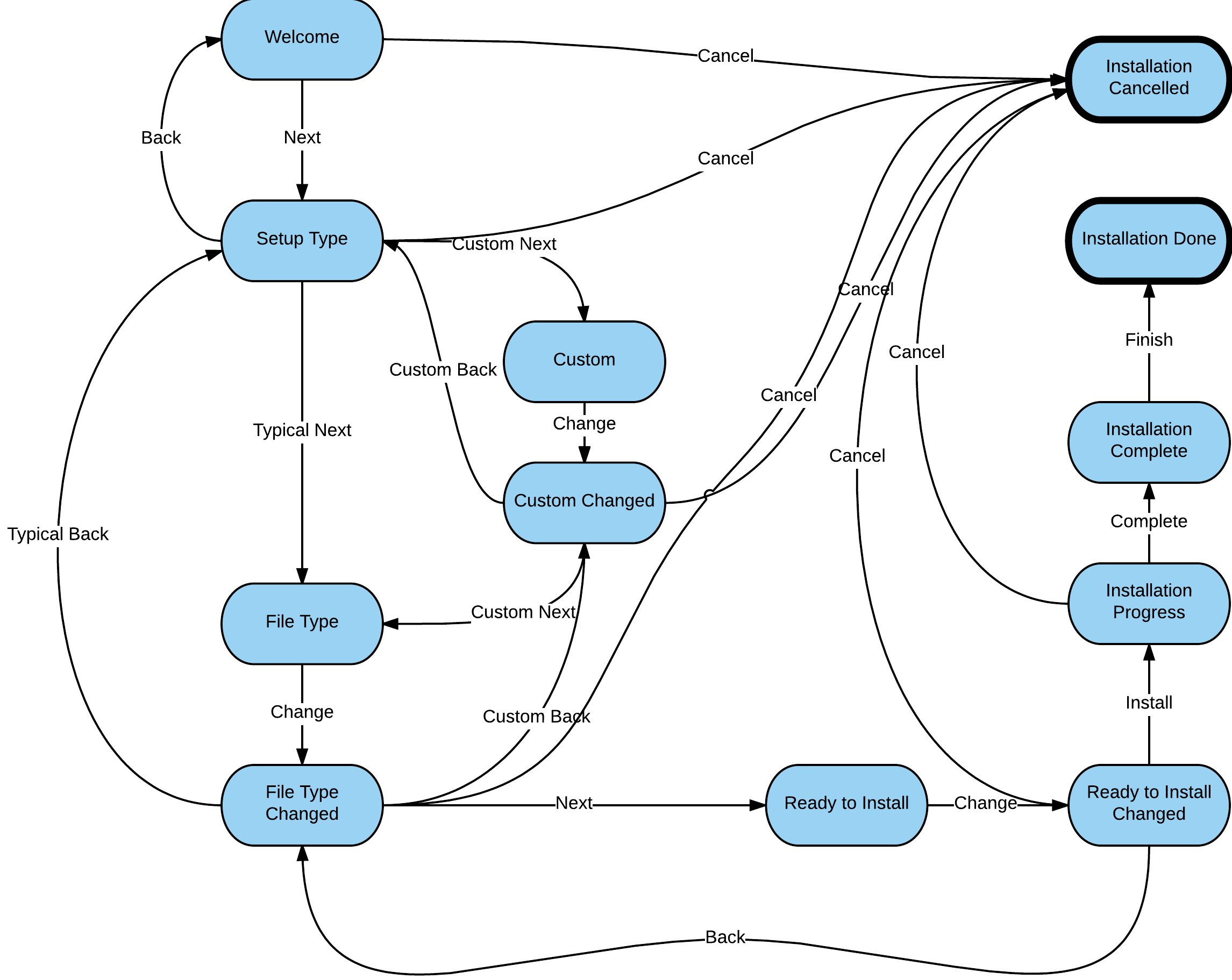
Граф состояний и переходов для инсталлятора
Получилось довольно громоздко, но, надеюсь, поддается расшифровке.
Виды покрытия и наборы тестов
Теперь займемся разными видами покрытия графа и составим соответствующие им достаточные наборы тестов. Для этого перенумеруем состояния, чтобы было легче на них ссылаться (так, как это делалось в первой и второй статьях о покрытии графов). Синтаксис для задания требований и тестов в каждом виде покрытия взят оттуда же.
1 — Welcome
2 — Setup Type
3 — Custom
4 — Custom Changed
5 — File Type
6 — File Type Changed
7 — Ready to Install
8 — Ready to Install Changed
9 — Installation Progress
10 — Installation Complete
11 — Installation Done (конечное состояние)
12 — Installation Cancelled (конечное состояние)
Покрытие вершин
требования = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
путь(T) = {[1, 12], [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]}
Это покрытие достаточно легко реализовать. Его можно посчитать достаточным, но в этих тестах не учитываются ребра, возвращающие в более ранние состояния, из-за которых образовываются циклы. Можно рассчитать цикломатическую сложность этого графа:
ЦС = #ребер – #вершин + 2 = 22 — 12 + 2 = 12
Покрытие ребер и заданных путей
требования = {(1, 12), (1, 2), (2, 1), (2, 12), (2, 3), (2, 5), (3, 4), (4, 12), (4, 2), (4, 5), (5, 6), (6, 2), (6, 4), (6, 12), (6, 7), (7, 8), (8, 6), (8, 12), (8, 9), (9, 12), (9, 10), (10, 11)}
путь(T) = {[1, 12], [1, 2, 12], [1, 2, 3, 4, 12], [1, 2, 5, 6, 12], [1, 2, 5, 6, 7, 8, 12], [1, 2, 5, 6, 7, 8, 9, 12], [1, 2, 1, 2, 5, 6, 2, 3, 4, 2, 3, 4, 5, 6, 4, 5, 6, 7, 8, 6, 7, 8, 9, 10, 11]}
Последний, самый длинный, путь учитывает все изменения и все обратные переходы. Следовательно, этот путь обеспечивает простое покрытие замкнутых путей (один путь для каждого цикла).
Стоит ли обеспечивать другие виды покрытия, зависит от количества шагов инсталлятора, времени, которое потребуется для проектирования необходимых сценариев вручную или автоматизации их составления для заданного покрытия, требуемого уровня качества. На мой взгляд, для этого инсталлятора (и других, впрочем) достаточно как перечисленных выше тестов, так и выбранного вида покрытия.
Автор: Инфопульс Украина