Продолжаем публикацию лекций по предмету "Управление в Технических устройствах" Автор Олег Степанович Козлов. Кафедра "Ядерные энергетические установки" МГТУ им. Н.Э. Баумана. Это вторая лекция, гда теория автоматеского управления применяется непосредственно к таким устройствам как ядерные реакторы.
В предыдущих сериях:
1. Введение в теорию автоматического управления.
2. Математическое описание систем автоматического управления 2.1 — 2.3, 2.3 — 2.8, 2.9 — 2.13.
3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ РЕГУЛИРОВАНИЯ. 3.1 Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ. 3.2 Типовые звенья систем автоматического управления регулирования. Классификация типовых звеньев. Простейшие типовые звенья. 3.3 Апериодическое звено 1–го порядка инерционное звено. На примере входной камеры ядерного реактора. 3.4 Апериодическое звено 2-го порядка. 3.5 Колебательное звено. 3.6 Инерционно-дифференцирующее звено. 3.7 Форсирующее звено. 3.8 Инерционно-интегрирующее звено (интегрирующее звено с замедлением). 3.9 Изодромное звено (изодром). 3.10 Минимально-фазовые и не минимально-фазовые звенья. 3.11 Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности.
4. Структурные преобразования систем автоматического регулирования.
5. Передаточные функции и уравнения динамики замкнутых систем автоматического регулирования (САР).
6. Устойчивость систем автоматического регулирования. 6.1 Понятие об устойчивости САР. Теорема Ляпунова. 6.2 Необходимые условия устойчивости линейных и линеаризованных САР. 6.3 Алгебраический критерий устойчивости Гурвица. 6.4 Частотный критерий устойчивости Михайлова. 6.5 Критерий Найквиста.
7. Точность систем автоматического управления. Часть 1 и Часть 2
8. Качество переходного процесса. Часть 1 и Часть 2
9. Синтез и коррекция систем автоматического регулирования (САР).
10. Особые линейные системы. Часть 1
10.5. Некоторые замечания по численному решению уравнений динамики CAP с запаздыванием. Идентификация запаздывающих звеньев набором простых линейных звеньев.
Расчет CAP, имеющих запаздывающие звенья имеет очень важную особенность, а именно: требуется хранить в оперативной памяти практически все промежуточные результаты расчета, что приводит (или может привести) к неприятным последствиям (увеличение расхода памяти), по сравнению с обычными диференциальными уравнениями.
Эти проблемы возникают, например, при решении задач в форме Коши (система обыкновенных дифференциальных уравнений):
Обычная САР:
САР с запаздыванием:

В случае обычной CAP правые части уравнений – обычные линейные функции переменных состояния, и поэтому проблем решения не существует например, с использованием матричных способов, или, например, с использованием конечно-разностных методов (Рунге-Кутта, Адамса и т.д.).
В случае CAP с запаздыванием необходимо сохранить все предыдущие результаты расчета по тем переменным состояния, которые используются и с запаздывающим аргументом. Например, если системе Коши , а
, то необходимо на каждом шаге расчета (при t = t) использовать информацию о поведении
при
;
Одним из наиболее эффективных способов решения («обхода») возникших трудностей является использование методов идентификации, заключающихся в замене запаздывающих элементов на более простые звенья (или набор звеньев) без особой потери точности.
Наибольшее распространение получили 2 способа:
- замена запаздывающего звена обыкновенным (типовым) звеном 2-го порядка;
- идентификация запаздывающего звена цепью из последовательно соединенных генерирующих звеньев (а период 1-го порядка).
Рассмотрим обоснование таких замен и их ограничения:
Замена звеном 2-го порядка:
раскладывая в ряд Тейлора:
Отбрасывая слагаемые большего порядка малости
А это подозрительно похоже на колебательное звено
Такой «прием» правомочен (корректен), если на CAP воздействуют только низкочастотные управляющие сигналы и τ – не велико.
это предельный случай т.е.
не имеет «горба».
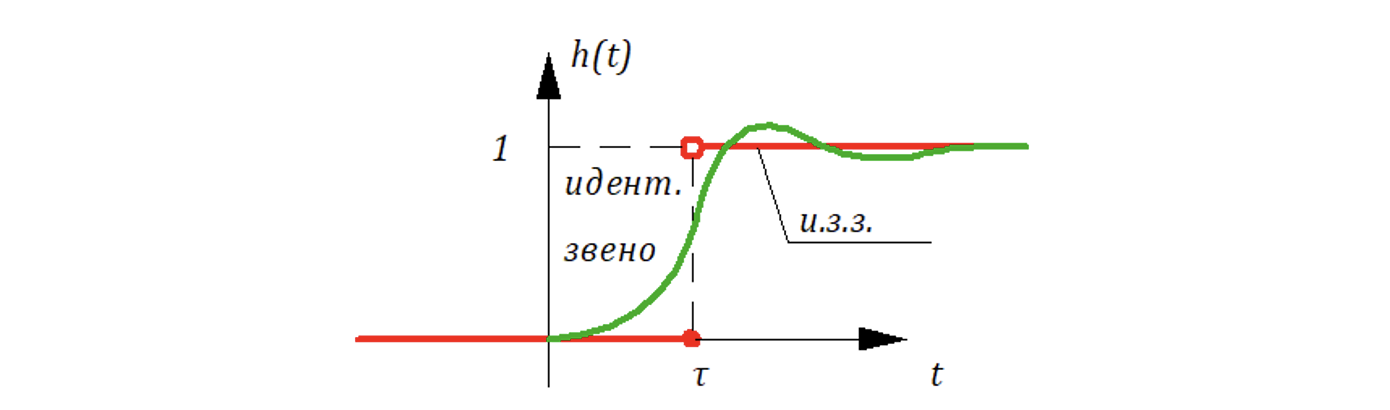
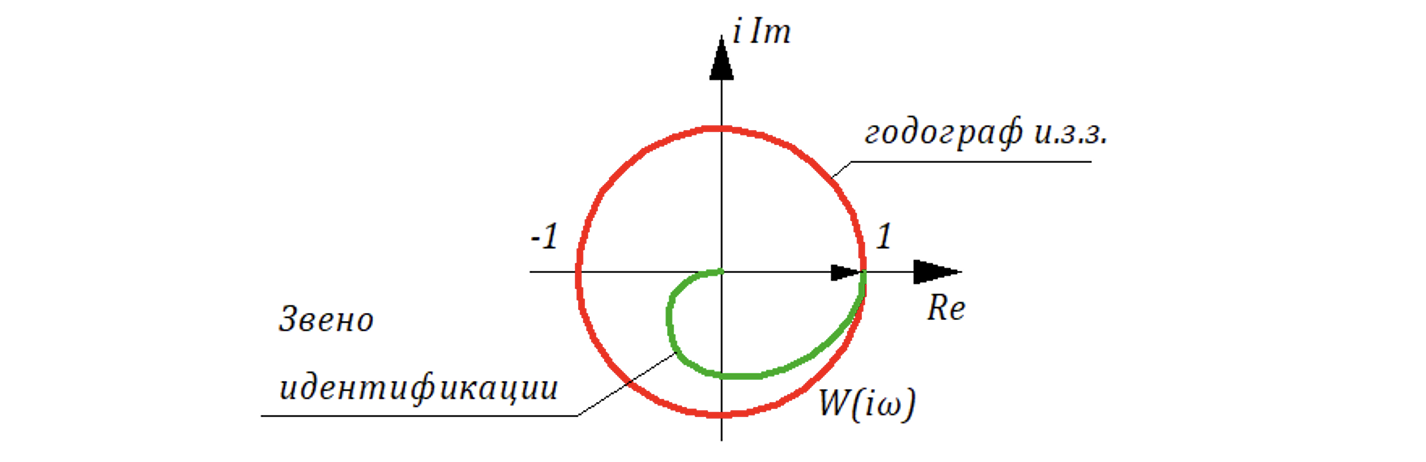
Замена (идентификация) цепью из последовательно соединенных инерционных звеньев.
Идея этого способа основана на следующих замечательных пределах:

Т.к. имеется цепь из последовательно соединенных звеньев, то
если n достаточно велико, то
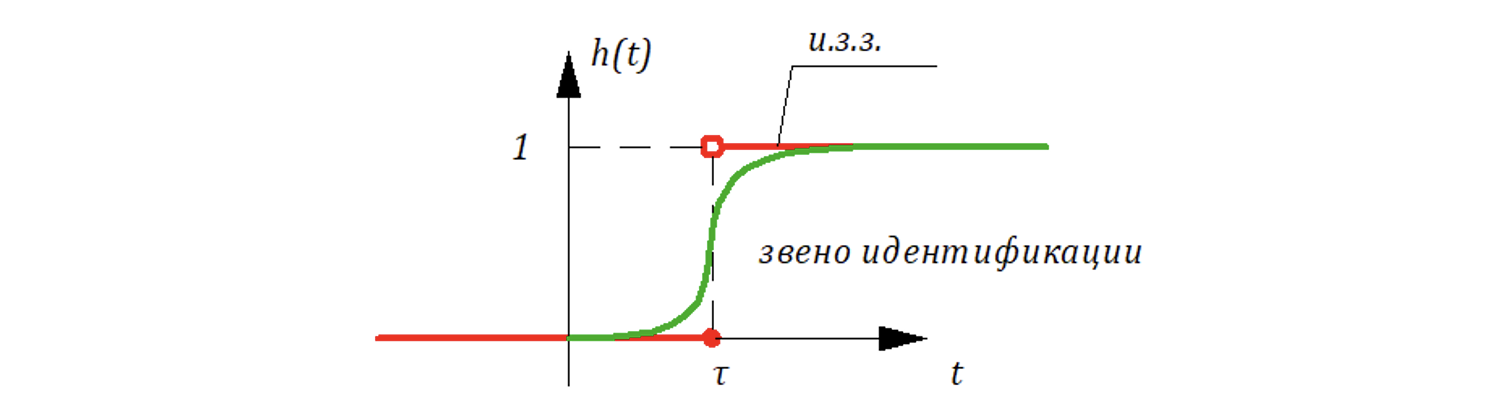
Практика (опыт) показывает, что если n = 6 - 8(10), то свойство запаздывания идентифицируется почти точно (с очень небольшой погрешностью), см. рис. 10.5.4.
10.6 Простейшие трансцендентные звенья
На стадии приближенной оценки динамических характеристик теплогидравлического оборудования АЭС (парогенератор, теплообменник, сепаратор), тепловой автоматики (датчики теплового потока, термопары и т.д.), тепловыделяющих сборок, используется точечное описание нестационарных теплообменных процессов, когда элементы реакторной установки (имеющие, кстати, немалые размеры) в динамическом (нестационарном) плане представлялись материальной точкой, описываемой простейшим нестационарным уравнением теплового баланса типа:
где:
- источниковый член, описывающий теплоту (энергию), выделившуюся в объеме рассматриваемого элемента (или переданную);
- «стоковый» член, описывающий отвод теплоты от рассматриваемого элемента (тела);
- температура элемента (тела).
Однако, при уточнении математического описания нестационарных процессов уравнение динамики переходит в класс уравнений с частными производными, поскольку для описания процессов переноса тепла приходится использовать нестационарное уравнение теплопроводности:
где:
- радиус-вектор;
- конвективный перенос тепла;
- коэффициент теплопроводности;
- источник и сток, соответственно.
Если температура некоторого элемента (звена) в любой момент времени является также функцией (явной или неявной) только одной пространственной координаты (например, длины или радиуса), то такое звено считается линейно-распределенным, а вся САР – линейно-распределенной.
Уравнение теплового баланса принимает, например, следующий вид (без внутреннего источника тепла):
где:
u - скорость тепоноситлея;
B - коэффициент, характеризующий теплоотдачу.
Примером линейно-распределенного звена может служить полубесконечное тело, нагреваемое, например, лучистым потоком (излучением), падающим перпендикулярно поверхности.
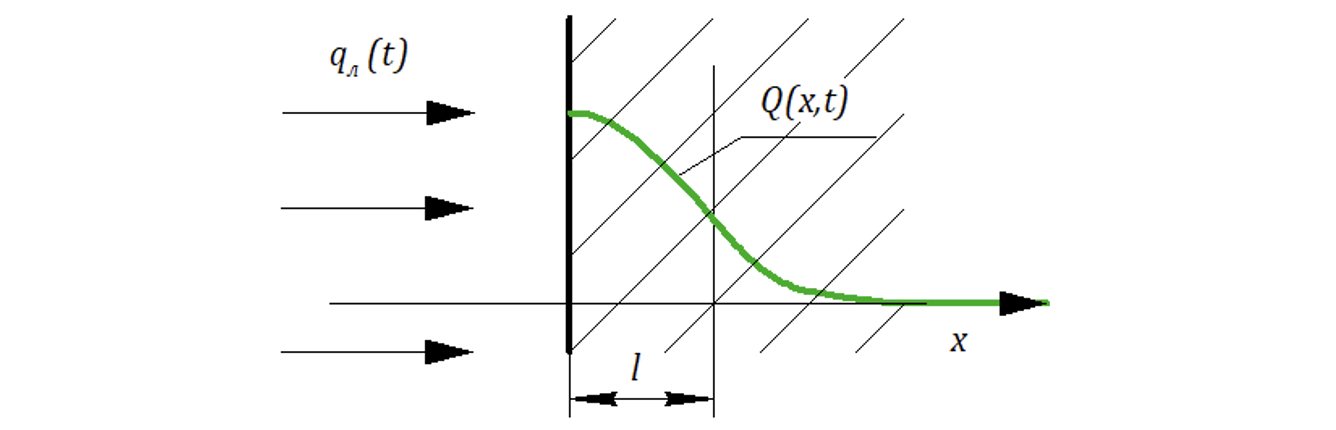
Уравнение теплового баланса в этом случае принимает вид:
В отличие от описания сосредоточенных моделей (точечное приближение) в данном случае задача формулируется несколько шире:
Точечное приближение:
-
уравнение или система уравнений;
-
начальные условия.
Линейно-распределенная САР (нестационарная краевая задача):
-
уравнение или система уравнений;
-
начальные условия;
-
граничные условия (Г.У.).
Поэтому вывод передаточных функций (если это возможно) и сам процесс решения задачи в линейно-распределенных САР заметно (если не намного) сложнее.
Поскольку мы рассматриваем нестационарные тепловые процессы только в полубесконечном теле, то условия, связанные с лучистым потоком () и охлаждением полутела (
) входят либо в начальные (Н.У.) или граничные условия (Г.У.).
В стационарном состоянии уравнение принимает вид:
В общем случае можно представить как сумму стационарной и нестационарной составляющих:
перейдем к безразмерной переменной
если лучистый поток , то
- температура окружающей среды.
Подставляя в уравнение (10.6.4) и введя новую перменную
температуропроводность, имеем:
Поскольку, в соответствии с условием (10.6.5)
следовательно, уравнение принимает вид:
Выполним решение уравнения (10.6.7) операторным методом, используя двумерные преобразования Лапласа:
Tгода уравнение теплороводности в изображениях принимает вид:
где: - новая постоянная.
Характеристическое уравнение, соответствующее однородному дифференциальному уравнению (10.6.8) имеет «традиционный» вид:
где постоянные и
находятся из граничных условий. Учитывая, что при
мы должны получить не бесконечно большое значение T,
условие ограниченности требует
. Тогда:
Значение постоянной , в принципе, может быть найдено из второго граничного условия, а именно, при
, хотя в данном случае мы этого и не будем делать.
Изображения при
и
принимают следующий вид:
Рассмотрим теперь различные типы граничных условий, которые определяют тепловое состояние при .
10.6.1 Полузапаздывающее звено (граниченое условие 1-го рода)
Предположим, что процесс теплообмена в полубесконечном теле можно описать какой-то передаточной функцией, где входным воздействием будем считать температуру поверхности , а выходным результатом температуру на расстоянии l tilde(T)(l,t), см. рисунок:
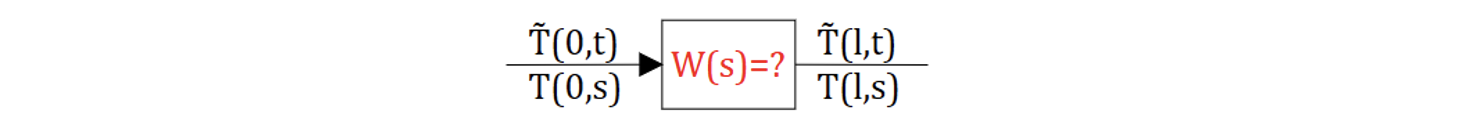
По определению:
где: - время задержки.
Выражение (10.6.12) соответствует передаточной функции полузапаздывающего звена (т.к. есть )
Рассмотрим динамические свойства этого звена
АФЧХ
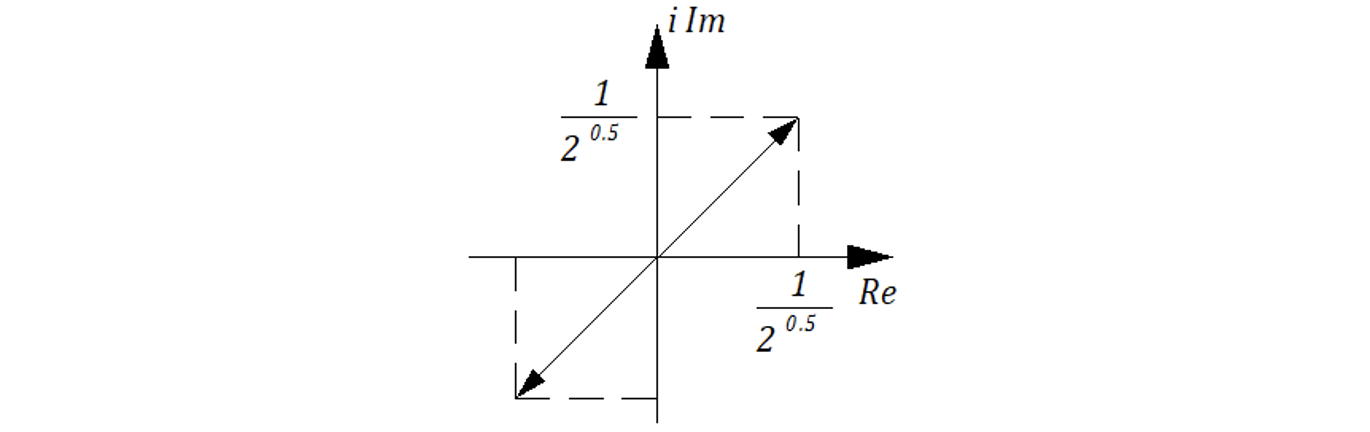
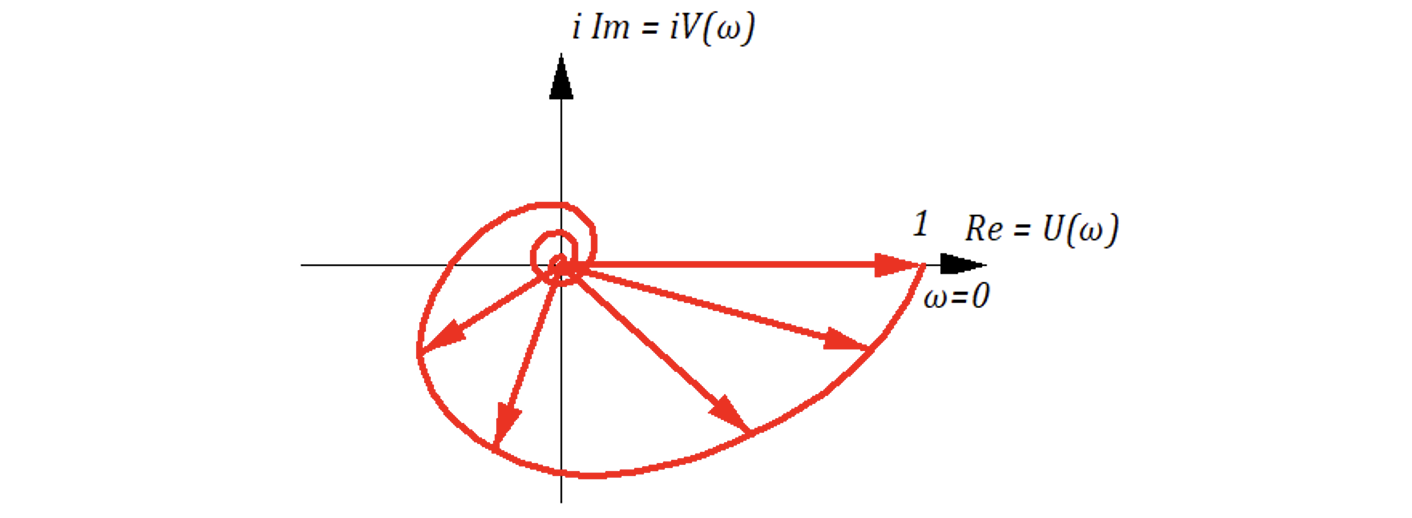
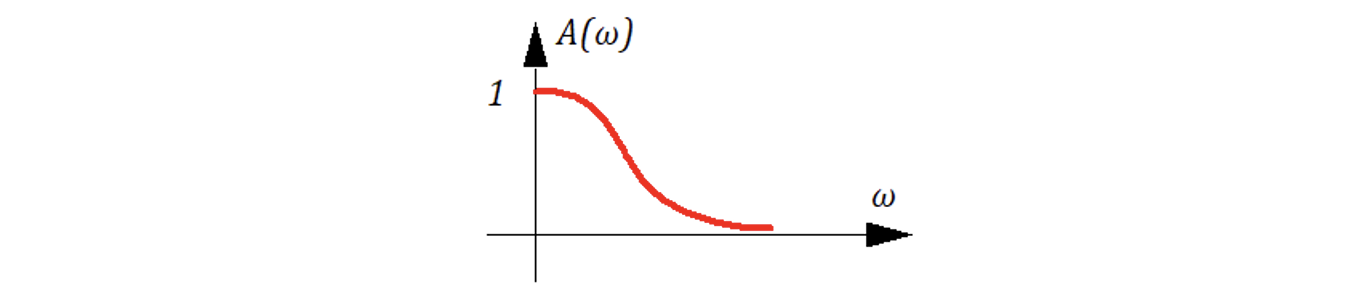
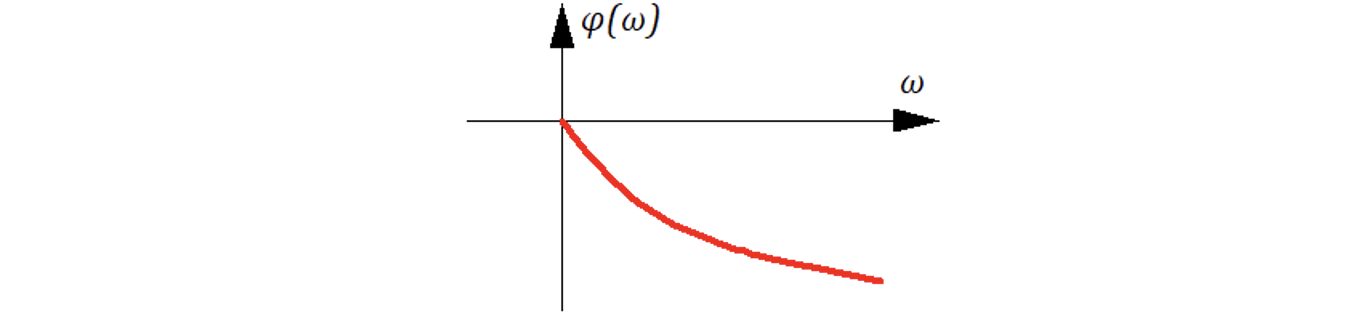
ЛAX:
Переходная функция:
Предположим, что в момент времени безразмерная температура левой стенки «полутела» изменилась скачком и поддерживается постоянной и равной 1, следовательно,
, следовательно, реакция звена в этом случае соответствует переходной функции:
Вот так рассматривая температуру стенки мы вышли на замечательную функцию ошибок Гаусса:
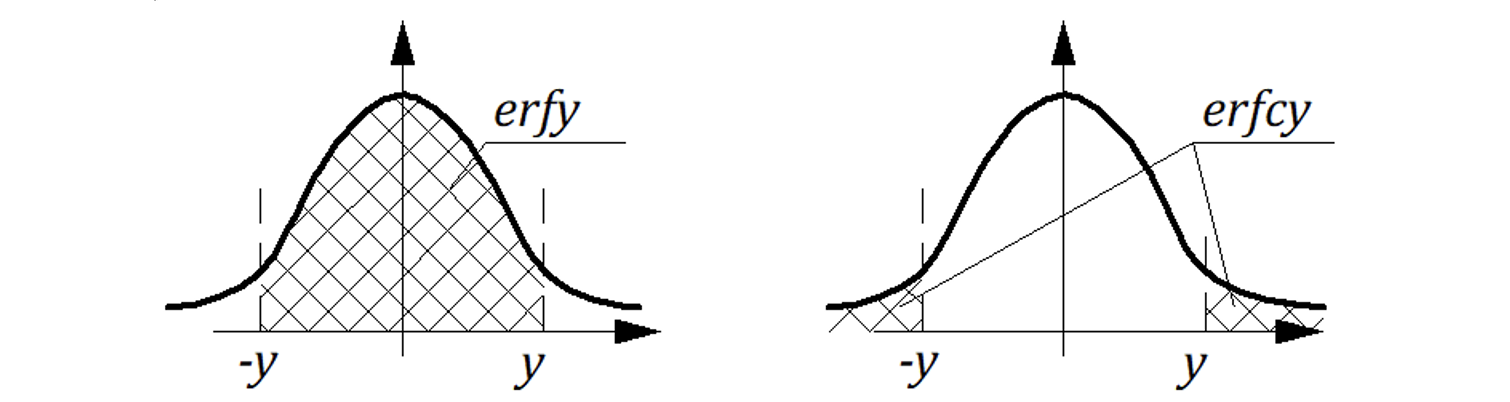
Весовая функция:
Введем новую переменную относительное время тогда весовая функция:
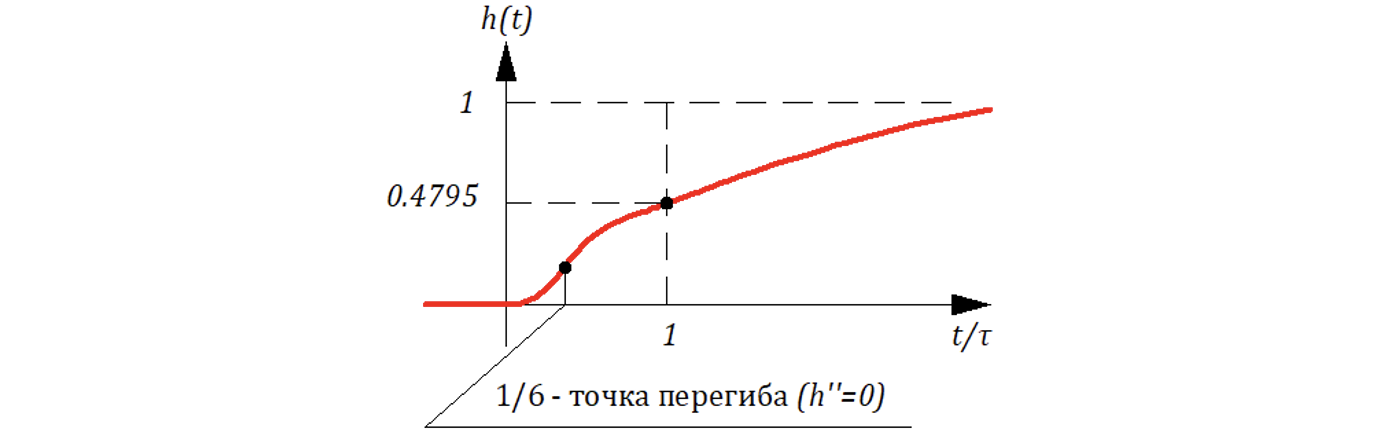
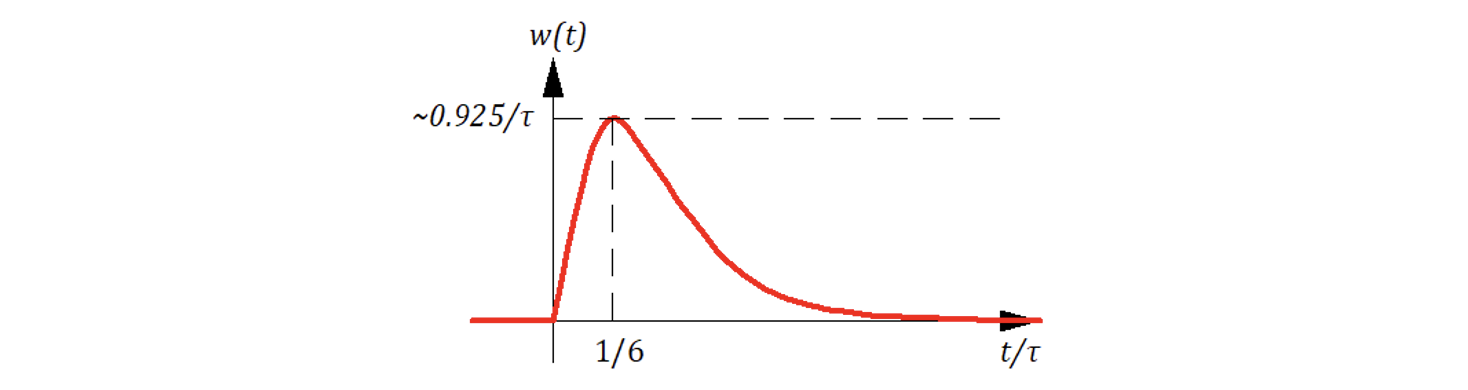
По внешнему виду переходная h(t) и весовая w(t) функции звена «похожи» на соответствующие функции апериодического звена 2-го порядка.
Примером полузапаздывающего звена может служить термопара (малоинерционная) «зачеканенная» в массивную стенку (например, в бетонный корпус биологической защиты).
10.6.1 Полуинтегрирующее звено (граниченое условие 2-го рода)
Рассмотрим другое граничное условие при . На стенке задан тепловой (лучистый) поток
. Тогда входным воздействием будем считать тепловой поток на стенку, а выходным воздействием – температуру поверхности «полутела»:

Данную задачу можно трактовать следующим образом: при лучистый поток скачком изменился. Что будет с температурой поверхности?
Учитывая, что , подставим в формулу (10.6.17):
где:
Выражение (10.6.20) соответствует передаточной функции полуинтегрирующего звена (т.к. есть.
Определим динамические свойства этого звена:
АФЧХ (не могу удрежатся что бы не вывести):
Из формул 10.6.22 получаем выражение амплитуды для
:
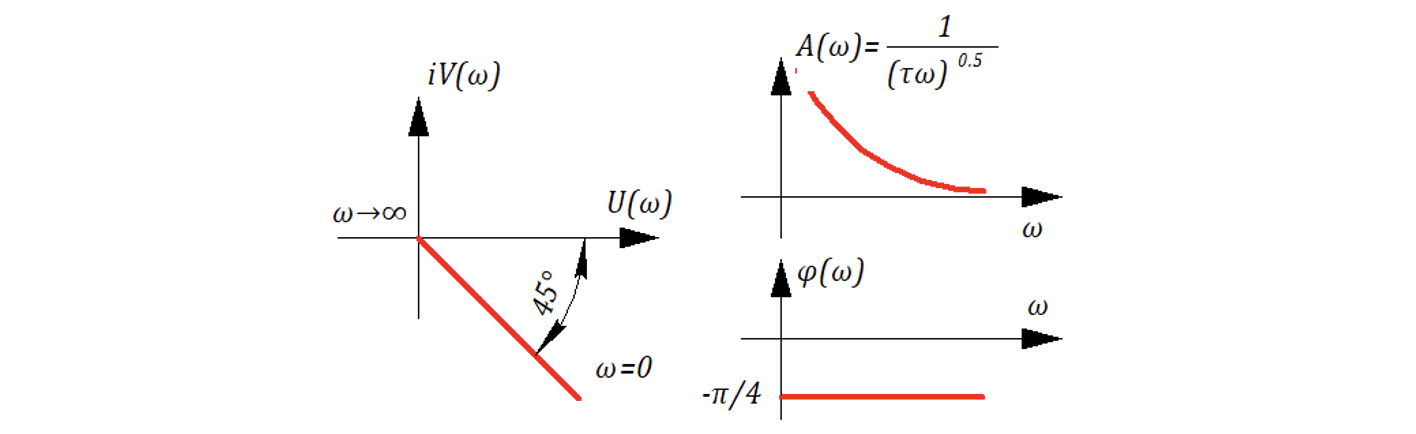
 ,
, ,
,  .
.ЛАХ Логарифмическая амплитудная характеристика:
Из формулы (10.6.24) следует, что наклон равен -10дБ/дек:
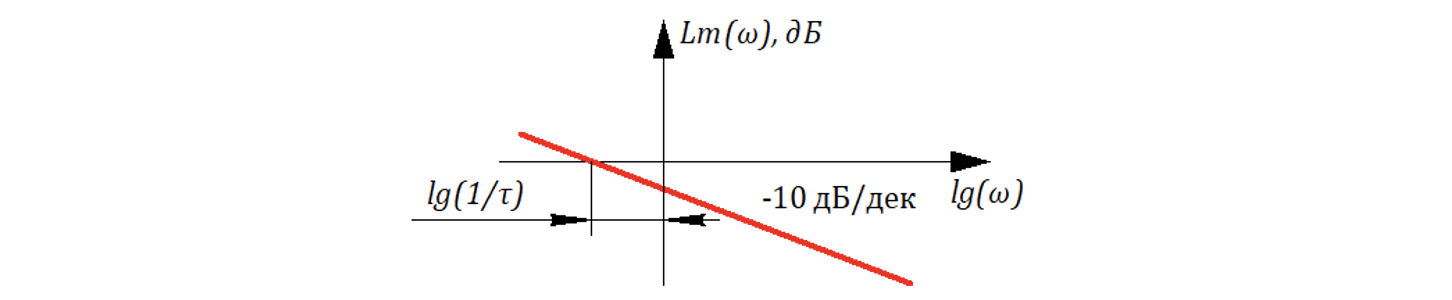
Поскольку данное звено полуинтегрирующее, то и наклон ЛАХ равен половине от обычного интегрирующего, т.е. наклон = ½ (-20дБ/дек) = -10дБ/дек
Найдем переходную и весовую функции звена:
Переходная функция :
Весовая функция звена :
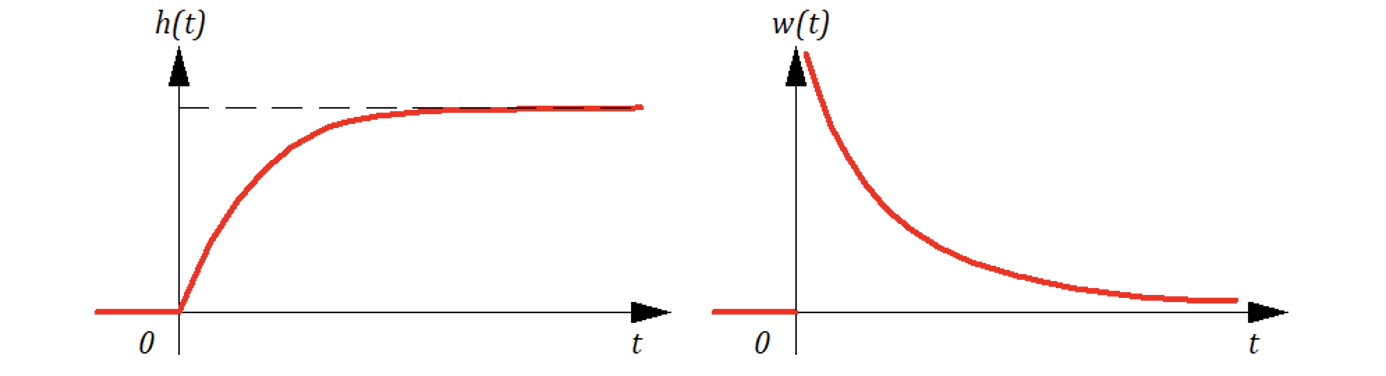
10.6.3 Полуинерционное звено (Г.У. 3-го рода)
Рассмотрим еще одно Г.У. при - на поверхности задан тепловой поток и закон теплосъема, т.е. поверхность охлаждается какой-то (прозрачной) жидкостью.
Следовательно, лучистый поток, падающий на стенку, отводится вглубь тела теплопроводностью и в охлаждающую жидкость посредством конвективного обмена. Тогда уравнение физики, c учетом коэффициент теплоотдачи будет выглядеть так:
Пусть входным воздействием будет , а выходным воздействием
– температура поверхности, тогда:
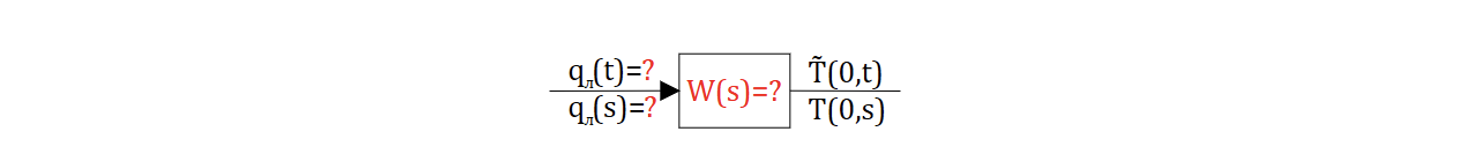
Передаточная функция:
Подставляя в выражение (10.6.28) значение и
, получаем:
где:
Выражение (10.6.29) соответствует передаточной функции полуинерционного звена (полуапериодическое 1-го порядка).
Определим динамические свойства данного звена:
Следовательно, опуская выкладки, нарисуем графики:
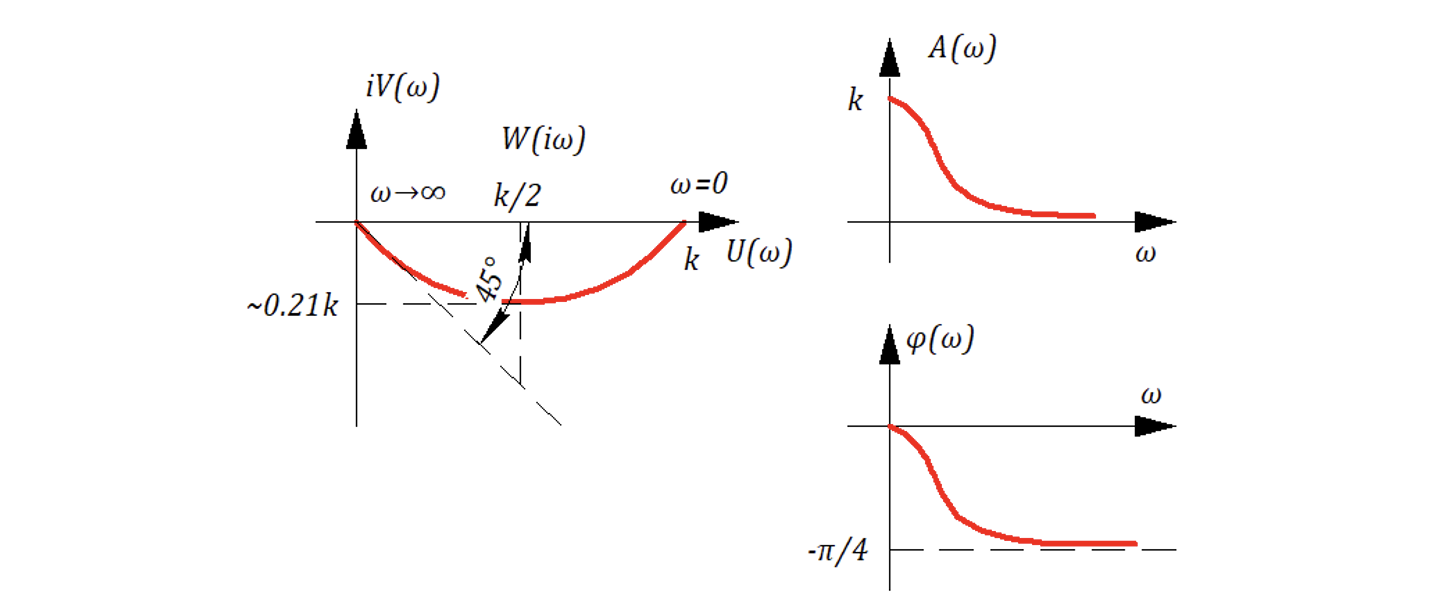
Амплитуда:
ЛАХ:
Анализ формулы (10.6.30) показывает, что при асимптотический наклон ЛАХ будет составлять -10 дБ/дек.
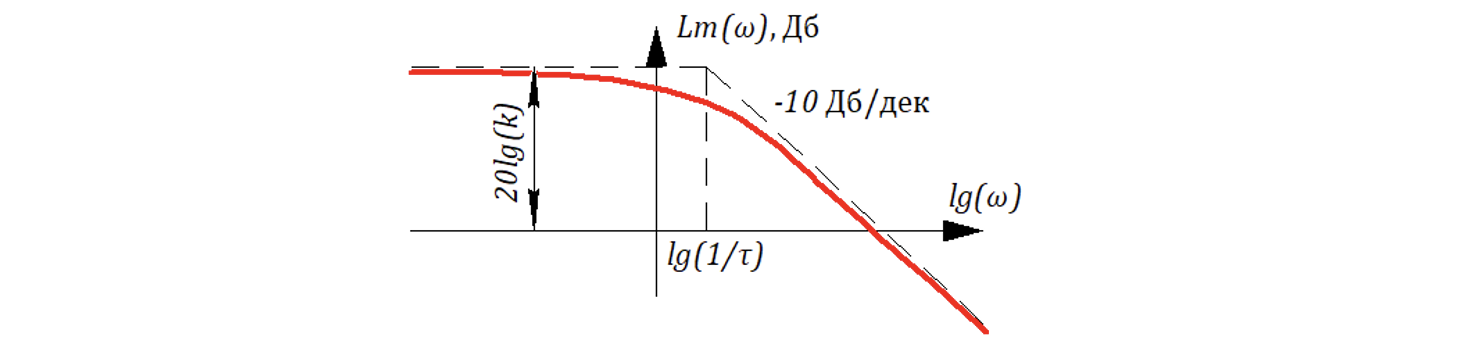
Внешне ЛАХ «похож» на ЛАХ апериодического звена 1-го порядка, только наклон равен -10 дБ/дек.
Найдем выражения для переходной и весовой функции
:
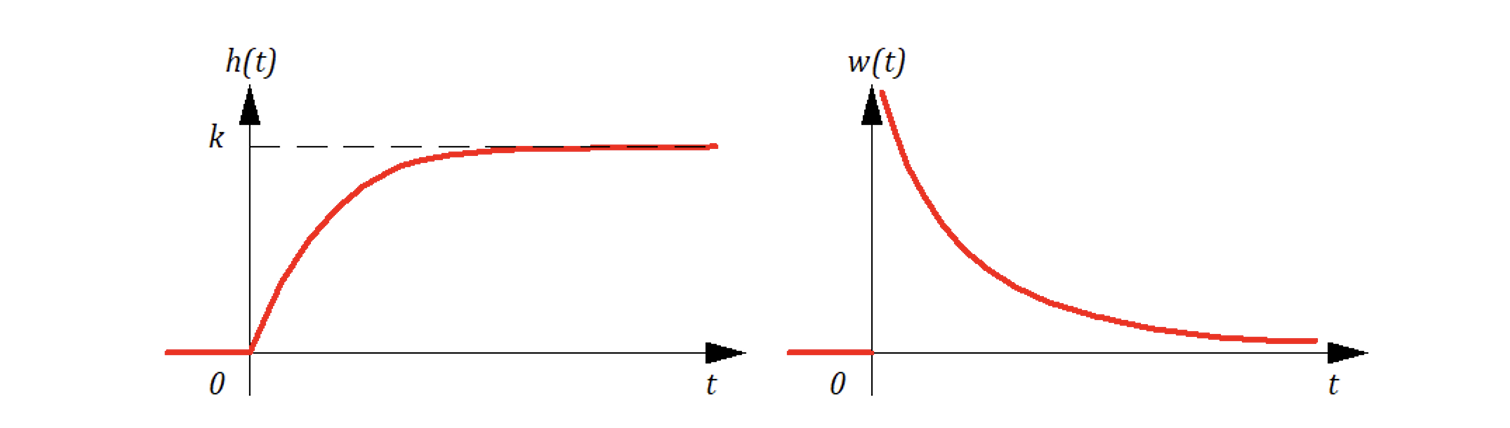
Автор: petuhoff



![10. Особые линейные системы. Часть 2 - 25 rhocdot ccdotfrac{partial theta(vec{r}cdot t)}{partial t}=frac{1}{vec{r}}cdotfrac{partial}{partialvec{r}}left[lambdacdotvec{r}cdotfrac{partialtheta(vec{r},t)}{partialvec{r}}right]+Q_1(vec{r},t)-Q_2(vec{r},t)+Q_k(vec{r}cdot t) \mathbf{(10.6.1)}](https://www.pvsm.ru/images/2025/02/20/10-osobye-lineinye-sistemy-chast-2-25.svg)
![10. Особые линейные системы. Часть 2 - 38 tilde{T}(x,t)=frac{theta(x,t)-theta(x,0)}{theta(x,0)}Rightarrow theta(x,t)=theta(x,t)cdot[1+tilde{T}(x,t)] mathbf{(10.6.6)}](https://www.pvsm.ru/images/2025/02/20/10-osobye-lineinye-sistemy-chast-2-38.svg)




![10. Особые линейные системы. Часть 2 - 80 begin{align} Lm(omega)=20cdot lg[A(omega)]=20cdotleft[ -frac{sqrt{2cdot taucdot omega}}{2}cdot lg(e)right]=\=-10cdot lg(e)cdotsqrt{2cdot taucdotomega}=-(10cdot lg(e)cdotsqrt{2cdot tau})cdotsqrt{omega}end{align}](https://www.pvsm.ru/images/2025/02/20/10-osobye-lineinye-sistemy-chast-2-80.svg)
![10. Особые линейные системы. Часть 2 - 84 h(t)=Z^{-1}[H(s)]=Z^{-1}left[frac{W(s)}{s}right]=Z^{-1}left[frac{e^{-sqrt{taucdot s}}}{s}right]=erfcleft[frac{1}{2}sqrt{frac{tau}{t}}right]](https://www.pvsm.ru/images/2025/02/20/10-osobye-lineinye-sistemy-chast-2-84.svg)









![10. Особые линейные системы. Часть 2 - 118 h(t)=Z^{-1}[H(s)]=Z^{-1}left[frac{W(s)}{s} right]=Z^{-1}left[frac{1}{scdotsqrt{taucdot s}} right]](https://www.pvsm.ru/images/2025/02/20/10-osobye-lineinye-sistemy-chast-2-118.svg)









