С этой структурой данных можно ознакомиться в этом посте и её модификацией для нахождения максимума в этом. Но я нигде не встречал реализацию с изменением элементов на отрезке, поэтому решил поделиться тем, что сумел получить самостоятельно.
1. Постановка задачи
Имеется массив. Необходимо уметь выполнять запросы двух видов:
- Модификация — прибавить d к каждому элементу отрезка [l, r]
- Сумма — вычислить сумму элементов отрезка [l, r]
2. Описание решения
Нетрудно заметить, что оба вида запросов можно «облегчить» до отрезка [0, r], разбивая отрезок [l, r] на два префикса. Как и для дерева отрезков, заведём второй массив, в котором будем хранить сколько надо прибавить ко всем числам этого отрезка.
Создадим класс Fenwick с прототипами будущих методов.
class Fenwick{
int *m, *mt, N;
public:
Fenwick(int n);
Fenwick(int a[], int n);
void add_range(int r, int d);
void add_range(int l, int r, int d);
int sum(int r);
int sum(int l, int r);
};
В первом конструкторе достаточно выделить память и обнулить элементы массива. А во втором ещё пройдёмся по массиву a и прорелаксируем значения в дереве.
Fenwick::Fenwick(int n){
N = n;
m = new int[N];
mt = new int[N];
memset(m, 0, sizeof(int)*N);
memset(mt, 0, sizeof(int)*N);
}
Fenwick::Fenwick(int a[], int n){
N = n;
m = new int[N];
mt = new int[N];
memset(m, 0, sizeof(int)*N);
memset(mt, 0, sizeof(int)*N);
for(int i=0;i<N;++i){
m[i] += a[i];
if((i|(i+1))<N) m[i|(i+1)] += m[i];
}
}
Рассмотрим теперь операцию изменения. Предположим пришёл запрос «прибавить 1 к элементам отрезка [0, 9]». Этот отрезок полностью покрывается непересекающимися отрезками [0, 7] и [8, 9], поэтому в 7 и 9 элементы массива mt прибавляем 1. Но есть отрезки, содержащие [0, 9] (или его часть) в качестве подотрезка. Все они располагаются справа. Для них необходимо изменить значение в массиве m на столько, сколько элементов отрезка [0, 9] они содержат. То есть в m[11] прибавить 2, а к m[15] — 10.
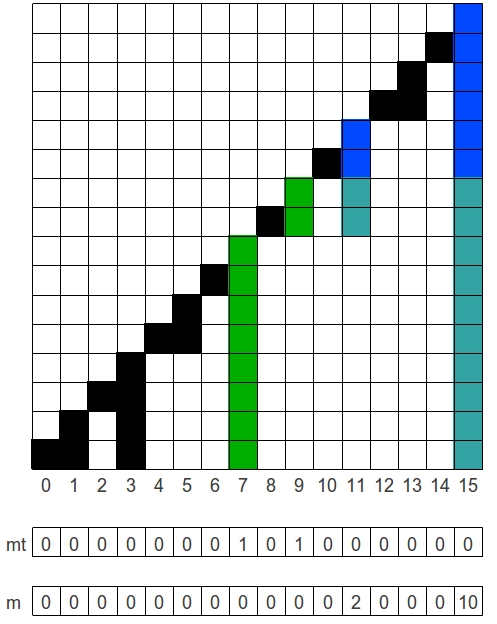
Из рисунка видно, что перемещения происходят по тем же законам, что и в тривиальной реализации дерева Фенвика, поэтому сразу перейдём к коду.
void Fenwick::add_range(int r, int d){
if(r<0) return ;
for(int i=r;i>=0;i=(i&(i+1))-1) mt[i] += d;
for(int i=r|(r+1);i<N;i|=i+1) m[i] += d*(r-(i&(i+1))+1);
}
void Fenwick::add_range(int l, int r, int d){
add_range(r, d);
add_range(l-1, -d);
}
Для суммы на префиксе подойдёт та же картинка с тем лишь пояснением, что для зелёных элементов необходимо прибавить и m, и mt, а для синих только mt (то есть учесть большие накрывающие отрезки).
int Fenwick::sum(int r){
if(r<0) return 0;
int res = 0;
for(int i=r;i>=0;i=(i&(i+1))-1) res += m[i] + mt[i]*(i-(i&(i+1))+1);
for(int i=r|(r+1);i<N;i|=i+1) res += mt[i]*(r-(i&(i+1))+1);
return res;
}
int Fenwick::sum(int l, int r){
return sum(r) - sum(l-1);
}
3. Итоги
Нам удалось получить структуру данных с инициализацией за O(N), модификацией и суммой на отрезке за O(logN). На рандомном тесте с 10000000 элементов и 10000000 запросов получил такие цифры:
| Структура данных | Инициализация | Модификация | Сумма |
|---|---|---|---|
| Fenwick | 0.13 с | 9.12 с | 8.90 с |
| RSQ (реализация с e-maxx) | 0.25 с | 17.13 с | 13.53 с |
Автор: kormyshov
