Нет, это не просто картинка для красоты. Это – Алёна, участница эксперимента. Которая именно танцем внесла в него основной вклад. Впрочем, обо всём по порядку.

Каждый фотограф знает, что чем длиннее экспозиция, тем чаще (при прочих равных параметрах) изображения движущихся людей оказываются смазанными.
Вопрос: а как вероятность этого зависит от экспозиции?
По этому поводу возможны многочисленные теоретические соображения. Но теория без эксперимента – это как тост без вина. А потому был проведён эксперимент:
- Расставлена фотостудия.
- Включена музыка.
- Приглашена Алёна.
- Которая танцевала...
- … пока я в случайные моменты времени делал со штатива фотографии с разными экспозициями, набрав их в итоге несколько сотен...
- … и подсчитав в конце долю чётких среди них.
Читать дальше про методику и результаты.
Разумеется, резкость кадра – вопрос сложный и во многом субъективный. Для однозначности было решено считать чётким фото, на котором хорошо и отчётливо получились глаза. Это, конечно, упрощение, но не бесконечно далёкое от реальности. Ведь известно, что даже сильно «замыленный» кадр с нормально получившимся лицом воспринимается терпимо, а вот обратное — уже нет:

Непосредственные результаты
На графике — измеренная в эксперименте вероятность сделать технически резкий кадр в зависимости от экспозиции:
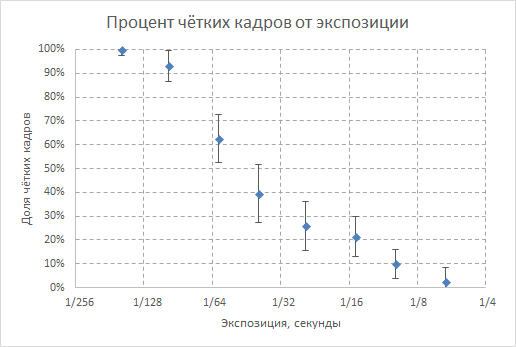
«Усы» характеризуют неопределённость измерений из-за ошибок округления (±0.5 кадра) и ожидаемого биномиального шума в ±1σ.
На качественном уровне всё как и ожидалось. Когда экспозиция растёт чёткие кадры теряются. Однако неплохо бы эту зависимость не только увидеть, но и ещё понять. Охарактеризовать количественно.
Для этого вместо абсолютной вероятности успеха посмотрим на отношение шансов сделать плохой кадр к шансам на хороший:
Y = (количество запоротых кадров)/(количество удачных кадров)
В этих терминах график приобретает простой и изящный вид:
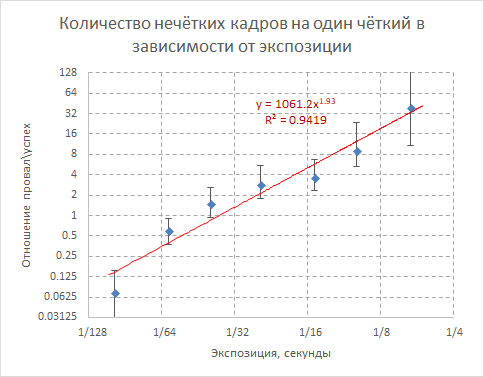
Красная прямая — степенная зависимость, вписанная в экспериментальные данные. Её показатель (1.93) весьма близок к двум. И я сильно подозреваю, что «на самом деле» это именно двойка и есть, с точностью до ошибок измерений.
Почему?
Немного теории
Чтобы это понять, рассмотрим проекцию движения глаз танцора на горизонтальную ось x матрицы фотоаппарата. Пусть оно описывается функцией x(t). Строгим условием чёткости изображения будет его невыход за некоторый предел r в течение всей съёмки длительностью dt:
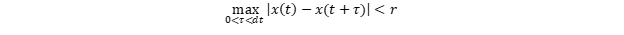
Поскольку для получения «достаточно приличного» кадра этому условию не обязательно выполняться абсолютно точно (нас устраивает ошибка до десятков процентов), внесём упрощение. Будем считать, что за время съёмки dt перемещение x(t) хотя бы приблизительно линейно, т.е.:
x(t + τ) ≈ x(t) + τ*vx(t)
Тогда условие чёткости перепишется как:
|vx(t)| < r/dt
Здесь vx(t) — скорость движения вдоль оси x в момент открытия затвора t.
Далее, что мы знаем про скорость глаз? Что это сложный набор наложенных друг на друга движений сразу нескольких суставов: стопы, колена, бедра, корпуса, шеи. Таким образом, vx(t) можно представить как суперпозицию нескольких более простых скоростных компонент:
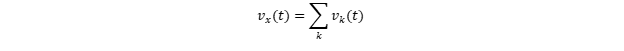
Каждую из этих компонент в заданный момент времени t можно считать случайной [для зануд: танец — квазипериодическое движение; разложим его в ряд Фурье и вспомним, что фаза каждой компоненты для фотографа действительно случайна]. На первый взгляд, это мало чем нам помогает. Ведь мы не знаем ни свойств, ни даже вида распределений этих случайных величин. Казалось бы, кольцевой тупик? Но тут на помощь приходит Центральная Предельная Теорема, гласящая, что при суммировании большого количества слабозависимых случайных переменных, сопоставимых по величине, результат будет стремиться к нормальному распределению — даже если входные распределения далеки от такового! И на практике это часто работает уже при сложении 3-4-х величин.
Что даёт нам основание полагать величину vx(t) нормально распределённой:
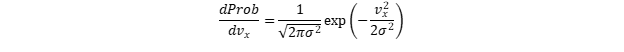
Причём, да, со средним μ = 0. Почему? Потому что движение танцора ограничено сценой, а, значит, суммарное перемещение за большое время (т.е. средняя скорость) равны нулю. Впрочем, на практике фотограф обычно «ведёт» свою цель объективом, что обеспечивает даже более строгое ограничение на среднее движение.
Дальнейшее тривиально. С какой вероятностью |vx(t)| < r/dt? Классический ответ по учебнику:
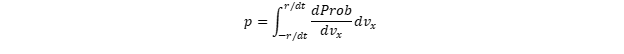
Когда экспозиции велики, интеграл набирается только по узенькой центральной полосочке, внутри которой функция — примерно константа, и ответ превращается в:
p = 2r/(dt*σ√(2*π))
Т.е., вероятность случайно угадать правильный момент открытия затвора убывает как 1/dt.
Теперь вспомним, что матрица фотоаппарата всё-таки двумерна, и, чтобы кадр был чётким, надо угадать момент не только для оси x, но для y. (Упрощаем, упрощаем, незачем вычислять √(x2 + y2)). Если эти моменты, как можно ожидать, статистически малозависимы, то вероятности угадать перемножаются, и получается:
p = const/dt2
— что асимптотически совпадает с наблюдениями в эксперименте.
Итог
С учётом этого результата я, таким образом, готов записать следующую формулу для вероятности сделать несмазанный кадр танцора как функцию экспозиции dt:
p = 1/(1 + (dt/dt0)2) (10)
Здесь dt0 – та экспозиция, при которой в брак уходит 50% отснятого.
Этот вывод легко обобщается не только на танец, но и на многие сложные квазипериодические движения, где есть простой критерий чёткости кадра, а само движение можно считать двумерным (т.е., например, не требующим радикальной перефокусировки в каждый момент). Снимаете ли вы вратаря-хоккеиста, колибри у цветка, или дружескую пьянку за столом — вероятность успеха на «длинном» конце экспозиций убывает как 1/dt2.
Смаз от дрожания рук, кстати, скорее всего, описывается этой же зависимостью, что может объяснять истории про удачные кадры на 1/5 секунды при 35 мм с рук.
Чем полезен этот результат?
Тем, что показывает: не так уж страшно снимать при плохом свете. Да, с падением освещённости вероятность успеха падает — но полиномиально, а не экспоненциально. А с такой зависимостью вполне можно и пободаться.
Во-вторых, он позволяет прикидывать необходимые объёмы съёмки.
Пример. Допустим, Вы фотографируете вечеринку. Динамика её такова, что уже при 1/30 секунды половина портретов оказывается смазанной. А свет пригасили и камера, даже на предельном ISO, подняться выше 1/10 секунды не позволяет. Каковы шансы на успех? Подсчитываем ожидаемую долю чётких кадров:
p = 1/(1 + (30/10)2) = 1/(1+9) = 1/10 = 10%
Мало, но отнюдь не безнадёжно. Если отбабахать пару сотен снимков, то после из них скорее всего удастся извлечь около 200*0.1 = 20 технически хороших изображений. Если хотя бы половина будет интересной по содержанию, то этого вполне хватит на приличный фотоальбомчик.
Пределы применимости?
Рассмотренная логика вывода перестаёт работать на экспозициях, при которых объект съёмки несколько раз меняет скорость и направление движения. Для танца это субсекундные экспозиции. Верен ли вывод за их пределом? Некоторые интуитивные соображения и неравенство Бернштейна-Колмогорова вроде бы указывают, что степенное масштабирование O(1/dtk) сохранится и на больших выдержках. Но я не берусь это сейчас со всей строгостью доказать.
Замечание 1. Разумеется, успех фотографии зависит от огромного количества факторов, помимо смаза изображения. И многие из них — скажем, неравномерная освещённость помещения, или малая глубина резкости при съёмке — вполне способны «убить» как снимок (в техническом смысле), так и выписанную выше зависимость. Тем не менее, на практике она работает достаточно неплохо. Впервые что-то похожнее на p(чёткость) ≈ 1/dt2 я намерял в 2009-с году. С тех пор были сделаны сотни тысяч кадров, многие — при рискованных экспозициях, и результаты в целом соответствовали ожиданиям, проистекающим из этой формулы.
Замечание 2. Конечно, сегодня этот результат менее важен, чем 10-20 лет назад, когда максимальная рабочая чувствительность камеры могла составлять лишь 400-800 ISO, и приходилось идти на дикие ухищрения, дабы поймать один приличный снимок в полутьме. Сегодня (или в скором будущем) эту задачу вполне может решить софт. Снять видео на ISO в 12800, задетектировать глаза, и выбрать из сотен фреймов один-единственный с наилучшим качеством. Многие навыки, добывавшиеся десятилетиями практики, отходят сегодня автоматике. И это, наверное, правильно.
Спасибо и хороших всем кадров!
Автор: Евгений Бобух


