Всем привет!
Меня зовут Алексей. Я Data Scientist в компании Align Technology. В этом материале я расскажу вам о подходах к feature selection, которые мы практикуем в ходе экспериментов по анализу данных.
В нашей компании статистики и инженеры machine learning анализируют большие объемы клинической информации, связанные с лечением пациентов. В двух словах смысл этой статьи можно свести к извлечению ценных крупиц знания, содержащихся в небольшой доле доступных нам зашумленных и избыточных гигабайтов данных.
Данная статья предназначена для статистиков, инженеров машинного обучения и специалистов, которые интересуются вопросами обнаружения зависимостей в наборах данных. Также материал, изложенный в статье, может быть интересен широкому кругу читателей, неравнодушных к data mining. В материале не будут затронуты вопросы feature engineering и, в частности, применения таких методов как анализ главных компонент.
Установлено, что наборы с большим количеством входных переменных могут содержать избыточную информацию и ведут к переобученности моделей машинного обучения в том случае, если в модели не встроен регуляризатор. Стадия отбора информативных признаков (ОИП здесь и далее) часто является необходимым шагом в предобработке данных в ходе эксперимента.
- В первой части данной статьи мы сделаем обзор некоторых методов отбора признаков и рассмотрим теоретические моменты в этом процессе. Данный раздел является скорее систематизацией наших взглядов.
- Во второй части статьи на примере искусственного набора данных мы поэкспериментируем с отбором информативных признаков и сделаем сравнение результатов.
- В третьей части мы осветим теорию и практику использования мер из теории информации в применении к обсуждаемой задаче. Метод, представленный в этом разделе, обладает новизной, однако он, по-прежнему, требует проведения многочисленных проверок на различных наборах данных.
Эксперименты, проведенные в статье, не претендуют на научную законченность в силу того, что аналитические обоснования оптимальности того или иного метода приведены не будут, и читатель отсылается к первоисточникам за более подробным и математически точным изложением. Помимо этого, disclaimer состоит в том, что на других данных ценность того или иного метода поменяется, что и делает задачу в целом интеллектуально привлекательной.
В конце статьи будут сведены результаты экспериментов и сделана ссылка на полный код R на Git.
Я выражаю благодарность всем людям, прочитавшим материал до публикации и сделавшим его лучше, в частности, Владу Щербинину и Алексею Селезневу.
1) Способы и методы отбора информативных признаков.
Давайте рассмотрим общий подход к классификации методов ОИП, обратившись к Вики:
Алгоритмы отбора информативных признаков могут быть представлены следующими группами: Wrappers (оберточные), Filters (фильтровочные) и Embedded (встроенные в машины). (Я оставлю без точного перевода эти термины в виду размытости их звучания для русскоязычного сообщества — прим. мое.)
Оберточные алгоритмы создают поднаборы, используя поиск в пространстве возможных входных переменных и оценивают полученные поднаборы входов путем обучения полной модели на имеющихся данных. Оберточные алгоритмы могут быть очень дорогими и рискуют переобучать модель. (Если не используется валидационная выборка — прим. мое.)
Фильтровочные алгоритмы похожи на оберточные в том, что они также выполняют поиск поднаборов входных данных, но, вместо запуска полной модели, важность поднабора для выходной переменной оценивается с помощью более простого (фильтровочного) алгоритма.
Встроенные в машины алгоритмы оценивают важность входных признаков с помощью эвристики, заранее заложенной в обучение.
Примеры.
Оберточным алгоритмом ОИП можно назвать комбинацию методов, включающую поиск поднабора входных переменных с последующим обучением, например, random forest, на отобранных данных и оценкой его ошибки на кроссвалидации. То есть для каждой итерации мы будем обучать целую машину (уже фактически готовую к дальнейшему использованию).
Фильтровочным алгоритмом ОИП можно назвать перебор входных переменных, дополняемый проведением статистического теста на зависимость между отобранными переменными и выходом. Если наши входы и выход категориальны, то возможно провести тест хи-квадрат на независимость между входом (или комбинированным набором входов) и выходом с оценкой p-value и, как следствие, бинарным выводом о значимости или незначимости отобранного набора признаков. Другими примерами фильтровочных алгоритмов можно считать:
- линейную корреляцию входа и выхода;
- статистический тест на разницу в средних в случае категориальных входов и непрерывного выхода;
- F-критерий (дисперсионный анализ).
Встроенным алгоритмом ОИП является, например, значения p-values, соответствующие коэффициентам линейной регрессии. В данном случае p-value позволяет также сделать бинарный вывод о значимом отличиии коэффициента от нуля. Если отмасштабировать все входы модели, то модули весов можно трактовать как показатели важности. Также можно использовать R^2 модели — меру объяснения дисперсии процесса смоделированными значениями. Еще одним примером может служить функция оценки важности входных переменных, встроенная в random forest. Кроме того, можно использовать модули весов, соответствующие входам в искуственной нейронной сети. Этим список не исчерпывается.
На этом этапе важно понять, что это разграничение, по сути, указывает на различие фитнесс-функций ОИП, то есть меры релевантности найденного поднабора входных признаков по отношению к решаемой задаче. Впоследствии мы еще вернемся к вопросу выбора фитнесс-функции.
Теперь, когда мы немного ориентируемся в основных группах методов ОИП, предлагаю обратить внимание на то, какими методами осуществляется именно перебор поднаборов входных переменных. Снова обратимся к странице Вики:
Подходы к перебору включают:
- Полный перебор
- Первый лучший кандидат
- Имитация отжига
- Генетический алгоритм
- Жадный поиск на включение
- Жадный поиск на исключение
- Particle swarm optimization
- Targeted projection pursuit
- Scatter Search
- Variable Neighborhood Search
Я умышленно не стал переводить названия некоторых алгоритмов, так как не знаком с их русскоязычной интерпретацией.
Поиск поднабора предикторов — это дискретная задача, так как на выходе мы получаем вектор целых чисел, обозначающих индексы входов, вида:
входы: 1 2 3 4 5 6… 1000
отбор: 0 0 1 1 1 0… 1
Мы вернемся к этой особенности позднее и проиллюстрируем, к чему она ведет практически.
От того, как будет настроен поиск поднабора входных признаков, сильно зависит результат всего эксперимента. Для того чтобы интуитивно понять основное отличие в этих подходах, я предлагаю читателю поделить их на две группы: жадные (greedy) и нежадные (non-greedy).
Жадные алгоритмы поиска.
Они используются часто, так как быстры и дают хороший результат во многих задачах. Жадность алгоритма заключается в том, что если был выбран (или исключен) один из кандидатов на вхождение в финальный поднабор, в дальнейшем он в нем остается (в случае жадного включения) или навсегда отсутствует (в случае жадного исключения). Таким образом, если на ранних итерациях был выбран кандидат А, на поздних итерациях поднабор всегда будет включать его и других кандидатов, которые вместе с А показывают улучшение метрики важности поднабора для выходной переменной. Обратная ситуация для исключения: если был убран кандидат А, потому что после его исключения метрика важности наименее пострадала или улучшилась, исследователь не получит информации о метрике важности, где в поднаборе есть А и другие, исключенные позже кандидаты.
Если проводить параллель с поиском максимума (минимума) в многомерном пространстве, жадный алгоритм будет застревать в локальном минимуме, если такой есть, либо быстро находить оптимальное решение, если есть единственный минимум, и он глобален.
С другой стороны, перебор всех жадных вариантов осуществляется относительно быстро и позволяет учесть некоторые взаимодействия между входами.
Примеры жадных алгоритмов: жадное включение (forward selection; step forward) и жадное исключение (backward elimination; step backward). На этом список не ограничивается.
Нежадные алгоритмы поиска.
Принцип работы нежадных алгоритмов подразумевает возможность отбросить целиком или частично сформированные поднаборы признаков, комбинации поднаборов между собой и внести случайные изменения в поднаборы с целью избежания локального минимума.
Если провести аналогию с поиском максимума (минимума) значения фитнесс-функции в многомерном пространстве, нежадные алгоритмы рассматривают гораздо больше соседних точек и даже могут совершать большие скачки в случайные области.
Можно представить графически работу этих видов алгоритмов.
Сначала жадное включение:
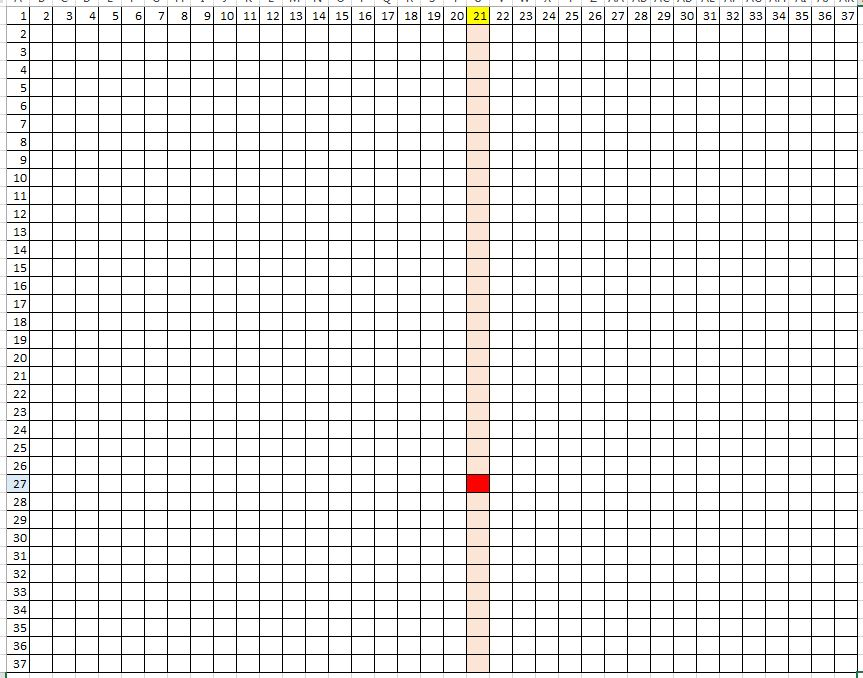
Теперь нежадный — стохастический — поиск:
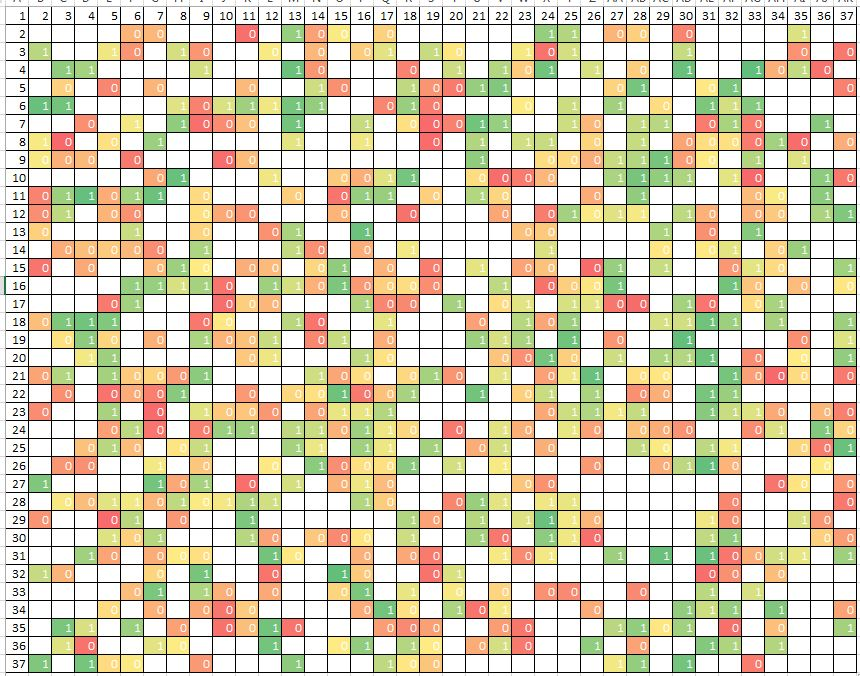
В обоих случаях нужно отобрать одну самую лучшую комбинацию из двух входов, чьи индексы отложены по осям графика. Жадный алгоритм начинает с того, что отбирает один лучший вход, перебирая индексы по горизонтали. А затем добавляет к отобранному входу второй вход так, чтобы их суммарная релевантность была максимальна. Но получается, что из все возможных комбинаций он полностью проходит только 1/37 часть. При добавлении еще одного измерения, количество пройденных ячеек станет еще меньше: примерно, 1/37^2.
При этом возможна практическая ситуация, когда лучшей является не та комбинация, которую нашел жадный алгоритм. Это может произойти, если каждый из двух входов по отдельности не показывает лучшую релевантность задаче (и они не будут отобраны на первом шаге), но их взаимодействие максимизирует метрику релевантности.
Нежадный алгоритм ищет гораздо дольше:
(O) = 2^n
и проверяет больше воможных комбинаций входов. Но он имеет шанс найти, возможно, еще более хороший поднабор входов благодаря размашистому поиску сразу во всех изменениях задачи.
Есть алгоритмы поиска, выходящие за рамки установленной дихотомии жадный / нежадный.
Примером такого обособленного поиска будет являться поочередный перебор входов по отдельности и оценка их отдельной важности для выходной переменной. С этого, кстати, начинается первая волна в алгоритме жадного включения переменных. Но что же получается хорошего с таким перебором, за исключением того, что он очень быстрый? Каждая входная переменная начинает существовать «в вакууме», то есть без учета влияния других входов на связь между выбранным входом и выходом. При этом, после завершения работы алгоритма получившийся список входов с указанием их индивидуальной важности для выхода всего лишь дает информацию об индивидуальной значимости каждого предиктора. При объединении некоторого количества самых важных предикторов, согласно такому списку, можно получить ряд проблем:
- избыточность (в случае корреляции предикторов между собой);
- недостаточность информации из-за неучета взаимодействий предикторов на этапе отбора;
- размытость границы, выше которой нужно взять предикторы.
Как можно видеть, проблемы не самые тривиальные.
Основной вопрос в задаче ОИП формулируется как оптимальная комбинация метода поиска поднабора и фитнесс-функции.
Рассмотрим подробнее это утверждение. Наша задача ОИП может быть описана двумя гипотезами:
а) поверхность ошибки простая или сложная;
б) в данных есть простые зависимости или сложные.
В зависимости от ответов на эти вопросы следует остановить выбор на конкретной связке метода поиска и метода определения релевантности отобранных признаков.
Поверхность ошибки.
Пример несложной поверхности:
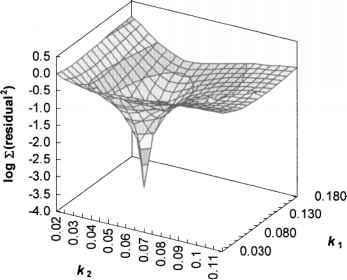
Здесь мы выбираем комбинацию из двух входов, определяя их релевантность выходу и спускаемся по плавной поверхности в направлении градиента, почти наверное попадая в точку оптимума.
Пример сложной поверхности:
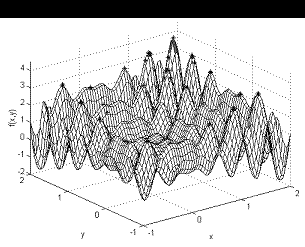
В этом случае, решая ту же задачу, мы встречаемся с множеством локальных минимумов, выбраться из которых жадный алгоритм не сможет. В то же время, алгоритм со стохастическим поиском имеем повышенный шанс найти более точное решение.
Ранее мы упомянули, что поиск поднабора предикторов — это дискретная задача. Если зависимость выхода от входов включает в себя взаимодействия, при при переходе из одной точки пространства в соседнюю можно наблюдать резкие скачки значения фитнесс-функции. Поверхность ошибки в нашем случае часто не гладкая, не дифференцируемая:
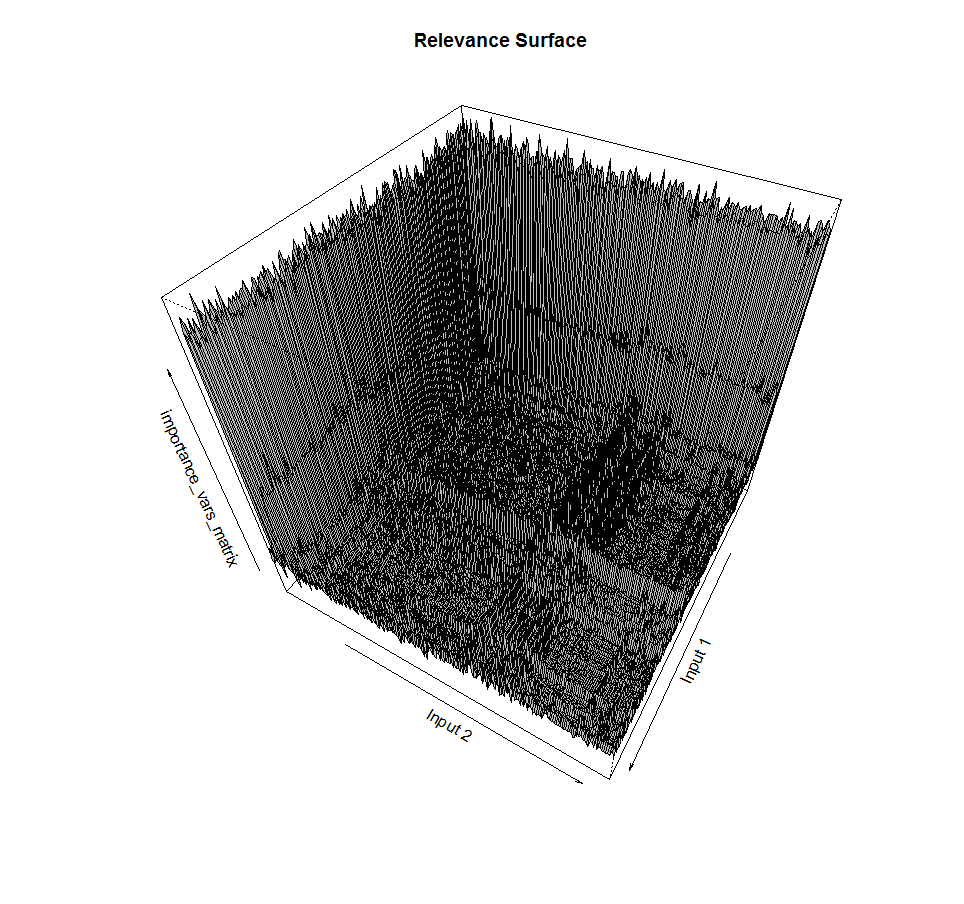
Это пример поиска поднабора из двух входов и соответствующее значение функции релевантности поднабора выходной переменной. Видно, что поверхность далеко не гладкая, с пиками, а также включает в себя изрезанные плато примерно одинаковых значений. Ночной кошмар для методов жадного градиентного спуска.
Зависимости.
С ростом числа измерений задачи повышается теоретичекий шанс того, что зависимость выходной переменной имеет весьма сложную структуру и задействует множество входов. Кроме того, завимость может иметь как линейный вид, так и быть нелинейной. Если зависимость подразумевает взаимодействие предикторов и нелинейный вид, найти ее можно будет, только учитывая оба эти момента, применив, например, обучение random forest или нейронную сеть. Если зависимость простая, линейная, включает в себя только небольшую часть из всех предикторов, подход к ее нахождению — и, как следствие, к ОИП, — можно свести к поочередному включению в модель линейной регрессии по 1 или несколько входов с оценкой качества модели.
Пример простой зависимости:
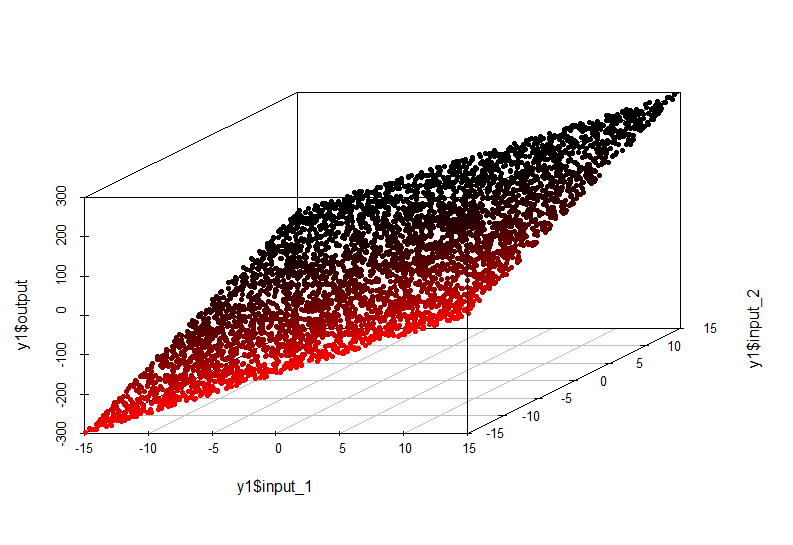
В данном случае зависимость значения по оси output от значений input1 и input2 описывается плоскостью в пространстве:
output = input1*10 + input2*10
Модель такой зависимости очень простая и может быть аппроксимирована линейной регрессией.
Пример сложной зависимости:
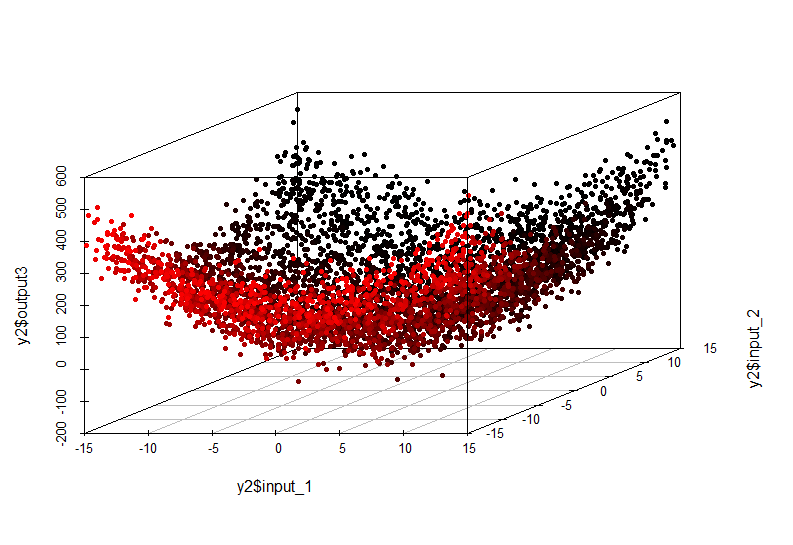
Эта нелинейная зависимость уже не может быть выявлена построением линейной модели. Ее вид таков:
output = input1^2 + input2^2
Также необходимо учесть размерность задачи.
Если количество входных переменных велико, поиск оптимального поднабора стохастическими методами (нежадными) может быть очень дорогим в силу того, что общее количество всех возможных поднаборов задается отношением
m = 2 ^ n,
где n — количество всех входных признаков.
Соответственно, поиск минимума в таком многообразии может быть очень долог. С другой стороны, применение жадного поиска позволит сделать первое приближение за разумное время, даже если это будет локальным минимумом и исследователь будет знать об этом.
В условиях отсутствия предметного знания об изучаемом явлении невозможно заранее сказать, насколько сложной будет зависимость входных переменных и выхода и какое количество входов будет оптимально для нахождения приближенного или точного решения задачи отбора оптимального поднабора входов. Также затруднительно предсказать, будет ли поверхность ошибки при ОИП гладкой и простой или сложной и изрезанной.
Также мы всегда ограничены в ресурсах и должны принимать наиболее оптимальные решения. В качестве небольшой помощи при выработке подхода к ОИП можно использовать следующую таблицу:

Таким образом, у нас всегда есть возможность рассмотреть несколько комбинаций методов поиска поднабора входов и фитнесс-функции релевантности. Самая дорогая и, наверное, наиболее эффективная комбинация — это жадный поиск и оберточная (wrapper) фитнесс-фукнция. Позволяет избегать локального минимума, при этом предоставляя наиболее точную меру релевантности отобранных входов, так как на каждой итерации есть обученная модель (и ее точность на валидации).
Наименее дорогой, но не всегда наимее эффективный подход, это жадный поиск в паре с фильтровочной (filter) функцией, которая может быть статистическим тестом, коэффициентом корреляции или количеством взаимной информации.
Кроме того, встроенные (embedded) методы позволяют сразу после обучения модели отсеять ряд ненужных с точки зрения алгоритма входов, не потеряв существенно в точности моделирования.
Хорошим тоном будет попытка несколько раз решить задачу разными способами и выбрать наилучший.
В общем говоря, отбор информативных признаков — это подбор лучшей комбинации метода поиска в многомерном пространстве и наиболее оптимальной фитнесс-функции релевантности отобранного поднабора по отношению к выходной переменной.

2) Эксперименты по отбору информативных признаков на синтетических данных.
Наш подопытный набор данных («Стэнфордский кролик»):

Просто я люблю кроликов.
Мы будем смотреть на зависимость высоты точки (ось Z) от широты и долготы. При этом в набор я добавляю 10 шумовых переменных с распределением примерно соответствующим смеси двух информативных входов (X и Y), но никак не связанных с переменной Z.
Посмотрим на гистограммы плотности распределения для переменных X, Y, Z и одной из шумовых переменных.
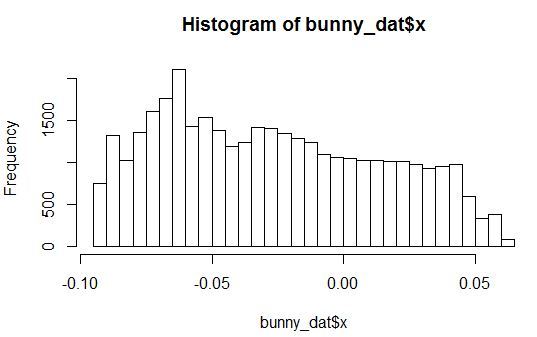
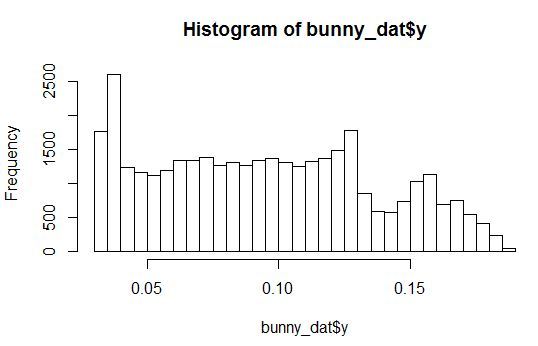
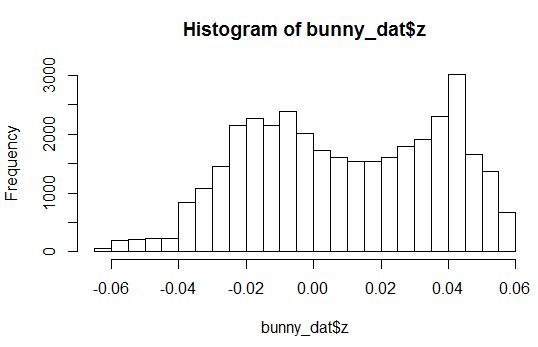
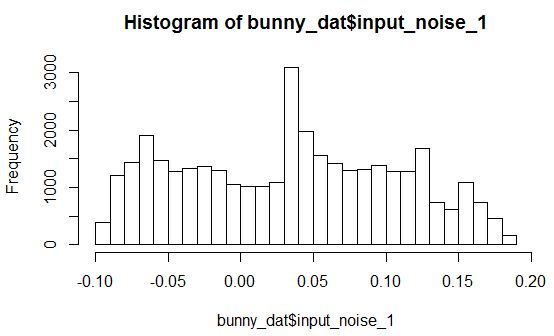
Видно, что распределения с произвольными параметрами. При этом все шумовые переменные распределены так, что у них есть небольшой пик в некоторой области значений.
Далее набор данных будет случайно поделен на две части: обучение и валидация.
Подготовка данных.
library(onion)
data(bunny)
#XYZ point plot
open3d()
points3d(bunny, col=8, size=0.1)
bunny_dat <- as.data.frame(bunny)
inputs <- append(as.numeric(bunny_dat$x),
as.numeric(bunny_dat$y))
for (i in 1:10){
naming <- paste('input_noise_', i, sep = '')
bunny_dat[, eval(naming)] <- inputs[sample(length(inputs), nrow(bunny_dat), replace = T)]
}
Эксперимент №1: жадный поиск поднабора входов с линейной функцией оценки важности (в качестве фитнесс-функции будет использоваться вариант wrapper — оценка коэффициента детерминации обученной модели на валидационной выборке).
### greedy search with filter function
library(FSelector)
sampleA <- bunny_dat[sample(nrow(bunny_dat), nrow(bunny_dat) / 2, replace = F), c("x",
"y",
"input_noise_1",
"input_noise_2",
"input_noise_3",
"input_noise_4",
"input_noise_5",
"input_noise_6",
"input_noise_7",
"input_noise_8",
"input_noise_9",
"input_noise_10",
"z")]
sampleB <- bunny_dat[!row.names(bunny_dat) %in% rownames(sampleA), c("x",
"y",
"input_noise_1",
"input_noise_2",
"input_noise_3",
"input_noise_4",
"input_noise_5",
"input_noise_6",
"input_noise_7",
"input_noise_8",
"input_noise_9",
"input_noise_10",
"z")]
linear_fit <- function(subset){
dat <- sampleA[, c(subset, "z")]
lm_m <- lm(formula = z ~.,
data = dat,
model = T)
lm_predict <- predict(lm_m,
newdata = sampleB)
r_sq_validate <- 1 - sum((sampleB$z - lm_predict) ^ 2) / sum((sampleB$z - mean(sampleB$z)) ^ 2)
print(subset)
print(r_sq_validate)
return(r_sq_validate)
}
#subset <- backward.search(attributes = names(sampleA)[1:(ncol(sampleA) - 1)], eval.fun = linear_fit)
subset <- forward.search(attributes = names(sampleA)[1:(ncol(sampleA) - 1)], eval.fun = linear_fit)
Результат:
> subset
<b>[1] "x" "y" "input_noise_2" "input_noise_5" "input_noise_6" "input_noise_8" "input_noise_9"</b>
Оказались включены шумовые переменные.
Посмотрим на обученную модель:
> summary(lm_m)
Call:
lm(formula = z ~ ., data = dat, model = T)
Residuals:
Min 1Q Median 3Q Max
-0.060613 -0.022650 -0.000173 0.024939 0.048544
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.0232453 0.0005581 41.651 < 2e-16 ***
<b>x -0.0257686 0.0052998 -4.862 1.17e-06 ***
y -0.1572786 0.0052585 -29.910 < 2e-16 ***</b>
input_noise_2 -0.0017249 0.0027680 -0.623 0.533
input_noise_5 -0.0027391 0.0027848 -0.984 0.325
input_noise_6 0.0032417 0.0027907 1.162 0.245
input_noise_8 0.0044998 0.0027723 1.623 0.105
input_noise_9 0.0006839 0.0027808 0.246 0.806
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.02742 on 17965 degrees of freedom
Multiple R-squared: 0.04937, Adjusted R-squared: 0.049
F-statistic: 133.3 on 7 and 17965 DF, p-value: < 2.2e-16
Видим, что на самом деле статистическую значимость принимают только наши оригинальные входы и свободный член уравнения.
А теперь проведем жадное исключение переменных.
subset <- backward.search(attributes = names(sampleA)[1:(ncol(sampleA) - 1)], eval.fun = linear_fit)
#subset <- forward.search(attributes = names(sampleA)[1:(ncol(sampleA) - 1)], eval.fun = linear_fit)
Результат:
> subset
<b>[1] "x" "y" "input_noise_2" "input_noise_5" "input_noise_6" "input_noise_8" "input_noise_9"</b>
Модель также включила шумы.
Посмотрим на обученную модель:
> summary(lm_m)
Call:
lm(formula = z ~ ., data = dat, model = T)
Residuals:
Min 1Q Median 3Q Max
-0.060613 -0.022650 -0.000173 0.024939 0.048544
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.0232453 0.0005581 41.651 < 2e-16 ***
<b>x -0.0257686 0.0052998 -4.862 1.17e-06 ***
y -0.1572786 0.0052585 -29.910 < 2e-16 ***</b>
input_noise_2 -0.0017249 0.0027680 -0.623 0.533
input_noise_5 -0.0027391 0.0027848 -0.984 0.325
input_noise_6 0.0032417 0.0027907 1.162 0.245
input_noise_8 0.0044998 0.0027723 1.623 0.105
input_noise_9 0.0006839 0.0027808 0.246 0.806
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.02742 on 17965 degrees of freedom
Multiple R-squared: 0.04937, Adjusted R-squared: 0.049
F-statistic: 133.3 on 7 and 17965 DF, p-value: < 2.2e-16
Аналогично, внутри модели видим, что важны только оригинальные входы.
Если же мы обучим модель только на переменных X и Y, мы получим:
> print(subset)
<b>[1] "x" "y"</b>
> print(r_sq_validate)
<b>[1] 0.05185492</b>
> summary(lm_m)
Call:
lm(formula = z ~ ., data = dat, model = T)
Residuals:
Min 1Q Median 3Q Max
-0.059884 -0.022653 -0.000209 0.024955 0.048238
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.0233808 0.0005129 45.590 < 2e-16 ***
<b>x -0.0257813 0.0052995 -4.865 1.15e-06 ***
y -0.1573098 0.0052576 -29.920 < 2e-16 ***</b>
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.02742 on 17970 degrees of freedom
Multiple R-squared: 0.04908, Adjusted R-squared: 0.04898
F-statistic: 463.8 on 2 and 17970 DF, p-value: < 2.2e-16
Дело в том, что на валидации R^2 был повыше тогда, когда выключены шумовые переменные.
Странный результат! Наверное, из-за структуры данных шумы не оказывают пагубного влияния на модель.
Но мы еще не попробовали учесть взаимодействие предикторов.
lm_m <- lm(formula = z ~ x * y,
data = dat,
model = T)
> summary(lm_m)
Call:
lm(formula = z ~ x * y, data = dat, model = T)
Residuals:
Min 1Q Median 3Q Max
-0.057761 -0.023067 -0.000119 0.024762 0.049747
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.0196766 0.0006545 30.062 <2e-16 ***
x -0.1513484 0.0148113 -10.218 <2e-16 ***
y -0.1084295 0.0075183 -14.422 <2e-16 ***
x:y 1.3771299 0.1517363 9.076 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.02736 on 17969 degrees of freedom
Multiple R-squared: 0.05342, Adjusted R-squared: 0.05327
F-statistic: 338.1 on 3 and 17969 DF, p-value: < 2.2e-16
Получилось неплохо. Взамодействие X и Y значимо. А что насчет R^2 на валидации?
> lm_predict <- predict(lm_m,
+ newdata = sampleB)
> 1 - sum((sampleB$z - lm_predict) ^ 2) / sum((sampleB$z - mean(sampleB$z)) ^ 2)
<b>[1] 0.05464066</b>
Это самое высокое значение, из тех, что мы видели. К сожалению, именно вариант взаимодействия не был заложен в фитнесс-функцию и мы пропустили эту комбинацию входов.
Эксперимент №2: жадный поиск поднабора входов с линейной функцией оценки важности (в качестве фитнесс-функции будет использоваться вариант embedded — f-статистика обученной модели на обучающей выборке).
linear_fit_f <- function(subset){
dat <- sampleA[, c(subset, "z")]
lm_m <- lm(formula = z ~.,
data = dat,
model = T)
print(subset)
print(summary(lm_m)$fstatistic[[1]])
return(summary(lm_m)$fstatistic[[1]])
}
#subset <- backward.search(attributes = names(sampleA)[1:(ncol(sampleA) - 1)], eval.fun = linear_fit_f)
subset <- forward.search(attributes = names(sampleA)[1:(ncol(sampleA) - 1)], eval.fun = linear_fit_f)
Результат последовательного включения переменных — только один предиктор Y. Для него максимизировалась F-Statistic. То есть это переменная очень важна. Но почему-то забыта переменная X.
А теперь последовательное исключение переменных.
Результат аналогичен — только одна переменная Y.
Можно отметить, что при максимизации F-Statistic многопеременной модели все шумы оказались за бортом, и модель при этом получилась робастной: на валидации коэффициент детерминации почти не уступает лучшей модели из эксперимента №1:
> r_sq_validate
<b>[1] 0.05034534</b>
Эксперимент №3: поочередная оценка индивидуальной значимости предикторов с помощью коэффициент корреляции Пирсона (этот вариант наиболее простой, он не учитывает взаимодействия, фитнесс-функция также простая — оценивает только линейную связь).
correlation_arr <- data.frame()
for (i in 1:12){
correlation_arr[i, 1] <- colnames(sampleA)[i]
correlation_arr[i, 2] <- cor(sampleA[, i], sampleA[, 'z'])
}
Результат:
> correlation_arr
V1 V2
<b>1 x 0.0413782832
2 y -0.2187061876</b>
3 input_noise_1 -0.0097719425
4 input_noise_2 -0.0019297383
5 input_noise_3 0.0002143946
6 input_noise_4 -0.0142325764
7 input_noise_5 -0.0048206943
8 input_noise_6 0.0090877674
9 input_noise_7 -0.0152897433
10 input_noise_8 0.0143477495
11 input_noise_9 0.0027560459
12 input_noise_10 -0.0079526578
Наибольшая корреляция Z с Y, и на втором месте — X. Однако корреляция X не явно выражена и требует проведение статистического теста на значимость отличия коэффициента корреляции от нуля для каждой из переменных.
С другой стороны, во всех проведенных 3-х экспериментах мы вообще не учитывали взаимодействие предикторов (X * Y). Этим можно объяснить то, что оценка единичной значимости или линейное включение предикторов в уравнение не дает нам однозначного ответа.
Такой экспериментик:
> cor(sampleA$x * sampleA$y, sampleA$z)
<b>[1] 0.1211382</b>
Показывает, что взаимодействие X и Y коррелирует с Z довольно сильно.
Эксперимент №4: оценка важности предикторов встроенным в машину алгоритмом (вариант жадного поиска и embedded фитнесс-функции важности входов в GBM).
Обучим Gradient Boosted Trees (gbm) и посмотрим на важность переменных. Хорошая статья, детально описывающая аспекты применения GBM: Gradient boosting machines, a tutorial.
Возьмем параметры обучения с потолка, установим очень низкую скорость обучения, чтобы избежать сильного переобучения. Заметим, что любые деревья решений жадны, а улучшение модели путем добавления многих моделей достигается сэмплированием наблюдений и входов.
library(gbm)
gbm_dat <- bunny_dat[, c("x",
"y",
"input_noise_1",
"input_noise_2",
"input_noise_3",
"input_noise_4",
"input_noise_5",
"input_noise_6",
"input_noise_7",
"input_noise_8",
"input_noise_9",
"input_noise_10",
"z")]
gbm_fit <- gbm(formula = z ~.,
distribution = "gaussian",
data = gbm_dat,
n.trees = 500,
interaction.depth = 12,
n.minobsinnode = 100,
shrinkage = 0.0001,
bag.fraction = 0.9,
train.fraction = 0.7,
n.cores = 6)
gbm.perf(object = gbm_fit,
plot.it = TRUE,
oobag.curve = F,
overlay = TRUE)
summary(gbm_fit)
Результат:
> summary(gbm_fit)
var rel.inf
<b>y y 69.7919
x x 30.2081</b>
input_noise_1 input_noise_1 0.0000
input_noise_2 input_noise_2 0.0000
input_noise_3 input_noise_3 0.0000
input_noise_4 input_noise_4 0.0000
input_noise_5 input_noise_5 0.0000
input_noise_6 input_noise_6 0.0000
input_noise_7 input_noise_7 0.0000
input_noise_8 input_noise_8 0.0000
input_noise_9 input_noise_9 0.0000
input_noise_10 input_noise_10 0.0000
Этот подход великолепно справился с поставленной задачей и выделил нешумовые входы, сделав все остальные входы абсолютно незначимыми.
Причем, нужно заметить, что настройка данного эксперимента очень быстрая, все работает практически «из коробки». Более тщательное планирование данного эксперимента, включая кроссвалидацию для получения оптимальных параметров обучения, — дело более сложное, но при подготовке реальной модели в production сделать это необходимо.
Эксперимент №5: оценка важности предикторов, используя стохастический поиск с линейной функцией оценки важности (это нежадный поиск в пространстве входов, а в качестве фитнесс-функции будет использоваться вариант wrapper — оценка коэффициента детерминации обученной модели на валидационной выборке).
В этот раз обучающаяся линейная модель включает попарные взаимодействия между предикторами.
### simulated annealing search with linear model interactions stats
library(scales)
library(GenSA)
sampleA <- bunny_dat[sample(nrow(bunny_dat), nrow(bunny_dat) / 2, replace = F), c("x",
"y",
"input_noise_1",
"input_noise_2",
"input_noise_3",
"input_noise_4",
"input_noise_5",
"input_noise_6",
"input_noise_7",
"input_noise_8",
"input_noise_9",
"input_noise_10",
"z")]
sampleB <- bunny_dat[!row.names(bunny_dat) %in% rownames(sampleA), c("x",
"y",
"input_noise_1",
"input_noise_2",
"input_noise_3",
"input_noise_4",
"input_noise_5",
"input_noise_6",
"input_noise_7",
"input_noise_8",
"input_noise_9",
"input_noise_10",
"z")]
#calculate parameters
predictor_number <- dim(sampleA)[2] - 1
sample_size <- dim(sampleA)[1]
par_v <- runif(predictor_number, min = 0, max = 1)
par_low <- rep(0, times = predictor_number)
par_upp <- rep(1, times = predictor_number)
############### the fitness function
sa_fit_f <- function(par){
indexes <- c(1:predictor_number)
for (i in 1:predictor_number){
if (par[i] >= threshold) {
indexes[i] <- i
} else {
indexes[i] <- 0
}
}
local_predictor_number <- 0
for (i in 1:predictor_number){
if (indexes[i] > 0) {
local_predictor_number <- local_predictor_number + 1
}
}
if (local_predictor_number > 0) {
sampleAf <- as.data.frame(sampleA[, c(indexes[], dim(sampleA)[2])])
lm_m <- lm(formula = z ~ .^2,
data = sampleAf,
model = T)
lm_predict <- predict(lm_m,
newdata = sampleB)
r_sq_validate <- 1 - sum((sampleB$z - lm_predict) ^ 2) / sum((sampleB$z - mean(sampleB$z)) ^ 2)
} else {
r_sq_validate <- 0
}
return(-r_sq_validate)
}
#stimating threshold for variable inclusion
threshold <- 0.5 # do it simply
#run feature selection
start <- Sys.time()
sao <- GenSA(par = par_v, fn = sa_fit_f, lower = par_low, upper = par_upp
, control = list(
#maxit = 10
max.time = 300
, smooth = F
, simple.function = F))
trace_ff <- data.frame(sao$trace)$function.value
plot(trace_ff, type = "l")
percent(- sao$value)
final_vector <- c((sao$par >= threshold), T)
names(sampleA)[final_vector]
final_sample <- as.data.frame(sampleA[, final_vector])
Sys.time() - start
# check model
lm_m <- lm(formula = z ~ .^2,
data = sampleA[, final_vector],
model = T)
summary(lm_m)
Что-же получилось?
<b>[1] "5.53%"</b>
> final_vector <- c((sao$par >= threshold), T)
> names(sampleA)[final_vector]
<b>[1] "x" "y" "input_noise_7" "input_noise_8" "input_noise_9" "z" </b>
> summary(lm_m)
Call:
lm(formula = z ~ .^2, data = sampleA[, final_vector], model = T)
Residuals:
Min 1Q Median 3Q Max
-0.058691 -0.023202 -0.000276 0.024953 0.050618
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.0197777 0.0007776 25.434 <2e-16 ***
<b>x -0.1547889 0.0154268 -10.034 <2e-16 ***
y -0.1148349 0.0085787 -13.386 <2e-16 ***</b>
input_noise_7 -0.0102894 0.0071871 -1.432 0.152
input_noise_8 -0.0013928 0.0071508 -0.195 0.846
input_noise_9 0.0026736 0.0071910 0.372 0.710
<b>x:y 1.3098676 0.1515268 8.644 <2e-16 ***</b>
x:input_noise_7 0.0352997 0.0709842 0.497 0.619
x:input_noise_8 0.0653103 0.0714883 0.914 0.361
x:input_noise_9 0.0459939 0.0716704 0.642 0.521
y:input_noise_7 0.0512392 0.0710949 0.721 0.471
y:input_noise_8 0.0563148 0.0707809 0.796 0.426
y:input_noise_9 -0.0085022 0.0710267 -0.120 0.905
input_noise_7:input_noise_8 0.0129156 0.0374855 0.345 0.730
input_noise_7:input_noise_9 0.0519535 0.0376869 1.379 0.168
input_noise_8:input_noise_9 0.0128397 0.0379640 0.338 0.735
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.0274 on 17957 degrees of freedom
Multiple R-squared: 0.05356, Adjusted R-squared: 0.05277
F-statistic: 67.75 on 15 and 17957 DF, p-value: < 2.2e-16
Видно, что мы промахиваемся. Включены шумы.
Как видим, лучшее значение коэффициента детерминации на валидации достигнут с включением шумовых переменных. При этом сходимость алгоритма поиска исчерпывающая:
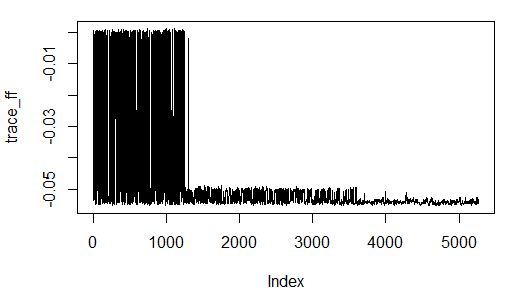
Попробуем поменять фитнесс-функцию, сохраним метод поиска.
Эксперимент №6: оценка важности предикторов, используя стохастический поиск с линейной функцией оценки важности (это нежадный поиск в пространстве входов, фитнесс-функция — embedded p-values, соответствующие коэффициентам модели).
Мы будем отбирать такой набор предикторов, у которых минимизируется среднее значение p-value у входящих в модель коэффициентов.
# fittness based on p-values
sa_fit_f2 <- function(par){
indexes <- c(1:predictor_number)
for (i in 1:predictor_number){
if (par[i] >= threshold) {
indexes[i] <- i
} else {
indexes[i] <- 0
}
}
local_predictor_number <- 0
for (i in 1:predictor_number){
if (indexes[i] > 0) {
local_predictor_number <- local_predictor_number + 1
}
}
if (local_predictor_number > 0) {
sampleAf <- as.data.frame(sampleA[, c(indexes[], dim(sampleA)[2])])
lm_m <- lm(formula = z ~ .^2,
data = sampleAf,
model = T)
mean_val <- mean(summary(lm_m)$coefficients[, 4])
} else {
mean_val <- 1
}
return(mean_val)
}
#stimating threshold for variable inclusion
threshold <- 0.5 # do it simply
#run feature selection
start <- Sys.time()
sao <- GenSA(par = par_v, fn = sa_fit_f2, lower = par_low, upper = par_upp
, control = list(
#maxit = 10
max.time = 60
, smooth = F
, simple.function = F))
trace_ff <- data.frame(sao$trace)$function.value
plot(trace_ff, type = "l")
percent(- sao$value)
final_vector <- c((sao$par >= threshold), T)
names(sampleA)[final_vector]
final_sample <- as.data.frame(sampleA[, final_vector])
Sys.time() - start
Результат:
> percent(- sao$value)
<b>[1] "-4.7e-208%"</b>
> final_vector <- c((sao$par >= threshold), T)
> names(sampleA)[final_vector]
<b>[1] "y" "z"</b>
В этот раз все получилось. Были отобраны только оригинальные предикторы, так как их p-values действительно малы.
Сходимость алгоритма хорошая за 60 секунд:
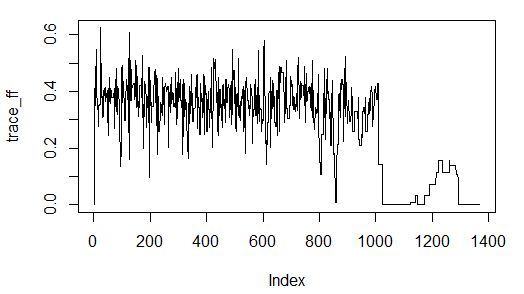
Эксперимент №7: оценка важности предикторов, используя жадный поиск с оценкой важности по качеству обученной модели (это жадный поиск в пространстве входов, фитнесс-функция — wrapper, соответствующий коэффициенту детерминации на валидации модели boosted decision trees).
### greedy search with wrapper GBM validation fitness
library(FSelector)
library(gbm)
sampleA <- bunny_dat[sample(nrow(bunny_dat), nrow(bunny_dat) / 2, replace = F), c("x",
"y",
"input_noise_1",
"input_noise_2",
"input_noise_3",
"input_noise_4",
"input_noise_5",
"input_noise_6",
"input_noise_7",
"input_noise_8",
"input_noise_9",
"input_noise_10",
"z")]
sampleB <- bunny_dat[!row.names(bunny_dat) %in% rownames(sampleA), c("x",
"y",
"input_noise_1",
"input_noise_2",
"input_noise_3",
"input_noise_4",
"input_noise_5",
"input_noise_6",
"input_noise_7",
"input_noise_8",
"input_noise_9",
"input_noise_10",
"z")]
gbm_fit <- function(subset){
dat <- sampleA[, c(subset, "z")]
gbm_fit <- gbm(formula = z ~.,
distribution = "gaussian",
data = dat,
n.trees = 50,
interaction.depth = 10,
n.minobsinnode = 100,
shrinkage = 0.1,
bag.fraction = 0.9,
train.fraction = 1,
n.cores = 7)
gbm_predict <- predict(gbm_fit,
newdata = sampleB,
n.trees = 50)
r_sq_validate <- 1 - sum((sampleB$z - gbm_predict) ^ 2) / sum((sampleB$z - mean(sampleB$z)) ^ 2)
print(subset)
print(r_sq_validate)
return(r_sq_validate)
}
subset <- backward.search(attributes = names(sampleA)[1:(ncol(sampleA) - 1)], eval.fun = gbm_fit)
subset <- forward.search(attributes = names(sampleA)[1:(ncol(sampleA) - 1)], eval.fun = gbm_fit)
Результат при жадном включении предикторов:
> subset
<b>[1] "x" "y"</b>
> r_sq_validate
<b>[1] 0.2363794</b>
Попали в точку!
Результат при жадном исключении предикторов:
> subset
<b> [1] "x" "y" "input_noise_1" "input_noise_2" "input_noise_3" "input_noise_4" "input_noise_5" "input_noise_6" "input_noise_7"
[10] "input_noise_9" "input_noise_10"</b>
> r_sq_validate
<b>[1] 0.2266737</b>
Тут все хуже. Включение шумовых предикторов в модель не сильно ухудшило качество предсказания на валидации. И этому есть объяснение: случайные леса решений имеют встроенный регуляризатор и могут сами игнорировать неинформативные входы в процессе обучения.
На этом мы завершим раздел экспериментов по ОИП на стандартных методах. И в следующем разделе я обосную и покажу практическое применение, на мой взгляд, статистически достоверного и делающего свою работу неплохо, метода на основе информационных метрик.
3) Использование теории информации для построения фитнесс-функции ОИП.
Ключевой вопрос этого раздела — как описать понятие зависимости и сформулировать его в информационно-теоретическом смысле.

Нужно начать с понятия информационной энтропии. Энтропия (шенноновская) — это синоним неопределенности. Чем более мы неуверенны относительно значения случайной величины, тем больше энтропии (еще один синоним — информации) несет реализация данной величины. Если рассмотреть пример с подбрасыванием монеты, то наибольшая энтропия будет у симметричной монеты из всех любых других вариантов монет, потому что мы имеем наибольшую неопределенность в следующем исходе подбрасывания.
Формула для шенноновской энтропии:
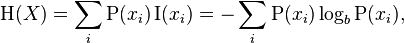
Что же такое зависимость?
Предположим, что мы подбрасываем монету несколько раз. Можем ли мы сказать, что наша неуверенность относительного следующего исхода броска уменьшилась после того, как мы увидели результат предыдущего броска?
Предположим, у нас есть монета, которая приземляется орлом с вероятностью 2/3 после выпадения решки и наоборот — после выпадения орла она приземляется на решку с вероятностью 2/3. При этом безусловная частота выпадений орла и решки остается 50/50.
Для такой монеты после выпадения орла частота выпадения решки уже не равна 1/2, также и наоборот. Так, наша неуверенность относительно следующего исхода броска уменьшилась (мы уже не ожидаем 50/50).
Для понимания феномена зависимости вспомним, что теория вероятностей определяет независимость так:
p(x,y) == p(x) * p(y)
таким образом, вероятность совместной реализации событий равна произведению вероятностей их собственных реализаций.
Если это наблюдается, события независимы в математическом смысле. Если же
p(x,y) != p(x) * p(y)
тогда события математически не независимы.
Этот же принцип лежит в основе формулы для измерения зависимости между двумя (и более) случайными величинами в теории информации.
Подчеркнем, что здесь зависимость понимается в вероятностном смысле. Анализ причинности требует более комплексного обзора, включающего как анализ ложных корреляций и избыточности (через применение взаимной информации), так и привлечение экспертного знания об изучаемом объекте.
Взаимная информация
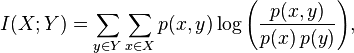
Также можно вывести взаимную информацию через энтропии:
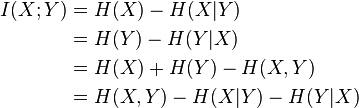
Если сказать простыми словами, взаимная информация это количество энтропии (неопределенности), которое уходит из системы, при наличии предиктивной переменной (или нескольких переменных). Например, энтропия случайной величины равна 3 битам. Взаимная информация равна 2 битам. Значит, на 2/3 неопределенность относительно реализации случайной величины компенсируется наличием предиктора.
Взаимная информация обладает следующими свойствами:
- симметричность
- может быть определена для дискретных и непрерывных переменных
- обращается в ноль, если X и Y независимы
- нормализованная мера взаимной информации принимает значение 1, если две переменные полностью детерминируют друг друга
Взаимная информация удовлетворяет некоторым требованиям, предъявляемым к идеальной мере зависимости, сформулированным в:
Granger, C, E. Maasoumi e J. Racine, ‘A Dependence Metric for Possibly Nonlinear Processes’, Journal of Time Series Analysis 25, 2004, 649-669.
Есть одно свойство взаимной информации (ВИ), которые полезно знать, применяя данную меру:
- ВИ может достигать своего максимума, равного меньшему из значений энтропии для входа и выхода (предиктора и зависимой переменной).
Это означает, что если у нас входная переменная обладает энтропией 10 бит, а выходная — 3 бита, то максимум информации, которая входная переменная может передавать выходной равна 3 битам. Это максимум ВИ, которой может быть в такой системе.
Другой вариант — входная переменная обладает энтропией 3 бита, а выход — 10 бит. Максимум информации, которую вход может нести на выход — 3 бита, и это возможный максимум ВИ.
Если значение ВИ поделить на энтропию зависимой переменной, получится величина в диапазоне [0, 1], что, по аналогии с коэффициентом корреляции, говорит о том, как, без учета масштаба значений, входная переменная детерминирует зависимую.
Есть ряд аргументов за то, что использование ВИ является предпочтительным, хотя и сопряжено с рядом компромисов:
- Метод позволяет находить зависимости произвольного вида (линейные и нелинейные) в пространстве произвольной размерности;
- Метод исключит все входные переменные, если их суммарная или индивидуальная информативность ниже статистически значимой;
- Слабой стороной метода является тот факт, что слабые зависимости — которые едва превышают уровень статистического шума — будут скрыты от глаз исследователя после применения численно расчитанного квантиля метрики ВИ;
- С небольшим количеством значимых дискретных входных переменных исследователь в состоянии построить человеко-читаемый набор правил, позволяющих дать интерпретацию найденным зависимостям;
- Нет неоходимости составлять рандомизированные комитеты моделей (по аналогии с random forest и busting machines), так как метод в себе пробует множество возможных уровней «глубины дерева» для всех отобранных предикторов и возвращает наиболее значимую, в статистическом смысле, комбинацию информативных признаков;
- Метод очень дорогой, особенно по сравнению с другими методами, сочатающими жадный градиентный спуск и более простую фитнесс-функцию, не требующую симуляционных поправок;
- Также стоит отметить, что применение метода имитации отжига для поиска поднаборов предикторов, как и другие методы стохастического спуска, не гарантирует нахождение глобального минимума за разумное число итераций.
Избыточность набора данных.
В наборе входных переменных может существовать взаимозависимость, иначе говоря, зависимость одного или нескольких входных переменных от набора других входных переменных. Если избыточность не устранить, в модель попадут лишние входы, которые не несут существенной информации, что может приводить к переобучению и эффекту коллинеарности.
Для квантования и измерения избыточности есть специальная метрика из теории информации — Мультиинформация (Multiinformation) или Тотальная корреляция (Total Correlation).
Источник:
Ее формула:
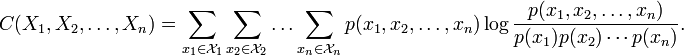
Данная мера была впервые представлена в:
Watanabe S (1960). Information theoretical analysis of multivariate correlation, IBM Journal of Research and Development 4, 66–82
Мультиинформация (МИ) принимает положительное значение в случае, когда вероятность совместной реализации всех входящих переменных начинает отличаться от произведения их маргинальных вероятностей. Интуиция этой метрики в том, что если любой поднабор переменных (от 1 до n) зависит от любого другого поднабора переменных (от 1 до m), то формула дает нам одним числом представление о силе этой зависимости. Максимум мультиинформации соответствует ситуации, когда какой-либо поднабор из переменных полностью детерминирован другим поднабором.
Данная метрика полезна, когда нужно оценить избыточность входных данных в найденном поднаборе.
Если говорить о мерах из теории информации в целом, часто задают вопрос, почему Шеннон определил энтропию именно через логарифм вероятности. Он сам отвечает на вопрос следующим образом:
- 1) Она удобна практически. Параметры, важные в инженерных приложениях — такие, как время, пропускная способность, число переключателей и так далее — обычно меняются линейно при логарифмическом изменении числа возможных вариантов. К примеру, добавление одного переключателя удваивает число возможных состояний их группы, увеличивая на единицу его логарифм по основанию 2. Увеличение в два раза времени приводит к квадратичному росту числа сообщений, или удвоению их логарифма, и так далее.
- 2) Она близка к нашему интуитивному представлению о такой мере. Это тесно связано с предыдущим пунктом, так как мы интуитивно измеряем величины, линейно сравнивая их со стандартами. Так, нам кажется, что на двух перфокартах можно разместить в два раза больше информации, а по двум одинаковым каналам — передать её в два раза больше.
- 3) Она удобна математически. Многие предельные переходы просты в логарифмах, в то время как в терминах числа вариантов они достаточно нетривиальны.
Для получения более полного предствления о мерах из теории информации я приглашаю читателя обратиться, например, к работам:
Акива Моисеевич Яглом, Исаак Моисеевич Яглом. Вероятность и информация. Издание третье, переработанное и дополненное. М., Наука, 1973 — 512 с.
Колмогоров А.Н. — «Теория информации и теория алгоритмов».
Поправка значения МИ и ВИ, полученных на ограниченной выборке.
Несмотря на доступность пакетов и функций, которые без особых усилий посчитают вам любую метрику из теории информации, важно понимать, что эти метрики являются наивным приближением истинных значений в силу того, что получены они на эмпирическом распределении и выборке ограниченного размера.
Интуиция такого рода поправок состоит в том, что найденные зависимости на нашей выборке размером n могут скорректироваться при увеличении выборки до N.
Рост размера выборки ведет к уменьшению зависимости. Приведены данные, где априори не заложено никаких зависимостей.
Численная оценка наивной взаимной информации на случайной выборке из 100 наблюдений.
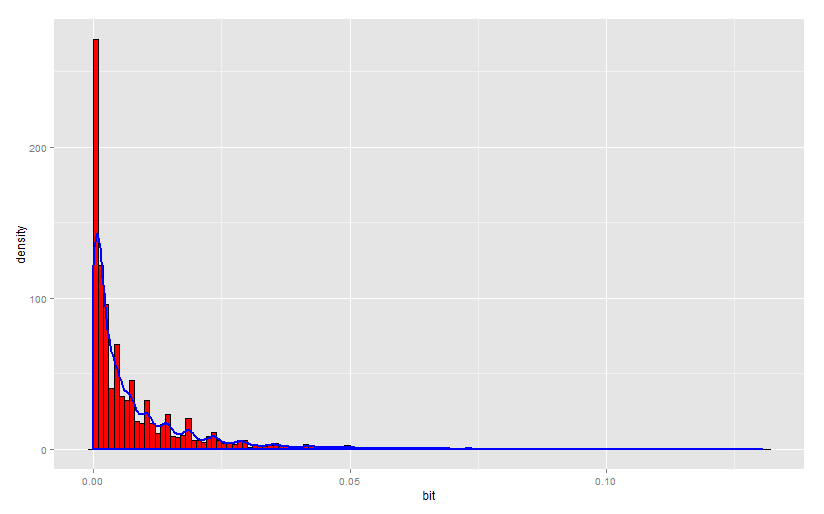
Численная оценка наивной взаимной информации на случайной выборке из 1000 наблюдений.
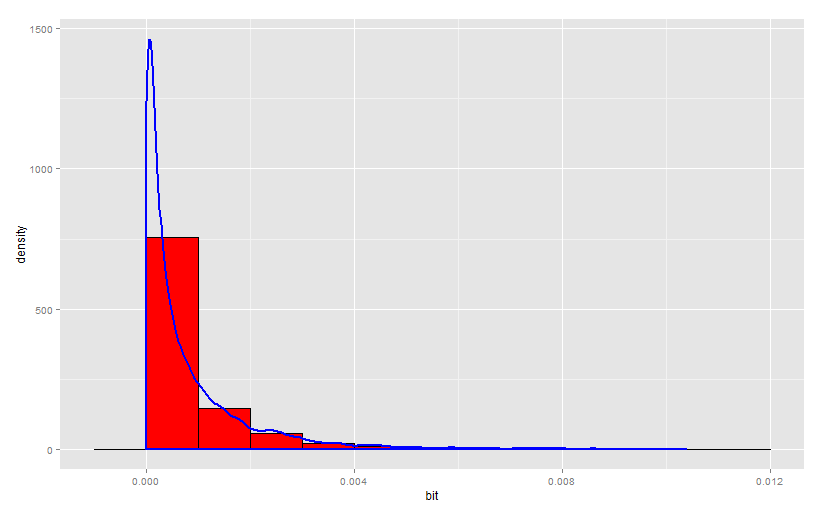
Рост объема выборки это главный фактор, влияющий на шумовое количество ВИ, которое стремится к нулю при предельно большой выборке.
В идеале, мы хотели бы иметь меру зависимости, которая справедлива для выборки бесконечного размера. Это так называемая ассимптотическая величина, оценить которую брались ряд ученых коллективов с самого зарождения теории информации. См.:
Есть ряд известных названий поправок значений ВИ и МИ, а также энтропии, с учетом ограниченной выборки. Их полезность можно оценить только путем проведения экспериментов с данными. Мы пытались оценить ассимптотическое значение взаимной информации для небольшой выборки, не содержащей никаких зависимостей априори (данные были синтетическими). При этом ассимптотические поправки устроены так, что даже на таких шумовых данных они начинают показывать наличие зависимостей.
Чтобы преодолеть эту особенность информационных мер есть путь гораздо более долгий, но показывающий устойчивые и обоснованные результаты.
Мы используем случайное перемешивание значений выходной переменной при зафиксированной структуре входных данных. Таким образом мы полностью разрушаем эмпирические зависимости и на множестве итераций этого процесса фиксируем полученные значения ВИ. В результаты есть распределение значений ВИ на данных, в которых отсутствуют зависимости, но сохранены распределения входов и выхода. Мы оцениваем заданный заранее квантиль полученного распределения.
Такую же операцию можно произвести для коррекции значения мультиинформации (меры избыточности в данных), но на этот раз случайное перемешивание затрагивает все входящие переменные и разрушаются связи между любыми поднаборами переменных при сохранении собственных распределений переменных.
Однако один момент остается нерешенным. Это ассимптотическая мера энтропии переменных. Не представляется возможным, без введения дополнительных предположений, скорректировать маргинальное распределение вероятностей, данное эмпирически. Иными словами, если монета при 1 000 бросках выпала орлом в 51% случаев, то без знания физических свойств объекта сложно что-то сказать о доверительном интервале вероятности на пространстве исходов процесса. Поэтому в нашем подходе энтропия остается оцененной наивно. Но поработать над этим вопросом еще можно в будущем.
Блок-схема работы алгоритма на основе скорректированной взаимной информации и стохастического поиска поднабора предикторов.
- а) Привести набор данных к категориальному виду одним из известных способов.
- б) Оценить такие параметры набора данных, как количество строк, предикторов, среднее количество уровней предикторов (если они имеют разное количество уровней) и на основе этих данных посчитать «оптимальное количество» предикторов в финальном поднаборе.
- в) Инициализировать вектор типа numeric длиной в количество входных переменных с помощью случайных чисел, равномерно распределенных в диапазоне [0, 1] и задать нижнюю (0) и верхнуюю (1) границу для значений вектора — это аргументы функции SA.
- г) Инициализировать функции оценки квантиля мультиинформации, квантиля взаимной информации, фитнесс-функцию, объединяющую все расчеты.
- д) Задать количество симуляций Монте-Карло для оценки квантилей МИ и ВИ; задать квантили (например, 0.9) для шумовых значений МИ и ВИ.
- е) Задать время или количество итераций работы алгоритма. Чем больше, тем лучше.
- ж) Запустить алгоритм, дождаться результатов.
Пункт «б» требует пояснения. Оптимальное количество переменных — это условная величина, которая определятся по формуле:
optim_var_num < — log(x = sample_size / 100, base = round(mean_levels, 0))
Интуиция в том, что, при допущении о независимости входных переменных, среднее количество уровней переменной нужно возвести в искомую степень с тем, чтобы получить общее количество уникальных взаимодействующих уровней такое, чтобы на каждом из них в среднем концентрировалось не менее n наблюдей, где n принято в эксперименте за 100.
Мы не можем включить слишком много входных переменных с большим количеством уровней, так как консервативная оценка частоты наблюдений по входным уровням получится слишком маленькая для того, чтобы дать статистическое заключение о зависимости выходной переменной от набора входных.
При этом, устанавливая порог, выше которого значения вектора длиной в количество входных переменных будут преобразовываться в единицу (флаг включения индекса переменной), мы делаем вероятностный расчет:
threshold < — 1 — optim_var_num / predictor_number
Суть его сводится к тому, что мы задаем максимальное значение вероятности для отбора вычисленного оптимального количества входов. И проверяется эта логика применением биномиального распределения.
Например, возьмем наши данные: половину всего набора, которая используется для обучения.
У нас 17 973 строки, 12 предикторов, в каждом по 5 уровней. В результате применения вышеописанных формул мы получаем, что оптимальное количество предикторов равно 3,226.
Применяя формулу порога для включения предиктора в набор, получаем 0,731.
Какое наиболее вероятное количество отобранных переменных будет получено на биномиальном распределении?
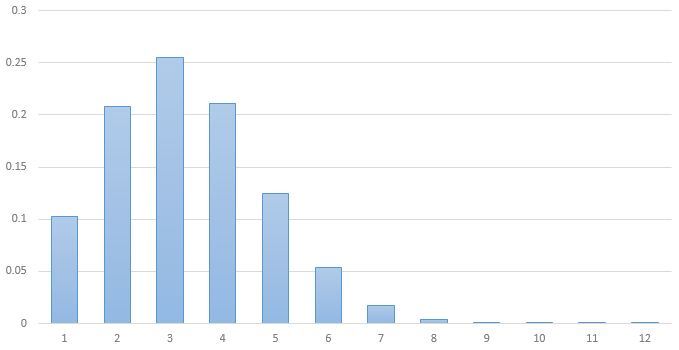
Наиболее вероятным является 3 наблюдения. Если быть точным, то 5 ^ 3,226 даст нам 178 уровней, на которых в среднем разместится по 100 наблюдений.
Проведем эксперимент с использованием приведенных рассуждений.
Эксперимент №8 оценка важности предикторов, используя стохастический (нежадный) поиск с оценкой важности при помощи взаимной информации (это нежадный поиск в пространстве входов, фитнесс-функция — скорректированная на шум и избыточность взаимная информация).
Эксперимент будет запущен при симуляции 0,9 квантиля ВИ (на шуме) при 10 итерциях Монте-Карло, и квантиля 1 при 1 итерации для корректировки МИ (на шуме). Время пока поставим 10 минут.
############## simlated annelaing search with mutual information fitness function
library(infotheo) # measured in nats, converted to bits
library(scales)
library(GenSA)
sampleA <- bunny_dat[sample(nrow(bunny_dat), nrow(bunny_dat) / 2, replace = F), c("x",
"y",
"input_noise_1",
"input_noise_2",
"input_noise_3",
"input_noise_4",
"input_noise_5",
"input_noise_6",
"input_noise_7",
"input_noise_8",
"input_noise_9",
"input_noise_10",
"z")]
sampleB <- bunny_dat[!row.names(bunny_dat) %in% rownames(sampleA), c("x",
"y",
"input_noise_1",
"input_noise_2",
"input_noise_3",
"input_noise_4",
"input_noise_5",
"input_noise_6",
"input_noise_7",
"input_noise_8",
"input_noise_9",
"input_noise_10",
"z")]
# discretize all variables
dat <- sampleA
disc_levels <- 5
for (i in 1:13){
naming <- paste(names(dat[i]), 'discrete', sep = "_")
dat[, eval(naming)] <- discretize(dat[, eval(names(dat[i]))], disc = "equalfreq", nbins = disc_levels)[,1]
}
sampleA <- dat[, 14:26]
#calculate parameters
predictor_number <- dim(sampleA)[2] - 1
sample_size <- dim(sampleA)[1]
par_v <- runif(predictor_number, min = 0, max = 1)
par_low <- rep(0, times = predictor_number)
par_upp <- rep(1, times = predictor_number)
#load functions to memory
shuffle_f_inp <- function(x = data.frame(), iterations_inp, quantile_val_inp){
mutins <- c(1:iterations_inp)
for (count in 1:iterations_inp){
xx <- data.frame(1:dim(x)[1])
for (count1 in 1:(dim(x)[2] - 1)){
y <- as.data.frame(x[, count1])
y$count <- sample(1 : dim(x)[1], dim(x)[1], replace = F)
y <- y[order(y$count), ]
xx <- cbind(xx, y[, 1])
}
mutins[count] <- multiinformation(xx[, 2:dim(xx)[2]])
}
quantile(mutins, probs = quantile_val_inp)
}
shuffle_f <- function(x = data.frame(), iterations, quantile_val){
height <- dim(x)[1]
mutins <- c(1:iterations)
for (count in 1:iterations){
x$count <- sample(1 : height, height, replace = F)
y <- as.data.frame(c(x[dim(x)[2] - 1], x[dim(x)[2]]))
y <- y[order(y$count), ]
x[dim(x)[2]] <- NULL
x[dim(x)[2]] <- NULL
x$dep <- y[, 1]
rm(y)
receiver_entropy <- entropy(x[, dim(x)[2]])
received_inf <- mutinformation(x[, 1 : dim(x)[2] - 1], x[, dim(x)[2]])
corr_ff <- received_inf / receiver_entropy
mutins[count] <- corr_ff
}
quantile(mutins, probs = quantile_val)
}
############### the fitness function
fitness_f <- function(par){
indexes <- c(1:predictor_number)
for (i in 1:predictor_number){
if (par[i] >= threshold) {
indexes[i] <- i
} else {
indexes[i] <- 0
}
}
local_predictor_number <- 0
for (i in 1:predictor_number){
if (indexes[i] > 0) {
local_predictor_number <- local_predictor_number + 1
}
}
if (local_predictor_number > 1) {
sampleAf <- as.data.frame(sampleA[, c(indexes[], dim(sampleA)[2])])
pred_entrs <- c(1:local_predictor_number)
for (count in 1:local_predictor_number){
pred_entrs[count] <- entropy(sampleAf[count])
}
max_pred_ent <- sum(pred_entrs) - max(pred_entrs)
pred_multiinf <- multiinformation(sampleAf[, 1:dim(sampleAf)[2] - 1])
pred_multiinf <- pred_multiinf - shuffle_f_inp(sampleAf, iterations_inp, quantile_val_inp)
if (pred_multiinf < 0){
pred_multiinf <- 0
}
pred_mult_perc <- pred_multiinf / max_pred_ent
inf_corr_val <- shuffle_f(sampleAf, iterations, quantile_val)
receiver_entropy <- entropy(sampleAf[, dim(sampleAf)[2]])
received_inf <- mutinformation(sampleAf[, 1:local_predictor_number], sampleAf[, dim(sampleAf)[2]])
if (inf_corr_val - (received_inf / receiver_entropy) < 0){
fact_ff <- (inf_corr_val - (received_inf / receiver_entropy)) * (1 - pred_mult_perc)
} else {
fact_ff <- inf_corr_val - (received_inf / receiver_entropy)
}
} else if (local_predictor_number == 1) {
sampleAf<- as.data.frame(sampleA[, c(indexes[], dim(sampleA)[2])])
inf_corr_val <- shuffle_f(sampleAf, iterations, quantile_val)
receiver_entropy <- entropy(sampleAf[, dim(sampleAf)[2]])
received_inf <- mutinformation(sampleAf[, 1:local_predictor_number], sampleAf[, dim(sampleAf)[2]])
fact_ff <- inf_corr_val - (received_inf / receiver_entropy)
} else {
fact_ff <- 0
}
return(fact_ff)
}
########## estimating threshold for variable inclusion
iterations = 10
quantile_val = 0.9
iterations_inp = 1
quantile_val_inp = 1
levels_arr <- numeric()
for (i in 1:predictor_number){
levels_arr[i] <- length(unique(sampleA[, i]))
}
mean_levels <- mean(levels_arr)
optim_var_num <- log(x = sample_size / 100, base = round(mean_levels, 0))
if (optim_var_num / predictor_number < 1){
threshold <- 1 - optim_var_num / predictor_number
} else {
threshold <- 0.5
}
#run feature selection
start <- Sys.time()
sao <- GenSA(par = par_v, fn = fitness_f, lower = par_low, upper = par_upp
, control = list(
#maxit = 10
max.time = 300
, smooth = F
, simple.function = F))
trace_ff <- data.frame(sao$trace)$function.value
plot(trace_ff, type = "l")
percent(- sao$value)
final_vector <- c((sao$par >= threshold), T)
names(sampleA)[final_vector]
final_sample <- as.data.frame(sampleA[, final_vector])
Sys.time() - start
Результат:
> percent(- sao$value)
<b>[1] "18.1%"</b>
> final_vector <- c((sao$par >= threshold), T)
> names(sampleA)[final_vector]
<b>[1] "x_discrete" "y_discrete" "input_noise_2_discrete" "z_discrete" </b>
> final_sample <- as.data.frame(sampleA[, final_vector])
>
> Sys.time() - start
Time difference of 10.00453 mins
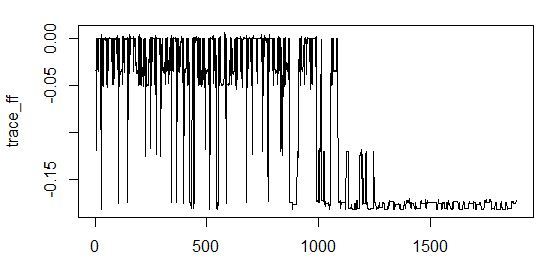
Почти получилось. Однако сходимости за это время алгоритм не показывает. Много данных — требуется больше времени.
Попробуем запустить на 20 минут, и при этом уменьшим количество итераций Монте-Карло до 1 для ускорения обсчета.
Результат:
> percent(- sao$value)
<b><b>[1] "18.2%"</b></b>
> final_vector <- c((sao$par >= threshold), T)
> names(sampleA)[final_vector]
<b><b>[1] "x_discrete" "y_discrete" "input_noise_1_discrete" </b>"z_discrete" </b>
> final_sample <- as.data.frame(sampleA[, final_vector])
>
> Sys.time() - start
Time difference of 20.00585 mins
Также нет идеального решения — к хорошим входам добавлен один шумовой предиктор.
При этом полученная взаимная информация на 18% компенсирует энтропию зависимой переменной. Неплохое значение.
Сходимость неплохая (график почти полностью ушел на уровень хороших энергетических значений):
Minimum-redundancy-maximum-relevance (mRMR)
Идея максимизиации релевантности набора фичей и минимизации их избыточности не нова. Метод с соответствующим названием был представлен в:
Несмотря на рациональность метода и хороший повод для его внедрения в практику, у нас (а также у статистического сообщества) есть ряд методологических претензий. Источник.
Реализация метода автором подразумевает замер релевантности как (а) усреднение взаимной информации между каждым из отобранных предикторов и выходом, а замер избыточности как (б) усреднение взаимной информации между всеми входящими в поднабор предикторами.
По пункту (а) можно сделать законное замечание о том, что вся информация, переданная от предикторов на выход, не может быть корректно оценена через простое среднее значение. Остаются незамеченными те зависимости, которые формируются на взаимодействии предикторов и входа.
По пункту (б) также имеет силу замечание о том, что мера взаимосвязи набора предикторов не может быть корректно выведена взятием среднего значения. Как минимум, останутся без внимания зависимости поднаборов от поднаборов (в поднаборе).
Как правильно отмечается в статье на Википедии, эффективность данного алгоритма в ряде случаев под большим вопросом, к тому же легко понять, что оптимальной ситуацией, где алгоритм работает хорошо, является отсутствие взаимодействий и полная (попарная и погрупная) независимость в наборе предикторов, что почти никогда не выполняется. Так же как в случае требований к данным линейной регрессии, mRMR предъявляет солидный набор допущений, без которых результаты его работы будут искажены.
Пункт (в) критики данного подхода заключается в том, что не понятным остается способ коррекции наивной оценки мер зависимости в условиях выборки ограниченного размера — так называемая limited sampling bias.
В противовес приведенным слабым местам в mRMR мы перевели идею максимизации релевантности и минимизации избыточности в плоскость корректной практической реализации.
Подведем итог наших экспериментов и сведем результаты в одну таблицу.
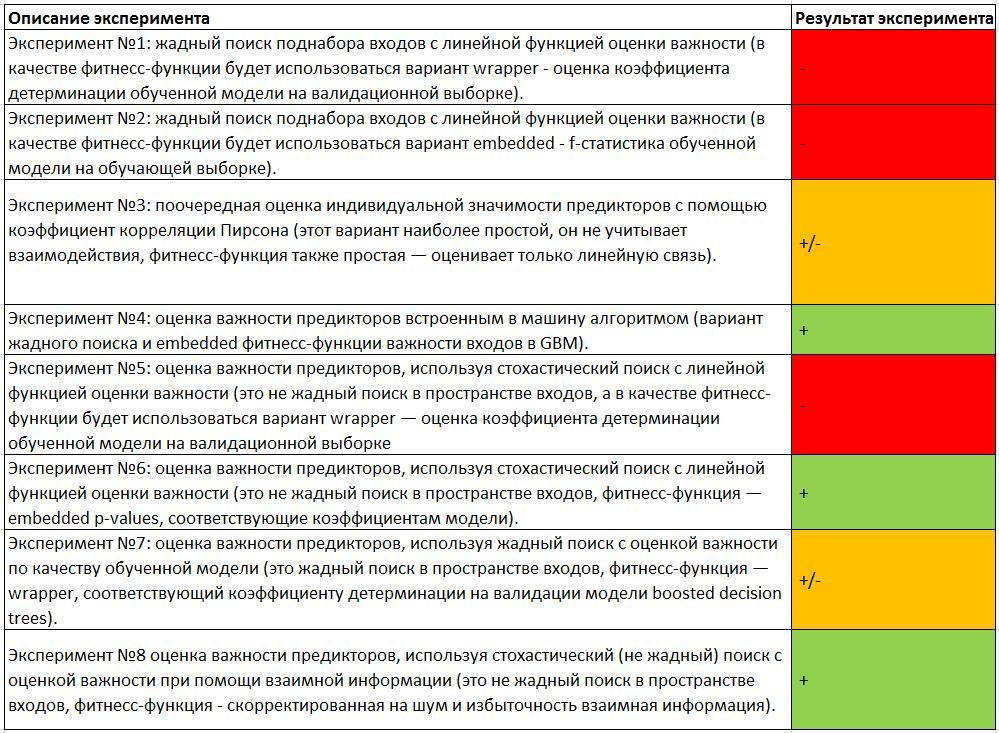
Если подвести некие обобщенные итоги, то у нас получились хорошие результаты, применяя важность предикторов в модели GBM, а также при минимизации p-values в линейной модели.
Применение нежадного поиска совместно с метрикой взаимной информации дало почти идеальный результат, включающий один искусственно введенный шумовой предиктор. Однако расследование показало, что включение этого предиктора действительно максимизирует метрику, несмотря на то, что результат без данного предиктора почти такой же. Получается, что некоторую дополнительную информацию о выходе комбинация X-Y-Noise1 действительно несет. Нам нравится данный алгоритм именно тем, что он позволяет репортовать о важности отобранных входных признаков на заранее заданном уровне доверии (через оценку квантиля), что соответствует духу работы специалистов по статистике в Align Technology. Этот аспект вносит гораздо больше прозрачности в результаты, в отличии от, например, коэффициентов относительной важности в Gradient Boosted Trees (Источник.).
Конечно, мы также можем расчитать статистическую значимость и для других методов, например, для коэффициентов линейной модели или для коэффициентов корреляции. Но мы обращаем внимание читателя на то, что, в отличие от упомянутых мер линейной зависимости, взаимная информация охватывает произвольные виды зависимости, чем и является более привлекательной в своей универсальности.
Применение коэффициента корреляции дало смешанный результат, где сложно было решить, включать ли предиктор или нет. Нужны дополнительные статистические тесты на значимость корреляции. При этом на других наборах, где может вообще отсутствовать линейная связь, данный метод не даст хорошего результата.
На этом я завершаю статью. Не все методы были опробованы, не все тонкости раскрыты, но общее представление об экспериментах с отбором информативных признаков, я надеюсь, у вас появилось. Если у вас будут вопросы и обсуждение, я всегда постараюсь ответить в комментариях.
Код экспериментов в одном файле на github: Git
Использованные источники информации:
- Greedy Function Approximation: A Gradient Boosting Machine by J. Friedman
- Отбор фичей на Википедии
- Акива Моисеевич Яглом, Исаак Моисеевич Яглом. Вероятность и информация. Издание третье, переработанное и дополненное. М., Наука, 1973 — 512 с.
- Колмогоров А.Н. — «Теория информации и теория алгоритмов».
- Analytical estimates of limited sampling biases in different information measures by S. Panzeri at.al.
- Estimation of Entropy and Mutual Information by L. Paninski
- Entropy-Based Independence Test by A. Dionísio at.al.
- Теория информации в задаче проверки гипотезы о независимости значений, принимаемых случайной переменной, на примере индекса DJI, А. Бурнаков
- Measuring dependence powerfully and equitably by Y. Reshef et.al.
- «Feature selection based on mutual information: criteria of max-dependency, max-relevance, and min-redundancy,» Hanchuan Peng, Fuhui Long, and Chris Ding IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 27, No. 8, pp.1226-1238, 2005
- Watanabe S (1960). Information theoretical analysis of multivariate correlation, IBM Journal of Research and Development 4, 66–82
- Gradient boosting machines, a tutorial.
Автор: Align Technology, R&D





