Недавно узнал о том, что фирма STMicroelectronics анонсировала трехосевой гироскоп A3G4250D, удовлетворяющий жесткому стандарту для автомобильного применения (AEC-Q100). Обещана стоимость $6 при заказах от 1000 шт. Класс цены понятен. Захотелось сравнить паспортные характеристики этого датчика с маститыми моделями от Analog Devices Inc. и других производителей. Пока разбирался с даташитами выяснил, что набор паспортных характеристик ADI и STM, к примеру, неодинаковый. Попутно решил выяснить по каким все-таки попугаям стоит сравнивать датчики, т.е. что является наиболее серьезной проблемой микромеханики. В итоге набрался материал для поста, а может и двух. В данном будет вводная. Сравнение a la "[30 коп. пучок] Vs. [Чугунный мост]" к сожалению не уместилось.
Введение
О принципах работы разных классов микромеханических гироскопов и акселерометров можно написать ни одну статью. Существует несколько обособленных видов/классов приборов. Если не вдаваться в подробности, грубо можно сказать следующим образом.
Чувствительным элементом (ЧЭ) микромеханического гироскопа является инерционная масса, закрепленная внутри корпуса на пружинах (упругих консолях полупроводника и пр.). Эта чувствительная масса приводится в колебательное движение по одной из осей датчика. Эта ось является осью возбуждения (входной осью). По этой оси задается рабочий режим. Измерения же производятся по перпендикулярной к ней оси (выходной). Принцип действия заключается в том, что при вращении корпуса вокруг его измерительной оси ( ее еще называют осью чувствительности) чувствительный элемент помимо колебаний вдоль входной оси начинает колебаться еще и вдоль третьей, выходной. Если кто знает, что такое Фигуры Лиссажу, тот легко поймет, что ЧЭ начинает описывать в пространстве окружность (или эллипс).
Так упрощенно работает одноосевой датчик. У двух и трехосевых датчиков комплекс из ЧЭ и измерительной системы как бы обрамляется еще одной системой подвеса/измерителей. Т.е. одна сборка ЧЭ/Подвес/Измерители (пусть это будет сборка для оси Х) сама является колеблющимся ЧЭ для другой сборки (напр., по ОY), которая входит в сборку для измерения по OZ. Возможна, наверняка, и раздельная система.
Специалист по микромеханике в тексте выше сможет найти достаточно некорректностей. Написано грубо и для простоты восприятия. И написано это, чтобы плавно перейти к описанию одной из серьезнейших проблем микромеханики, а именно чувствительность к линейным ускорениям.
В теории колеблющийся ЧЭ не должен чувствовать ускорений и не должно у него быть перекрестных связей (в случае двух- или трехосевых датиков) с другими осями чувствительности (ОЧ). Но вследствие неидеальностей создания трехмерной структуры внутри интегральной микросхемы центры масс ЧЭ смещаются, появляются остаточные напряжения в материале, пружины имеют неодинаковые упругости и т.д. В результате ЧЭ для ОХ начинает реагировать на воздействия по OY, линейные ускорения начинают искажать показания гироскопа. Т.е. в измерениях появляется приращение угловой скорости которого на самом деле нет (случайный дрейф).
Сделать производство ЧЭ идеальным невозможно (или не целесообразно), поэтому в конструкции датчиков появляются дополнительные элементы, нужные для уменьшения чувствительности к упомянутым паразитным воздействиям. В первую очередь простотой и даже самим наличием элементов режекции паразитных воздействий как раз и отличаются дешевые (до $10-15) датчики от датчиков среднего ($30-100) и верхнего ($100+) ценовых диапазонов.
В одной из хабрастатей я обсуждал вопрос пренебрежимости реакции недорогих гироскопов на паразитные воздействия (тут например). Понятно, что для статичного квадракоптера незачем изгаляться. Но ведь это лишь демо-устройство будет использоваться в статике. UAV должен перемещаться, причем иметь достойные динамические характеристики. Иначе зачем он сможет быть использованным? Для поглядеть, а что там за забором?
Про реакцию на вибрации, которые имеют высокую интенсивность в квадракоптерах к примеру, особо рассказывать не нужно. Все знают что это такое. Поэтому считаю, что вопрос чувствительности гироскопов к ускорению и вибрациям очень важен для создания подвижного объекта с нормальной динамикой.
Погрешности микромеханических гироскопов
Первое, что бросается в глаза разработчикам в даташитах к датчикам, это так называемая «стабильность нуля». Ведь кажется, что именно этот параметр в конечном итоге определяет чувствительность датчика, т.е. минимальное входное воздействие, которое датчик почувствует. Так из-за низкой стабильности нуля многих моделей ММГ, до сих пор многие считают, что микромеханические гироскопы (ММГ) не чувствуют вращение Земли. Есть модели ММГ имеющие стабильность нуля немногим более 2 °/час (Земля, как известно вращается со скоростью 15 °/час). Но на практике это не означает, что измерить вращение Земли все-таки удастся.
Как бы то ни было, разработчик смотрит на стабильность нуля. Это понятный параметр, показывающий в каких пределах будет колебаться нуль шкалы датчика в лабораторных условиях. Однако это параметр стабильности «сферического коня в вакууме». В реальности заявленной стабильности не будет. Почему? Да потому, что там указана стабильность (вернее нестабильность) обусловленная внутренними источниками погрешностей. В каких условиях датчик будет работать производитель не сможет предугадать, как и вызванные этими условиями девиации.
Есть два подхода борьбы с погрешностями: аппаратный и алгоритмический (читай программный). Второй подход подразумевает добавление в прошивку БЦЭВМ специальных программных модулей для коррекции ошибок, вызванных паразитными процессами. И этот подход не рекомендуется как оптимальный. В первую очередь сам датчик должен гасить шумы. Центральный должен заниматься не вычищением основного мусора, а финишной обработкой и обсчетом высокоуровневых алгоритмов (навигация, стабилизация, автоматизация). Есть разного рода методические погрешности. Они легко описываются некими формулами, вот их легко компенсировать программно.
К чему все это? А к тому, что правильнее выбрать датчики, оптимальные с точки зрения соотношения цены к точностным характеристикам. И тут главными параметрами выбора будет скорее всего чувствительности гироскопа к линейному ускорению (g-чувствительность) и вибрациям (g²-чувствительность). Почему они главные объясняется ниже.
Температурный гистерезис нуля
ММГ имеют погрешности нуля, которые варьируются в зависимости от температуры внутри корпуса. Для проведения термокомпенсации в ММГ встроены температурные датчики. Их точность особого значения не имеет, важна лишь повторяемость показаний. Но с термокомпенсацией есть проблема — гистерезис. Гистерезис в данном случае — это разница между требуемым значением коррекции для конкретной температуры в двух случаях — когда прибор достигает этой температуры охлаждаясь и в случае, когда он нагревается до той же температуры. См. график ниже.
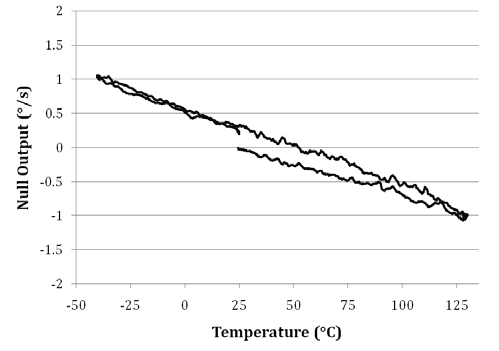
На этом графике показан температурный гистерезис нуля для ММГ ADXRS453 при изменении температуры от +25°С к +130°С, потом к -45°С и обратно к +25°С. Этот гистерезис имеет место не зависимо от того включен датчик во время колебания температуры или нет. К тому же гистерезис зависит от того, насколько широк диапазон изменения температур.
Ситуация сложная? Нет, не очень. В общем случае ММГ не должны использоваться для определения углов ориентации при отсутствии некоторой внешней референсной системы, которая позволяет сбросить накопившуюся погрешность до некоторого низкого уровня. По той же системе можно определить и текущее смещение нуля. Таким образом, температурные смещение нуля и погрешность масштабного коэффициента при нормальном применении достаточно эффективно могут компенсироваться (пусть и с точностью до некоторой малой, ненулевой величины).
Погрешности из-за вибраций
Как было написано выше, сферический ММГ в вакууме измеряет лишь вращение и ничего другого. Однако из-за несимметричности ЧЭ и неидеальности изготовления все ММГ чувствуют ускорения. Под чувствительностью к ускорениям чаще всего понимают чувствительность к линейному ускорению (g-чувствительность) и к линейным вибрациям (g²-чувствительность). На объекты, движущиеся в поле тяготения Земли, в любом случае действует ускорение (кроме случаев свободного падения). Чувствительность к линейным ускорениям часто оказывается главным источником погрешностей.
ММГ в самом низком ценовом диапазоне оптимизированы прежде всего по стоимости, но не по сопротивлению вибрациям. Они имеют относительно простую механическую систему. Она хоть и отличается живучестью (выдерживает гигантские перегрузки в 10'000 g), но не защищена от вибраций. Малая масса чувствительного элемента -> широкая полоса пропускания. В таких гироскопах чувствительность к ускорению (acceleration effect в даташитах) может быть равна 1000 °/час/g (или 0.3 °/сек/g). И это значение вполне себе нормальное для такого класса датчиков. Но это на порядок выше, чем следует ожидать от точных датчиков. От дешевых датчиков не стоит ожидать стабильности нуля в контексте чувствительности к ускорениям. Даже малые вращения в поле тяготения Земли приводят к огромным погрешностям из-за их чрезвычайной чувствительности к ускорению и вибрациям. К слову сказать, «aceleration effect» я не нашел в даташите к A3G4250D от STMicroelectronics. Этот параметр не специфицируется для данного класса датчиков. Он просто подразумевается большим. Ниже представлена сравнительная таблица для некоторых моделей ММГ более высокого класса.

В этой таблице представлены датчики, относящиеся к классу точных. И даже для них оба параметра не всегда указываются производителем.
Часто для компенсации чувствительности к ускорению пользуются коррекцией по показаниям акселерометра. Ниже пример из комментариев к хабрапосту "Использование инерциальной навигационной системы (ИНС) с несколькими датчиками на примере задачи стабилизации высоты квадрокоптера" на тему квадрокоптеров:
Если дрифт постоянный и всегда в одну сторону — это всего лишь говорит о неправильной калибровке 0. В MultiWii 0 гир калибруется при каждом включении, но неидеально (округляется до целого), если ввести хотя бы десятые становится намного лучше. Но в данном применении гироскопа, даже ощутимый дрейф не страшен, так как есть референсная ориентация (компасс и акселерометр) по которой он исправляется.
Но оказывается дрейф из-за чувствительности к ускорениям зависит от частоты с которой это ускорение меняется. Ниже представлены графики зависимости выходного сигнала ММГ CRG20-01 (в штучных поставках в виде demo-board обойдется, если не ошибаюсь, в районе $100-150 с доставкой) от частоты изменения приложенного ускорения.
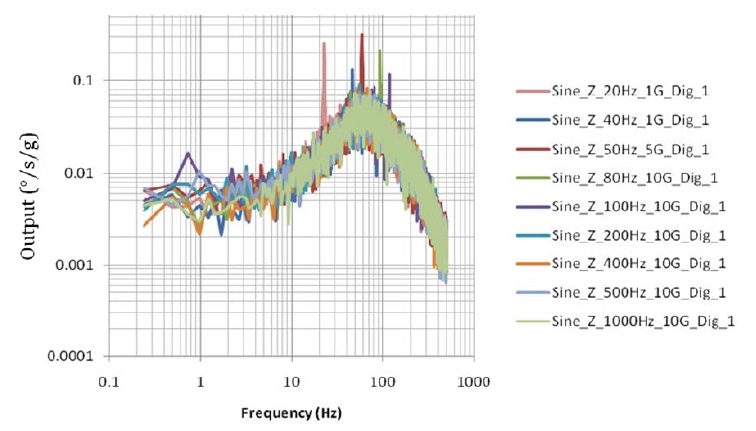
На графике видно, что от амплитуды ускорения погрешность не зависит. А вот от частоты зависимость имеется. И просто так эту погрешность не скомпенсируешь (большая вариация и сложная кривая изменения чувствительности). Скомпенсировать g²-чувствительность, если она постоянна, несложно. Но опять же не все производители в даташитах указывают графики для этого параметра. Разработчику часто приходится самому экспериментально строить эти графики. И часто это производится в полевых условиях на уже запущенных в эксплуатацию приборах.
Еще одна засада с коррекцией по акселерометрам — согласование фаз. В общем случае собственные частоты акселерометра и гироскопа не совпадают, да и частотные характеристики вообще. Поэтому при различных частотах вибраций ММА и ММГ будут выдавать разные смещения по фазе выходного сигнала относительно вибраций на входе. В конечном итоге коррекция по акселерометру может увеличить! погрешность вместо ее гашения. Случится это, если разница между смещениями по фазе ММА и ММГ будет приближаться к значению 3,14 радиан (180 градусов).
В итоге, т.к. чувствительность к вибрациям и ускорениям сильно варьируется даже в рамках одной модели датчика или она слишком велика, производитель ее просто не указывает. Правда нужно заметить, на самом деле достаточно трудно протестировать датчики на чувствительность к вибрациям. Проблемы носят как технический, так и методологический характер.
Для снижения чувствительности к вибрациям можно, конечно крепить датчики через резиновый изолятор. Но сделать так, чтобы этот подвес имел равномерное распределение характеристик для широкого диапазона частот, да еще и не менял их при старении очень сложно.
Ниже представлено сравнение погрешностей из-за чувствительности к ускорению и вибрациям, когда не используется g-компенсация (в гр/сек).

А в следующей таблице представлены погрешности, которые остаются даже после введения g-компенсации (в гр/сек).

Как видим даже при введении g-компенсации погрешность от чувствительности к ускорениям все равно может быть больше погрешности от температурной нестабильности нуля (см. график гистерезиса выше).
Выводы
Написанное выше говорит о том, что не всегда самый очевидный параметр точности является и главным критерием выбора датчиков. «Под свечей всегда темно», — говорит народная мудрость. То, что недостаточно четко описано в даташите или вообще не указано может сыграть решающую роль в успешности проекта. Можно заострить внимание на стабильности нуля и дисперсии шумов, а ведь их можно победить несложными алгоритмами (усреднять во времени или с использованием избыточных измерительных блоков). Зато погрешность от вибраций, как мы увидели выше на примере CRG20-01, может оказаться трудным описать в алгоритме. Долгое время стабильность нуля является золотым стандартом выбора ММГ. Однако на практике большее влияние на точность может оказать чувствительность к ускорениям и вибрациям.
Заключение
Хотел сделать пост, содержащий две части — 1) Обоснование выбора критерия сравнения и 2) Сравнение по ТТХ моделей от Analog Devices Inc., Silicon Sensing, Sensonor и STMicroelectronics. Однако и так получилось «многабукв». Если будет интересно, постараюсь в скором времени сравнить по даташитам датчики упомянутых фирм с разъяснением о физическом смысле основных характеристик.
UPD: поправлены некоторые опечатки и грамматические ошибки.
Автор: HomoLuden






