Создание крюка-кошки в Unity. Часть 2

Примечание: этот туториал предназначен для продвинутых и опытных пользователей, и в нём не рассматриваются такие темы, как добавление компонентов, создание новых скриптов GameObject и синтаксис C#. Если вам нужно повысить навыки владения Unity, то изучите наши туториалы Getting Started with Unity и Introduction to Unity Scripting.

В первой части туториала мы научились создавать крюк-кошку с механикой оборачивания верёвки вокруг препятствий. Однако мы хотим большего: верёвка может оборачиваться вокруг объектов на уровне, но не отцепляется, когда вы возвращаетесь обратно.

Приступаем к работе

Откройте готовый проект из первой части в Unity или скачайте заготовку проекта для этой части туториала, после чего откройте 2DGrapplingHook-Part2-Starter. Как и в первой части, мы будем использовать Unity версии 2017.1 или выше.

Откройте в редакторе сцену Game из папки проекта Scenes.

Запустите сцену Game и попробуйте прицепиться крюком-кошкой к камням над персонажем, а затем покачаться, чтобы верёвка обернулась вокруг пары рёбер камня.

При возврате назад вы заметите, что точки камня, через которые верёвка раньше оборачивалась, не отцепляются снова.

Подумаем о точке, в которой верёвка должна разворачиваться. Чтобы упростить задачу, лучше использовать случай, когда верёвка оборачивается вокруг рёбер.

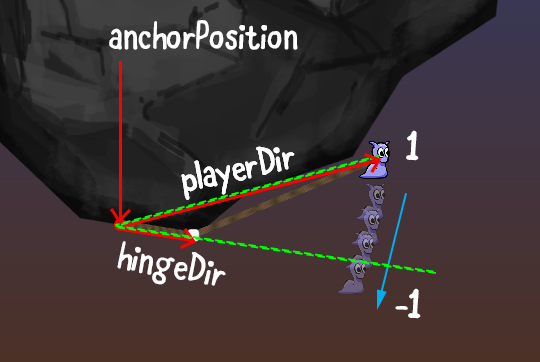
Если слизняк, прицепившись к камню над головой, качается вправо, то верёвка загнётся после порога, в которой она пересекает точку угла в 180 градусов с ребром, к которому в текущий момент прицеплен слизняк. На рисунке ниже она показана выделенной зелёным точкой.

Когда слизняк качается обратно в другом направлении, то верёвка снова должна отцепиться в той же точке (выделенной на рисунке выше красным цветом):

Логика раскручивания

Чтобы вычислить момент, когда нужно раскрутить верёвку в точках, об которые она оборачивалась ранее, нам потребуются знания геометрии. В частности, нам пригодится сравнение углов для определения того, когда верёвка должна отцепиться от ребра.

Эта задача может показаться немного пугающей. Математика способна вселять ужас и отчаянье даже в самых отважных.

К счастью, в Unity есть отличные вспомогательные математические функции, которые способны немного упростить нашу жизнь.

Откройте в IDE скрипт RopeSystem и создайте новый метод под названием HandleRopeUnwrap().

private void HandleRopeUnwrap()
{

}

Перейдите к Update() и добавьте в самый конец вызов нашего нового метода.

HandleRopeUnwrap();

Пока HandleRopeUnwrap() ничего не делает, но теперь мы сможем обрабатывать логику, связанную со всем процессом отцепления от рёбер.

Как вы помните из первой части туториала, мы хранили позиции оборачивания верёвки в коллекции с названием ropePositions, которая является коллекцией List<Vector2>. Каждый раз, когда верёвка оборачивается вокруг ребра, мы сохраняем в эту коллекцию позицию этой точки оборачивания.

Чтобы процесс был более эффективным, мы не будем выполнять никакую логику в HandleRopeUnwrap(), если количество сохранённых в коллекции позиций равно или меньше 1.

Другими словами, когда слизняк прицепился к начальной точке и его верёвка пока не оборачивалась вокруг рёбер, количество ropePositions будет равно 1, и мы не будем выполнять логику обработки раскручивания.

Добавьте этот простой оператор return в верхнюю часть HandleRopeUnwrap(), чтобы сэкономить драгоценные циклы ЦП, потому что этот метод вызывается из Update() много раз в секунду.

if (ropePositions.Count <= 1)
{
    return;
}

Добавление новых переменных

Под этой новой проверкой мы добавим несколько измерений и ссылок на различные углы, необходимых для реализации основы логики раскручивания. Добавим в HandleRopeUnwrap() следующий код:

// Hinge = следующая точка вверх от позиции игрока
// Anchor = следующая точка вверх от Hinge
// Hinge Angle = угол между anchor и hinge
// Player Angle = угол между anchor и player

// 1
var anchorIndex = ropePositions.Count - 2;
// 2
var hingeIndex = ropePositions.Count - 1;
// 3
var anchorPosition = ropePositions[anchorIndex];
// 4
var hingePosition = ropePositions[hingeIndex];
// 5
var hingeDir = hingePosition - anchorPosition;
// 6
var hingeAngle = Vector2.Angle(anchorPosition, hingeDir);
// 7
var playerDir = playerPosition - anchorPosition;
// 8
var playerAngle = Vector2.Angle(anchorPosition, playerDir);

Здесь куча переменных, поэтому я объясню каждую из них, а также добавлю удобную иллюстрацию, которая позволит разобраться в их предназначении.

1. anchorIndex — это индекс в коллекции ropePositions в двух позициях от конца коллекции. Мы можем рассматривать его как точку в двух позициях на верёвке от позиции слизняка. На рисунке ниже это оказывается первая точка крепления крюка к поверхности. В процессе заполнения коллекции ropePositions новыми точками оборачивания эта точка будет всегда оставаться точкой оборачивания на расстоянии двух позиций от слизняка.
2. hingeIndex — это индекс коллекции, в котором хранится точка текущего шарнира; другими словами, позиция, в которой верёвка в данный момент оборачивается вокруг точки, ближайшей к концу верёвки со стороны слизняка. Она всегда находится на расстоянии одной позиции до слизняка, поэтому мы и используем ropePositions.Count - 1.
3. anchorPosition вычисляется выполнением ссылки на место anchorIndex в коллекции ropePositions и является простым значением Vector2 этой позиции.
4. hingePosition вычисляется выполнением ссылки на место hingeIndex в коллекции ropePositions и является простым значением Vector2 этой позиции.
5. hingeDir — это вектор, направленный из anchorPosition в hingePosition. Он используется в следующей переменной для получения угла.
6. hingeAngle — здесь применяется полезная вспомогательная функция Vector2.Angle() для вычисления угла между anchorPosition и точкой шарнира.
7. playerDir — это вектор, направленный из anchorPosition в текущую позицию слизняка (playerPosition)
8. Затем с помощью получения угла между опорной точкой и игроком (слизняком) вычисляется playerAngle.

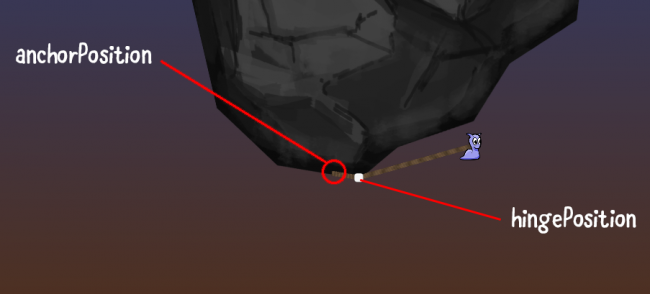
Все эти переменные вычисляются с помощью позиций, сохранённых как значения Vector2 в коллекции ropePositions и сравнением этих позиций с другими позициями или текущей позицией игрока (слизняка).

Двумя важными переменными, используемыми для сравнения, являются hingeAngle и playerAngle.

Значение, хранящееся в hingeAngle, должно оставаться статическим, потому что это всегда постоянный угол между точкой на расстоянии двух «сгибов верёвки» от слизняка и текущим «сгибом верёвки», ближайшим к слизняку, который не движется, пока верёвка не раскрутится или после сгиба не будет добавлена новая точка сгиба.

При качании слизняка меняется playerAngle. Сравнивая этот угол с hingeAngle, а также проверяя, находится ли слизняк слева или справа от этого угла, мы можем определить, должна ли отцепляться текущая точка сгиба, ближайшая к слизняку.

В первой части этого туториала мы сохраняли позиции сгибов в словаре под названием wrapPointsLookup. При каждом сохранении точки сгиба мы добавляли её в словарь с позицией в качестве ключа и с 0 в качестве значения. Однако это значение 0 было довольно загадочным, правда?

Это значение мы будем использовать для хранения позиции слизняка относительно его угла с точкой шарнира (текущей ближайшей к слизняку точки сгиба).

Если присвоить значение -1, то угол слизняка (playerAngle) меньше угла шарнира (hingeAngle), а при значении 1 угол playerAngle больше, чем hingeAngle.

Благодаря тому, что мы сохраняем значения в словаре, каждый раз, когда мы сравниваем playerAngle с hingeAngle, мы можем понять, прошёл ли слизняк только что через предел, после которого верёвка должна отцепиться.

Можно объяснить это иначе: если угол слизняка только что проверили и он меньше угла шарнира, но в последний раз, когда его сохраняли в словарь точек сгибов он был помечен значением, обозначающим, что он находился на другой стороне этого угла, то точку немедленно нужно удалить!

Отцепление верёвки

Посмотрите на показанный ниже скриншот с примечаниями. Наш слизняк прицепился к скале, раскачался вверх, на пути вверх обернув верёвку вокруг ребра скалы.

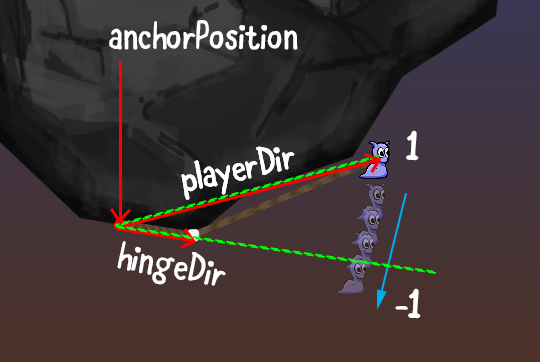
Можно заметить, что в самой верхней позиции раскачивания, где слизняк непрозрачен, его текущая ближайшая точка сгиба (помеченная белой точкой) будет сохранена в словаре wrapPointsLookup со значением 1.

На пути вниз, когда playerAngle становится меньше hingeAngle (две пунктирных зелёных линии), как показано синей стрелкой, выполняется проверка, и и если последнее (текущее) значение точки сгиба было равно 1, то точку сгиба нужно убрать.

Теперь давайте реализуем эту логику в коде. Но прежде чем приступить, давайте создадим болванку метода, который будем использовать для раскручивания. Благодаря этому после создания логики она не будет приводить к ошибке.

Добавим новый метод UnwrapRopePosition(anchorIndex, hingeIndex), вставив следующие строки:

private void UnwrapRopePosition(int anchorIndex, int hingeIndex)
{

}

Сделав это, вернёмся к HandleRopeUnwrap(). Под недавно добавленными переменными добавим следующую логику, которая будет обрабатывать два случая: playerAngle меньше hingeAngle и playerAngle больше hingeAngle:

if (playerAngle < hingeAngle)
{
    // 1
    if (wrapPointsLookup[hingePosition] == 1)
    {
        UnwrapRopePosition(anchorIndex, hingeIndex);
        return;
    }

    // 2
    wrapPointsLookup[hingePosition] = -1;
}
else
{
    // 3
    if (wrapPointsLookup[hingePosition] == -1)
    {
        UnwrapRopePosition(anchorIndex, hingeIndex);
        return;
    }

    // 4
    wrapPointsLookup[hingePosition] = 1;
}

Этот код должен соответствовать объяснению описанной выше логики для первого случая (когда playerAngle < hingeAngle), но также обрабатывает и второй случай (когда playerAngle > hingeAngle).

1. Если текущая ближайшая к слизняку точка сгиба имеет значение 1 в точке, где playerAngle < hingeAngle, то мы убираем эту точку и выполняем возврат, чтобы остальная часть метода не выполнялась.
2. В противном случае, если точка сгиба в последний раз не была помечена значением 1, но playerAngle меньше hingeAngle, то присваивается значение -1.
3. Если текущая ближайшая к слизняку точка сгиба имеет значение -1 в точке, где playerAngle > hingeAngle, то убираем точку и выполняем возврат.
4. В противном случае мы присваиваем записи словаря точек сгибов в позиции шарнира значение 1.

Этот код гарантирует, что словарь wrapPointsLookup всегда обновляется, обеспечивая соответствие значения текущей точки сгиба (ближайшей к слизняку) текущему углу слизняка относительно точки сгиба.

Не забывайте, что значение равно -1, когда угол слизняка меньше, чем угол шарнира (относительно опорной точки), и равно 1, когда угол слизняка больше, чем угол шарнира.

Теперь дополним UnwrapRopePosition() в скрипте RopeSystem кодом, который непосредственно займётся отцеплением, перемещая опорную позицию и присваивая значению расстояния верёвки DistanceJoint2D новое значение расстояния. Добавим в созданную ранее болванку метода следующие строки:

    // 1
    var newAnchorPosition = ropePositions[anchorIndex];
    wrapPointsLookup.Remove(ropePositions[hingeIndex]);
    ropePositions.RemoveAt(hingeIndex);

    // 2
    ropeHingeAnchorRb.transform.position = newAnchorPosition;
    distanceSet = false;

    // Set new rope distance joint distance for anchor position if not yet set.
    if (distanceSet)
    {
        return;
    }
    ropeJoint.distance = Vector2.Distance(transform.position, newAnchorPosition);
    distanceSet = true;

1. Индекс текущей опорной точки (вторая позиция верёвки от слизняка) становится новой позицией шарнира, а старая позиция шарнира удаляется (та, которая ранее была ближайшей к слизняку и которую мы сейчас «раскручиваем»). Переменной newAnchorPosition присваивается значение anchorIndex в списке позиций верёвки. Далее оно будет использовано для расположения обновлённой позиции опорной точки.
2. RigidBody2D шарнира верёвки (к которому прикреплён DistanceJoint2D верёвки) изменяет свою позицию на новую позицию опорной точки. Это обеспечивает плавное непрерывное движение слизняка на верёвке, когда он соединён с DistanceJoint2D, а это соединение должно позволить ему продолжать качаться относительно новой позиции, которая стала опорной — другими словами, относительно следующей точки вниз по верёвке от его позиции.
3. Затем необходимо обновить значение расстояния DistanceJoint2D, чтобы учесть резкое изменение расстояния от слизняка до новой опорной точки. Если это ещё не сделано, то выполняется быстрая проверка флага distanceSet, и расстоянию присваивается значение вычисленного расстояния между слизняком и новой позицией опорной точки.

Сохраните скрипт и вернитесь в редактор. Запустите игру снова и понаблюдайте за тем, как верёвка отцепляется от рёбер, когда слизняк проходит пороговые значения каждой точки сгиба!

Хотя логика уже готова, мы добавим немного вспомогательного кода в HandleRopeUnwrap() прямо перед сравнением playerAngle с hingeAngle (if (playerAngle < hingeAngle)).

if (!wrapPointsLookup.ContainsKey(hingePosition))
{
    Debug.LogError("We were not tracking hingePosition (" + hingePosition + ") in the look up dictionary.");
    return;
}

На самом деле этого не должно происходить, потому что мы переопределяем и отсоединяем крюк-кошку, когда она оборачивается вокруг одного ребра дважды, но если это всё-таки произойдёт, нам не сложно выйти из этого метода с помощью простого оператора return и сообщения об ошибке в консоли.

Кроме того, благодаря этому мы удобнее будем обрабатывать подобные предельные случаи; более того, мы получаем собственное сообщение об ошибке в случае, когда происходит что-то ненужное.

Куда двигаться дальше?

Вот ссылка на готовый проект этой второй и последней части туториала.

Поздравляю с прохождением этой серии туториалов! Когда дело дошло до сравнения углов и позиций, всё стало довольно сложно, но мы это пережили и теперь у нас есть замечательная система крюка-кошки и верёвок, которая способна накручиваться на объекты в игре.

Знаете ли вы, что наша команда разработчиков Unity написала книгу? Если нет, то посмотрите Unity Games By Tutorials. Эта игра научит вас создавать с нуля четыре готовые игры:

• Шутер с двумя стиками
• Шутер от первого лица
• Игра tower defense (с поддержкой VR!)
• 2D-платформер

Прочитав эту книгу, вы научитесь создавать собственные игры для Windows, macOS, iOS и других платформ!

Эта книга предназначена как для новичков, так и для тех, кто хочет повысить свои навыки в Unity до профессионального уровня. Для освоения книги вам нужно иметь опыт программирования (на любом языке).

Автор: PatientZero

Источник