Управляемость сложных сетей — перевод статьи Controllability of complex networks

Данная статья представляет собой перевод статьи Альберта Барабаши и его соавторов, под названием «Controllability of complex networks». Оригинал которой в формате PDF можно скачать здесь.

Кстати сказать, некоторые считают, что Эйнштейна XXI века будут тоже звать Альберт. А именно Альберт Барабаши.

Для тех, кто уважает чужой труд, напомню, что перевод является авторским, и любое цитирование или упоминание требует указания ссылки на оригинал перевода. Надеюсь, что те, кто не уважают чужой труд, не заморачивают себе голову тем, о чем будет идти речь в статье.

В переводе, жирным шрифтом будут выделены важные заключения и основные понятия, приведенные в статье, выделенные автором перевода. Курсивом будут выделены комментарии автора перевода и ссылки на определения и дополнительную информацию по некоторым понятиям и методам, приведенным в статье.

Управляемость сложных сетей

Доказательством того, что мы полноценно понимаем природные и техногенные системы может служить лишь наша способность управлять этими системами. Несмотря на то, что теория управления предлагает математические инструменты для управления инженерными и природными системами для перевода их к желаемому состоянию, единой инфраструктуры для управления сложными самоорганизующимися системами не существует. В этой статье мы разрабатываем аналитические инструменты для исследования управляемости произвольных комплексных ориентированных сетей, а также определения набора узлов-драйверов с управлением, зависящим от времени, которое может целенаправленно управлять динамикой всей системы. Мы применили эти средства для нескольких реальных сетей, установив, что число узлов-драйверов в основном определяется степенью распределения сети (network’s degree distribution). Мы покажем, что сложнее всего контролировать разряженные неоднородные сети, которые появляются во многих реальных сложных системах, а плотными и однородными сетями можно управлять с помощью всего-лишь нескольких узлов-драйверов. Парадоксально, но мы выяснили, что как и в модели, так и в реальных системах, узлы-драйверы, как правило, не обладают высокой степенью узлов (degree nodes, количество входных или выходных связей).

Согласно принципам теории управления, динамическая система является управляемой, если при определенном наборе входных переменных, она может быть переведена из любого начального состояния в любое желаемое состояние за конечное время^1-3. Это определение согласуется с нашим интуитивным пониманием контроля, имея возможность привести систему к желаемому состоянию через соответствующие манипуляции нескольких входных переменных, подобно тому, как водитель, манипулируя педалями и рулевым колесом заставляет автомобиль двигаться с желаемой скоростью и в заданном направлении. Несмотря на то, что теория управления является математически  высокоразвитой отраслью техники с приложениями для электрических  схем, производственных процессов, коммуникационных систем^4-6, самолетостроения, космических аппаратов и роботов^2-3, фундаментальные вопросы, связанные с управляемостью сложных систем, возникающих в природе и технике имеют сложности в разрешении. Трудность заключается в том, что неоходимо управлять двумя независимыми факторами, каждый со своим собственным уровнем неизвестности:

(1) архитектура системы, представленная сетью, инкапсулирующей то, какие компоненты взаимодействуют между собой,
(2)  динамические правила, которые фиксируют зависящие от времени взаимодействия между компонентами.

Таким образом, прогресс может быть возможен только в системах, в которых оба слоя хорошо очерчены, таких как управление синхронизированными сетями^7-10, небольшие биологические цепи и управление скоростью для коммуникационных сетей^4-6. Последние достижения в направлении сведения качественных топологических характеристик сложных сетей к количественным^12-16 пролили свет на фактор (1),  указав нам на то, что некоторые сети легче контролировать чем другие, и как влияет топология сети на управляемость системой. Несмотря на некоторые концептуально новаторские работы^17-23 (см. раздел II Дополнительной  Информации), нам по-прежнему не хватает главных ответов на эти  вопросы для крупных взвешенных и направленных сетей, которые чаще всего возникают в сложных системах.

Управляемость сети

В основе большинства реальных систем лежат нелинейные процессы, но управляемость нелинейных систем во многих отношениях структурно похожа на управляемость линейных систем³, что побудило нас начать исследования с использования уравнений канонической линейной динамики инвариантной по времени
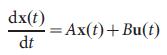(1)
где вектор X (t) = (X1 (t), ..., Xn (t)) фиксирует состояние системы, состоящей из N узлов в момент времени t. Например, X (t) может обозначать количество трафика, который проходит через узел i в коммуникационной сети²⁴ или концентрацию фактора транскрипции в сети регуляции генов²⁵. Матрица A размерности NхN описывает схему соединений системы и силы взаимодействия между компонентами, например, трафик на отдельных линиях связи или силу взаимодействия регулирования. Наконец, В представляет собой входную матрицу размерности MхN (M<=N), которая идентифицирует узлы, которые управляются внешним контроллером. Система управляется с помощью входного вектора U (t) = (U1 (t), ...,Uм (t)) зависящего от времени t, введенного с помощью контроллера (рис. 1а), где, вобще говоря один и тот же сигнал Ui(t) может управлять несколькими узлами.

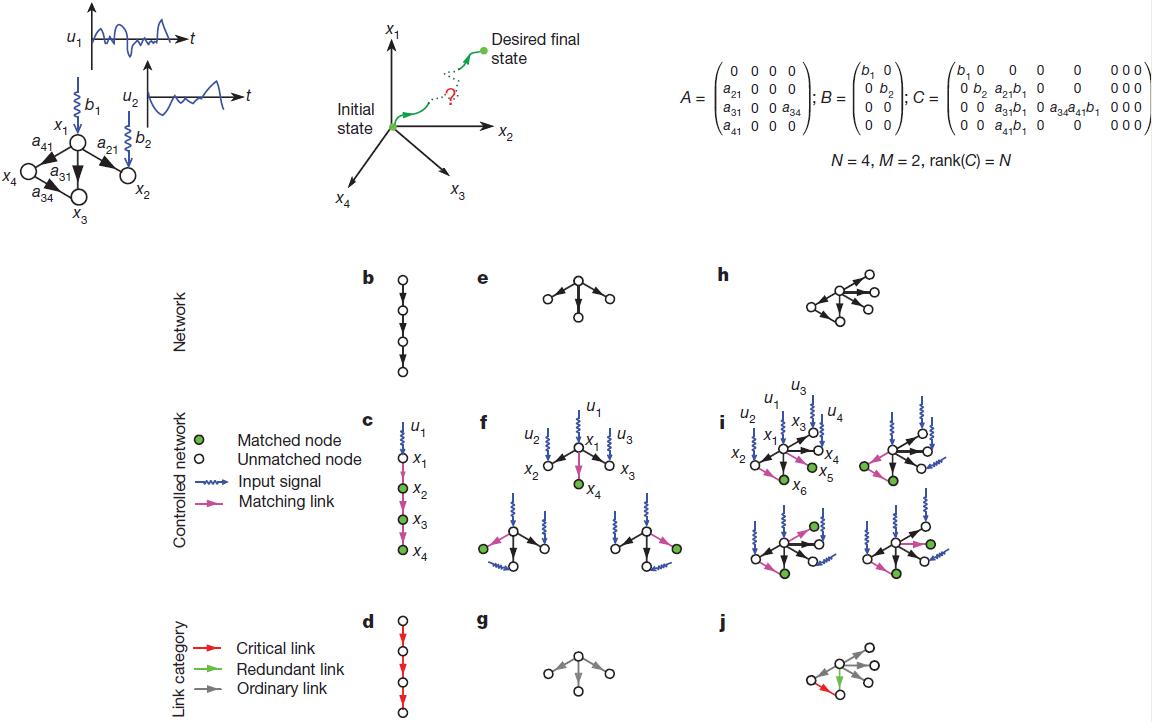
Рисунок 1 | управление простой сетью. a, Небольшая сеть может контролироваться входным вектором 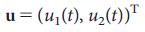(слева), что позволяет нам переместить сеть из ее исходного состояния в некоторое желаемое конечное состояние в пространстве состояний (справа). Уравнение (2) обеспечивает управляемость матрицы (С), которая в данном случае имеет полный ранг, указывая, что система управляема. b, Простая сетевая модель: ориентированная траектория. c, максимальное паросочетание ориентированной траектории. Насыщенные связи показаны фиолетовым цветом, насыщенные узлы — зеленым, а свободные — белым. Уникальный максимальное паросочетание узлов включает в себя все связи, такие, что никто из них не являются ни начальными ни конечными узлами. Только верхний узел — свободный, поэтому контроль над ним дает полный контроль над ориентированной траекторией ( 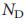= 1). d, В направленной траектории показанной на рисунке b, все cсылки являются критическими, то есть их удаление лишит нас способности контролировать сеть. е, Малая сетевая модель: направленная звезда. f, Максимальное паросочетание в направленной звезде. Только одна связь может быть частью максимального паросочетания, которое дает три свободных узла ( 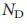= 3). Три различных максимальных паросочетания показывают, что три различные конфигурации узлов могут осуществлять полный контроль. g, В ориентированной звезде, все связи обычные, то есть, их удаление может лишить некоторых конфигураций управления, но сетью можно управлять в их отсутствии с тем же числом узлов-драйверов 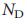. h, Пример небольшой сети. i, Только две связи могут быть частью максимального паросочетания для сети h, что дает четыре свободных узла ( 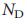= 4). Есть всего четыре различных максимальных паросочетания для этой сети. j, Cеть имеет одну критическую связь, одну излишнюю связь (которая может быть удалена без потери какой-либо конфигурации управления) и четыре обычных связи.

Если мы хотим управлять системой, то в первую очередь нам необходимо определить набор узлов, управляя которыми с помощью различных сигналов, мы сможем обеспечить полный контроль над сетью. Мы будем называть эти узлы драйверами. Особенно интересно определить минимальное число драйверов, контроля над которыми будет достаточно для того, чтобы полностью контролировать динамику системы. Обозначим его Nd.

Система, описываемая уравнением (1) называется управляемой, если ее можно привести из любого начального состояния в любое желаемое конечное состояния за конечное время, что возможно тогда и только тогда, когда матрица 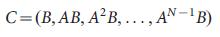(2) размерности N x NM, имеет полный ранг 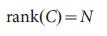(3)

Это уравнение представляет собой математическое условие управляемости системы, и называется критерием управляемости Калмана по рангу^1,2 (рис. 1а). В практическом смысле, управляемость также можно рассматривать следующим образом, определить такое минимальное количество узлов-драйверов, что уравнение (3) будет выполняться. Так, например, уравнение (3) говорит о том, что контроль над узлом x1 на рис. 1b с помощью входного сигнала u1 обеспечивает полный контроль над системой, так как состояния узлов x1, x2, x3 и x4 однозначно определяются сигналом u1 (t) (рис. 1c). В тоже время, наоборот, воздействия на верхний узел на рис. 1e не будет достаточно для полного управления, так как разница 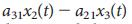(где aij являются элементами матрицы A) не может быть однозначно определена с помощью u1 (t) (см. рис. 1f и раздел III.А Дополнительной  Информации). Чтобы получить полный контроль, мы одновременно должны управлять узлом x1 и двумя любыми другими узлами среди {x2, x3, x4} (см. рис. 1h, i для более сложного примера).

Для того, чтобы применить уравнения (2) и (3) к произвольной сети, необходимо знать вес каждой связи (то есть, aij), которые для большинства реальных сетей или неизвестны (например сети регуляции), либо известны лишь приблизительно и зависят от времени (например Интернет-трафик). Даже если все веса известны, поиск по методу грубой силы требует, чтобы мы вычислили ранг матрицы C для 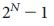разных комбинаций, что является чрезмерно сложной с вычислительной точки зрения задачей для крупных сетей. Чтобы обойти необходимость измерения веса ссылки, отметим, что система (A, B) является «структурно контролируемой»²⁶ если возможно выбрать ненулевые веса в А и В так, что система удовлетворяет уравнению (3). Структурно управляемая система может быть контролируемой почти для всех комбинациий значений весовых коэффициентов за исключением некоторых патологических случаев с нулевой мерой, которые происходят тогда, когда параметры системы удовлетворяют некоторым случайным ограничениям^{26, 27}. Таким образом, структурная управляемость помогает нам преодолеть по сути наше неполное знание о весах связей в А. Кроме того, поскольку структурная управляемость подразумевает управляемость континуума линеаризованных систем²⁸, наши результаты также могут обеспечить достаточное условие управляемости для большинства нелинейных систем³ (раздел III.A Дополнительной  Информации).

Чтобы избежать поиска узлов-драйверов методом грубой силы, мы доказали, что минимальное число входов или узлов-драйверов, необходимое для поддержания полного управления над сетью определяется «максимальным паросочетанием» в сети, то есть максимальным набором связей, которые не включают начальных или конечных узлов (рис. 1 c, f, i). Узел называют насыщенным, если связь указывает на точки максимального паросочетания, иначе она свободна. Как мы показали в Дополнительной  Информации, проблема структурной управляемости соответствует эквивалентной геометрической задаче в сети: мы можем получить полный контроль над ориентированной сетью, тогда и только тогда, когда мы непосредственно управляем каждым свободным узлом, и есть направленные пути от входных сигналов для всех насыщенных узлов²⁹. Возможность определения 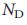, с использованием этого отображения является нашим первым основным результатом. Поскольку максимальное паросочетание в ориенированных сетях численно может быть определено за число шагов не более 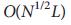³⁰, где L обозначает количество связей, отображение предлагает эффективный метод определения узлов-драйверов для произвольной ориентированной сети.

Управляемость реальных сетей

Мы использовали инструменты, разработанные ранее, для изучения управляемости нескольких реальных сетей. Сети были выбраны из-за их разнообразия: например, целью генной сети регуляции является контроль динамики клеточных процессов, поэтому ожидалось, что в результате получится структура, которая является эффективной с точки зрения контроля, и теоретически должна иметь небольшое количество узлов-драйверов (то есть малое 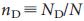). Напротив, для управляемости всемирной паутины или сетей цитирования подобного ожидать не приходится, что делает этот вопрос трудным даже для оценки 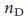. Наконец, можно было бы утверждать, что социальные сети, учитывая их нейтральность к восприятию (или даже сопротивляемость) для управления, должны иметь высокий 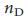, так как в них необходимо контролировать большинство людей по отдельности, чтобы контролировать всю систему. Мы использовали отображение в максимальное паросочетание для того, чтобы определить минимальный набор узлов-драйверов 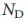для сетей из Таблицы 1. Полученные данные противоречат нашим ожиданиям: как группа, генные сети регуляции проявляют высокий 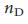(0,8), указывая нам, на то, что необходимо независимо контролировать около 80% узлов для контроля их в полном объеме. Напротив, некоторые социальные сети характеризуются минимальными значениями 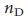, что говорит о том, что несколько человек, в принципе, могут контролировать всю систему.

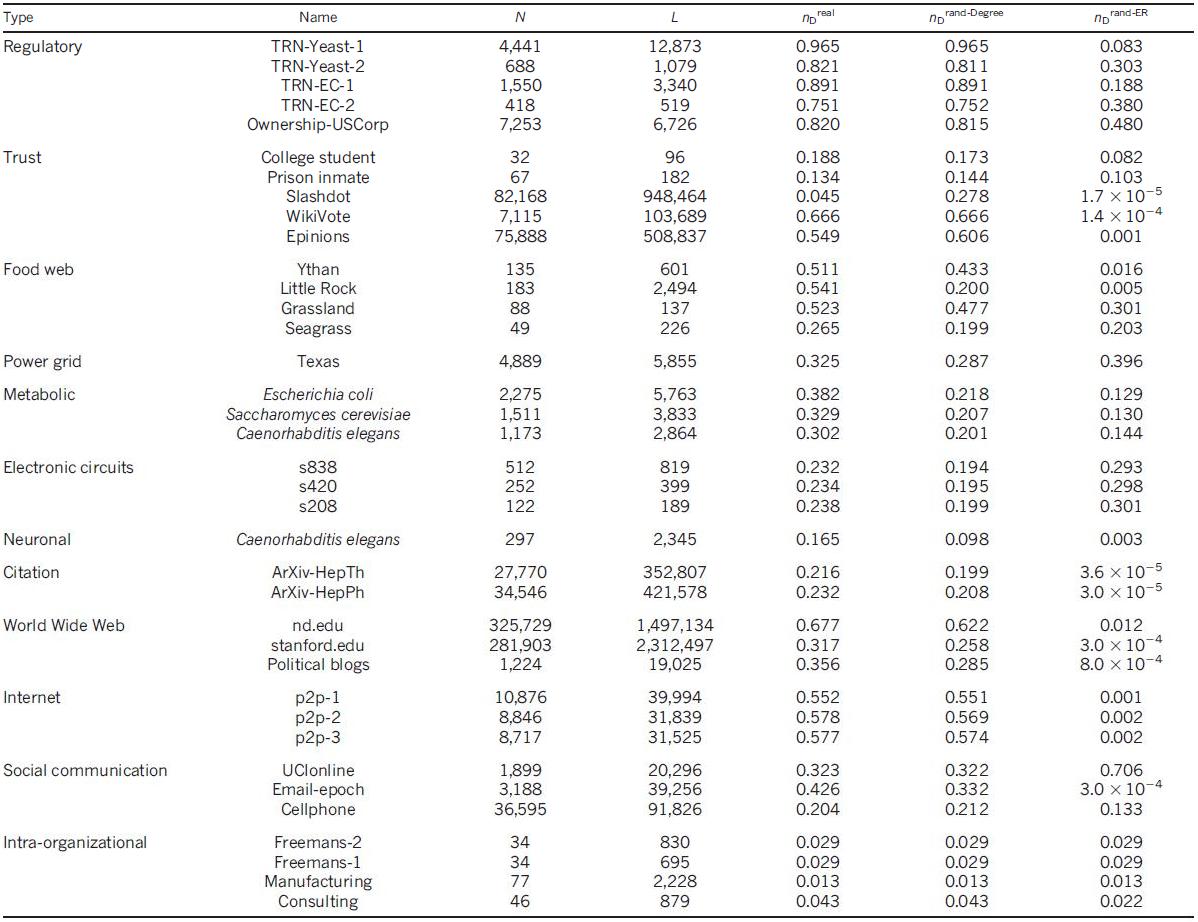
Таблица 1 | Характеристики реальных сетей проанализированных в данной статье

Для каждой сети, указан ее тип и имя; количество узлов (N) и связей (L); плотность узлов-драйверов, расчитанная в реальной сети 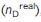, после рандомизации с сохранением степеней 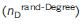и после полной рандомизации . Для доступа к источникам данных и ссылками, смотри секцию VI Дополнительной  Информации.

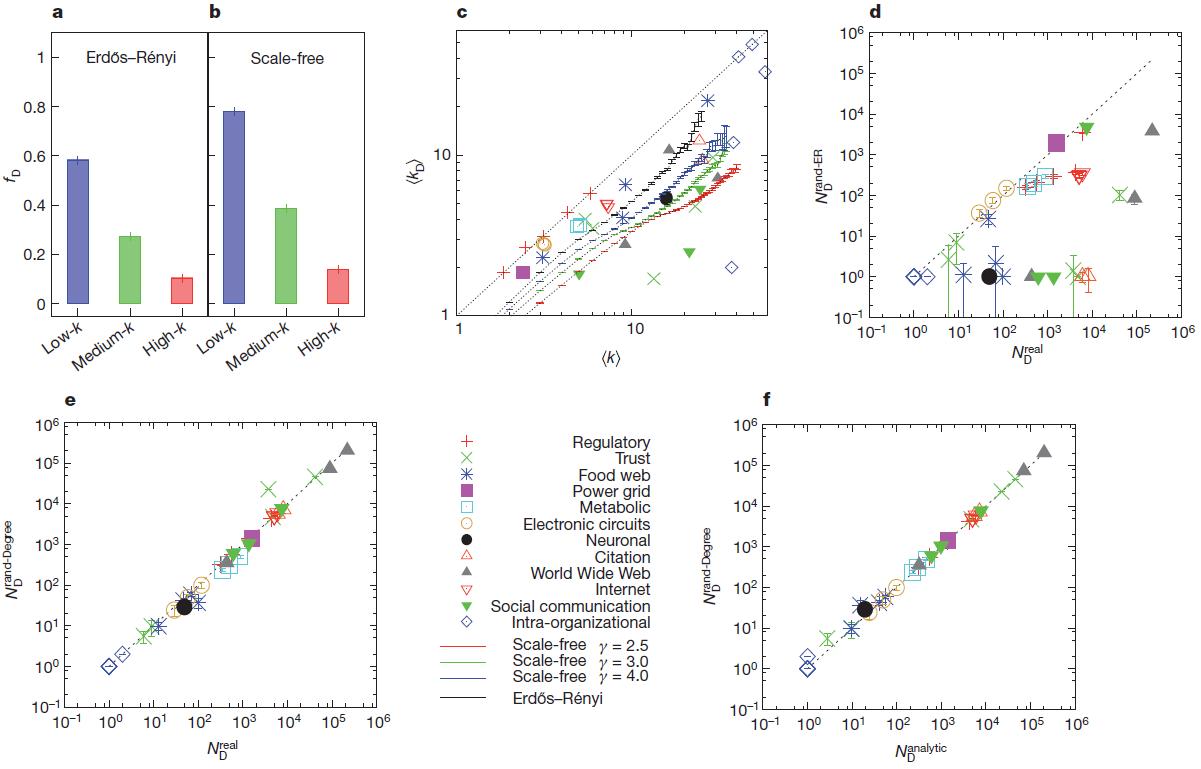
Учитывая, что хабы (узлы с высокой степенью) имеют важную роль в поддержании структурной целостности сети от сбоев и внешних воздействий^31,32 в явлениях распространения^32,33 и в синхронизации^8,34, было бы естественно предположить, что контроль над хабами необходим для управления всей сетью. Для проверки правильности этой гипотезы, мы разделили узлы на три группы равного размера в зависимости от их степени, k (низкая, средняя и высокая). Как показывает рис. 2a, b для двух канонических сетевых моделей (Erdos-Renyi^35,36 и безмасштабных^15,37-39), доля узлов-драйверов значительно выше среди узлов с низкой степенью чем среди хабов. На рис. 2c, представлен график зависимости средней степени узлов-драйверов, 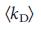, от средней степени, 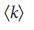, для каждой сети из таблицы 1, для нескольких сетевых моделей. Во всех случаях 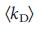значительно меньше, чем аналогичные 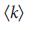, указывая на то, что в реальных и моделируемых системах узлы-драйверы, как правило не являются хабами.

Чтобы определить топологические особенности, которые определяют управляемость сети, мы выбрали случайное состояние каждой реальной сети с использованием процедуры полной рандомизации (RAND-ER), которая превращает сеть в ориентированную случайную сеть ErdoS-Renyi с N и L постоянными. Для нескольких сетей нет никакой корреляции между 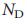исходной сети и 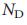его рандомизированного состояния (рис. 2d), таким образом, при полной рандомизации методом исключения, мы приходим к выводу о том, что топологические характеристики не влияют на управляемость. Мы также применили рандомизацию с сохранением степеней ^40,41(RAND-degree), которая сохраняет входную степень, 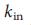, и выходную степень, 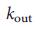, каждого узла неизменными, но выбирает случайным образом узлы, которые связаны друг с другом. Мы считаем, что несмотря на наблюдаемые различия в шесть порядков для величины 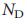эта процедура не изменяет 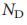существенно. Таким образом, управляемость системы в значительной степени зависит от распределения степеней узлов сети 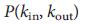, что является нашим вторым и наиболее значимым выводом. Он говорит о том, что 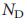в основном определяется числом входящих и исходящих связей каждого узла и не зависит от того, куда указывают связи.

Аналитический подход к управляемости

Важность распределения степеней, позволяет аналитическим путем определить 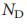для сети с произвольными 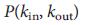. Используя метод седловой точки^42-44, мы получили набор самосогласованных уравнений (раздел IV, Дополнительной  Информации), входом которых является распределение степеней, а решение которых для среднего 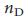(или 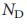) для всех реализаций сетей совместимо с 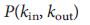, что является нашим третьим ключевым результатом. Как показывает рис. 2 f, аналитически расчитанный 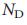полностью согласуется с (а следовательно, должен хорошо согласовываться и с точным значением 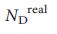), что предоставляет нам эффективный аналитический инструмент для изучения влияния различных параметров сети на 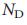. Хотя метод седловой точки не предлагает аналитического решения, мы можем получить зависимость 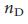от ключевых параметров сети в термодинамическом пределе 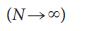. Например, мы выяснили, что для ориентированной сети ErdoS-Renyi 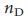при больших 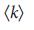справедливо 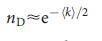(4). Для безмасштабных сетей в пределе, для больших 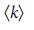³⁸, с показателем степени 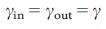мы емеем уравнение 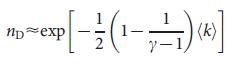(5), которое в пределе 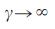имеет такую же зависимость от 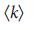, как и уравнение (4). Из уравнение (5) следует, что 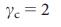является критическим показателем для управляемости бесконечных безмасштабных сетей, и только для 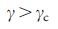мы можем контролировать всю систему через конечное количество узлов (то есть 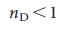). Для 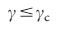, в термодинамическом пределе, абсолютно все узлы должны контролироваться (то есть, 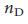= 1). Отметим, что 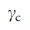отличается от 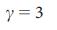, которое является критическим показателем для ряда сетевых явлений, от устойчивости до вирусного распространения^31-33,45, обусловленных расхождением 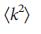. Для проверки аналитических расчетов для сетей типа ErdoS-Renyi и безмасштабных сетей, мы определили численную зависимость 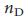от 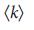, которая подтверждает асимптотическую экспоненциальную зависимость 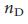от 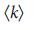, что и предсказывают уравнения (4) и (5). Кроме того, прогнозируемое значение 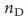хорошо согласуется с численными результатами для 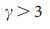(Рис. 3 d, e). Тем не менее, в окрестности 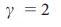, , 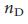как и предсказывалось методом седловой точки, отклоняется от точного значения 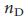вследствие корреляции степеней, которые значительны для 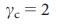, и могут быть устранены путем введения обрезанной степени при построении безмасштабных сетей^39,46 (раздел IV.В Дополнительной  Информации). Уравнение (5) также показывает, что 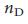уменьшается с увеличением 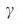(при фиксированных 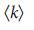), указывая на то, что 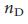зависит от неоднородности степени, представляющей разницу между менее связаннными и более связанными узлами. 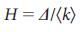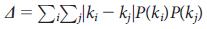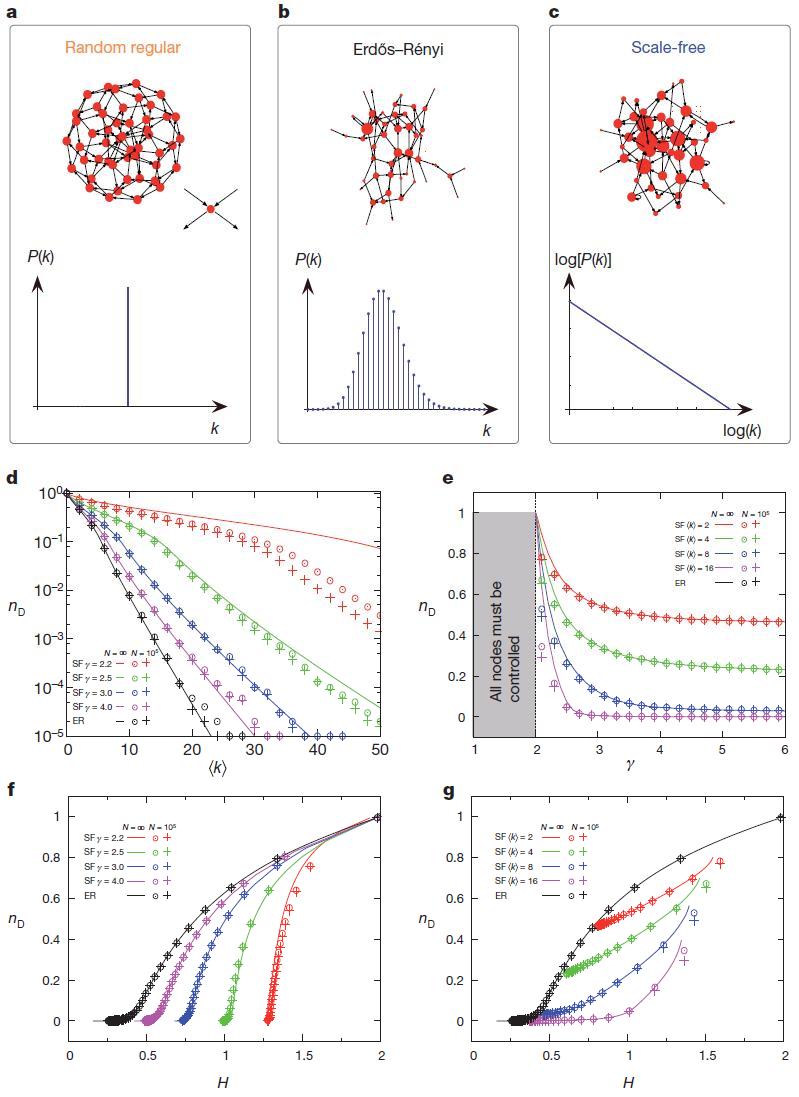Мы определили неоднородность степени, как , где является средней абсолютной разницей степеней для всех пар узлов (i и j) взятых из распределения степени 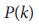. Неоднородность степени равна нулю (H = 0) для сетей, у которых все узлы имеют одинаковую степень, например случайные регулярные ориентированные графы (Рис. 3 a), в которых входные и выходные степени узлов приведены к 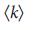/ 2, но узлы соединены случайным образом. Для 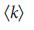>= 2, этот граф всегда имеет совершенное паросочетание⁴⁷ (паросочетание, содержащее все вершины графа), что означает то, что один узел-драйвер может управлять всей системой (раздел IV.B1 Дополнительной  Информации).

Рисунок 2 | Характеристики и предсказание поведения узлов-драйверов ().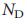
a, b, роль хабов в сетевой модели. Столбики показывают долю узлов-драйверов, 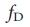, среди узлов с низкой, средней и высокой степенью узлов для двух сетевых моделей, Erdos-Re'nyi (а) и бесмасштабных (b), с N=10⁴ 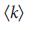= 3 (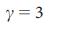), указывая нам на то, что узлы-драйверы, как правило не являются хабами. ErdoS-Re'nyi и безмасштабные сети генерируются от статической модели³⁸ и результаты усредненны по 100 реализациям. Столбики ошибок (над основными столбиками), как показано на рисунке, меньше чем сами значения. с, средняя степень узлов-драйверов по сравнению со средней степенью всех узлов в реальных и модельных сетях, указывает на то, что в реальных системах хабы не являются узлами-драйверами. d, Количество узлов-драйверов 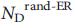, полученное для полностью рандомизированных версий сетей, перечисленных в таблице 1, по сравнению с точным значением, 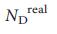. e, Количество узлов-драйверов , полученное с сохранением степени для рандомизированных версий сетей, показанных в таблице 1, по сравнению 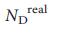. f, Аналитически рассчитанное 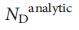, полученное с использованием метода седлововй точки, по сравнению с . В d-f, точки данных и погрешности (SEM) были определены из 1000 реализаций рандомизированных сетей.

Неоднородность степеней увеличивается по мере того, как мы переходим от случайного регулярного ориентированного графа к сети типа ErdoS-Renyi (Рис. 3 b), и в конечном итоге с уменьшением 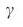к безмасштабным сетям (рис. 3 c). В целом, доля узлов-драйверов, 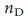, монотонно возрастает с H, при сохранении постоянным 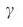(рис. 3 f) или 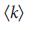(рис. 3 g).

Рисунок 3 | Влияние структуры сети на количество узлов-драйверов. a–c,
Характеристики исследуемых сетевых моделей. Случайно-ргулярный ориентированный граф (a), показанный здесь для 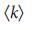= 4 является сетью с самым однородным распределением степеней, поскольку 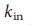= = 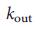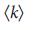/ 2 для всех узлов. Сети Erdos–Renyi networks (b) имеют распределение степеней по Пуассону, а разнородность степенй для них опредляется 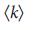. Безмасштабные сети (c) имеют степенную зависимость распредления степеней, что приводит к огромной разнородности степеней. d, плотность узлов-драйверов, 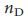, как функция от 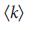для сетей Erdo–Renyi (ER) и безмасштабных (SF) с различными значениями 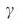. Как безмасштабные так и сети Erdos–Renyi генерируются из статической модели³⁸ с N = 10⁵. Линии являются аналитическими результатами и рассчитываются методом седловой точки с использованием ожидаемого в пределе 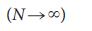распределения степеней.
Символы рассчитаны для построенной дискретной сети: кружки обозначают точные результаты расчета методом максимального паросочетания, и крестики обозначают аналитические результаты полученные методом седловой точки с использованием точной последовательности степеней построенной сети. Для больших 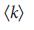, 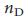приближается к нижней странице, N^-1, то есть к единственному узлу-драйверу 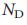= 1 в сети размера N. e, 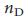как функция от 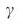для безмасштабных сетей с фиксированным 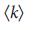. Для бесконечных безмасштабных сетей 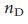-> 1, поскольку 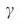-> 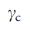= 2, то есть необходимо контроллировать почти все узлы для того, чтобы контролировать сеть целиком. Для конечных безмасштабных сетей, 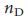-> 1 поскольку 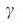-> 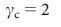, то есть необходимо контролировать почти все узлы для того чтобы контролировать сеть целиком. Для конечных безмасштабных сетей 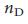достигает своего максимума, поскольку 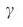приближается к 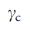(Дополнительная  Информация). f, 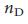как функция от разнородности степеней, H, для сетей Erdos–Renyi и безмасштабных ссетей с фиксированным 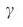и изменяющимся 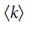. g, 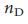nD как функция от H для сетей Erdos–Renyi и безмасштабных сетей для фиксированного 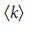и изменяющегося 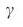. С увеличением 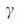, кривые сходятся к результату сетей ErdoS- Renyi (черный цвет) при соответствующем значении .
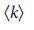Принимая во внимание эти результаты вместе, мы находим, что чем плотнее сеть, тем меньшее количество узлов-драйверов необходимо, чтобы контролировать ее, и что небольшие изменения в средней степени вызывают изменения 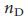масштабов порядка. Кроме того, чем больше разница между степенью узлов, тем большее количество узлов-драйверов необходимо для управления системой. В целом, сети, которые являются разряженными и неоднородными, а именно эти характиеристики как раз часто наблюдаются в сложных системах, таких как сотовые сети или Интернет, ^13-16 требуют больше узлов-драйверов, подчеркивая, что такие системы трудно контролировать.

Устойчивость управления

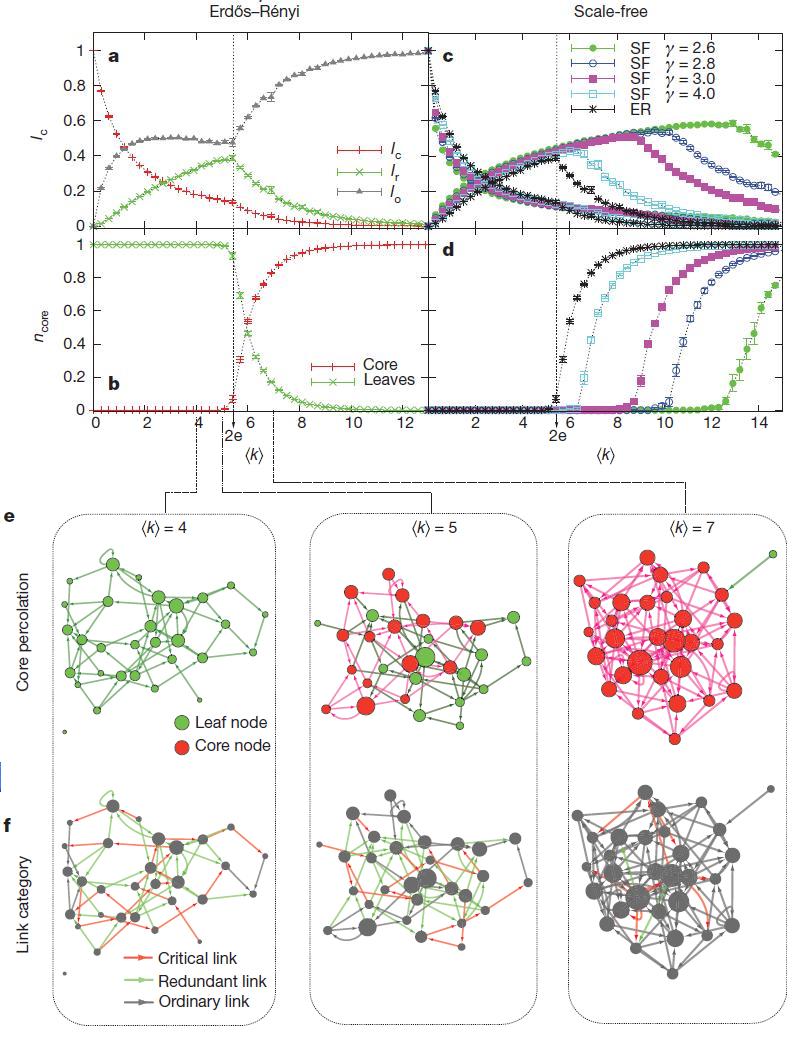
Чтобы увидеть, насколько надежна наша способность управлять сетью в ситуациях, когда пропадают некоторые связи в сети, которые возникают неизбежно, мы классифицируем каждую связь в одну из трех категорий (рис. 1, D, G, J):
«критическая», если в случае ее исчезновения нам нужно будет увеличить число узлов-драйверов для поддержания полной управляемости;
«лишняя», если она может быть удалена без ущерба для текущего набора узлов-драйверов, или
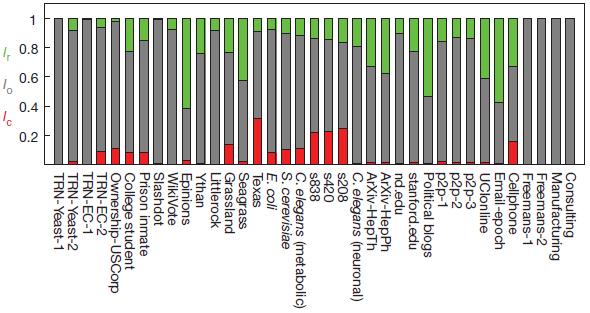
«обычная», если она не является ни критической, ни лишней. На рисунке 4 показаны плотности критических 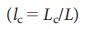, избыточных 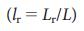и обычных 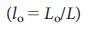связей для каждой реальной сети, и он показывает, что большинство сетей имеют малое количество или совсем не имеют критических связей. Большинство связей являются обычными, что означает, что они играют определенную роль в некоторых конфигурациях управления, но эти сети могут управляться и в их отсутствие.

Рисунок 4 | Категории ссылок в контексте устойчивости управления.
Доля критических (красные, LC), избыточных (зеленые, LR) и обычных (серые, LO) ссылок для реальных сетей обозначенных в Таблице 1. Для того чтобы сделать управление устойчивым к потере ссылок, достаточно удвоить только критические ссылки, формально делая каждую из этих ссылок избыточной, и таким образом убедиться, что нет критических ссылок в системе.

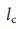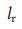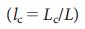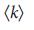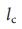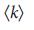
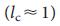
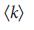
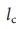
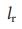
Для того, чтобы осознать факторы, которые определяют , и , на рис. 5 A, C, F мы показываем их зависимость для модельных систем. Поведение понять проще простого: для малых 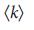, все связи имеют большое значение для управления . По мере того как увеличивается, избыточность сети увеличивается с уменьшением . Повышение избыточности предполагает, что плотность избыточных связей, , всегда должна увеличиваться с , но это не так: он достигает максимума при критическом значении 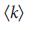, , 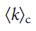после чего он падает. Это немонотонное поведение является результатом конкуренции двух топологически различных сегементов сети, ядра и листьев ⁴³. Ядро представляет собой компактный кластер узлов оставшихся в сети после применения процедуры «прожерливого» удаления листьев ⁴⁸, а листья являются узлами с 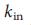= 1 или 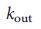= 1 до или во время удаления листьев. Ядро выходит через просачивание перехода (рис. 5, B, D): для К < 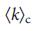, , так что система состоит только из листьев (рис. 5 E). При 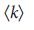= 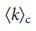, возникает небольшое ядро, уменьшая количество листьев. Для сетей ErdoS-Renyi сетей, мы предполагаем, что 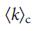= 2e = 5,436564, что согласуется с численными результатами (рис. 5 a, b), значение, которое совпадает
с 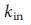где 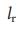достигает максимума. Действительно, 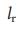начинает спадать при 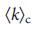, потому что для 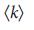> 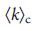число различных максимальных соответствий растет экспоненциально (раздел IV.C Дополнительной  Информации) и, как результат, вероятность того, что ссылка не участвует в любой конфигурации управления уменьшается. Для безмасштабных сетей, мы наблюдаем то же самое поведение, с оговоркой, что 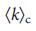уменьшается с 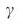(Рис. 5, c, d).

Обсуждение и выводы

Управление является одним из центральных вопросов в самых сложных системах, но из-за того что не хватает общей теории для исследования этих вопросов с применением количественных методов, нам мало известно о том, как мы можем контролировать взвешенные, ориентированные сети (конфигурации, которые наиболее часто встречаются в реальных системах). Действительно, применение условие ранга управляемости Калмана (уравнение (3)) для больших сетей чрезмерно с вычислительно точки зрения, ограничивая прменение предыдущих работ до сетей с количеством узлов не более нескольких десятков ^17-19. Здесь мы разработали инструменты для решения задачи по управлению сетью с произвольными топологией и размерами. Наш основной вывод о том, что 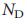определяется главным образом распределением степеней, позволяет нам использовать инструменты статистической физики, чтобы аналитически предсказать зависимость 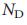от 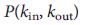, предлагая общий формализм для изучения влияния топологии сети на управляемость.

Рисунок 5 | Устойчивость управления. a,
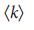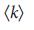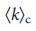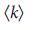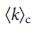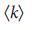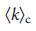
Зависимость доли критических (красные, LC), избыточных (зеленые, LR) и обычных (серые, LO) связей от для сетей Erdos–Renyi: lr достигает максимума при = = 2e, а производная LC терпит разрыв при = . b, Просачивание ядра для сетей Erdos–Renyi возникает при = = 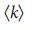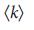2e, что объясняет пик LR. c, d, То же самое, что a и b, но для безмасштабных сетей. Сети Erdos–Renyi и безмасштабные сети³⁸ имеют N = 10⁴ и результаты усреднены для десяти реализаций с величиной ошибки, определенной как s.e.m. Пунктирные линиии обозначены лишь условно. e, Ядро (красные) и листья (зеленые) для малых сетей Erdos–Renyi networks (N = 30) с различными значениями ( = 4, 5, 7). Размер узла пропорционален степени узла. f, Критические (красные), избыточные (зеленые) и обычные (серые) связи поверх сетей Erdos–Renyi с соответствующими значениями .

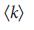Подход, представленный здесь вызывает ряд вопросов, ответы на которые могли бы еще больше углубить наше понимание задачи управления в сложных условиях. Например, несмотря на то, что наша аналитическая работа сосредоточена на некоррелированных сетях, алгоритмические методы, которые мы разработали, могут определить для произвольных сетей, обеспечивая систематизированную основу вопроса о роли корреляций ^{40, 49, 50}. Взятые вместе, наши результаты показывают, что при объединении инструментов науки о сетях и теории управления, многие аспекты управляемости могут быть изучены точно аналитическим способом для произвольных сетей, открывая новые пути для углубления нашего понимания сложных систем.

Дополнительная Информация к статье «Управляемость сложных сетей» доступна на сайте журнала Nature

Перевод подготовил Рабчевский Евгений.

1. Kalman, R. E. Mathematical description of linear dynamical systems. J. Soc. Indus. Appl. Math. Ser. A 1, 152–192 (1963).
2. Luenberger, D. G. Introduction to Dynamic Systems: Theory, Models, & Applications (Wiley, 1979).
3. Slotine, J.-J. & Li, W. Applied Nonlinear Control (Prentice-Hall, 1991).
4. Kelly, F. P., Maulloo, A. K. & Tan, D. K. H. Rate control for communication networks: shadow prices, proportional fairness and stability. J. Oper. Res. Soc. 49, 237–252 (1998).
5. Srikant, R. The Mathematics of Internet Congestion Control (Birkha¨user, 2004).
6. Chiang, M., Low, S. H., Calderbank, A. R. & Doyle, J. C. Layering as optimization decomposition: a mathematical theory of network architectures. Proc. IEEE 95, 255–312 (2007).
7. Wang, X. F. & Chen, G. Pinning control of scale-free dynamical networks. Physica A 310, 521–531 (2002).
8. Wang, W. & Slotine, J.-J. E. On partial contraction analysis for coupled nonlinear oscillators. Biol. Cybern. 92, 38–53 (2005).
9. Sorrentino, F., di Bernardo, M., Garofalo, F. & Chen, G. Controllability of complex networks via pinning. Phys. Rev. E 75, 046103 (2007).
10. Yu, W., Chen, G. & Lu¨, J. On pinning synchronization of complex dynamical networks. Automatica 45, 429–435 (2009).
11. Marucci, L. et al. Howto turn a genetic circuit into a synthetic tunable oscillator, or a bistable switch. PLoS ONE 4, e8083 (2009).
12. Strogatz, S. H. Exploring complex networks. Nature 410, 268–276 (2001).
13. Dorogovtsev, S. N. & Mendes, J. F. F. Evolution of Networks: From Biological Nets to the Internet and WWW (Oxford Univ. Press, 2003).
14. Newman, M., Baraba´si, A.-L. & Watts, D. J. The Structure and Dynamics of Networks (Princeton Univ. Press, 2006).
15. Caldarelli, G. Scale-Free Networks: Complex Webs in Nature and Technology (Oxford Univ. Press, 2007).
16. Albert, R. & Baraba´si, A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47–97 (2002).
17. Tanner, H. G. in Proc. 43rd IEEE Conf. Decision Contr. Vol. 3, 2467–2472 (2004).
18. Lombardi, A. & Ho¨ rnquist, M. Controllability analysis of networks. Phys. Rev. E 75, 56110 (2007).
19. Liu, B., Chu, T., Wang, L. & Xie, G. Controllability of a leader–follower dynamic network with switching topology. IEEE Trans. Automat. Contr. 53, 1009–1013 (2008).
20. Rahmani, A., Ji, M., Mesbahi, M. & Egerstedt, M. Controllability of multi-agent systems from a graph-theoretic perspective. SIAM J. Contr. Optim. 48, 162–186 (2009).
21. Kim, D.-H.&Motter, A. E. Slave nodes and the controllability ofmetabolic networks. N. J. Phys. 11, 113047 (2009).
22. Mesbahi, M. & Egerstedt, M. Graph Theoretic Methods in Multiagent Networks (Princeton Univ. Press, 2010).
23. Motter, A. E., Gulbahce, N., Almaas, E.&Baraba´si, A.-L. Predicting synthetic rescues in metabolic networks. Mol. Syst. Biol. 4, 168 (2008).
24. Pastor-Satorras, R. & Vespignani, A. Evolution and Structure of the Internet: A Statistical Physics Approach (Cambridge Univ. Press, 2004).
25. Lezon, T. R., Banavar, J. R., Cieplak, M., Maritan, A. & Fedoroff, N. V. Using the principle of entropy maximization to infer genetic interaction networks from gene expression patterns. Proc. Natl Acad. Sci. USA 103, 19033–19038 (2006).
26. Lin, C.-T. Structural controllability. IEEE Trans. Automat. Contr.19, 201–208(1974).
27. Shields, R. W. & Pearson, J. B. Structural controllability of multi-input linear systems. IEEE Trans. Automat. Contr. 21, 203–212 (1976).
28. Lohmiller, W. & Slotine, J.-J. E. On contraction analysis for nonlinear systems. Automatica 34, 683–696 (1998).
29. Yu, W., Chen, G., Cao, M. & Kurths, J. Second-order consensus for multiagent systems with directed topologies and nonlinear dynamics. IEEE Trans. Syst. Man Cybern. B 40, 881–891 (2010).
30. Hopcroft, J. E.& Karp, R. M. An n5/2 algorithmfor maximummatchings in bipartite graphs. SIAM J. Comput. 2, 225–231 (1973).
31. Albert, R., Jeong, H. & Baraba´si, A.-L. Error and attack tolerance of complex
networks. Nature 406, 378–382 (2000).
32. Cohen, R., Erez, K., Ben-Avraham, D. & Havlin, S. Resilience of the Internet to random breakdowns. Phys. Rev. Lett. 85, 4626–4628 (2000).
33. Pastor-Satorras, R. & Vespignani, A. Epidemic spreading in scale-free networks. Phys. Rev. Lett. 86, 3200–3203 (2001).
34. Nishikawa, T., Motter, A. E., Lai, Y.-C. & Hoppensteadt, F. C. Heterogeneity in oscillator networks: are smaller worlds easier to synchronize? Phys. Rev. Lett. 91, 014101 (2003).
35. Erdo˝s, P. & Re´nyi, A. On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci. 5, 17–60 (1960).
36. Bolloba´s, B. Random Graphs (Cambridge Univ. Press, 2001).
37. Baraba´si, A.-L.&Albert, R.Emergence of scaling in randomnetworks. Science 286, 509–512 (1999).
38. Goh, K.-I., Kahng, B. & Kim, D. Universal behavior of load distribution in scale-free networks. Phys. Rev. Lett. 87, 278701 (2001).
39. Chung, F. & Lu, L. Connected component in random graphs with given expected degree sequences. Ann. Combin. 6, 125–145 (2002).
40. Maslov, S. & Sneppen, K. Specificity and stability in topology of protein networks. Science 296, 910–913 (2002).
41. Milo, R. et al. Network motifs: simple building blocks of complex networks. Science 298, 824–827 (2002).
42. Me´zard, M. & Parisi, G. The Bethe lattice spin glass revisited. Eur. Phys. J. B 20, 217–233 (2001).
43. Zdeborova´, L. & Me´zard, M. The number of matchings in random graphs. J. Stat. Mech. 05, 05003 (2006).
44. Zhou, H. & Ou-Yang, Z.-c. Maximum matching on random graphs. Preprint at Æhttp://arxiv.org/abs/cond-mat/0309348æ (2003).
45. Callaway, D. S., Newman, M. E. J., Strogatz, S. H. & Watts, D. J. Network robustness and fragility: percolation on random graphs. Phys. Rev. Lett. 85, 5468–5471 (2000).
46. Bogun˜a´, M., Pastor-Satorras, R. & Vespignani, A. Cut-offs and finite size effects in scale-free networks. Eur. Phys. J. B 38, 205–209 (2004).
47. Lova´sz, L. & Plummer, M. D. Matching Theory (American Mathematical Society, 2009).
48. Bauer, M. & Golinelli, O. Core percolation in random graphs: a critical phenomena analysis. Eur. Phys. J. B 24, 339–352 (2001).
49. Newman,M.E. J.Assortativemixinginnetworks.Phys.Rev.Lett.89,208701(2002).
50. Pastor-Satorras, R., Va´zquez, A. & Vespignani, A. Dynamical and correlation properties of the Internet. Phys. Rev. Lett. 87, 258701 (2001).

Автор: rabchevsky

Источник