В современном мире отношения между людьми помимо социального уровня заняли еще один — цифровой. С распространением виртуальных социальных сетей появилась тенденция иметь собственную страницу с персональными данными, искать друзей по интересам, создавать группы и пр. Количество информации в соцсетях постоянно увеличивается. Возникла мысль обработать данные, которые, на первый взгляд, не кажутся полезными, но после обработки вполне могут послужить на благое дело.
В данной статье рассматривается поиск наиболее влиятельных объектов. Данная информация может быть полезна как для проведения различных виртуальных маркетинговых акций, так и для выявления пользователей с подозрительно высокой активностью.
Введение
Будем обозначать социальную сеть в виде графа, узлами которого являются люди. Если объекты как-то связаны между собой (состоят в друзьях, либо переписываются), то между этими объектами есть дуга.
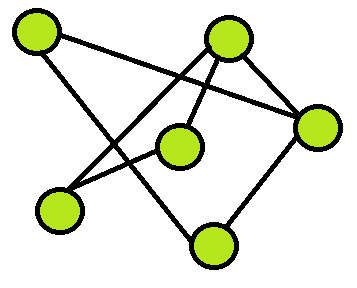Рис. 1
Дадим интуитивное понятие влиятельности. Рассмотрим следующий рисунок.
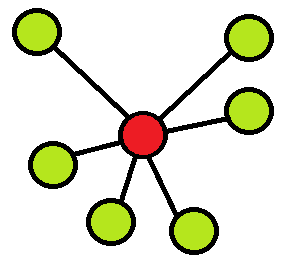Рис. 2
Тут объект в центре имеет 6 связей. Но влиятельность не сводится только к количеству связей. Мы должны учесть степень влияния объектов, с которыми связан целевой объект. Рассмотрим рис. 3.
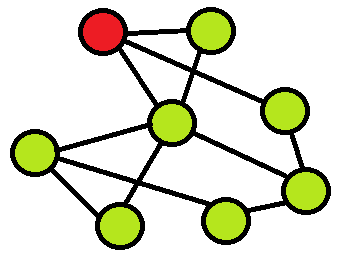Рис. 3
На вышеуказанном рисунке видно, что объект имеет 3 связи, но объекты, с которыми он связан, обладают некоторым влиянии в сети. Нужно таким образом формализовать понятие влиятельности, чтобы учитывались как количество связей, так и влиятельность объектов, с которыми связан целевой объект.
Матчасть
Толчком для исследования в этом направлении стала данная статья[1]. Я внес в предложенный алгоритм поправки, которые на мой взгляд кажутся целесообразными.
Граф будем представлять в виде матрицы смежности.
Введем понятие итерированной силы объекта i порядка k.
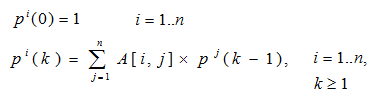
Заметим, что итерированная сила первого порядка объекта i есть количество связей данного объекта с другими. Она пока что еще не учитывает влиятельность других объектов. Начиная со второго порядка в данную сумму включается влиятельность иных объектов.
Вопрос: до какого порядка считать вектор итерированных сил?
Ответ: либо 2, либо 3.
Дело в том, что итерированная сила объекта i порядка k выражает степень влияния объекта i, учитывая, что он свое влияние может распространить не более чем в радиусе k. Так заложено в самой сумме. Вспомните когда вы просили своего друга, чтобы он попросил кого-то сделать что-то для вас? Это влиятельность в радиусе 2, и выражается она итерированной силой второго порядка. Если мы хотим учитывать цепи с еще одним промежуточным участником, то нужно считать вектор итерированных сил 3-го порядка. Считать итерированные силы бОльших порядком кажется нецелесообразным ввиду ничтожно малой вероятности возникновения столь длинных цепочек в реальной жизни.
Таким образом, если мы хотим посчитать влиятельность объектов в масштабе крупного города и выше, то считаем до 3-го порядка. Для меньших масштабов целесообразно использовать второй порядок.
Заметим, что нам важно не численное значение итерированной силы, а то, как силы для разных объектов соотносятся между собой. Поэтому после расчета вектора итерированной силы очередного порядка целесообразным будет нормировать данный вектор. В качестве нормы берется максимум по абсолютным значениям его элементов.
Собираем информацию
Информация собиралась из социальной сети «Вконтакте». Было написано приложение, которое загружает 2 набора друзей: до 2-го и до 3-го уровней. Для большей ясности рассмотрим рисунок 4.
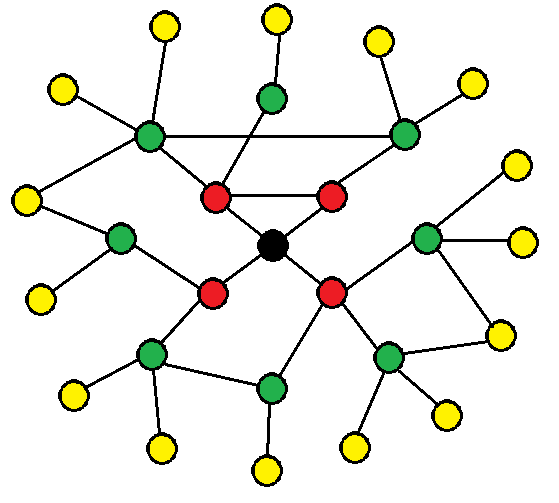Рис. 4
Здесь красным обозначены друзья 1-го уровня, зеленым – второго, желтым – третьего. В силу того, что VK API не позволяет делать более 3 запросов в секунду, то для загрузки третьего уровня приходилось оставлять машину включенной на ночь.
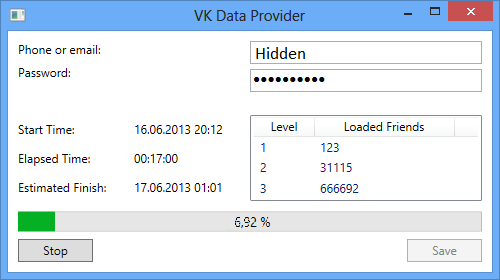Рис. 5
Заметим, что если загружать 4 уровня, то скорее всего мы скачаем 99 % пользователей сети. Существует теория шести рукопожатий [2], которая утверждает, что между любыми двумя людьми на Земле не более 5 уровней общих знакомых. В силу того, что VK распространена в основном в СНГ, то эта цифра должна быть меньшей.
Анализируем данные
Итак, у нас есть 2 набора данных:
- Для 2 уровней друзей – примерно 40 тыс. пользователей.
- Для 3 уровней друзей – примерно 4,2 млн. пользователей.
Я сам в соцсетях не сижу, поэтому в обоих случаях центром выборки был мой друг, студент Воронежского ГосУниверситета.
Начнем с анализа первого набора.
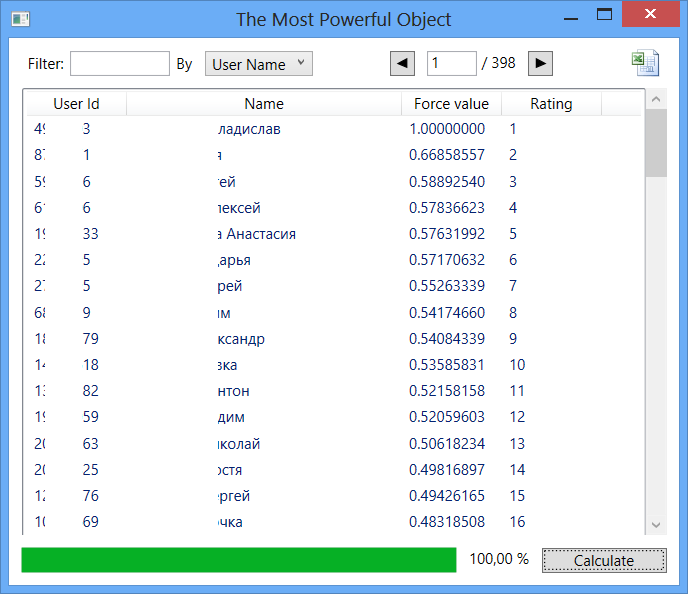Рис. 6
Здесь центр выборки занял первое место по влиятельности. Объяснить это можно тем, как загружались данные. Дело в том, что весь последний уровень друзей содержит лишь по одной связи. Для этих объектов список друзей пуст. Поэтому влиятельность друзей 1-го уровня (которая в значительной степени базируется на друзьях 2-го уровня) оценивается низко. Из-за этого мы получаем не совсем объективные результаты. Тем не менее, можно наблюдать интересные данные: в первых 30 строках располагаются около половины активистов ВГУ.
Перейдем к исследованию второго набора данных. Здесь центр выборки по рейтингу занимает 3539 место.
Оно и понятно: тут уже влиятельность рассматривается в рамках города.
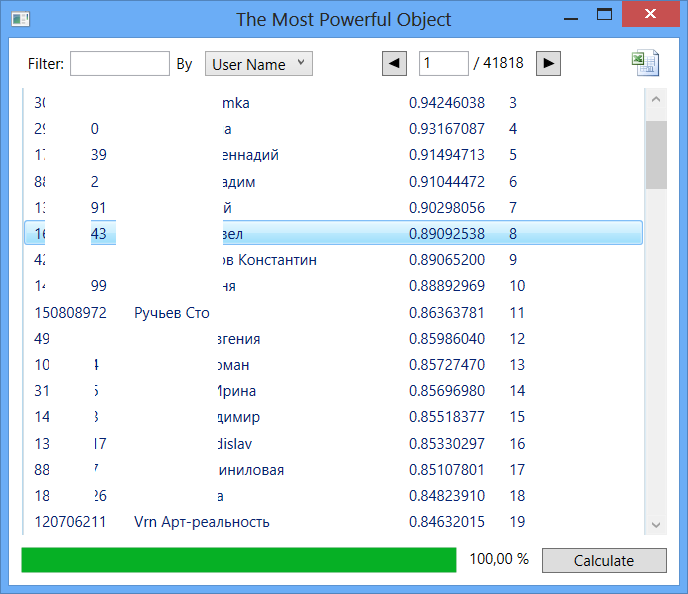Рис. 7
В начале данной таблицы прослеживаются следующие записи:
- Воронеж Афиша
- Врн экскурсии
- Воронеж nightparty.ru
- Ручьев Сто
- Арт-реальность Vrn
Что касается людей в первых строчках данного списка, можно сказать, что часть из них действительно известные люди (в основном фотографы) нашего города. Но активность некоторых объектов вызывает подозрение: слишком большая степень влияния при достаточно скупой информации о личности. Данные объекты могут быть рассмотрены администраторами сети на соответствие информации действительности.
P.S. Если у кого есть мысли как можно улучшить данную модель, прошу отписаться в комментариях.
Источники:
- www.basegroup.ru/library/web_mining//information_flows_in_social_networks/
- ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D1%88%D0%B5%D1%81%D1%82%D0%B8_%D1%80%D1%83%D0%BA%D0%BE%D0%BF%D0%BE%D0%B6%D0%B0%D1%82%D0%B8%D0%B9
Автор: RusProg
