Упрощать сложно. История одного провала

В работе мне часто (да что там часто, практически всегда) приходится иметь дело с численным моделированием газодинамики (реже - МГД), как правило, трехмерным и, что важно, весьма масштабным по вычислительным затратам. Рассказывать про численные модели можно долго, но в данной статье это будет излишним, так что попробую изложить их суть в нескольких словах. Итак, представьте себе область пространства, заполненную газом. Где-то в нем находится пара звезд, создающих гравитационное поле, а также, (обычно) одна из них служит источником газа, теряя его с поверхности, например, в виде ветра. Мы разбиваем пространство на ячейки, обычно прямоугольные, которые достаточно малы, чтобы считать параметры газа (плотность, скорость, температуру) в них постоянными. Далее, мы разбиваем время на отрезки (шаги), тоже достаточно мелкие, чтобы за время одного шага в системе мало что менялось. А потом начинаются вычисления - зная параметры газа в двух соседних ячейках мы можем, используя сложные системы уравнений, вычислить поток между ними и определить, как параметры газа в них должны измениться за время одного шага. Зная это, мы обновляем значения в ячейках и переходим к следующему временному шагу, а потом еще и еще. В итоге получается что-то вроде этого:

Чтобы всё хорошо работало, ячеек должно быть много, а временные шаги короткими. Чем больше и чем короче, тем выше точность и более тонкие эффекты можно поймать. Уже 20 лет назад наши модели стали настолько тяжелыми, что от вычислений на персоналках мы перешли к суперкомпьютерам, а сейчас нам не хватает и их. Так что вопросы оптимизации кодов, которыми мы пользуемся, стоят очень остро. Выигрыш даже нескольких процентов скорости может сэкономить дни вычислений с использованием сотен процессорных ядер. И я в какой-то момент подумал: а почему бы не автоматизировать написание численных кодов?

Попытка первая

Казалось бы, отличная идея. Мы берем систему уравнений, берем численную схему, соединяем одно с другим (на практике это выглядит как перемножение матриц и векторов), задаем параметры сетки, метод параллелизации, начальные и граничные условия, нажимаем на кнопку и компьютер нам выдает готовый код, оптимальный и распараллеленный, остается только запустить его. Что тут может пойти не так?!

Маленькое отступление. Хотя программирование и не моя специальность, программирую я довольно много. То, что результатом моей работы является не программа, а ее вывод, позволяет мне свободно использовать инструменты, за одно упоминание которых в приличных организациях бьют по голове. Так что к тому моменту я уже писал что-нибудь полезное примерно на 15 разных языках программирования, а также успел "потрогать руками" еще с десяток. И когда мне захотелось побаловаться символьной математикой, я, нисколько не смущаясь, выбрал для этого самый подходящий лисп-подобный язык - Scheme. Синтаксис "со скобочками" оказался невероятно удобен для представления формул, их легко было обрабатывать и вообще, сам язык мне нравился.

В общем, довольно быстро я забил в него необходимые формулы, схемы Роу и Ошера, энтропийную поправку Эйнфельдта, написал набор простых функций для перемножения всяких векторов и матриц, придумал забавный способ для избежания ветвлений, запустил, и... для трехмерной схемы идеальной газодинамики получил уравнения эпических размеров. Некоторые имели более 100 тыс. членов. Это меня озадачило. Внимательный осмотр показал, что уравнения имеют, так сказать, потенциал к упрощению. Весьма немалые их куски умножались на ноль, например. А другие части можно было бы и сократить между собой. Надо упрощать, подумал я.

Сначала я пошел по легкому пути. Установил maxima - систему компьютерной алгебры, которой в автоматическом режиме передавал выражения для упрощения. Но результат меня не удовлетворил. Во-первых, она работала очень медленно, во вторых я глазами видел, как можно полученные уравнения упростить еще сильнее. И я отважно взялся писать код, который будет упрощать выражения так, как мне хотелось бы.

Итак, что мы имеем? У нас есть выражения, записанные в характерной для лисп префиксной нотации. Например, выражение:

будет записано как:

'(sqrt (+ A (* B (+ C D))))

Для тех, кому лисп не близок, поясню немного смысл выражения. Скобки ограничивают список из элементов, которые тоже могут быть списками. Элементы разделены пробелами. A, B, C, D и sqrt - т.н. символы, то есть некие уникальные сущности, имеющие имена. Больше того, + и * это тоже символы. В принципе, элементом списка может быть что угодно, но для простоты будем считать, что в наших списках будут только символы и числа.

Такой способ записи выражений имеет большое преимущество. Во-первых, лисп создан для работы со списками и если наше выражение это список, то им можно удобно манипулировать. Во-вторых, эти списки имеют единый формат. Например, в C выражения бывают вида cos(x), то есть имя функции и параметры в скобках, перечисляемые через запятую, а также вида a+b-c+d когда операторы разделяют операнды. Один разбор этого выражения (а ведь в нем тоже могут быть скобки! И некоторые из них, но не все, ограничивают параметры функций!) может стать темой дипломной работы, чего уж тут говорить об удобстве. В лисп же первый член списка это всегда обозначение функции, а все остальные - ее параметры. В общем, если вам нужно работать с символьными выражениями, выбирайте лисп, не пожалеете.

Итак, у нас есть выражения в виде списков, пора подумать, как их упрощать. Для начала я решил избавиться от вычитаний и делений. Они мне не нравились с детства. Действительно, зачем вычитать и делить, когда можно складывать и умножать?! А если серьезно, то эти функции могут иметь произвольное (>1) число параметров, которые можно менять местами, но кроме первого. Неаккуратненько. Избавиться от них довольно просто, действительно:

Легким движением руки вычитания превращаются в сложения, а деления в умножения!

Дальше я пошел немного неверным, как в последствии оказалось, путем. Я решил еще более унифицировать выражения, оставив в них максимум два операнда. То есть произвести преобразования вида:

Мне показалось это хорошей идеей. Действительно, если у нас до этого был список списков, то есть дерево, то почему бы не превратить его в двоичное дерево, наиболее простую и естественную форму? А дальше, по моему замыслу, я бы писал шаблоны вида:

которые бы применял рекурсивно до тех пор, пока не останется ни одного шаблона, которое можно было бы применить. Рекурсия, чтобы вы знали, это не менее характерная фишка лисп, чем списки. Говорим лисп - подразумеваем рекурсию! В общем, я создал простые функции для поиска и замены шаблонов и начал эти самые шаблоны писать. Я смотрел глазами на выражения, находил в них кусок, который можно упростить и добавлял соответствующий шаблон. Запускал, получал новое выражение, снова смотрел на него и так далее. Я был упорен и верил в себя. Результат выглядел примерно так:

Слабонервным не смотреть!

В целом, всё шло неплохо. В местах, где просто шаблонов было недостаточно, я вставлял костыли в виде кода. Лисп изначально разрабатывался как язык для написания искусственного интеллекта, причем в те времена считалось, что ИИ будет строго алгоритмическим, просто алгоритм будет очень сложным. И лисп хорошо приспособлен для сложных алгоритмов, включающих неограниченное количество костылей. Мне это очень подходило! Но чем больше шаблонов я писал, тем менее предсказуемым становилась поведение программы. Иногда добавление довольно невинного шаблона приводило к многократному увеличению времени работы или к резкому росту потребления памяти, причем не факт, что выражения становились проще после этого, зачастую происходило обратное. В целом, мне удалось добиться более-менее удовлетворительных результатов, сгенерировать оптимизированный параллельный код (даже для GPU!) и посчитать несколько тестовых задач, вполне успешно. Вот, например, холодная сверхзвуковая затопленная струя в 2D:

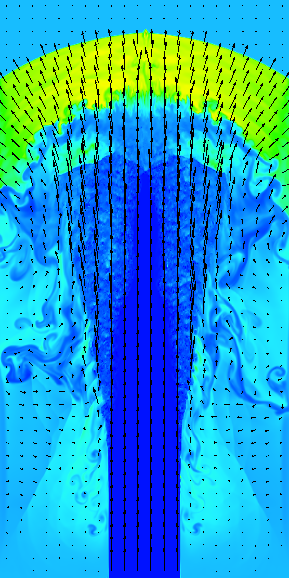
Но, глобально, конечно, это был провал. Упрощение выражений оказалось задачей гораздо более сложной, чем мне виделось. Проект я забросил, но не забыл.

Попытка вторая

Прошло несколько лет. Все эти годы меня глодал червячок неудовлетворенности. Ведь подкосила меня проблема, которая казалась пустяковой - сокращение членов в выражении. Да третьеклассники легко справляются с этой задачей! В общем, в какой-то момент терпение мое лопнуло и я снова взялся за лисп.

На этот раз я решил писать код не на Scheme, а на Common Lisp (CL). Основная причина - для CL есть хорошие компиляторы. Да, компиляторы Scheme тоже есть, но мне не удалось найти такого, который был бы а) кросплатформенным, б) хорошо оптимизирующим и в) бесплатным. А для CL, который является прямым потомком того самого лиспа, есть отличные кроссплатформенные компиляторы, из которых наиболее распространен SBCL.

Окунувшись в разнузаднный и анархичный Common Lisp после лаконичного и академичного Scheme, я чувствовал себя как выпускник консерватории, впервые попавший на рок-концерт. Отдельную роль тут сыграла книжка Common Lisp Recepies, которую можно сравнить только с книгой по черной магии, после книги по белой магии SICP. По началу мне многое в этом языке казалось лишним, ненужным, неуклюжим и громоздким. Однако, через некоторое время, я, так сказать, втянулся и обнаружил, что за более чем полувековую историю этот язык приобрел, даже не знаю, как сказать, завершенность, что ли? На все грабли, на которые можно наступить в нем уже кто-то наступил до тебя, наступил столько раз, что даже в стандарт языка уже добавлены специальные мягкие резиновые накладки для черенков. И это как раз те вещи, которые показались мне странными и излишними при первом знакомстве с CL, но очень пригодились впоследствии. В общем, не буду скрывать, я влюбился в лисп во второй раз. Что забавно, в отличие от Scheme, которая считается ветвью Lisp-1, CL это, вы не поверите, как раз Lisp-2.

Итак, я начал с чистого листа, вооруженный бесценным опытом, полученным во время первой попытки. Сначала произвожу все матричные и векторные операции, так, чтобы получить результирующую матрицу или вектор, с элементами которых можно работать независимо. Потом, конечно, избавляюсь от вычитаний и делений, как было показано выше. А дальше начинается вся подкапотная магия.

Я решил, что на первом этапе надо вычислять в выражении всё, что можно вычислить. То есть, если у нас есть выражение

мы должны превратить его в

сложив числа, а также выкинув всё, что умножается на 0, выкинуть 1 там, где происходит умножение на 1 и т.д. Назовем эту процедуру extract-nums. Как оказалось впоследствии, это самая важная процедура во всем упрощении, по сути, упрощение происходит именно в ней, а остальное это так, преобразование выражений, чтобы extract-nums мог выкинуть ненужное.

Далее, если вы помните, я преобразовывал всё к виду двоичного дерева, но на этот раз решил пойти диаметрально противоположным путем - я собираю однотипные операции, раскрывая скобки:

Затем, раскрываю скобки в возведении в степень:

Логарифмы тоже разбираю на части:

для логарифмов там еще есть несколько преобразований, полезных, в основном, при дифференцировании, но об этом позже.

А затем, парадоксальным образом, я снова собираю выражения под скобки:

...и снова прогоняю extract-nums! Казалось бы, где тут логика? А логика вот она:

Это упрощенный пример, не требующий раскрытия скобок, но показывающий, как происходит сокращение множителей в числителе и знаменателе. Заметьте, у нас выпало только на последних этапах, в extract-nums!

А потом я... снова раскрываю скобки! Но на этот раз в умножениях:

и опять extract-nums, чтобы выкинуть лишнее. После чего, начинает работу самая сложная и попившая мне крови функция, которая выносит за скобки общие члены:

и потом, опять же, extract-nums сокращает члены в сложениях. Казалось бы, что тут сложного? А вот что:

Заметьте, что тут встречается как выражение в скобках и как часть суммы . То есть просто сравнением выражений при поиске общих членов мы не обойдемся, нужно еще искать подвыражения внутри сумм. Но это еще цветочки, а вот ягодки:

Тут встречается как , так что нам нужно не просто искать подвыражения, но и еще их же, умноженные на -1. Бывает и хуже:

В общем, вынесение за скобки это боль. Примерно 80% времени отладки ушло на этот кусок. Чтобы масштаб был вам понятен, уточню, что процедура, вдобавок, рекурсивная, выносящая за скобки более чем одно подвыражение, но это не та рекурсия, которая используется в остальных местах, где нам нужно просто пройти по дереву, нет, тут мы сначала проходим по дереву, потом рекурсивно выносим за скобки выражения в корне дерева, причем это может быть частью предыдущей рекурсии. Но даже это мне удалось отладить. Еще одна причина любить лисп и функциональное программирование.

Вынос общих переменных, это как переход через экватор. До него мы как бы разбирали выражение на части, а начиная с него (ну, чуть раньше на самом деле, но не суть) уже собираем обратно. Например:

Это делается не только для красоты, но также может считаться упрощением, поскольку уменьшает количество операций. А затем... повторяем всё сначала. Снова разбираем выражения, снова выносим всё за скобки, снова extract-nums нам всё сокращает... И так, пока выражение не перестанет изменяться. А потом уже занимаемся украшательством. Возвращаем вычитания и деления, превращаем в и т.д. Всё, мы упростили. Готово.

Библиотечку symath, которая делает всё это и кое-что другое, я выложил здесь, лицензия MIT. Использовать с осторожностью!

Стоп! А как же...

А как же, например, тригонометрия? Как же известное со школы равенство:

Неужели его не получится учесть? Всё же подход с деревьями и шаблонами был в чем-то гибче... Всем сохранять спокойствие! Шаблоны уже тут! Но я немного изменил к ним подход. И пока они используются только для дифференцирования.

Как говорил мой преподаватель в университете, дифференцировать можно научить и обезьяну. Правил немного и они простые. И сам бог велел использовать для этого шаблоны и на этот раз мои шаблоны выглядят так:

(diff @ $) => 0)
(diff _1 _1) => 1)
(diff (exp $1) _2) => `(* (exp ,$1) (diff ,$1 ,_2))

Или даже вот так:

(diff (+ &rest args) _1) =>
  (cons '+ (mapcar (compose (curry #'cons 'diff) (rcurry #'list _1)) args))))

Не пугайтесь, это тоже лисп. В нем можно придумать себе удобный синтаксис, средствами языка реализовать его и потом писать так код. Для шаблонов я придумал следующие обозначения:

• @ - это константа, причем не обязательно число (см. ниже)

• $ - это что угодно, но не константа

• _ - вообще что угодно!

• => - разделяет шаблон и замену. Пока ставится только для красоты, но потом я добавлю другие разделители и они будут иметь смысл (см. ниже)

• &rest var - поместить все остальные члены выражения списком в переменную var

• @1, $X, _Y - поместить то, что в шаблоне, в переменные. Да, так можно назвать переменные в лиспе, это нормально.

• Всё, что после => - код, который должен вернуть выражение, заменяющее шаблон, либо NIL, если шаблон заменять не надо.

• mapcar, cons, compose, curry и пр. - местные идеоматические выражения.

Теперь должно быть понятно, что означают шаблоны:

(diff @ $) => 0) ;; Производная от константы всегда 0
(diff _1 _1) => 1) ;; Производная от X по X всегда 1
(diff (exp $1) _2) => 
  `(* (exp ,$1) (diff ,$1 ,_2)) ;; Производная от экспоненты - см. шпору по алгебе

Код во второй части шаблона зачастую тоже похож на какой-то шаблон. Это неспроста - в лиспе данные это тоже код. То есть 0 это код, который возвращает 0, очень удобно. Шаблоны применяются рекурсивно до тех пор, пока не останется ни одного, который можно было бы применить, после чего происходит уже обычное упрощение, описанное выше. Так что, чтобы продифференцировать выражение, нужно просто поместить его под функцию , вторым параметром которой будет переменная, по которой дифференцируем, после чего вызвать функцию simplify:

(simplify '(diff (exp (cos x)) x))
  => (* -1 (EXP (COS X)) (SIN X))

Если для дифференцирования какой-нибудь экзотической функции нет подходящего шаблона, она так и останется под :

(simplify '(diff (exp (foo x)) x))
  => (* (EXP (FOO X)) (DIFF (FOO X) X))

Но можно добавить свой шаблон для этой функции, через макрос with-templates:

(with-templates (((diff (foo $1) $2) =>
                    `(/ (- (foo ,(replace-subexpr $1 $2 `(+ ,$2 delta)))
                           (foo ,(replace-subexpr $1 $2 `(- ,$2 delta))))
                        (* 2 delta))))
    (simplify '(diff (exp (foo x)) x) :no-cache t))
  => (/ (* (- (* 1/2 (FOO (+ X DELTA))) (* 1/2 (FOO (- X DELTA)))) (EXP (FOO X)))
     DELTA)

Тут мы заменяем производную от функции foo на центральную конечно-разностную производную, используя функцию replace-subexpr из той же библиотечки symath. Кстати, зацените, в лиспе есть тип rational - 1/2 это не 0.5!

Иногда нам может быть полезно объявить какое-либо выражение константой. Чтобы, например, вместо:

(simplify '(diff (expt x y) x)) ;; дифференцируем функцию X^Y по X
  => (* (+ (* (DIFF Y X) (LOG X)) (/ Y X)) (EXPT X Y)) ;; Тут неизвестный нам дифференциал dY/dX

получить:

(with-constants (y) (simplify '(diff (expt x y) x) :no-cache t))
  => (* Y (EXPT X (- Y 1)))

используется макрос with-constants, чтобы simplify знал, что y это константа. Заметьте, что закон понижения степени при дифференцировании явно не задан, он получается сам собой, если знать, что !

Дифференцирование, кстати, оказалось не такой уж и простой операцией. Мне недавно потребовалось (не спрашивайте) разложить в ряд Тейлора по двум переменным функцию, в которой было несколько членов вида:

Уже для взятия пятой производной потребовалось несколько часов и пара гигабайт памяти.

В дальнейшем я хочу расширить использование шаблонов, чтобы с их помощью можно было не только дифференцировать, но и вводить новые правила упрощения, например, тригонометрические. Как вариант, можно применять шаблоны при сравнении выражений.

Второй по значимости, после extract-nums, в symath является функция (equal-expr e1 e2), которая определяет, являются ли выражения e1 и e2 одним и тем же выражением. Функция не совсем проста, она может определить, что суммы с разным порядком членов, например, эквивалентны. Еще более сложная функция (equal-expr1 e1 e2), которая проверяет, является ли e1 эквивалентом -e2. Можно усложнить их еще больше, добавив сравнение с учетом шаблонов, чтобы, например, было эквивалентно и наоборот. Это будет работать при вынесении общих множителей и при сокращении числителей со знаменателями. Плюс, в конце, где мы собираем выражение обратно, можно будет делать замены для тех шаблонов, которые уменьшают число операций. Поскольку такие шаблоны будут обратимы, в них нельзя будет использовать код для вычисления замены, так что нужно будет их обозначать особо. Например, вместо разделителя => ставить <=>.

Так, что там еще?

В symath есть еще немного полезных функций. Одна из них, replace-subexpr, уже засветилась выше - она нужна для замены одного подвыражения на другое, просто рекурсивно проходит дерево и заменяет всё, что эквивалентно с точки зрения equal-expr.

Функция extract-subexpr более интересна. Она позволяет "изолировать" некое выражение, то есть привести исходную формулу к виду:

где - искомое выражение, а , и - выражения, которые в явном виде не содержат . Как нетрудно догадаться, при помощи этой функции можно находить тривиальные решения некоторых простых уравнений. Но всё же на полноценный решатель она не тянет, потому мне не хватило наглости назвать ее solve.

Вызывая эту функцию рекурсивно, можно представить выражение в виде полинома относительно . Что и делает функция get-polynome-cfs, возвращающая коэффициенты полинома в виде ассоциативного списка. Мне эта функция понадобилась, когда нужно было найти область пересечения конуса с плоскостью, я рассчитывал коэффициент затенения звезды экзопланетой для ячеек в счетной области. Я выполнил преобразования векторов, получив некое (довольно внушительных размеров) уравнение, которое привел с помощью этой функции к квадратному и, записав дискриминант, получил критерий.

Итоговое уравнение тоже получилось эпическим, даже после упрощения, но его удалось привести к более компактной форме, при помощи функции split-to-subexprs. Эта функция, как нетрудно догадаться, выносит из выражения наиболее часто встречающиеся куски в отдельные переменные. (Ахтунг! Буквально недавно я обнаружил, что она багованная! Еще не исправлено.)

Еще одна полезная штука, для которой в библиотеке нет явной функции - проверка выражений на эквивалентность, более надежная, чем банальный equal-expr. Чтобы проверить, эквивалентны ли выражения и , нужно просто упростить левые части следующих выражений и проверить их истинность:

Если хотя бы в одном случае получается или , выражения эквивалентны. Почему стоит проверять два варианта? Библиотека, увы, не всесильна и пока еще недостаточно совершенна, чтобы полностью всё сократить в обоих случаях. Но я работаю над этим!

Вместо заключения

Честно говоря, я не думал, что найдется достаточно желающих пользоваться этой библиотечкой. Как минимум, лисп не настолько популярен, мне кажется. Однако, статистика гитхаба показывает, что в этот репозиторий постоянно приходят какие-то люди из поиска гугла и ежедневно несколько раз его кто-то клонирует (с десяток уникальных клонеров за неделю!). У меня серьезные подозрения, что люди ищут что-то другое, с похожим названием. Если кто-то из читающих эту статью знает, что именно им нужно - напишите в комментариях! Очень любопытно будет узнать :)