На сегодняшний день случайность повсеместно используется в нашей жизни. Она есть в научных работах и исследовательских моделях, защитных алгоритмах и криптосистемах, в лотереях и азартных играх, системах автоматизации и математике. Сейчас я немного расскажу про ГСЧ и какие плюсы и минусы можно от них получить в той или иной сфере.
Как мы получаем последовательности случайных чисел?
Как уже было сказано выше, современный мир довольно сильно зависит от случайных чисел и нам необходимо как-то их получать. И сейчас мы имеем два способа генерации случайных последовательностей.
-
Генератор истинно случайных чисел
Аппара́тный генера́тор случа́йных чи́сел (генератор истинно случайных чисел) — устройство, которое генерирует последовательность случайных чисел на основе измеряемых, хаотически изменяющихся параметров протекающего физического процесса.
Думаю, что данный вид генераторов является своего образа эталоном для получения случайных последовательностей, так как в своей работе они используют различные надежные источники энтропии. Но с другой стороны ГИСЧ имеют ряд недостатков: они громоздкие, дорогие в создании и настройке, а также медленнее программных алгоритмов.
-
Генераторы псевдослучайных чисел
Генератор псевдослучайных чисел (ГПСЧ, англ. pseudorandom number generator, PRNG) — алгоритм, порождающий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному).
Наиболее распространенный тип генераторов в реальном мире. Они проще и дешевле, но имеют изъян в своей "псевдослучайности". Так что с развитием технологий человечеству приходится создавать новые ГПСЧ, которые защищены вычислительно сложной задачей от взлома машиной.
ГПСЧ
Конечно, как и любая технология, ГПСЧ должен обладать какими-то качествами. Согласно статье на Википедии, имеется 4 критерия:
-
Достаточно длинный период, гарантирующий отсутствие зацикливания последовательности в пределах решаемой задачи. Длина периода должна быть математически доказана;
-
Эффективность — быстрота работы алгоритма и малые затраты памяти;
-
Воспроизводимость — возможность заново воспроизвести ранее сгенерированную последовательность чисел любое количество раз;
-
Портируемость — одинаковое функционирование на различном оборудовании и операционных системах;
-
Быстрота получения
элемента последовательности чисел, при задании 
элемента, для 
любой величины; это позволяет разделять последовательность на несколько потоков (последовательностей чисел).
Стандарты ГПСЧ
На сегодняшний момент существует множество документов, которые регламентируют, каким должен быть хороший ГПСЧ. Приведу несколько примеров:
-
ГОСТ Р 34. 11-2012, ГОСТ Р ИСО 28640-2012 - в данных стандартах описаны функция хеширования, которую можно применить как часть ГПСЧ, а также стандарт создания случайных чисел для применения их в методе Монте-Карло.
-
ANSI X9.82 - описание и базовые принципы ГПСЧ
-
NIST SP 800-22 - в данной публикации приведен набор тестов для ГСЧ и ГПСЧ
Одним из первых ГПСЧ был линейный конгруэнтный генератор. Суть его заключалась в задании следующего числа последовательности с помощью предыдущего: 
0" alt="N, n >0" src="https://www.pvsm.ru/images/2021/12/14/nesluchainaya-sluchainost-o-roli-gpsch-v-nashei-jizni-7.svg" title="Неслучайная случайность — о роли ГПСЧ в нашей жизни - 7"/>. В данной формуле a, b, N и
являются параметрами системы. Но у этого метода есть недостатки в виде небольшого периода, равного N, и зацикливаемости последовательности.
Также хочется сказать про РСЛОС (Регистр сдвига с линейной обратной связью). Данный генератор создает следующий бит производя операции умножения и сложения по модулю два над несколькими предыдущими значениями. Данный многочлен выдает период псевдослучайной последовательности не больший, чем 
Описание РСЛОС
Рекуррентную формулу можно представить в виде:
где m - степень многолчена, а 
- коэффициенты многочлена.
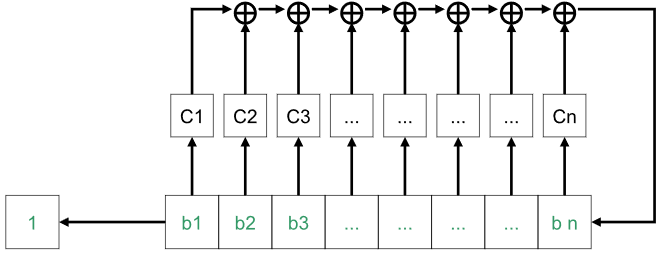
После операции суммирования, происходит сдвиг всех элементов последовательности таким образом, что полученное значение кладется в конец последовательности, а бывший первым бит подается на выход генератора.
"Вихрь Мерсенна" является одним из наиболее распространенных на данный момент ГПСЧ, а точнее его версия М199937, и реализован в стандартных библиотеках множества языков программирования. Этот алгоритм имеет большой период, равный 
и в нем тяжело выявить статистические закономерности.
Описание Вихря Мерсенна
Алгоритм генерирует двоичные слова размерностью w. Начальными значениями являются n векторов размерности w. Элемент n + p задается формулой:
где
-
p, q, r - целые константы, p - степень рекуррентности,
; -
- w-битовое двоичное число; -
- двоичное число, полученное конкатенацией чисел 
и 
где первые w-r бит взяты из первого числа, а последние r бит из второго числа; -
- матрица размером 
определенная посредством 
Далее следует процедура "закалки", которая усиливает равномерность распределения векторов большой размерности.
Подробнее можно почитать [1] стр. 55-58.
Но данный генератор не используется в криптографии, так как не удовлетворяет условиям криптостойкого ГПСЧ (КСГПСЧ):
-
КСГПСЧ должен удовлетворять "тесту на следующий бит": не должно существовать полиномиального алгоритма, который, зная первые k битов случайной последовательности, сможет предсказать k+1 бит с вероятностью, не равной ½;
-
КСГПСЧ должен оставаться надежным, даже если известна часть внутренних состояний генератора. Если в алгоритме применяется дополнительный источник энтропии, то использовать значения данного источника для взлома генератора должно быть вычислительно невозможно.
Если говорить о примерах, то такие алгоритмы как ISAAC, алгоритм Yarrow или алгоритм Blum-Blum-Shub являются криптостойкими.
О связке ГПСЧ и хорошего источника энтропии
Для генерации каких-либо непредсказуемых ключей шифрования сейчас используют КСГПСЧ и аппаратный ГИСЧ. Именно эту пару и называют современным ГСЧ.
Использование ГПСЧ в нашей жизни
Разобравшись с понятием ГПСЧ, можно рассмотреть его область применения.
В основном, генераторы случайных чисел используются различных алгоритмах шифрования. К примеру, возьмем алгоритм RSA. Для его работы необходимо получать два больших случайных простых числа: p и q. И если эти два числа будут заданы не случайно, то не исключено возникновение проблем, связанных со взломом алгоритма.
Про атаки на RSA
При нарушении случайности выбора p и q есть вероятность возникновение ситуации, в которой выясниться, что 
и 
имеют общий делитель. Таким образом можно более легким способом произвести факторизацию чисел 
и 
и, зная открытую экспоненту, взломать закрытый часть. Что в итоге приведет к компрометации двух RSA ключей.
Ещё случайные числа нашли свое место в науке при изучении различных явлений и моделей. Современная наука использует различные методы статистического анализа, в которых необходимо использование случайных чисел. В ещё большей степени ГСЧ необходимы при создании моделей реальных явлений. В случаях, когда требуется воспроизвести случайную последовательность, ГПСЧ имеет преимущество в виде начального значения, которое можно задать повторно и воспроизвести случайные числа.
В теории игр, где необходимо исследовать случайные комбинации предметов (шахматы, карты), и в теории вероятностей, которая изучает случайные величины.
Нельзя не сказать про азартные игры. ГСЧ нашли свое применение в лотереях и игровых автоматах, где необходима генерация случайных исходов. Также в компьютерных играх: раздача колоды карт, бросание костей или поведение неигровых персонажей. Везде, где можно использовать волю случая - используют машинную генерацию случайных чисел. А если знать внутреннее состояние ГПСЧ, то можно сорвать большой куш, предсказывая выходящие значения.
Заключение
Как мы видим, случайные числа прочно вошли в нашу жизнь и используются повсеместно. Но неслучайная случайность может наделать много проблем. Поэтому проверьте ваш ГПСЧ на соответствие всем стандартам вашей области прежде чем его использовать.
Список литературы
-
Слеповичев И.И. Генераторы псевдослучайных чисел
-
Википедия: ГПСЧ, ГИСЧ, ЛКГ, Вихрь Мерсенна, КСГПСЧ
-
Стандарты: NIST, ANSI, Росстандарт
Автор: Андрей Токарев
