При начальном изучении комбинационных логических схем принято использовать таблицы истинности. Это правильно, но при большом количестве входов и использовании инверторов быстро становится неудобным. Мы предлагаем альтернативный способ описания, делающий прозрачным смысл схем.
Для примера рассмотрим несколько вариантов схем:
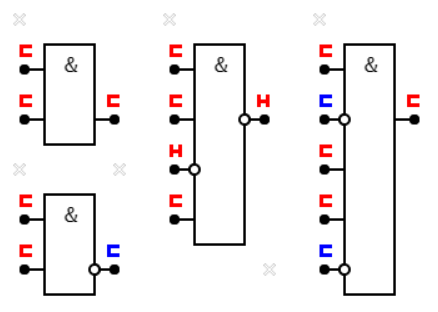
Какие различия есть между изображенными элементами? Строить для каждого таблицу истинности, скучно, поэтому сразу дадим ответ: никаких:). Все они реализуют логическое И и описываются одной строчкой (смотри ниже).
Рассмотрим реальное напряжение, которое имеется на шинах логических схем. Оно имеет
вид безобразный и ужасный:)
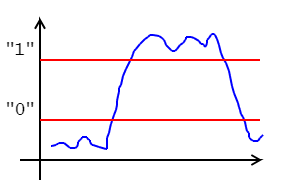
Первый уровень абстракции это когда мы отрезаем всё что ниже 0.5 вольта
и говорим что это логический 0, отрезаем всё что выше 2.5 вольта
и говорим что это логическая 1.
Он используется в большинстве учебников по цифровой технике и позволяет, в частности, строить всякого рода таблицы истинности, удобные при конструировании и оптимизации сложных логических схем.
Это удобно только при небольшом количестве входов (попробуйте начертить такую таблицу для 8-входовой схемы XOR, используемой при расчете бита четности байта, посыпьте голову пеплом и возвращайтесь к этой статье:))
Мы рассматриваем следующий уровень абстракции, а именно переходим к понятию логического сигнала.
Сигнал это не 0 и не 1, а соответствие уровня виду входа или выхода логического элемента.
Будем говорить, что на прямом входе есть сигнал, если тем логическая 1,
а на инверсном, если там логический 0 (то же и для выходов).
Наличие сигнала отмечаем на схеме буквой «с», отсутствие — буквой «н».
Логический уровень отмечаем цветом «1» — красный, «0» — синий.
Такой подход позволяет полностью отказаться от таблиц истинности.
Теперь можно вернуться к первому рисунку. На правом элементе мы видим сигналы разной полярности на всех входах и сигнал на выходе. Аналогичная маркировка имеется и на других элементах.
Переход к использованию сигналов позволяет сформулировать краткие(однострочные) их описания вне зависимости от количества входов.
Описание комбинационных схем в терминах сигналов:
на выходе инвертора (повторителя) есть сигнал, если есть сигнал на входе:
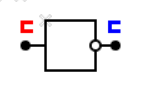
на выходе схемы «И» есть сигнал, если есть сигналы на всех входах (именно эта строчка описывает каждый элемент на первом рисунке):
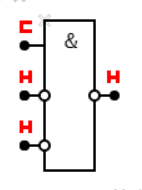
на выходе схемы «ИЛИ» есть сигнал, если есть сигнал хотя бы на одном входе:
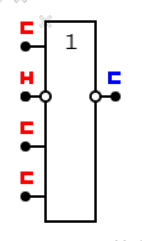
на выходе схемы «XOR» есть сигнал, если сигналы есть на нечетном числе входов:
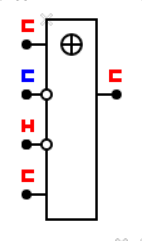
схема дешифратора (DC): сигнал появляется на выходе, номер которого задан числом на входе:
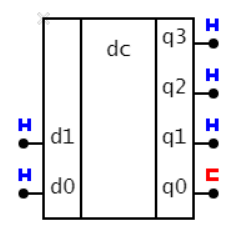
на выходах шифратора(CD) формируется номер входа, на котором есть сигнал:
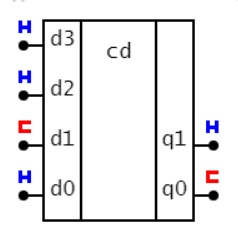
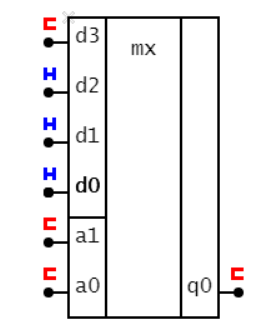
схема МХ (мультиплексор): выход повторяет вход, номер которого задан числом на адресных входах:
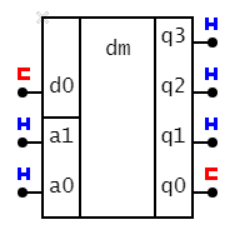
DM (демультиплексор) выход, номер которого задан числом на адресе повторяет вход:
Аналогичным образом можно описать и другие комбинационные схемы. При этом ни количество входов ни их вид (прямой, инверсный) не имеют значение. Исходя из подобного описания совершенно очевидно, в частности, доказательство теоремы де Моргана.
Человеку гораздо проще оперировать одним предложением чем объемными таблицами истинности.
Для схем с устойчивыми состояниями (триггеров, счетчиков и т. п.) набор сигналов на входах
увеличивается до 4 (добавляем фронты), сохраняя прозрачность описания, но это уже тема другого поста:)
Автор: anbglazov