Памяти моего папы, Плеханова Станислава Петровича, посвящается.
Когда необходимо синтезировать логическую схему и получить результат с минимальным числом элементов, в подавляющем числе случаев используют карты Карно. Карты Карно изучаются в высших учебных заведениях, инженерных курсах и т.д. Однако, если ваша логическая функция имеет 5-6 входов, использование карт Карно достаточно проблематично, а при большем количестве входных переменных и вовсе практически невозможно. Удивительно, но существует метод, который значительно проще и эффективней карт Карно, но о котором большинство разработчиков не знает.
Метод минимизации булевых функций, существенно более эффективный, чем другие существующие методы, основан на использовании так называемых «симметричных карт» [1,2]. Почему карты называют симметричными, будет ясно из дальнейшего рассказа. Проиллюстрирую этот метод на примере.
Пусть дана таблица истинности с пятью входными переменными, показанная на рис. 1.

Напомню, что значение "-" функции F означает «безразличное» состояние, которое говорит, что подобного набора входных переменных не возникает и значение функции может быть назначено нами произвольно нулем или единицей в процессе минимизации. Первое, что необходимо сделать, это пронумеровать входные наборы в восьмеричной системе (последний столбец на рисунке 1). После этого проводят заполнение самой симметричной карты. Симметричная карта для пяти переменных показана на рисунке 2.
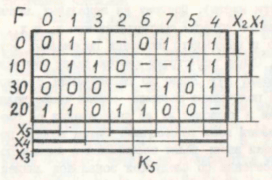
Как ее нарисовать будет показано далее, а сейчас я хочу обратить внимание на индексы столбцов, которые образуют последовательность 0, 1, 3, 2, 6, 7, 5, 4 и последовательность строк («десятков» в восьмеричной системе) — 0, 10, 30, 20.
Заполнение такой таблицы происходит значительно проще, чем карты Карно. Для этого берут восемь значений из таблицы истинности и заносят их в соответствующую строку (индексы столбцов соответстуют номеру в восьмерке входного набора). После этого приступают собственно к минимизации булевой функции. Здесь используется свойство симметрии, которое и дает название этой карте.
Минимизируем карту по единицам. Возьмем единицу в строке 0 и столбце с индексом «1». Проверяем все клетки «симметричные» данной единице. Сначала в «паре», то есть относительно вертикальной оси, проходящей между столбцами «0» и «1». Это будет клетка в строке 0 и индексом 0. Там находится значение «0», поэтому «склеивание» этих двух значений произвести нельзя. Проверяем симметрию в «четверке», то есть относительно вертикальной оси, проходящей между столбцами 1 и 3. Это клетка в строке 0 и индексом 3. Там стоит значение "-", значит, если принять его за «1», можно объединить («склеить») его с нашей единицей. Далее проверяется клетка 5 строки 0, соответствующая оси симметрии между столбцами 2 и 6 (она тоже может быть слеена с нашей единицей). Следующая симметрия в «шестнадцать» — это клетка в строке 10 и столбце 1 относительно горизонтальной оси между строками 0 и 10. И, наконец, симметрия в «тридцать два» — клетка в строке 20 и столбце 1 — с горизонтальной осью симметрии, проходящей между строками 10 и 30.
Наша задача — найти максимально возможную фигуру, склеивая нашу единичку с другими, симметричными ей. Имеется единственная такая фигура, которая покрывает клетки (строка-столбец): 0-1, 0-3, 0-7, 0-5, 10-1, 10-3, 10-7, 10-5. Чтобы получить импликанту, соответствующую этому набору, необходимо просто найти переменные, которые описывают данную группу либо в прямом либо в инверсном виде. Возьмем переменную X1 (на рисунке 2 она обозначена вертикальной прямой справа, причем строки 0 и 10 — это толстая линия, соответствующая инверсному значению, а строки 30 и 20 — тонкая линия, соответствующая прямому значению). Вся наша группа единичек попадает в строки 0 и 10, следовательно, X1 входит в нашу импликанту в инверсном виде. Переменная X2, показанная также справа, не войдет в нашу импликанту, поскольку группа попадает как в инверсное (строка 0), так и в прямое значение этой переменной (строка 10). Аналогчно, в нашу импликанту не попадут переменные X3 и X4, показанные горизонтальными линиями внизу симметричной карты, а переменная X5 войдет, поскольку вся группа единиц описывается прямым значением переменной X5. Окончательно, наша группа единиц будет представлена как (not X1)*X5.
Разобравшись с единицей в строке 0 и столбце 1, ищем оставшиеся единицы, не входящие в уже сформированные группы. Берем единицу в строке 0 и индексом 4 (последний столбец). Из нее можно получить две равновеликие группы, первая из которых содержит клетки в строках 0 и 10, индексы столбцов 5 и 4, а вторая — все клетки в последнем столбце. Группы будут соответствовать импликантам (not X1)*X3*(not X4) и X3*(not X4)*(not X5). Заметим, что если существует более одной возможности покрытия, то вариантов минимальной булевой функции также может быть более одного. Действуем так аналогично, до тех пор, пока все единицы не будут покрыты хотя-бы одной группой.
Окончательно имеем минимальную дизъюнктивно нормальную форму в виде двух вариантов:

Симметричные карты для другого количества переменных имеют аналогичный вид, который приведен на следующих рисунках.
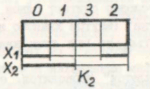


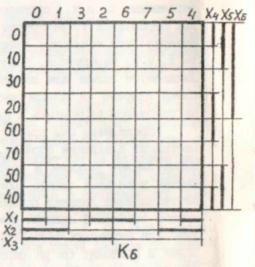
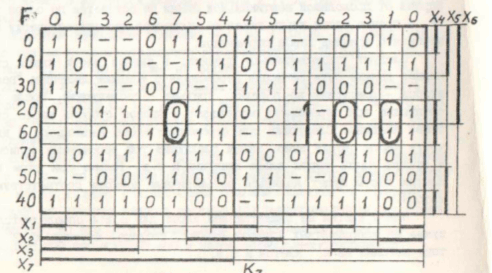
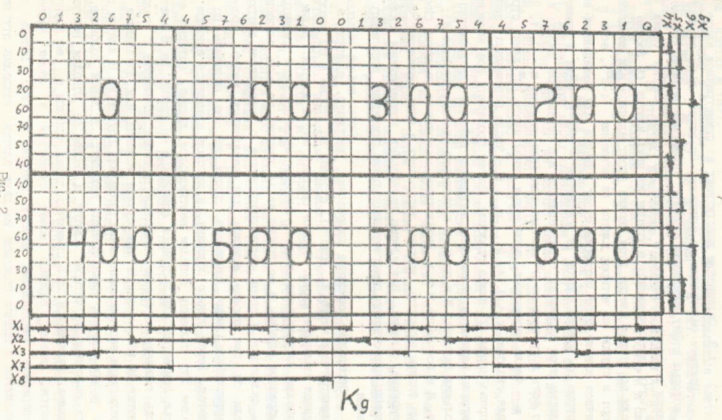
Отметим, что симметричные карты позволяют:
1. Существенно ускорить и упростить заполнение по таблице истинности.
2. В несколько раз увеличить число аргументов минимизируемой функции.
3. Существенно упростить процесс минимизации благодаря свойству симметрии.
1. Медведев С.С. Восьмеричные карты для минимизации булевых функций. Теория автоматов. Сб. статей, Институт кибернетики АН СССР, 1966, с. 45-49.
2. Плеханов С.П. Симметричные карты — мощное средство минимизации булевых функций при проектировании цифровых устройств больших размерностей. — Электронная техника, Сер. 10, Микроэлектронные устройства. — 1991. Вып. 4(88), с. 27-29.
Автор: andy_p





