[Предыдущие части анализа: первая и вторая и третья.]
Часть 1. Перистые облака
Когда действие игры происходит на открытых пространствах, одним из факторов, определяющих правдоподобность мира, является небо. Задумайтесь об этом — бОльшую часть времени небо в буквальном смысле занимает примерно 40-50% всего экрана. Небо — это намного больше, чем красивый градиент. На нём есть звёзды, солнце, луна и, наконец, облака.
Хотя современные тенденции, похоже, заключаются в объёмном рендеринге облаков при помощи raymarching-а (см. эту статью), облака в «Ведьмаке 3» полностью основаны на текстурах. Я уже рассматривал их ранее, но оказалось, что с ними всё сложнее, чем я изначально ожидал. Если вы следили за моей серией статей, то знаете, что есть разница между DLC «Кровь и вино» и остальной игрой. И, как можно догадаться, в DLC есть некоторые изменения и в работе с облаками.
В «Ведьмаке 3» есть несколько слоёв облаков. В зависимости от погоды это могут быть только перистые облака, высококучевые облака, возможно, немного облаков из семейства слоистых облаков (например, во время бури). В конце концов, облаков может не быть вовсе.
Некоторые слои отличаются с точки зрения текстур и шейдеров, используемых для их рендеринга. Очевидно, что это влияет на сложность и длину ассемблерного кода пиксельного шейдера.
Несмотря на всё это разнообразие, существуют некие общие паттерны, которые можно наблюдать при рендеринге облаков в Witcher 3. Во-первых, все они рендерятся в упреждающем проходе, и это совершенно правильный выбор. Все они используют смешивание (см. ниже). Благодаря этому гораздо проще управлять тем, как отдельный слой покрывает небо — на это влияет значение альфы из пиксельного шейдера.

Что более интересно, некоторые слои рендерятся дважды с одинаковыми параметрами.
После просмотра кода я выбрал самый короткий шейдер, чтобы (1) с наибольшей вероятностью выполнить его полный реверс-инжиниринг, (2) разобраться во всех его аспектах.
Я внимательнее присмотрелся в перистым облакам из Witcher 3: Blood and Wine.
Вот пример кадра:

До рендеринга

После первого прохода рендеринга

После второго прохода рендеринга
В этом конкретном кадре перистые облака — это первый слой при рендеринге. Как вы видите, он рендерится дважды, что повышает его яркость.
Геометрический и вершинный шейдер
Перед пиксельным шейдером вкратце расскажем об использованном геометрическом и вершинном шейдере. Меш для отображения облаков немного похож на обычный купол неба:

Все вершины находятся в интервале [0-1], поэтому чтобы центрировать меш на точке (0,0,0), перед преобразованием в worldViewProj используются масштабирование и отклонение (нам уже знаком этот паттерн из предыдущих частей серии). В случае облаков меш сильно растягивается вдоль плоскости XY (ось Z направлена вверх), чтобы закрыть больше пространства, чем пирамида видимости. Результат получается таким:
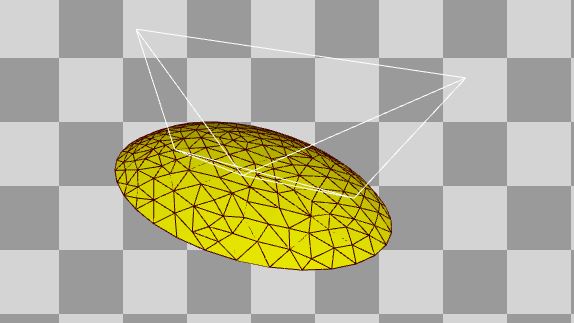
Кроме этого, меш имеет векторы нормалей и касательных. Также вершинный шейдер векторным произведением вычисляет вектор бикасательной — все три выводятся в нормализованном виде. Ещё присутствует повершинное вычисление тумана (его цвет и яркость).
Пиксельный шейдер
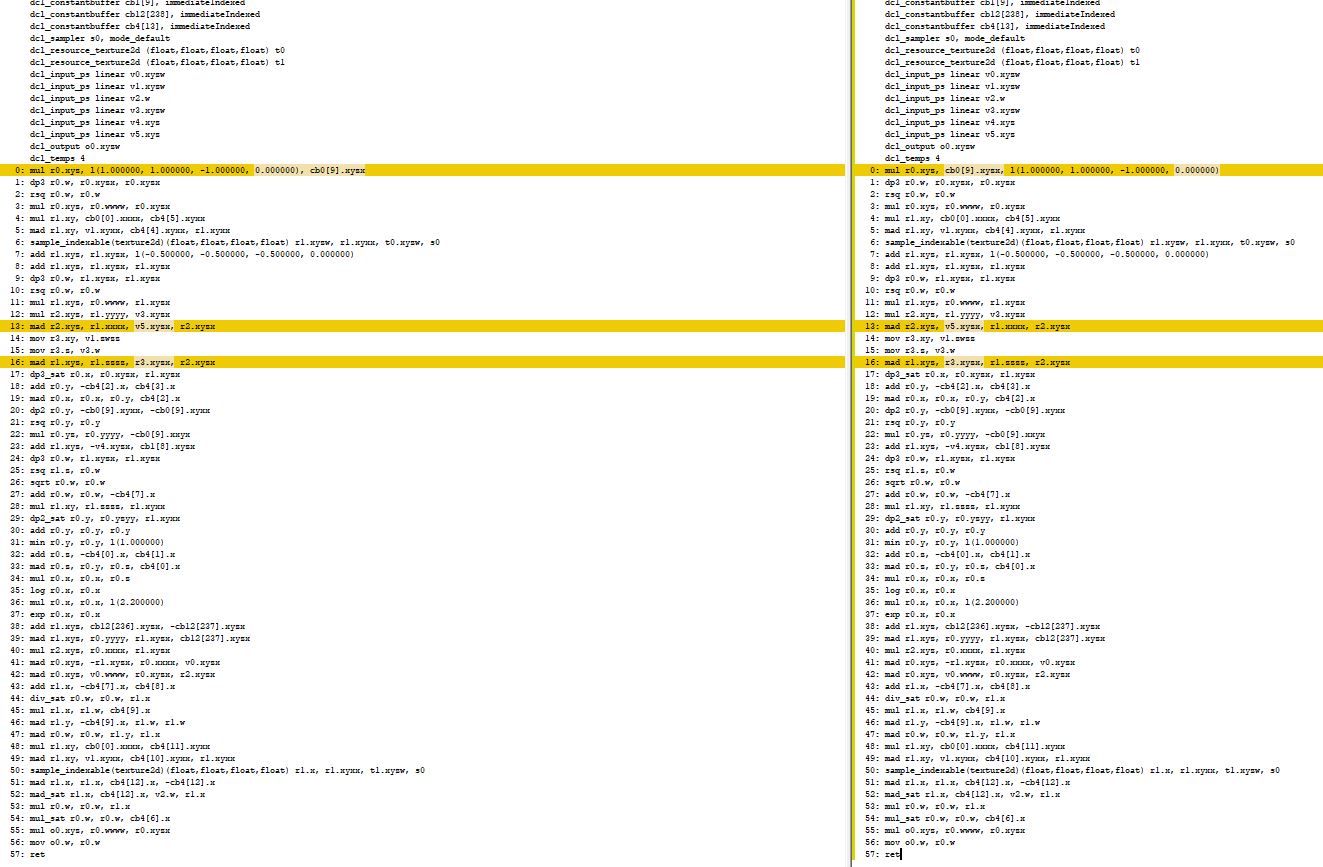
Ассемблерный код пиксельного шейдера выглядит так:
ps_5_0
dcl_globalFlags refactoringAllowed
dcl_constantbuffer cb0[10], immediateIndexed
dcl_constantbuffer cb1[9], immediateIndexed
dcl_constantbuffer cb12[238], immediateIndexed
dcl_constantbuffer cb4[13], immediateIndexed
dcl_sampler s0, mode_default
dcl_resource_texture2d (float,float,float,float) t0
dcl_resource_texture2d (float,float,float,float) t1
dcl_input_ps linear v0.xyzw
dcl_input_ps linear v1.xyzw
dcl_input_ps linear v2.w
dcl_input_ps linear v3.xyzw
dcl_input_ps linear v4.xyz
dcl_input_ps linear v5.xyz
dcl_output o0.xyzw
dcl_temps 4
0: mul r0.xyz, cb0[9].xyzx, l(1.000000, 1.000000, -1.000000, 0.000000)
1: dp3 r0.w, r0.xyzx, r0.xyzx
2: rsq r0.w, r0.w
3: mul r0.xyz, r0.wwww, r0.xyzx
4: mul r1.xy, cb0[0].xxxx, cb4[5].xyxx
5: mad r1.xy, v1.xyxx, cb4[4].xyxx, r1.xyxx
6: sample_indexable(texture2d)(float,float,float,float) r1.xyzw, r1.xyxx, t0.xyzw, s0
7: add r1.xyz, r1.xyzx, l(-0.500000, -0.500000, -0.500000, 0.000000)
8: add r1.xyz, r1.xyzx, r1.xyzx
9: dp3 r0.w, r1.xyzx, r1.xyzx
10: rsq r0.w, r0.w
11: mul r1.xyz, r0.wwww, r1.xyzx
12: mul r2.xyz, r1.yyyy, v3.xyzx
13: mad r2.xyz, v5.xyzx, r1.xxxx, r2.xyzx
14: mov r3.xy, v1.zwzz
15: mov r3.z, v3.w
16: mad r1.xyz, r3.xyzx, r1.zzzz, r2.xyzx
17: dp3_sat r0.x, r0.xyzx, r1.xyzx
18: add r0.y, -cb4[2].x, cb4[3].x
19: mad r0.x, r0.x, r0.y, cb4[2].x
20: dp2 r0.y, -cb0[9].xyxx, -cb0[9].xyxx
21: rsq r0.y, r0.y
22: mul r0.yz, r0.yyyy, -cb0[9].xxyx
23: add r1.xyz, -v4.xyzx, cb1[8].xyzx
24: dp3 r0.w, r1.xyzx, r1.xyzx
25: rsq r1.z, r0.w
26: sqrt r0.w, r0.w
27: add r0.w, r0.w, -cb4[7].x
28: mul r1.xy, r1.zzzz, r1.xyxx
29: dp2_sat r0.y, r0.yzyy, r1.xyxx
30: add r0.y, r0.y, r0.y
31: min r0.y, r0.y, l(1.000000)
32: add r0.z, -cb4[0].x, cb4[1].x
33: mad r0.z, r0.y, r0.z, cb4[0].x
34: mul r0.x, r0.x, r0.z
35: log r0.x, r0.x
36: mul r0.x, r0.x, l(2.200000)
37: exp r0.x, r0.x
38: add r1.xyz, cb12[236].xyzx, -cb12[237].xyzx
39: mad r1.xyz, r0.yyyy, r1.xyzx, cb12[237].xyzx
40: mul r2.xyz, r0.xxxx, r1.xyzx
41: mad r0.xyz, -r1.xyzx, r0.xxxx, v0.xyzx
42: mad r0.xyz, v0.wwww, r0.xyzx, r2.xyzx
43: add r1.x, -cb4[7].x, cb4[8].x
44: div_sat r0.w, r0.w, r1.x
45: mul r1.x, r1.w, cb4[9].x
46: mad r1.y, -cb4[9].x, r1.w, r1.w
47: mad r0.w, r0.w, r1.y, r1.x
48: mul r1.xy, cb0[0].xxxx, cb4[11].xyxx
49: mad r1.xy, v1.xyxx, cb4[10].xyxx, r1.xyxx
50: sample_indexable(texture2d)(float,float,float,float) r1.x, r1.xyxx, t1.xyzw, s0
51: mad r1.x, r1.x, cb4[12].x, -cb4[12].x
52: mad_sat r1.x, cb4[12].x, v2.w, r1.x
53: mul r0.w, r0.w, r1.x
54: mul_sat r0.w, r0.w, cb4[6].x
55: mul o0.xyz, r0.wwww, r0.xyzx
56: mov o0.w, r0.w
57: ret На вход подаются две бесшовные текстуры. Одна из них содержит карту нормалей (каналы xyz) и форму облака (канал a). Вторая — это шум для искажения формы.

Карта нормалей, собственность CD Projekt Red
Форма облака, собственность CD Projekt Red

Текстура шума, собственность CD Projekt Red
Основной буфер констант с параметрами облаков — это cb4. Для данного кадра он имеет следующие значения:
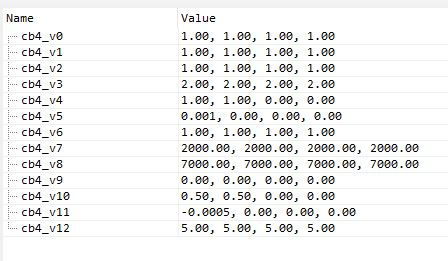
Кроме этого, используются другие значения из других cbuffer-ов. Не волнуйтесь, их мы тоже рассмотрим.
Инвертированное по оси Z направление солнечного света
Первое, что происходит в шейдере — вычисление нормализованного направления солнечного света, инвертированного по оси Z:
0: mul r0.xyz, cb0[9].xyzx, l(1.000000, 1.000000, -1.000000, 0.000000)
1: dp3 r0.w, r0.xyzx, r0.xyzx
2: rsq r0.w, r0.w
3: mul r0.xyz, r0.wwww, r0.xyzx
float3 invertedSunlightDir = normalize(lightDir * float3(1, 1, -1) );Как говорилось ранее, ось Z направлена вверх, а cb0[9] — это направление солнечного света. Этот вектор направлен на Солнце — это важно! Вы можете убедиться в этом, написав простой вычислительный шейдер, выполняющий простое NdotL, и вставив его в проход отложенного затенения.
Сэмплирование текстуры облаков
Следующий шаг — это вычисление texcoords для сэмплирования текстуры облаков, распаковка вектора нормали и его нормализация.
4: mul r1.xy, cb0[0].xxxx, cb4[5].xyxx
5: mad r1.xy, v1.xyxx, cb4[4].xyxx, r1.xyxx
6: sample_indexable(texture2d)(float,float,float,float) r1.xyzw, r1.xyxx, t0.xyzw, s0
7: add r1.xyz, r1.xyzx, l(-0.500000, -0.500000, -0.500000, 0.000000)
8: add r1.xyz, r1.xyzx, r1.xyzx
9: dp3 r0.w, r1.xyzx, r1.xyzx
10: rsq r0.w, r0.w
// Calc sampling coords
float2 cloudTextureUV = Texcoords * textureScale + elapsedTime * speedFactors;
// Sample texture and get data from it
float4 cloudTextureValue = texture0.Sample( sampler0, cloudTextureUV ).rgba;
float3 normalMap = cloudTextureValue.xyz;
float cloudShape = cloudTextureValue.a;
// Unpack normal and normalize it
float3 unpackedNormal = (normalMap - 0.5) * 2.0;
unpackedNormal = normalize(unpackedNormal);Давайте постепенно с этим разбираться.
Чтобы получить движение облаков, нам необходимо прошедшее время в секундах (cb[0].x) умноженное на коэффициент скорости, влияющий на то, как быстро облака движутся по небу (cb4[5].xy).
Как я говорил ранее, UV растянуты по геометрии купола неба, и нам также нужны коэффициенты масштабирования текстур, влияющие на размер облаков (cb4[4].xy).
Окончательная формула имеет вид:
samplingUV = Input.TextureUV * textureScale + time * speedMultiplier;После сэмплирования всех 4 каналов у нас есть карта нормалей (каналы rgb) и форма облака (канал a).
Для распаковки карты нормалей из интервала [0; 1] в интервал [-1; 1] мы используем следующую формулу:
unpackedNormal = (packedNormal - 0.5) * 2.0;Также можно использовать такую:
unpackedNormal = packedNormal * 2.0 - 1.0;И наконец мы нормализуем распакованный вектор нормали.
Наложение нормалей
Имея векторы нормали, касательной и бикасательной из вершинного шейдера и вектор нормали из карты нормалей, мы обычным способом выполняем наложение нормалей.
11: mul r1.xyz, r0.wwww, r1.xyzx
12: mul r2.xyz, r1.yyyy, v3.xyzx
13: mad r2.xyz, v5.xyzx, r1.xxxx, r2.xyzx
14: mov r3.xy, v1.zwzz
15: mov r3.z, v3.w
16: mad r1.xyz, r3.xyzx, r1.zzzz, r2.xyzx
// Perform bump mapping
float3 SkyTangent = Input.Tangent;
float3 SkyNormal = (float3( Input.Texcoords.zw, Input.param3.w ));
float3 SkyBitangent = Input.param3.xyz;
float3x3 TBN = float3x3(SkyTangent, SkyBitangent, SkyNormal);
float3 finalNormal = (float3)mul( unpackedNormal, (TBN) );Яркость засветов (1)
В следующем шаге применяется вычисление NdotL и это влияет на величину засветки определённого пикселя.
Рассмотрим следующий ассемблерный код:
17: dp3_sat r0.x, r0.xyzx, r1.xyzx
18: add r0.y, -cb4[2].x, cb4[3].x
19: mad r0.x, r0.x, r0.y, cb4[2].x Вот визуализация NdotL на рассматриваемом кадре:

Это скалярное произведение (с насыщенностью) используется для выполнения интерполяции между minIntensity и maxIntensity. Благодаря этому части облаков, освещённые солнечным светом, будут более яркими.
// Calculate cosine between normal and up-inv lightdir
float NdotL = saturate( dot(invertedSunlightDir, finalNormal) );
// Param 1, line 19, r0.x
float intensity1 = lerp( param1Min, param1Max, NdotL );Яркость засветов (2)
Есть ещё один фактор, влияющий на яркость облаков.
Облака, находящиеся в той части неба, где есть солнце, должны быть более подсвеченными. Для этого мы вычисляем градиент на основании плоскости XY.
Этот градиент используется для вычисления линейной интерполяции между значениями min/max, аналогично тому, что происходит в части (1).
То есть теоретически мы можем попросить затемнить облака, находящиеся на противоположной от солнца стороне, но в данном конкретном кадре этого не происходит, потому что param2Min и param2Max (cb4[0].x и cb4[1].x) присвоено значение 1.0f.
20: dp2 r0.y, -cb0[9].xyxx, -cb0[9].xyxx
21: rsq r0.y, r0.y
22: mul r0.yz, r0.yyyy, -cb0[9].xxyx
23: add r1.xyz, -v4.xyzx, cb1[8].xyzx
24: dp3 r0.w, r1.xyzx, r1.xyzx
25: rsq r1.z, r0.w
26: sqrt r0.w, r0.w
27: add r0.w, r0.w, -cb4[7].x
28: mul r1.xy, r1.zzzz, r1.xyxx
29: dp2_sat r0.y, r0.yzyy, r1.xyxx
30: add r0.y, r0.y, r0.y
31: min r0.y, r0.y, l(1.000000)
32: add r0.z, -cb4[0].x, cb4[1].x
33: mad r0.z, r0.y, r0.z, cb4[0].x
34: mul r0.x, r0.x, r0.z
35: log r0.x, r0.x
36: mul r0.x, r0.x, l(2.200000)
37: exp r0.x, r0.x
// Calculate normalized -lightDir.xy (20-22)
float2 lightDirXY = normalize( -lightDir.xy );
// Calculate world to camera
float3 vWorldToCamera = ( CameraPos - WorldPos );
float worldToCamera_distance = length(vWorldToCamera);
// normalize vector
vWorldToCamera = normalize( vWorldToCamera );
float LdotV = saturate( dot(lightDirXY, vWorldToCamera.xy) );
float highlightedSkySection = saturate( 2*LdotV );
float intensity2 = lerp( param2Min, param2Max, highlightedSkySection );
float finalIntensity = pow( intensity2 *intensity1, 2.2);В самом конце мы перемножаем обе яркости и возводим результат в степень 2.2.
Цвет облаков
Вычисление цвета облаков начинается с получения из буфера констант двух значений, обозначающих цвет облаков рядом с солнцем и облаков на противоположной части неба. Между ними выполняется линейная интерполяция на основании highlightedSkySection.
Затем результат умножается на finalIntensity.
А в конце результат смешивается с туманом (из соображений производительности он был вычислен вершинным шейдером).
38: add r1.xyz, cb12[236].xyzx, -cb12[237].xyzx
39: mad r1.xyz, r0.yyyy, r1.xyzx, cb12[237].xyzx
40: mul r2.xyz, r0.xxxx, r1.xyzx
41: mad r0.xyz, -r1.xyzx, r0.xxxx, v0.xyzx
42: mad r0.xyz, v0.wwww, r0.xyzx, r2.xyzx
float3 cloudsColor = lerp( cloudsColorBack, cloudsColorFront, highlightedSunSection );
cloudsColor *= finalIntensity;
cloudsColor = lerp( cloudsColor, FogColor, FogAmount );Делаем так, чтобы перистые облака были сильнее заметны на горизонте
На кадре этого не очень заметно, но на самом деле этот слой более видим рядом с горизонтом, чем над головой Геральта. Вот как это делается.
Можно было заметить, что при вычислении второй яркости мы вычислили длину вектора worldToCamera:
23: add r1.xyz, -v4.xyzx, cb1[8].xyzx
24: dp3 r0.w, r1.xyzx, r1.xyzx
25: rsq r1.z, r0.w
26: sqrt r0.w, r0.wДавайте найдём следующие вхождения этой длины в коде:
26: sqrt r0.w, r0.w
27: add r0.w, r0.w, -cb4[7].x
...
43: add r1.x, -cb4[7].x, cb4[8].x
44: div_sat r0.w, r0.w, r1.xОго, что это тут у нас?
cb[7].x и cb[8].x имеют значения 2000.0 и 7000.0.
Оказывается, что это результат применения функции linstep.
Она получает три параметра: min/max — интервал и v — значение.
Это работает следующим образом: если v находится в интервале [min-max], то функция возвращает линейную интерполяцию в интервале [0.0 — 1.0]. С другой стороны, если v находится вне интервала, то linstep возвращает 0.0 или 1.0.
Простой пример:
linstep( 1000.0, 2000.0, 999.0) = 0.0
linstep( 1000.0, 2000.0, 1500.0) = 0.5
linstep( 1000.0, 2000.0, 2000.0) = 1.0То есть она довольно похожа на smoothstep из HLSL, за исключением того, что в этом случае вместо эрмитовой интерполяции выполняется линейная.
Функции Linstep нет в HLSL, но она очень полезна. Стоит иметь её в своём инструментарии.
// linstep:
//
// Returns a linear interpolation between 0 and 1 if t is in the range [min, max]
// if "v" is <= min, the output is 0
// if "v" i >= max, the output is 1
float linstep( float min, float max, float v )
{
return saturate( (v - min) / (max - min) );
} Вернёмся к Witcher 3: после вычисления этого показателя, сообщающего, насколько далеко конкретная часть неба находится от Геральта, мы используем его для ослабления яркости облаков:
45: mul r1.x, r1.w, cb4[9].x
46: mad r1.y, -cb4[9].x, r1.w, r1.w
47: mad r0.w, r0.w, r1.y, r1.x
float distanceAttenuation = linstep( fadeDistanceStart, fadeDistanceEnd, worldToCamera_distance );
float fadedCloudShape = closeCloudsHidingFactor * cloudShape;
cloudShape = lerp( fadedCloudShape, cloudShape, distanceAttenuation );cloudShape — это канал .a из первой текстуры, а closeCloudsHidingFactor — значение из буфера констант, управляющее уровнем видимости облаков над головой Геральта. Во всех протестированных мной кадрах оно было равно 0.0, что равносильно отсутствию облаков. Когда distanceAttenuation приближается к 1.0 (расстояние от камеры до купола неба увеличивается), облака становятся всё более видимыми.
Сэмплирование текстуры шума
Вычисление координат сэмплирования текстуры шума аналогично вычислениям для текстуры облаков, за исключением того, что используется другой набор textureScale и speedMultiplier.
Разумеется, для сэмплирования всех этих текстур используется сэмплер со включенным режимом адресации wrap.
48: mul r1.xy, cb0[0].xxxx, cb4[11].xyxx
49: mad r1.xy, v1.xyxx, cb4[10].xyxx, r1.xyxx
50: sample_indexable(texture2d)(float,float,float,float) r1.x, r1.xyxx, t1.xyzw, s0
// Calc sampling coords for noise
float2 noiseTextureUV = Texcoords * textureScaleNoise + elapsedTime * speedFactorsNoise;
// Sample texture and get data from it
float noiseTextureValue = texture1.Sample( sampler0, noiseTextureUV ).x;Соединяем всё это вместе
Получив значение шума, мы должны скомбинировать его с cloudShape.
У меня возникли некоторые проблемы с пониманием этих строк, где есть param2.w (который всегда равен 1.0) и noiseMult (имеет значение 5.0, взятое из буфера констант).
Как бы то ни было, самое важное здесь — это окончательное значение generalCloudsVisibility, влияющее на степень видимости облаков.
Взгляните также на окончательное значение шума. Выходной цвет cloudsColor умножается на окончательный шум, который тоже выводится в альфа-канал.
51: mad r1.x, r1.x, cb4[12].x, -cb4[12].x
52: mad_sat r1.x, cb4[12].x, v2.w, r1.x
53: mul r0.w, r0.w, r1.x
54: mul_sat r0.w, r0.w, cb4[6].x
55: mul o0.xyz, r0.wwww, r0.xyzx
56: mov o0.w, r0.w
57: ret
// Sample noise texture and get data from it
float noiseTextureValue = texture1.Sample( sampler0, noiseTextureUV ).x;
noiseTextureValue = noiseTextureValue * noiseMult - noiseMult;
float noiseValue = saturate( noiseMult * Input.param2.w + noiseTextureValue);
noiseValue *= cloudShape;
float finalNoise = saturate( noiseValue * generalCloudsVisibility);
return float4( cloudsColor*finalNoise, finalNoise ); Итог
Готовый результат выглядит очень правдоподобным.
Можете сравнить. Первая картинка — мой шейдер, вторая — шейдер игры:
Если вам любопытно, то шейдер выложен здесь.
Часть 2. Туман
Туман можно реализовать различными способами. Однако времена, когда мы могли наложить простой зависящий от расстояния туман и покончить с этим, остались навсегда в прошлом (скорее всего). Жизнь в мире программируемых шейдеров открыла нам двери к новым безумным, но, что более важно, — физически точным и визуально реалистичным решениям.
Современные тенденции в рендеринге тумана основаны на вычислительных шейдерах (подробности см. в этой презентации Барта Вронски ).
Несмотря на то, что эта презентация появилась в 2014 году, а «Ведьмак 3» был выпущен в 2015/2016 годах, туман в последней части приключений Геральта полностью зависит от экрана и реализован как типичная постобработка.
Прежде чем мы начнём очередную сессию реверс-инжиниринга, должен сказать, что за прошлый год я пытался разобраться в тумане Witcher 3 по крайней мере пять раз, и каждый раз терпел неудачу. Ассемблерный код, как вы скоро увидите, довольно сложен, и это делает процесс создания удобочитаемого шейдера тумана на HLSL почти невозможным.
Однако мне удалось найти в Интернете шейдер тумана, который сразу же привлёк моё внимание благодаря своей схожести с туманом «Ведьмака 3» с точки зрения имён переменных и общего порядка инструкций. Этот шейдер не был точно таким же, как в игре, поэтому мне пришлось его немного переработать. Я хочу этим сказать, что основная часть кода на HLSL, который вы здесь увидите, была, за двумя исключениями, создана/проанализирована не мной. Помните об этом.
Вот ассемблерный код пиксельного шейдера тумана — стоит заметить, что он одинаков для всей игры (основной части 2015 года и обеих DLC):
ps_5_0
dcl_globalFlags refactoringAllowed
dcl_constantbuffer cb3[2], immediateIndexed
dcl_constantbuffer cb12[214], immediateIndexed
dcl_resource_texture2d (float,float,float,float) t0
dcl_resource_texture2d (float,float,float,float) t1
dcl_resource_texture2d (float,float,float,float) t2
dcl_input_ps_siv v0.xy, position
dcl_output o0.xyzw
dcl_temps 7
0: ftou r0.xy, v0.xyxx
1: mov r0.zw, l(0, 0, 0, 0)
2: ld_indexable(texture2d)(float,float,float,float) r1.x, r0.xyww, t0.xyzw
3: mad r1.y, r1.x, cb12[22].x, cb12[22].y
4: lt r1.y, r1.y, l(1.000000)
5: if_nz r1.y
6: utof r1.yz, r0.xxyx
7: mul r2.xyzw, r1.zzzz, cb12[211].xyzw
8: mad r2.xyzw, cb12[210].xyzw, r1.yyyy, r2.xyzw
9: mad r1.xyzw, cb12[212].xyzw, r1.xxxx, r2.xyzw
10: add r1.xyzw, r1.xyzw, cb12[213].xyzw
11: div r1.xyz, r1.xyzx, r1.wwww
12: ld_indexable(texture2d)(float,float,float,float) r2.xyz, r0.xyww, t1.xyzw
13: ld_indexable(texture2d)(float,float,float,float) r0.x, r0.xyzw, t2.xyzw
14: max r0.x, r0.x, cb3[1].x
15: add r0.yzw, r1.xxyz, -cb12[0].xxyz
16: dp3 r1.x, r0.yzwy, r0.yzwy
17: sqrt r1.x, r1.x
18: add r1.y, r1.x, -cb3[0].x
19: add r1.zw, -cb3[0].xxxz, cb3[0].yyyw
20: div_sat r1.y, r1.y, r1.z
21: mad r1.y, r1.y, r1.w, cb3[0].z
22: add r0.x, r0.x, l(-1.000000)
23: mad r0.x, r1.y, r0.x, l(1.000000)
24: div r0.yzw, r0.yyzw, r1.xxxx
25: mad r1.y, r0.w, cb12[22].z, cb12[0].z
26: add r1.x, r1.x, -cb12[22].z
27: max r1.x, r1.x, l(0)
28: min r1.x, r1.x, cb12[42].z
29: mul r1.z, r0.w, r1.x
30: mul r1.w, r1.x, cb12[43].x
31: mul r1.zw, r1.zzzw, l(0.000000, 0.000000, 0.062500, 0.062500)
32: dp3 r0.y, cb12[38].xyzx, r0.yzwy
33: add r0.z, r0.y, cb12[42].x
34: add r0.w, cb12[42].x, l(1.000000)
35: div_sat r0.z, r0.z, r0.w
36: add r0.w, -cb12[43].z, cb12[43].y
37: mad r0.z, r0.z, r0.w, cb12[43].z
38: mul r0.w, abs(r0.y), abs(r0.y)
39: mad_sat r2.w, r1.x, l(0.002000), l(-0.300000)
40: mul r0.w, r0.w, r2.w
41: lt r0.y, l(0), r0.y
42: movc r3.xyz, r0.yyyy, cb12[39].xyzx, cb12[41].xyzx
43: add r3.xyz, r3.xyzx, -cb12[40].xyzx
44: mad r3.xyz, r0.wwww, r3.xyzx, cb12[40].xyzx
45: movc r4.xyz, r0.yyyy, cb12[45].xyzx, cb12[47].xyzx
46: add r4.xyz, r4.xyzx, -cb12[46].xyzx
47: mad r4.xyz, r0.wwww, r4.xyzx, cb12[46].xyzx
48: ge r0.y, r1.x, cb12[48].y
49: if_nz r0.y
50: add r0.y, r1.y, cb12[42].y
51: mul r0.w, r0.z, r0.y
52: mul r1.y, r0.z, r1.z
53: mad r5.xyzw, r1.yyyy, l(16.000000, 15.000000, 14.000000, 13.000000), r0.wwww
54: max r5.xyzw, r5.xyzw, l(0, 0, 0, 0)
55: add r5.xyzw, r5.xyzw, l(1.000000, 1.000000, 1.000000, 1.000000)
56: div_sat r5.xyzw, r1.wwww, r5.xyzw
57: add r5.xyzw, -r5.xyzw, l(1.000000, 1.000000, 1.000000, 1.000000)
58: mul r1.z, r5.y, r5.x
59: mul r1.z, r5.z, r1.z
60: mul r1.z, r5.w, r1.z
61: mad r5.xyzw, r1.yyyy, l(12.000000, 11.000000, 10.000000, 9.000000), r0.wwww
62: max r5.xyzw, r5.xyzw, l(0, 0, 0, 0)
63: add r5.xyzw, r5.xyzw, l(1.000000, 1.000000, 1.000000, 1.000000)
64: div_sat r5.xyzw, r1.wwww, r5.xyzw
65: add r5.xyzw, -r5.xyzw, l(1.000000, 1.000000, 1.000000, 1.000000)
66: mul r1.z, r1.z, r5.x
67: mul r1.z, r5.y, r1.z
68: mul r1.z, r5.z, r1.z
69: mul r1.z, r5.w, r1.z
70: mad r5.xyzw, r1.yyyy, l(8.000000, 7.000000, 6.000000, 5.000000), r0.wwww
71: max r5.xyzw, r5.xyzw, l(0, 0, 0, 0)
72: add r5.xyzw, r5.xyzw, l(1.000000, 1.000000, 1.000000, 1.000000)
73: div_sat r5.xyzw, r1.wwww, r5.xyzw
74: add r5.xyzw, -r5.xyzw, l(1.000000, 1.000000, 1.000000, 1.000000)
75: mul r1.z, r1.z, r5.x
76: mul r1.z, r5.y, r1.z
77: mul r1.z, r5.z, r1.z
78: mul r1.z, r5.w, r1.z
79: mad r5.xy, r1.yyyy, l(4.000000, 3.000000, 0.000000, 0.000000), r0.wwww
80: max r5.xy, r5.xyxx, l(0, 0, 0, 0)
81: add r5.xy, r5.xyxx, l(1.000000, 1.000000, 0.000000, 0.000000)
82: div_sat r5.xy, r1.wwww, r5.xyxx
83: add r5.xy, -r5.xyxx, l(1.000000, 1.000000, 0.000000, 0.000000)
84: mul r1.z, r1.z, r5.x
85: mul r1.z, r5.y, r1.z
86: mad r0.w, r1.y, l(2.000000), r0.w
87: max r0.w, r0.w, l(0)
88: add r0.w, r0.w, l(1.000000)
89: div_sat r0.w, r1.w, r0.w
90: add r0.w, -r0.w, l(1.000000)
91: mul r0.w, r0.w, r1.z
92: mad r0.y, r0.y, r0.z, r1.y
93: max r0.y, r0.y, l(0)
94: add r0.y, r0.y, l(1.000000)
95: div_sat r0.y, r1.w, r0.y
96: add r0.y, -r0.y, l(1.000000)
97: mad r0.y, -r0.w, r0.y, l(1.000000)
98: add r0.z, r1.x, -cb12[48].y
99: mul_sat r0.z, r0.z, cb12[48].z
100: else
101: mov r0.yz, l(0.000000, 1.000000, 0.000000, 0.000000)
102: endif
103: log r0.y, r0.y
104: mul r0.w, r0.y, cb12[42].w
105: exp r0.w, r0.w
106: mul r0.y, r0.y, cb12[48].x
107: exp r0.y, r0.y
108: mul r0.yw, r0.yyyw, r0.zzzz
109: mad_sat r1.xy, r0.wwww, cb12[189].xzxx, cb12[189].ywyy
110: add r5.xyz, -r3.xyzx, cb12[188].xyzx
111: mad r5.xyz, r1.xxxx, r5.xyzx, r3.xyzx
112: add r0.z, cb12[188].w, l(-1.000000)
113: mad r0.z, r1.y, r0.z, l(1.000000)
114: mul_sat r5.w, r0.z, r0.w
115: lt r0.z, l(0), cb12[192].x
116: if_nz r0.z
117: mad_sat r1.xy, r0.wwww, cb12[191].xzxx, cb12[191].ywyy
118: add r6.xyz, -r3.xyzx, cb12[190].xyzx
119: mad r3.xyz, r1.xxxx, r6.xyzx, r3.xyzx
120: add r0.z, cb12[190].w, l(-1.000000)
121: mad r0.z, r1.y, r0.z, l(1.000000)
122: mul_sat r3.w, r0.z, r0.w
123: add r1.xyzw, -r5.xyzw, r3.xyzw
124: mad r5.xyzw, cb12[192].xxxx, r1.xyzw, r5.xyzw
125: endif
126: mul r0.z, r0.x, r5.w
127: mul r0.x, r0.x, r0.y
128: dp3 r0.y, l(0.333000, 0.555000, 0.222000, 0.000000), r2.xyzx
129: mad r1.xyz, r0.yyyy, r4.xyzx, -r2.xyzx
130: mad r0.xyw, r0.xxxx, r1.xyxz, r2.xyxz
131: add r1.xyz, -r0.xywx, r5.xyzx
132: mad r0.xyz, r0.zzzz, r1.xyzx, r0.xywx
133: else
134: mov r0.xyz, l(0, 0, 0, 0)
135: endif
136: mov o0.xyz, r0.xyzx
137: mov o0.w, l(1.000000)
138: ret Честно говоря, шейдер довольно длинный. Вероятно, слишком длинный для эффективного процесса обратной разработки.
Вот пример закатной сцены с туманом:

Давайте взглянем на входящие данные:
Что касается текстур, то у нас есть буфер глубин, Ambient Occlusion и буфер HDR-цветов.

Входящий буфер глубин

Входящее ambient occlusion

Входящий буфер HDR-цвета
… а результат применения шейдера тумана в этой сцене выглядит так:

HDR-текстура после применения тумана
Буфер глубин используется для воссоздания позиции в мире. Это стандартный паттерн для шейдеров Witcher 3.
Наличие данных ambient occlusion (если они включены) позволяет нам затемнить туман. Очень умная идея, возможно, очевидная, но я никогда не думал об этом таким образом. Позже я вернусь к этому аспекту.
Шейдер начинается с определения того, находится ли пиксель на небе. В случае, если пиксель лежит на небе (depth == 1.0), шейдер возвращает чёрный цвет. Если пиксель находится в сцене (depth < 1.0), то мы воссоздаём позицию в мире при помощи буфера глубин (строки 7-11) и продолжаем вычисление тумана.
Проход тумана происходит вскоре после процесса отложенного затенения. Вы можете заметить, что некоторые относящиеся к упреждающему проходу элементы пока отсутствуют. В этой конкретной сцене были применены отложенные объёмы освещения, а после этого мы отрендерили волосы/лицо/глаза Геральта.
Первое, что нужно знать о тумане в «Ведьмаке 3»: он состоит из двух частей — «цвета тумана» и «цвета атмосферы».
struct FogResult
{
float4 paramsFog; // RGB: color, A: influence
float4 paramsAerial; // RGB: color, A: influence
};Для каждой части есть три цвета: передний, средний и задний. То есть в буфере констант есть такие данные, как «FogColorFront», «FogColorMiddle», «AerialColorBack» и т.п… Посмотрим на входящие данные:
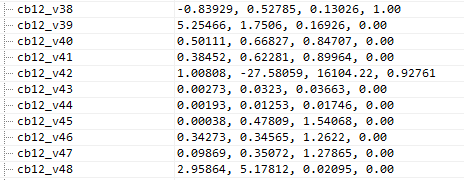
// *** Inputs *** //
float3 FogSunDir = cb12_v38.xyz;
float3 FogColorFront = cb12_v39.xyz;
float3 FogColorMiddle = cb12_v40.xyz;
float3 FogColorBack = cb12_v41.xyz;
float4 FogBaseParams = cb12_v42;
float4 FogDensityParamsScene = cb12_v43;
float4 FogDensityParamsSky = cb12_v44;
float3 AerialColorFront = cb12_v45.xyz;
float3 AerialColorMiddle = cb12_v46.xyz;
float3 AerialColorBack = cb12_v47.xyz;
float4 AerialParams = cb12_v48;Перед вычислением окончательных цветов нам нужно вычислить векторы и скалярные произведения. Шейдер имеет доступ к позиции пикселя в мире, позиции камеры (cb12[0].xyz) и направлению тумана/освещения (cb12[38].xyz). Это позволяет нам вычислить скалярное произведение вектора вида и направления тумана.
float3 frag_vec = fragPosWorldSpace.xyz - customCameraPos.xyz;
float frag_dist = length(frag_vec);
float3 frag_dir = frag_vec / frag_dist;
float dot_fragDirSunDir = dot(GlobalLightDirection.xyz, frag_dir);Для вычисления смешивающегося градиента нужно использовать квадрат абсолютного скалярного произведения, а затем снова умножить результат на какой-то параметр, зависящий от расстояния:
float3 curr_col_fog;
float3 curr_col_aerial;
{
float _dot = dot_fragDirSunDir;
float _dd = _dot;
{
const float _distOffset = -150;
const float _distRange = 500;
const float _mul = 1.0 / _distRange;
const float _bias = _distOffset * _mul;
_dd = abs(_dd);
_dd *= _dd;
_dd *= saturate( frag_dist * _mul + _bias );
}
curr_col_fog = lerp( FogColorMiddle.xyz, (_dot>0.0f ? FogColorFront.xyz : FogColorBack.xyz), _dd );
curr_col_aerial = lerp( AerialColorMiddle.xyz, (_dot>0.0f ? AerialColorFront.xyz : AerialColorBack.xyz), _dd );
}Этот блок кода чётко даёт нам понять, откуда же взялись эти 0.002 и -0.300. Как мы видим, скалярное произведение между векторами вида и освещения отвечают за выбор между «передним» и «задним» цветами. Умно!
Вот визуализация получившегося итогового градиента (_dd).

Однако вычисление влияния атмосферы/тумана гораздо сложнее. Как видите, у нас гораздо больше параметров, чем просто цвета rgb. В них входят, например, плотность сцены. Мы используем raymarching (16 шагов, и именно поэтому цикл можно развернуть) для определения величины тумана и коэффициента масштаба:
Имея вектор [камера ---> мир], мы можем разделить все его компоненты на 16 — это будет один шаг raymarching-а. Как мы видим ниже, в вычислениях участвует только компонента .z (высота) (curr_pos_z_step).
Подробнее почитать о тумане, реализованном raymarching-ом, можно, например, здесь.
float fog_amount = 1;
float fog_amount_scale = 0;
[branch]
if ( frag_dist >= AerialParams.y )
{
float curr_pos_z_base = (customCameraPos.z + FogBaseParams.y) * density_factor;
float curr_pos_z_step = frag_step.z * density_factor;
[unroll]
for ( int i=16; i>0; --i )
{
fog_amount *= 1 - saturate( density_sample_scale / (1 + max( 0.0, curr_pos_z_base + (i) * curr_pos_z_step ) ) );
}
fog_amount = 1 - fog_amount;
fog_amount_scale = saturate( (frag_dist - AerialParams.y) * AerialParams.z );
}
FogResult ret;
ret.paramsFog = float4 ( curr_col_fog, fog_amount_scale * pow( abs(fog_amount), final_exp_fog ) );
ret.paramsAerial = float4 ( curr_col_aerial, fog_amount_scale * pow( abs(fog_amount), final_exp_aerial ) );Величина тумана очевидно зависит от высоты (компоненты .z), в конце величина тумана возводится в степень тумана/атмосферы.
final_exp_fog and final_exp_aerial берутся из буфера констант; они позволяют управлять тем, как цвета тумана и атмосферы влияют на мир с повышением высоты.
Переопределение тумана
В найденном мной шейдере не было следующего фрагмента ассемблерного кода:
109: mad_sat r1.xy, r0.wwww, cb12[189].xzxx, cb12[189].ywyy
110: add r5.xyz, -r3.xyzx, cb12[188].xyzx
111: mad r5.xyz, r1.xxxx, r5.xyzx, r3.xyzx
112: add r0.z, l(-1.000000), cb12[188].w
113: mad r0.z, r1.y, r0.z, l(1.000000)
114: mul_sat r5.w, r0.w, r0.z
115: lt r0.z, l(0.000000), cb12[192].x
116: if_nz r0.z
117: mad_sat r1.xy, r0.wwww, cb12[191].xzxx, cb12[191].ywyy
118: add r6.xyz, -r3.xyzx, cb12[190].xyzx
119: mad r3.xyz, r1.xxxx, r6.xyzx, r3.xyzx
120: add r0.z, l(-1.000000), cb12[190].w
121: mad r0.z, r1.y, r0.z, l(1.000000)
122: mul_sat r3.w, r0.w, r0.z
123: add r1.xyzw, -r5.xyzw, r3.xyzw
124: mad r5.xyzw, cb12[192].xxxx, r1.xyzw, r5.xyzw
125: endifСудя по тому, что мне удалось понять, это походит на переопределение цвета и влияния тумана:
Большую часть времени выполняется только одно переопределение (cb12_v192.x равно 0.0), но в этом конкретном случае его значение равно ~0.22, поэтому мы выполняем второе переопределение.

#ifdef OVERRIDE_FOG
// Override
float fog_influence = ret.paramsFog.w; // r0.w
float override1ColorScale = cb12_v189.x;
float override1ColorBias = cb12_v189.y;
float3 override1Color = cb12_v188.rgb;
float override1InfluenceScale = cb12_v189.z;
float override1InfluenceBias = cb12_v189.w;
float override1Influence = cb12_v188.w;
float override1ColorAmount = saturate(fog_influence * override1ColorScale + override1ColorBias);
float override1InfluenceAmount = saturate(fog_influence * override1InfluenceScale + override1InfluenceBias);
float4 paramsFogOverride;
paramsFogOverride.rgb = lerp(curr_col_fog, override1Color, override1ColorAmount ); // ***r5.xyz
float param1 = lerp(1.0, override1Influence, override1InfluenceAmount); // r0.x
paramsFogOverride.w = saturate(param1 * fog_influence ); // ** r5.w
const float extraFogOverride = cb12_v192.x;
[branch]
if (extraFogOverride > 0.0)
{
float override2ColorScale = cb12_v191.x;
float override2ColorBias = cb12_v191.y;
float3 override2Color = cb12_v190.rgb;
float override2InfluenceScale = cb12_v191.z;
float override2InfluenceBias = cb12_v191.w;
float override2Influence = cb12_v190.w;
float override2ColorAmount = saturate(fog_influence * override2ColorScale + override2ColorBias);
float override2InfluenceAmount = saturate(fog_influence * override2InfluenceScale + override2InfluenceBias);
float4 paramsFogOverride2;
paramsFogOverride2.rgb = lerp(curr_col_fog, override2Color, override2ColorAmount); // r3.xyz
float ov_param1 = lerp(1.0, override2Influence, override2InfluenceAmount); // r0.z
paramsFogOverride2.w = saturate(ov_param1 * fog_influence); // r3.w
paramsFogOverride = lerp(paramsFogOverride, paramsFogOverride2, extraFogOverride);
}
ret.paramsFog = paramsFogOverride;
#endifВот наша готовая цена без переопределения тумана (первое изображение), с одним переопределением (второе изображение) и двойным переопределением (третье изображение, окончательный результат):



Регулирование ambient occlusion
В найденном мной шейдере также совершенно не использовалось ambient occlusion. Давайте снова взглянем на текстуру AO и на код, который нам интересен:

13: ld_indexable(texture2d)(float,float,float,float) r0.x, r0.xyzw, t2.xyzw
14: max r0.x, r0.x, cb3[1].x
15: add r0.yzw, r1.xxyz, -cb12[0].xxyz
16: dp3 r1.x, r0.yzwy, r0.yzwy
17: sqrt r1.x, r1.x
18: add r1.y, r1.x, -cb3[0].x
19: add r1.zw, -cb3[0].xxxz, cb3[0].yyyw
20: div_sat r1.y, r1.y, r1.z
21: mad r1.y, r1.y, r1.w, cb3[0].z
22: add r0.x, r0.x, l(-1.000000)
23: mad r0.x, r1.y, r0.x, l(1.000000)Возможно, эта сцена — не лучший пример, потому что мы не видим деталей на далёком острове. Тем не менее, давайте взглянем на буфер констант, который используется для задания значения ambient occlusion:

Мы начинаем с загрузки AO из текстуры, затем выполняем инструкцию max. В этой сцене cb3_v1.x очень высоко (0.96888), из-за чего AO становится очень слабым.
Следующая часть кода вычисляет расстояние между позициями камеры и пикселей в мире.
Я считаю, что код иногда говорит сам за себя, поэтому посмотрим на HLSL, выполняющий основную часть этой настройки:
float AdjustAmbientOcclusion(in float inputAO, in float worldToCameraDistance)
{
// *** Inputs *** //
const float aoDistanceStart = cb3_v0.x;
const float aoDistanceEnd = cb3_v0.y;
const float aoStrengthStart = cb3_v0.z;
const float aoStrengthEnd = cb3_v0.w;
// * Adjust AO
float aoDistanceIntensity = linstep( aoDistanceStart, aoDistanceEnd, worldToCameraDistance );
float aoStrength = lerp(aoStrengthStart, aoStrengthEnd, aoDistanceIntensity);
float adjustedAO = lerp(1.0, inputAO, aoStrength);
return adjustedAO;
}Вычисленное расстояние между камерой и миром используется для функции linstep. Мы уже знаем эту функцию, она появлялась в шейдере перистых облаков.
Как вы видите, в буфере констант у нас есть значения расстояний начала/конца AO. Выходные данные linstep влияют на силу AO (а также из cbuffer), а сила влияет на выходящее значение AO.
Краткий пример: пиксель находится далеко, допустим, расстояние равно 500.
linstep возвращает 1.0;
aoStrength равно aoStrengthEnd;
Это приводит к возврату AO, которое составляет примерно 77% (конечная сила) входящего значения.
Входящее AO для этой функции предварительно было подвергнуто операции max.
Соединяем всё вместе
Получив цвет и влияние для цвета тумана и цвета атмосферы, можно их окончательно объединить.
Мы начинаем с ослабления влияния с помощью полученного AO:
...
FogResult fog = CalculateFog( worldPos, CameraPosition, fogStart, ao, false );
// Apply AO to influence
fog.paramsFog.w *= ao;
fog.paramsAerial.w *= ao;
// Mix fog with scene color
outColor = ApplyFog(fog, colorHDR);Вся магия творится в функции ApplyFog:
float3 ApplyFog(FogResult fog, float3 color)
{
const float3 LuminanceFactors = float3(0.333f, 0.555f, 0.222f);
float3 aerialColor = dot(LuminanceFactors, color) * fog.paramsAerial.xyz;
color = lerp(color, aerialColor, fog.paramsAerial.w);
color = lerp(color, fog.paramsFog.xyz, fog.paramsFog.w);
return color.xyz;
}Сначала мы вычисляем «светимость» пикселей:

Затем мы умножаем её на цвет атмосферы:

Затем мы комбинируем HDR-цвет с цветом атмосферы:

Последний этап заключается в комбинировании промежуточного результата с цветом тумана:

Вот и всё!
Несколько отладочных скриншотов

Влияние атмосферы

Цвет атмосферы

Влияние тумана

Цвет тумана

Готовая сцена без тумана

Готовая сцена только с туманом атмосферы

Готовая сцена — только основной туман

Снова готовая сцена со всем туманом для простоты сравнения
Итог
Думаю, вы сможете разобраться во многом изложенном, если взглянете на шейдер, он находится здесь.
С удовольствием могу сказать, что этот шейдер в точности такой же, как оригинальный — это очень меня радует.
В общем случае, готовый результат сильно зависит от значений передаваемых шейдеру. Это не «волшебное» решение, дающее идеальные цвета на выходе, оно требует множества итераций и работы художников, чтобы окончательный результат выглядел достойно. Думаю, это может быть долгий процесс, но после того, как вы его выполните, результат будет очень убедительным, точно как эта закатная сцена.
В шейдере неба «Ведьмака 3» тоже используются вычисления тумана для создания плавного перехода цветов возле горизонта. Однако шейдеру неба передаётся другой набор коэффициентов плотности.
Напомню — бОльшая часть этого шейдера была создана/проанализирована не мной. Все благодарности следует направлять CD PROJEKT RED. Поддержите их, они делают отличную работу.
Часть 3. Падающие звёзды
В «Ведьмаке 3» есть небольшая, но любопытная подробность — падающие звёзды. Интересно, что их, похоже, нет в DLC «Кровь и вино».
В видео можно увидеть, как они выглядят:
Давайте разберёмся, как удалось получить этот эффект.
Как можно заметить, тело падающей звезды намного ярче хвоста. Это важное свойство, которым мы позже воспользуемся.
Наша повестка дня довольно привычна: сначала я опишу общие свойства, затем расскажу о темах, связанных с геометрией, а в конце мы перейдём к пиксельному шейдеру, где творится самое интересное.
1. Общий обзор
Вкратце расскажем о том, что происходит.
Падающие звёзды отрисовываются в упреждающем проходе, сразу после купола неба, неба и луны:
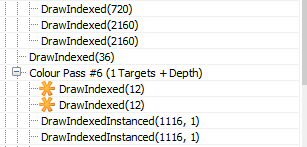
DrawIndexed(720) — купол неба,
DrawIndexed(2160) — сфера для неба/луны,
DrawIndexed(36) — к делу не относится, выглядит как параллелепипед окклюзии солнца (?)
DrawIndexed(12) — падающая звезда
DrawIndexedInstanced(1116, 1) — перистые облака
Аналогично перистым облакам, каждая падающая звезда отрисовывается два раза подряд.

Перед первым вызовом отрисовки

Результат первого вызова отрисовки

Результат второго вызова отрисовки
Кроме того, как и во многих элементах упреждающего прохода этой игры, используется следующее состояние смешивания:

2. Геометрия
С точки зрения геометрии первым делом стоит упомянуть, что каждая падающая звезда представлена тонким четырёхугольником (quad) с texcoords: 4 вершины, 6 индексов. Это самый простейших quad из возможных.
Приближенный quad падающей звезды

Ещё сильнее приближенный quad падающей звезды. Видно каркасное отображение линии, обозначающей два треугольника.
Постойте-ка, но там ведь есть DrawIndexed(12)! Значит ли это, что мы отрисовываем одновременно две падающие звезды?
Да.

В этом кадре одна из падающих звёзд полностью находится вне пирамиды видимости.
Давайте теперь посмотрим на ассемблерный код вершинного шейдера:
vs_5_0
dcl_globalFlags refactoringAllowed
dcl_constantbuffer cb1[9], immediateIndexed
dcl_constantbuffer cb2[3], immediateIndexed
dcl_constantbuffer cb12[193], immediateIndexed
dcl_input v0.xyz
dcl_input v1.xyzw
dcl_input v2.xy
dcl_input v3.xy
dcl_input v4.xy
dcl_input v5.xyz
dcl_input v6.x
dcl_input v7.x
dcl_output o0.xyzw
dcl_output o1.xyzw
dcl_output o2.xy
dcl_output o3.xyzw
dcl_output_siv o4.xyzw, position
dcl_temps 5
0: mov r0.xyz, v0.xyzx
1: mov r0.w, l(1.000000)
2: dp4 r1.x, r0.xyzw, cb2[0].xyzw
3: dp4 r1.y, r0.xyzw, cb2[1].xyzw
4: dp4 r1.z, r0.xyzw, cb2[2].xyzw
5: add r0.x, v2.x, v2.y
6: add r0.y, -v2.y, v2.x
7: add r2.xyz, -r1.zxyz, cb1[8].zxyz
8: dp3 r0.z, r2.xyzx, r2.xyzx
9: rsq r0.z, r0.z
10: mul r2.xyz, r0.zzzz, r2.xyzx
11: dp3 r0.z, v5.xyzx, v5.xyzx
12: rsq r0.z, r0.z
13: mul r3.xyz, r0.zzzz, v5.xyzx
14: mul r4.xyz, r2.xyzx, r3.yzxy
15: mad r2.xyz, r2.zxyz, r3.zxyz, -r4.xyzx
16: dp3 r0.z, r2.xyzx, r2.xyzx
17: rsq r0.z, r0.z
18: mul r2.xyz, r0.zzzz, r2.xyzx
19: mad r0.z, v7.x, v6.x, l(1.000000)
20: mul r3.xyz, r0.zzzz, r3.xyzx
21: mul r3.xyz, r3.xyzx, v3.xxxx
22: mul r2.xyz, r2.xyzx, v3.yyyy
23: mad r0.xzw, r3.xxyz, r0.xxxx, r1.xxyz
24: mad r0.xyz, r2.xyzx, r0.yyyy, r0.xzwx
25: mov r0.w, l(1.000000)
26: dp4 o4.x, r0.xyzw, cb1[0].xyzw
27: dp4 o4.y, r0.xyzw, cb1[1].xyzw
28: dp4 o4.z, r0.xyzw, cb1[2].xyzw
29: dp4 o4.w, r0.xyzw, cb1[3].xyzw
30: add r0.xyz, r0.xyzx, -cb12[0].xyzx
31: dp3 r0.w, r0.xyzx, r0.xyzx
32: sqrt r0.w, r0.w
33: div r0.xyz, r0.xyzx, r0.wwww
34: add r0.w, r0.w, -cb12[22].z
35: max r0.w, r0.w, l(0)
36: min r0.w, r0.w, cb12[42].z
37: dp3 r0.x, cb12[38].xyzx, r0.xyzx
38: mul r0.y, abs(r0.x), abs(r0.x)
39: mad_sat r1.x, r0.w, l(0.002000), l(-0.300000)
40: mul r0.y, r0.y, r1.x
41: lt r1.x, l(0), r0.x
42: movc r1.yzw, r1.xxxx, cb12[39].xxyz, cb12[41].xxyz
43: add r1.yzw, r1.yyzw, -cb12[40].xxyz
44: mad r1.yzw, r0.yyyy, r1.yyzw, cb12[40].xxyz
45: movc r2.xyz, r1.xxxx, cb12[45].xyzx, cb12[47].xyzx
46: add r2.xyz, r2.xyzx, -cb12[46].xyzx
47: mad o0.xyz, r0.yyyy, r2.xyzx, cb12[46].xyzx
48: ge r0.y, r0.w, cb12[48].y
49: if_nz r0.y
50: mad r0.y, r0.z, cb12[22].z, cb12[0].z
51: mul r0.z, r0.w, r0.z
52: mul r0.z, r0.z, l(0.062500)
53: mul r1.x, r0.w, cb12[43].x
54: mul r1.x, r1.x, l(0.062500)
55: add r0.x, r0.x, cb12[42].x
56: add r2.x, cb12[42].x, l(1.000000)
57: div_sat r0.x, r0.x, r2.x
58: add r2.x, -cb12[43].z, cb12[43].y
59: mad r0.x, r0.x, r2.x, cb12[43].z
60: add r0.y, r0.y, cb12[42].y
61: mul r2.x, r0.x, r0.y
62: mul r0.z, r0.x, r0.z
63: mad r3.xyzw, r0.zzzz, l(16.000000, 15.000000, 14.000000, 13.000000), r2.xxxx
64: max r3.xyzw, r3.xyzw, l(0, 0, 0, 0)
65: add r3.xyzw, r3.xyzw, l(1.000000, 1.000000, 1.000000, 1.000000)
66: div_sat r3.xyzw, r1.xxxx, r3.xyzw
67: add r3.xyzw, -r3.xyzw, l(1.000000, 1.000000, 1.000000, 1.000000)
68: mul r2.y, r3.y, r3.x
69: mul r2.y, r3.z, r2.y
70: mul r2.y, r3.w, r2.y
71: mad r3.xyzw, r0.zzzz, l(12.000000, 11.000000, 10.000000, 9.000000), r2.xxxx
72: max r3.xyzw, r3.xyzw, l(0, 0, 0, 0)
73: add r3.xyzw, r3.xyzw, l(1.000000, 1.000000, 1.000000, 1.000000)
74: div_sat r3.xyzw, r1.xxxx, r3.xyzw
75: add r3.xyzw, -r3.xyzw, l(1.000000, 1.000000, 1.000000, 1.000000)
76: mul r2.y, r2.y, r3.x
77: mul r2.y, r3.y, r2.y
78: mul r2.y, r3.z, r2.y
79: mul r2.y, r3.w, r2.y
80: mad r3.xyzw, r0.zzzz, l(8.000000, 7.000000, 6.000000, 5.000000), r2.xxxx
81: max r3.xyzw, r3.xyzw, l(0, 0, 0, 0)
82: add r3.xyzw, r3.xyzw, l(1.000000, 1.000000, 1.000000, 1.000000)
83: div_sat r3.xyzw, r1.xxxx, r3.xyzw
84: add r3.xyzw, -r3.xyzw, l(1.000000, 1.000000, 1.000000, 1.000000)
85: mul r2.y, r2.y, r3.x
86: mul r2.y, r3.y, r2.y
87: mul r2.y, r3.z, r2.y
88: mul r2.y, r3.w, r2.y
89: mad r2.zw, r0.zzzz, l(0.000000, 0.000000, 4.000000, 3.000000), r2.xxxx
90: max r2.zw, r2.zzzw, l(0, 0, 0, 0)
91: add r2.zw, r2.zzzw, l(0.000000, 0.000000, 1.000000, 1.000000)
92: div_sat r2.zw, r1.xxxx, r2.zzzw
93: add r2.zw, -r2.zzzw, l(0.000000, 0.000000, 1.000000, 1.000000)
94: mul r2.y, r2.z, r2.y
95: mul r2.y, r2.w, r2.y
96: mad r2.x, r0.z, l(2.000000), r2.x
97: max r2.x, r2.x, l(0)
98: add r2.x, r2.x, l(1.000000)
99: div_sat r2.x, r1.x, r2.x
100: add r2.x, -r2.x, l(1.000000)
101: mul r2.x, r2.x, r2.y
102: mad r0.x, r0.y, r0.x, r0.z
103: max r0.x, r0.x, l(0)
104: add r0.x, r0.x, l(1.000000)
105: div_sat r0.x, r1.x, r0.x
106: add r0.x, -r0.x, l(1.000000)
107: mad r0.x, -r2.x, r0.x, l(1.000000)
108: add r0.y, r0.w, -cb12[48].y
109: mul_sat r0.y, r0.y, cb12[48].z
110: else
111: mov r0.xy, l(1.000000, 0.000000, 0.000000, 0.000000)
112: endif
113: log r0.x, r0.x
114: mul r0.z, r0.x, cb12[42].w
115: exp r0.z, r0.z
116: mul r0.z, r0.z, r0.y
117: mul r0.x, r0.x, cb12[48].x
118: exp r0.x, r0.x
119: mul o0.w, r0.x, r0.y
120: mad_sat r0.xy, r0.zzzz, cb12[189].xzxx, cb12[189].ywyy
121: add r2.xyz, -r1.yzwy, cb12[188].xyzx
122: mad r2.xyz, r0.xxxx, r2.xyzx, r1.yzwy
123: add r0.x, cb12[188].w, l(-1.000000)
124: mad r0.x, r0.y, r0.x, l(1.000000)
125: mul_sat r2.w, r0.x, r0.z
126: lt r0.x, l(0), cb12[192].x
127: if_nz r0.x
128: mad_sat r0.xy, r0.zzzz, cb12[191].xzxx, cb12[191].ywyy
129: add r3.xyz, -r1.yzwy, cb12[190].xyzx
130: mad r1.xyz, r0.xxxx, r3.xyzx, r1.yzwy
131: add r0.x, cb12[190].w, l(-1.000000)
132: mad r0.x, r0.y, r0.x, l(1.000000)
133: mul_sat r1.w, r0.x, r0.z
134: add r0.xyzw, -r2.xyzw, r1.xyzw
135: mad o1.xyzw, cb12[192].xxxx, r0.xyzw, r2.xyzw
136: else
137: mov o1.xyzw, r2.xyzw
138: endif
139: mov o3.xyzw, v1.xyzw
140: mov o2.xy, v4.yxyy
141: retЗдесь внимание сразу может привлечь вычисление тумана (строки 30-138). Вычисление тумана повершинно имеет смысл из соображений производительности. Кроме того, нам не нужна такая точность тумана — метеороиды обычно пролетают над головой Геральта и не достигают горизонта.
Параметры атмосферы (rgb = цвет, a = влияние) сохраняются в o0.xyzw, а параметры тумана в o1.xyzw.
o2.xy (строка 140) — это просто texcoords.
o3.xyzw (строка 139) к делу не относится.
Теперь скажем несколько слов о вычислении позиции в мире. Вершинные шейдеры выполняют билбординг. В первую очередь входящие данные для билбордов поступают из вершинного буфера — давайте взглянем на них.
Первые данные — это Position (позиция):
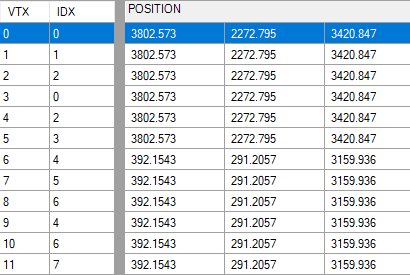
Как было сказано выше, здесь у нас 2 quad-а: 8 вершин, 12 индексов.
Но почему для каждого quad-а позиция одинакова? Всё довольно просто — это позиция центра quad-а.
Далее,, у каждой вершины есть смещение от центра к краю quad-а:
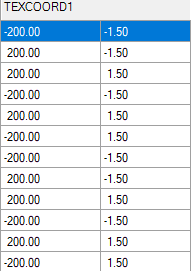
Это означает, что каждая падающая звезда имеет в мировом пространстве размер (400, 3) единиц. (на плоскости XY, в Witcher 3 ось Z направлена вверх)
Последний элемент, который есть у каждой вершины — это единичный вектор направления в мировом пространстве, управляющий движением падающей звезды:
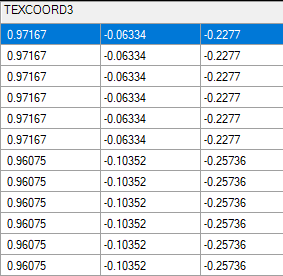
Так как данные поступают от ЦП, сложно понять, как они вычисляются.
Теперь перейдём к коду билбординга. Идея достаточно проста — сначала получается единичный вектор от центра quad-а до камеры:
7: add r2.xyz, -r1.zxyz, cb1[8].zxyz
8: dp3 r0.z, r2.xyzx, r2.xyzx
9: rsq r0.z, r0.z
10: mul r2.xyz, r0.zzzz, r2.xyzxЗатем получается единичный касательный вектор, управляющий движением падающей звезды.
Учитывая, что этот вектор уже нормализован на стороне ЦП, эта нормализация избыточна.
11: dp3 r0.z, v5.xyzx, v5.xyzx
12: rsq r0.z, r0.z
13: mul r3.xyz, r0.zzzz, v5.xyzxПри наличии двух векторов используется векторное произведение для определения вектора бикасательной, перпендикулярного обоим входящим векторам.
14: mul r4.xyz, r2.xyzx, r3.yzxy
15: mad r2.xyz, r2.zxyz, r3.zxyz, -r4.xyzx
16: dp3 r0.z, r2.xyzx, r2.xyzx
17: rsq r0.z, r0.z
18: mul r2.xyz, r0.zzzz, r2.xyzxТеперь у нас есть нормализованные векторы касательной(r3.xyz) и бикасательной (r2.xyz).
Давайте введём Xsize и Ysize, соответствующие входящему элементу TEXCOORD1, поэтому например (-200, 1.50).
Окончательное вычисление позиции в мировом пространстве выполняется так:
19: mad r0.z, v7.x, v6.x, l(1.000000)
20: mul r3.xyz, r0.zzzz, r3.xyzx
21: mul r3.xyz, r3.xyzx, v3.xxxx
22: mul r2.xyz, r2.xyzx, v3.yyyy
23: mad r0.xzw, r3.xxyz, r0.xxxx, r1.xxyz
24: mad r0.xyz, r2.xyzx, r0.yyyy, r0.xzwx
25: mov r0.w, l(1.000000) Учитывая то, что r0.x, r0.y и r0.z равны 1.0, окончательное вычисление упрощается:
worldSpacePosition = quadCenter + tangent * Xsize + bitangent * Ysize
Последняя часть — это простое умножение позиции в мировом пространстве на матрицу «вид-проекция» для получения SV_Position:
26: dp4 o4.x, r0.xyzw, cb1[0].xyzw
27: dp4 o4.y, r0.xyzw, cb1[1].xyzw
28: dp4 o4.z, r0.xyzw, cb1[2].xyzw
29: dp4 o4.w, r0.xyzw, cb1[3].xyzw 3. Пиксельный шейдер
Как сказано в разделе «Общий обзор», используется следующее состояние смешивания:
FinalColor = SrcColor * One + DestColor * (1.0 - SrcAlpha) =
FinalColor = SrcColor + DestColor * (1.0 - SrcAlpha)
где SrcColorи SrcAlpha — это, соответственно, компоненты .rgb и .a из пиксельного шейдера, а DestColor цвет .rgb, в текущий момент находящийся в rendertarget.
Основной показатель, управляющий прозрачностью — это SrcAlpha. Многие упреждающие шейдеры игры вычисляют его как непрозрачность (opacity) и применяют его в конце следующим образом:
return float4( color * opacity, opacity )
Шейдер падающих звёзд не стал исключением. Следуя этому шаблону, рассмотрим три случая, в которых opacity равно 1.0, 0.1 и 0.0.
a) opacity = 1.0
FinalColor = color * opacity + DestColor * (1.0 - opacity) =
FinalColor = color = SrcColor

b) opacity = 0.1
FinalColor = color * opacity + DestColor * (1.0 - opacity) =
FinalColor = 0.1 * color + 0.9 * DestColor

c) opacity = 0.0
FinalColor = color * opacity + DestColor * (1.0 - opacity) =
FinalColor = DestColor

Основополагающая идея этого шейдера заключается в моделировании и использовании функции непрозрачности opacity(x), которая управляет непрозрачностью пикселя вдоль падающей звезды. Основное требование — непрозрачность должна достигать максимальных значений на конце звезды (её «теле») и плавно затухать до 0.0 (к её «хвосту»).
Когда мы начинаем разбираться с ассемблерным кодом пиксельного шейдера, это становится очевидно:
ps_5_0
dcl_globalFlags refactoringAllowed
dcl_constantbuffer cb0[10], immediateIndexed
dcl_constantbuffer cb2[3], immediateIndexed
dcl_constantbuffer cb4[2], immediateIndexed
dcl_input_ps linear v0.xyzw
dcl_input_ps linear v1.xyzw
dcl_input_ps linear v2.y
dcl_input_ps linear v3.w
dcl_output o0.xyzw
dcl_temps 4
0: mov_sat r0.x, v2.y
1: ge r0.y, r0.x, l(0.052579)
2: ge r0.z, l(0.965679), r0.x
3: and r0.y, r0.z, r0.y
4: if_nz r0.y
5: ge r0.y, l(0.878136), r0.x
6: add r0.z, r0.x, l(-0.052579)
7: mul r1.w, r0.z, l(1.211303)
8: mov_sat r0.z, r1.w
9: mad r0.w, r0.z, l(-2.000000), l(3.000000)
10: mul r0.z, r0.z, r0.z
11: mul r0.z, r0.z, r0.w
12: mul r2.x, r0.z, l(0.084642)
13: mov r1.yz, l(0.000000, 0.000000, 0.084642, 0.000000)
14: movc r2.yzw, r0.yyyy, r1.yyzw, l(0.000000, 0.000000, 0.000000, 0.500000)
15: not r0.z, r0.y
16: if_z r0.y
17: ge r0.y, l(0.924339), r0.x
18: add r0.w, r0.x, l(-0.878136)
19: mul r1.w, r0.w, l(21.643608)
20: mov_sat r0.w, r1.w
21: mad r3.x, r0.w, l(-2.000000), l(3.000000)
22: mul r0.w, r0.w, r0.w
23: mul r0.w, r0.w, r3.x
24: mad r1.x, r0.w, l(0.889658), l(0.084642)
25: mov r1.yz, l(0.000000, 0.084642, 0.974300, 0.000000)
26: movc r2.xyzw, r0.yyyy, r1.xyzw, r2.xyzw
27: else
28: mov r2.y, l(0)
29: mov r0.y, l(-1)
30: endif
31: not r0.w, r0.y
32: and r0.z, r0.w, r0.z
33: if_nz r0.z
34: ge r0.y, r0.x, l(0.924339)
35: add r0.x, r0.x, l(-0.924339)
36: mul r1.w, r0.x, l(24.189651)
37: mov_sat r0.x, r1.w
38: mad r0.z, r0.x, l(-2.000000), l(3.000000)
39: mul r0.x, r0.x, r0.x
40: mul r0.x, r0.x, r0.z
41: mad r1.x, r0.x, l(-0.974300), l(0.974300)
42: mov r1.yz, l(0.000000, 0.974300, 0.000000, 0.000000)
43: movc r2.xyzw, r0.yyyy, r1.xyzw, r2.xyzw
44: endif
45: else
46: mov r2.yzw, l(0.000000, 0.000000, 0.000000, 0.500000)
47: mov r0.y, l(0)
48: endif
49: mov_sat r2.w, r2.w
50: mad r0.x, r2.w, l(-2.000000), l(3.000000)
51: mul r0.z, r2.w, r2.w
52: mul r0.x, r0.z, r0.x
53: add r0.z, -r2.y, r2.z
54: mad r0.x, r0.x, r0.z, r2.y
55: movc r0.x, r0.y, r2.x, r0.x
56: mad r0.y, cb4[1].x, -cb0[9].w, l(1.000000)
57: mul_sat r0.y, r0.y, v3.w
58: mul r0.x, r0.y, r0.x
59: mul r0.yzw, cb2[2].xxyz, cb4[0].xxxx
60: mul r0.x, r0.x, cb2[2].w
61: dp3 r1.x, l(0.333000, 0.555000, 0.222000, 0.000000), r0.yzwy
62: mad r1.xyz, r1.xxxx, v0.xyzx, -r0.yzwy
63: mad r0.yzw, v0.wwww, r1.xxyz, r0.yyzw
64: add r1.xyz, -r0.yzwy, v1.xyzx
65: mad r0.yzw, v1.wwww, r1.xxyz, r0.yyzw
66: mul o0.xyz, r0.xxxx, r0.yzwy
67: mov o0.w, r0.x
68: retВ общем случае, шейдер немного переусложнён и мне трудно было разобраться, что в нём происходит. Например, откуда взялись все значения наподобие 1.211303, 21.643608 и 24.189651?
Если мы говорим о функции непрозрачности, то нам нужно одно входящее значение. С этим довольно просто — здесь полезна будет texcoord в интервале от [0,1] (строка 0), чтобы мы могли применить функцию к всей длине метеороида.
Функция непрозрачности имеет три сегмента/интервала, определяемых с помощью четырёх контрольных точек:
// current status: no idea how these are generated
const float controlPoint0 = 0.052579;
const float controlPoint1 = 0.878136;
const float controlPoint2 = 0.924339;
const float controlPoint3 = 0.965679;Понятия не имею, как их подбирали/вычисляли.
Как мы видим из ассемблерного кода, первое условие — это просто проверка, находится ли входящее значение в интервале [controlPoint0 — controlPoint3]. Если нет, то непрозрачность просто равна 0.0.
// Input for the opacity function
float y = saturate(Input.Texcoords.y); // r0.x
// Value of opacity function.
// 0 - no change
// 1 - full color
float opacity = 0.0;
[branch]
if (y >= controlPoint0 && y <= controlPoint3)
{
...Расшифровка представленного ниже ассемблерного кода необходима, если мы хотим разобраться, как работает функция непрозрачности:
6: add r0.z, r0.x, l(-0.052579)
7: mul r1.w, r0.z, l(1.211303)
8: mov_sat r0.z, r1.w
9: mad r0.w, r0.z, l(-2.000000), l(3.000000)
10: mul r0.z, r0.z, r0.z
11: mul r0.z, r0.z, r0.w
12: mul r2.x, r0.z, l(0.084642)В строке 9 есть коэффициенты '-2.0' и '3.0', что намекает нам об использовании функции smoothstep. Да, это неплохая догадка.
Функция smoothstep языка HLSL с prototype:ret smoothstep(min, max, x) всегда ограничивает x интервалом [min-max]. С точки зрения ассемблера, это вычитает min из входящего значения (то есть из r0.z в строке 9), но ничего подобного в коде нет. Для max это подзразумевает умножение входящего значения, но в коде нет ничего наподобие 'mul_sat'. Вместо этого есть 'mov_sat'. Это подсказывает нам, что min и max функции smoothstep равны 0 и 1.
Теперь мы знаем, что x должен находиться в интервале [0, 1]. Как сказано выше, в функции непрозрачности есть три сегмента. Это явно намекает что код ищет, где мы находимся в интервале [segmentStart-segmentEnd].
Ответом является функция Linstep!
float linstep(float min, float max, float v)
{
return ( (v-min) / (max-min) );
}Например, давайте возьмём первый сегмент: [0.052579 - 0.878136]. Вычитание находится в строке 6. Если мы заменим деление умножением -> 1.0 / (0.878136 — 0.052579) = 1.0 / 0.825557 = ~1.211303.
Результат smoothstep находится в интервале [0, 1]. Умножение в строке 12 — это вес сегмента. Каждый сегмент имеет свой вес, позволяющий управлять максимальной непрозрачностью этого конкретного сегмента.
Это значит, что для первого сегмента [0.052579 — 0.878136] непрозрачность находится в интервале [0 — 0.084642].
Функцию HLSL, вычисляющую непрозрачность для произвольного сегмента, может быть записана следующим образом:
float getOpacityFunctionValue(float x, float cpLeft, float cpRight, float weight)
{
float val = smoothstep( 0, 1, linstep(cpLeft, cpRight, x) );
return val * weight;
}Итак, весь смысл заключается просто в вызове этой функции для соответствующего сегмента.
Взглянем на веса:
const float weight0 = 0.084642;
const float weight1 = 0.889658;
const float weight2 = 0.974300; // note: weight0+weight1 = weight2Согласно ассемблерному коду, функция opacity(x) вычисляется следующим образом:
float opacity = 0.0;
[branch]
if (y >= controlPoint0 && y <= controlPoint3)
{
// Range of v: [0, weight0]
float v = getOpacityFunctionValue(y, controlPoint0, controlPoint1, weight0);
opacity = v;
[branch]
if ( y >= controlPoint1 )
{
// Range of v: [0, weight1]
float v = getOpacityFunctionValue(y, controlPoint1, controlPoint2, weight1);
opacity = weight0 + v;
[branch]
if (y >= controlPoint2)
{
// Range of v: [0, weight2]
float v = getOpacityFunctionValue(y, controlPoint2, controlPoint3, weight2);
opacity = weight2 - v;
}
}
}Вот график функции непрозрачности. Легко можно заметить резкое повышение непрозрачности, обозначающее начало тела падающей звезды:
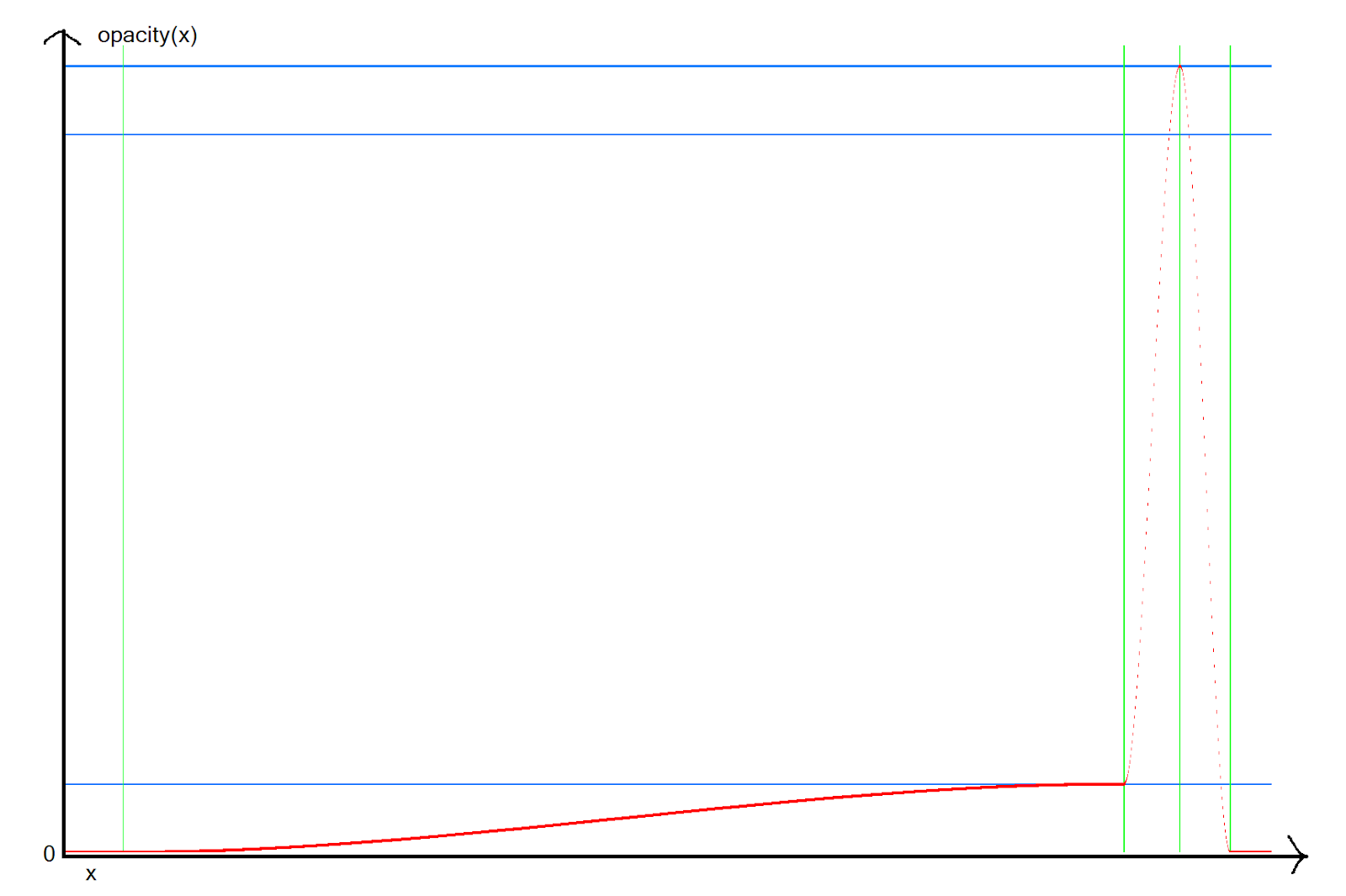
График функции непрозрачности.
Красный канал — значение непрозрачности
Зелёный канал — контрольные точки
Синий канал — веса
После вычисления непрозрачности, всё остальное — просто финальные штрихи. Затем идут дополнительные умножения: непрозрачность звёзд, цвет падающей звезды и влияние тумана. Как обычно в шейдерах TW3, здесь также можно найти избыточные умножения на 1.0:
// cb4_v1.x = 1.0
float starsOpacity = 1.0 - cb0_v9.w * cb4_v1.x;
opacity *= starsOpacity;
// Calculate color of a shooting star
// cb4_v0.x = 10.0
// cb2_v2.rgb = (1.0, 1.0, 1.0)
float3 color = cb2_v2.rgb * cb4_v0.x;
// cb2_v2.w = 1
opacity *= cb2_v2.w;
FogResult fr = { Input.FogParams, Input.AerialParams };
color = ApplyFog(fr, color);
return float4( color*opacity, opacity);
}4. Итог
Основная сложность заключается в части с функцией непрозрачности. После её расшифровки всё остальное понять довольно просто.
Выше я говорил, что пиксельный шейдер немного переусложнён. На самом деле нам важно только значение функции opacity(x), которое хранится в r2.x (начиная со строки 49). Однако функция непрозрачности в ассемблерном коде создаёт ещё три дополнительные переменные: minRange (r2.y), maxRange (r2.z) и value (r2.w). Все они являются параметрами, используемыми для вычисления непрозрачности, когда opacity(x) не используется:
lerp( minRange, maxRange, smoothstep(0, 1, value) );
На самом деле, окончательное значение непрозрачности получается в условном переходе в строке 55 — если входящее значение x находится в интервале [controlPoint0 — controlPoint3], то это означает, что используется функция непрозрачности, поэтому выбирается r2.x. В противном случае, когда x находится за пределами интервала, непрозрачность вычисляется из r0.x, то есть, по приведённому выше уравнению.
Я выполнял отладку нескольких пикселей за пределами интервала [controlPoint0 — controlPoint3], и окончательная непрозрачность всегда оказывалась равной нулю.
Вот и всё на сегодня. И, как всегда, спасибо за прочтение.
Автор: PatientZero