В статье описывается способ сделать для компьютерных игр гексагональную карту (из шестиугольников), покрывающую всю сферическую Землю, чтобы можно было ходить кругосветно не только по экватору, но и через полюса. Возможно, статья заинтересует инди-разработчиков игр.
Введение
Во многих компьютерных играх жанра «стратегия» игровое поле разделено на ячейки, в которые можно помещать юниты, строить сооружения, базы и т.п. Часто ячейка имеет форму квадрата. Если поле описывает поверхность планеты или ее части, содержит горы, реки, океаны, то поле является аналогом географической карты. Поэтому далее будет использоваться термин карта.
Сложности возникают, когда карта представляет собой поверхность всей планеты целиком. На карте не должно быть границ, за которые нельзя выйти. Если игрок долго двигается в одном направлении, он должен вернуться в исходную точку. Чтобы это реализовать, некоторые карты делают цилиндрическими. На них можно ходить вокруг Земли вдоль экватора и вернуться в исходную точку, но выйти за северную и южную границы нельзя. Такая карта не очень соответствует круглой Земле. В некоторых картах выйдя за правую границу игрок оказывается слева, а выйдя за верхнюю границу — снизу. Как говорят математики, карта имеет топологию тора. Она тоже не соответствует круглой Земле. В некоторых играх натягивают цилиндр на глобус. Выйдя за границу широты полюса игрок оказывается на той же широте, но с другой стороны Земли. Такая идея соответствует круглой Земле, но карта получается сильно искаженной. Сравните размеры ячеек возле экватора и возле полюса на рис. 1.

Другой способ минимизировать искажения заключается в натягивании куба на глобус. Карта представляет собой развертку куба. Искажения также присутствуют, наиболее выражены возле углов куба, но не так сильно, как в случае с цилиндром (рис. 2).

Еще один способ минимизировать искажения заключается в использовании гексагональной карты, где ячейка имеет форму шестиугольника (рис. 3). Гексагональные карты тоже распространены в компьютерных играх и описаны, например, здесь, здесь.

Карты с треугольными ячейками
Прежде чем делать гексагональные карты, научимся делать карты с треугольными ячейками. Рассмотрим икосаэдр (рис. 4).

Поверхность фигуры состоит из равносторонних треугольников. Разделим каждую сторону треугольника на N равных частей. Тогда сам треугольник можно разделись на N² маленьких равносторонних треугольников. Вершина каждого маленького треугольника расположена на плоскости грани. Построим вектор, идущий из центра фигуры через вершину на плоскости грани до поверхности сферы, описанной вокруг икосаэдра (рис. 5).

Спроецировав так каждый маленький треугольник, можно получить фигуру, похожую на сферу (рис. 6). В такой фигуре треугольники не будут строго равносторонними, но все равно красиво.

В качестве основы для построения карты для такой фигуры можно использовать развертку икосаэдра, которая состоит из пяти параллелограммов 2:1 (рис. 7). Далее для простоты назовем их листами. Лист состоит из четырех треугольников.

Каждую сторону треугольника разобьем на N частей. Например, при N=2 получится следующее (рис. 8):

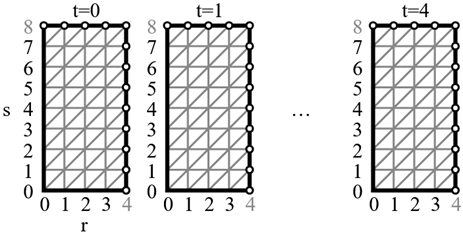
Немного исказим каждый лист, чтобы он стал прямоугольным. Для N=4 пример на рис. 9. Полученная фигура может использоваться как карта. Каждая точка на ней имеет координаты (r, s, t), где t — номер листа (0 ≤ t < 5), s — номер строки на листе (0 ≤ s < 2N), r — номер колонки (0 ≤ r < N). Отдельно располагаются вершины (r=N, s=0) и (r=0, s=2N). Они соответствуют южному и северному полюсу. Им не хватило место на листах, их нужно хранить отдельно. Далее координаты вершин r, s, t будем называть прямоугольными, а координаты x, y, z этих вершин в 3D пространстве — пространственными.
Как рассчитать пространственные координаты
Для этого предлагается пара функций на языке JavaScript и библиотека для работы с векторами, к которой есть документация, если кому интересно.
/** Вычисляет 3D координаты путем продолжения точки с треугольника икосаэдра
* на сферу
* @param {any} N на сколько частей разбиение
* @param {any} r столбец, 0 ≤ r ≤ N
* @param {any} s строка, 0 ≤ s ≤ 2N
* @param {any} t лист, 0 ≤ t < 5
*/
static normal(N, r, s, t) {
const φ = (1 + Math.sqrt(5)) / 2; // золотое сечение
const α = Math.PI / 2 - 2 * Math.atan(1 / φ); // ~ 26,6°
let β = 2 * Math.PI / 5; // 72°
let i, j, v0, v1, v2,
result = vec3.create(),
center = vec3.create();
if (s <= r) {
v0 = vec3.fromAngles(-α, 0);
v1 = vec3.fromValues(0, -1, 0);
v2 = vec3.fromAngles(-α, β);
i = s;
j = r - s;
} else if (s <= N) {
v0 = vec3.fromAngles(-α, 0);
v1 = vec3.fromAngles(α, β / 2);
v2 = vec3.fromAngles(-α, β);
i = r;
j = s - r;
} else if (s <= r + N) {
v0 = vec3.fromAngles(α, β / 2);
v1 = vec3.fromAngles(-α, β);
v2 = vec3.fromAngles(α, 3 * β / 2);
i = s - N;
j = r - s + N;
} else {
v0 = vec3.fromAngles(α, β / 2);
v1 = vec3.fromValues(0, 1, 0);
v2 = vec3.fromAngles(α, 3 * β / 2);
i = r;
j = s - r - N;
}
i /= N;
j /= N;
for (let k = 0; k < 3; k++)
result[k] = (1 - i - j) * v0[k] + j * v1[k] + i * v2[k];
vec3.rotateY(result, result, center, t * β);
vec3.normalize(result, result);
return result;
}
/** Create vec3 from geocoords
* @param {number} φ latitude
* @param {number} θ longitude
*/
vec3.fromAngles = (φ, θ) => vec3.fromValues(
Math.cos(φ) * Math.cos(θ),
Math.sin(φ),
-Math.cos(φ) * Math.sin(θ)
);Для поиска соседних вершин при такой схеме удобно использовать курсор (шесть красных стрелочек), перемещая его по вершинам на листе (рис. 10).

Внутри листа соседи находятся легко. На границе листа нужно учитывать склейку с другими листами. Рассмотрим пример склейки листов при N=4, представленный на рис. 11.

Центр курсора находится в точке (r=0, s=1). Соседними вершинами из этого же листа являются (r=0, s=2), (r=1, s=2), (r=1, s=1) и (r=0, s=0). Еще две стрелочки указывают за границы листа: (r=-1, s=0), (r=-1, s=1). С учетом склейки получается, что они указывают на вершины (r=3, s=4), (r=3, s=5) из листа слева. Полная схема склеек для N=4 представлена на рис. 12.

В двух случаях на листе соседом является полюс (северный или южный, зеленые стрелки). Еще в двух случаях две разных стрелки курсора приводят к одному соседу (синие стрелки). Это наблюдается у вершин (r=0, s=0) и (r=0, s=N), у которых только пять соседей.
Функция для поиска соседей с учетом склеек
/** Возвращает узел по его прямоугольным координатам.
* Координаты могут на единицу отличаться от нормированных, что используется
* для поиска соседей узлов, т.е. -1 ≤ s ≤ 2N, -1 ≤ r ≤ N.
* @param {int} r 0 ≤ r ≤ N
* @param {int} s 0 ≤ s ≤ 2N
* @param {int} t 0 ≤ t < 5
*/
byCoords(r, s, t) {
const N = this.N;
if (r == -1) {
if (s < N) {
t--;
r += N;
s += N;
} else if (s == N && N == 1)
return this.nord;
else {
t--;
r = 2 * N - s - 1;
s = 2 * N - 1;
}
} else if (r == N) {
if (s == 0)
return this.south;
else if (s < N) {
t++;
r = N - s;
s = 0;
} else {
t++;
r -= N;
s -= N;
}
} else if (s == -1) {
if (r == 0 && N == 1)
return this.south;
else {
t--;
s = N - r - 1;
r = N - 1;
}
} else if (s == 2 * N) {
if (r == 0)
return this.nord;
else {
t++;
s = 2 * N - r;
r = 0;
}
}
if (t == -1)
t = 4;
else if (t == 5)
t = 0;
return this.map[t][s][r];
}Гексагональные карты
Назовем вершины треугольников из предыдущего пункта узлами. Поскольку каждый узел граничит с пятью или шестью соседями, вокруг него можно построить пяти или шестиугольник (далее — грань). На рис. 13 синими точками отмечены узлы. Черные линии являются границами граней.

Построив такие грани вокруг каждого из узлов, получим фигуру, похожую на шар и известную как многогранник Гольдберга (рис. 14).

Его поверхность состоит из 12 пятиугольников (всегда) и некоторого количества шестиугольников (зависит от выбранного N). Возможно, меня поправят и скажут, что многогранник Гольдберга, это немного другое, но я просто обязан его здесь упомянуть. Есть ссылка на Youtube. На самом деле многогранников Гольберга больше. Но не для всех из них можно построить простую схему с прямоугольными координатами. Как и в предыдущем пункте с треугольными гранями, грани также имеют разные размеры, разные расстояния до центра фигуры (см. стр. 40), но все равно фигуры смотрятся красиво.
Как построить грань вокруг узла. На карте каждая вершина грани находится в центре треугольника, образованного узлом и двумя его соседями, которые так же являются соседями друг с другом (рис. 15). Можно легко найти пространственные координаты центра треугольника, как среднее арифметическое пространственных координат вершин, и спроецировать на описанную сферу, т.е. нормировать координаты. Соединив все шесть точек вокруг узла по кругу, получим требуемый шестиугольник. На самом деле у автора часто получалось, что вершины немного разбросаны выше и ниже плоскости грани. Возможно, Стэн Шейн здесь был прав, когда говорил, что грани не плоские.

Высоты
Для решения проблемы неплоских поверхностей, но в первую очередь для придания разнообразия карте предлагается добавить каждому узлу числовое свойство высота, расстояние от центра сферы. Пусть на рис. 16 точки A, B (остальные четыре точки шестиугольника опустим) — середины треугольников с соседями из предыдущего пункта. Координаты узла (точка N) по своей сути является вектором нормали к поверхности грани. Возьмем вектор OA и продлим его так, чтобы длина стала равна высоте узла. Получим точку A’. Зная ее и вектор нормали, получим уравнение плоскости, в которой находится грань (составить уравнение плоскости по точке и вектору нормали). Для остальных пяти точек, например, для точки B, можно составить уравнение прямой в параметрическом виде и найти соответствующую точку B’ на плоскости (пересечение плоскости с прямой, заданной параметрически). Получив все шесть точек на плоскости, нарисуем грань.

Высоту узла не следует приравнивать к расстоянию от центра сферы до центра грани, потому что тогда получаются неровные карты. Это наглядно проявляется в форме шестиугольников вокруг пятиугольника на следующем рис. 17. Слева центры граней равноудалены от центра сферы. Справа вершины равноудалены от центра. Шестиугольник слева имеет «более разные» длины сторон.

Нарисовав плоскую грань, добавим ей четырехугольную стенку с соседней гранью. Для этого возьмем две точки грани на плоскости узла и две точки грани на плоскости соседа. Построенная таким образом фигура приобретает дополнительный объем. Разукрасив шестиугольники в разные цвета, можно получить привлекательные карты для игр (рис. 18).

Покрутить карты можно здесь, а исходный код есть на Github.
Спасибо за внимание!
Автор: Konstantin-2






