ChipWhisperer: атака по энергопотреблению на Магму

Автор статьи: rakf

В рамках Summer of Hack 2019 в Digital Security я разбирался с атакой по энергопотреблению и работал с ChipWhisperer.

Что это?

Анализ энергопотребления — это один из видов атак по сторонним каналам. То есть атак, использующих информацию, которая появляется в результате физической реализации системы.

Какая информация может быть полезна атакующему:

• время выполнения криптопреобразований;
• энергопотребление;
• электромагнитные поля;
• шум и т.д.

Атака по энергопотреблению считается наиболее универсальной.

Почему работает?

В основе микропроцессоров, микроконтроллеров, RAM и многих других логических схем лежит технология КМОП (CMOS). Потребляемая мощность КМОП-схем состоит из двух составляющих: статической и динамической. Статическое энергопотребление очень мало, что является одной из причин монополизации технологии. Динамическая мощность обусловлена переключением транзисторов и зависит от обрабатываемых данных и выполняемых операций. Поскольку статическая составляющая в основном постоянна, изменение общей мощности обусловлено исключительно динамической мощностью и, следовательно, общее энергопотребление может быть использовано для анализа.

Инструментарий

ChipWhisperer, я использовал версию с 2 частями:

ChipWhisperer – это набор инструментов с открытым исходным кодом для исследования безопасности embedded устройств. Он позволяет проводить анализ энергопотребления и атаки на основе ошибок.

Плата обойдется в $250. Разработчики позиционируют ее как революционное решение, ведь подобные комплексы, по заявлению создателей, стоят от $30k. Устройство состоит из 2 плат: целевой и платы захвата.

Существуют и другие версии, со своими преимуществами (но и за большую стоимость), также можно отдельно приобрести различные целевые платы, платы расширения, probe для полноценного анализа уже своих устройств и использования ChipWhisperer только для снятия.

У ChipWhisperer есть отличная вики, небольшие лабы для освоения, а к 5 версии даже сделали хорошую документацию по API. Трассы снимаются с подключенного устройства с помощью их ПО и записываются как NumPy массив.

Для начала необходимо написать прошивку для целевого устройства. В рамках лаб рассматриваются шифры AES, DES, TEA. Для них есть уже готовые прошивки и настройки для снятия трасс (количество отсчетов для снятия, смещение, частоту АЦП и др.). Для самостоятельного исследования настройки придется подбирать экспериментально.

Как уже сказано выше, можно спровоцировать сбой целевой платы: вызывая неисправности тактового сигнала, пропускать инструкции и извлекать секретную информацию.

В больших комплексах для снятия трасс используют осциллограф.

Анализ

Существует несколько основных методов анализа:

• простой анализ мощности(SPA);
• дифференциальный анализ мощности(DPA);
• корреляционный анализ мощности(CPA).

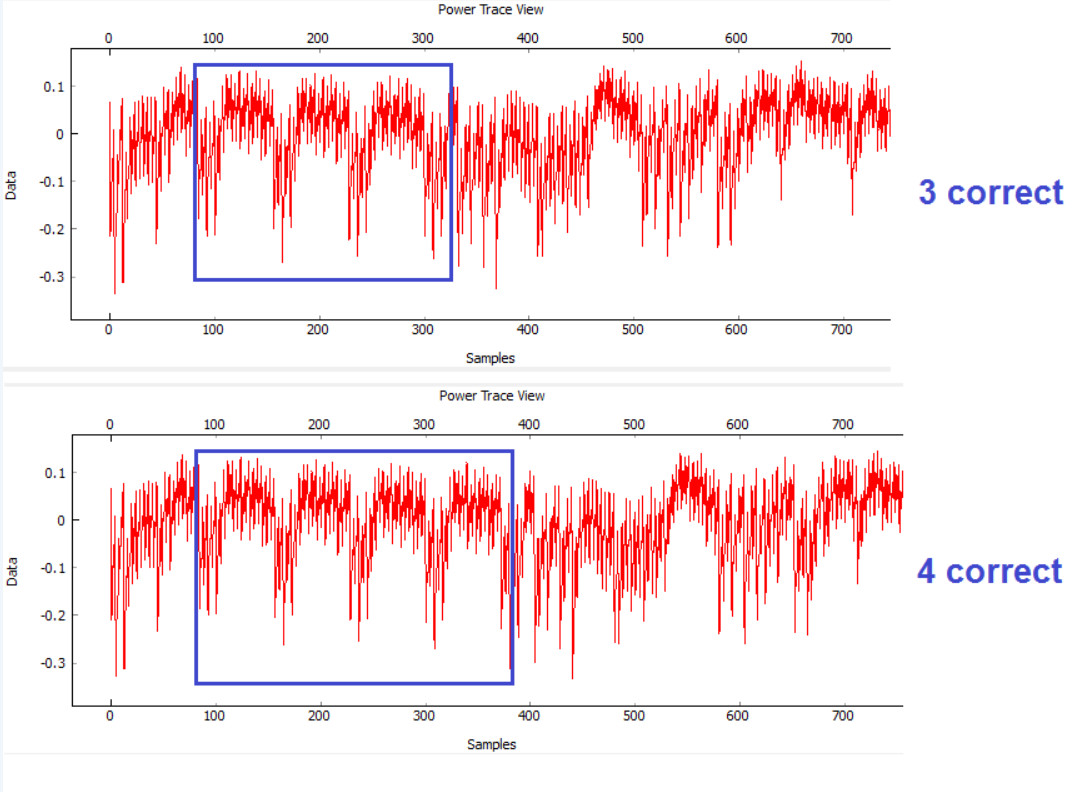
Простой анализ мощности включает в себя визуальный анализ графика энергопотребления. Например, пароль можно получить по одному символу за раз, наблюдая профиль мощности, когда введен правильный символ, и сравнивая с неправильным.

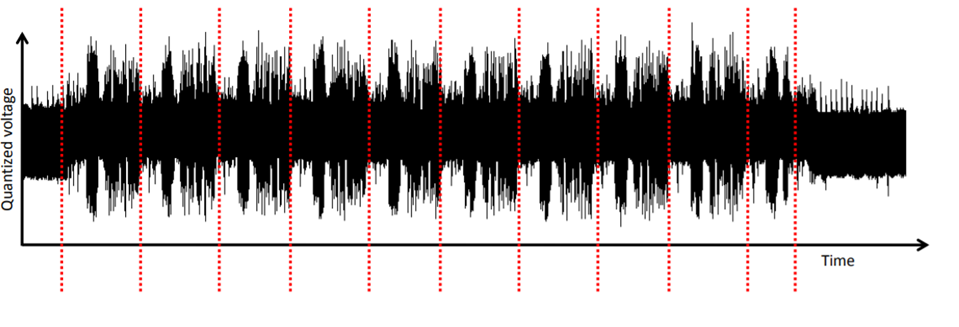
Или можно увидеть раунды шифрования на трассах. Для получения ключа данных мало, но можно предположить, какой алгоритм выполняется. На рисунке отчетливо видно 10 ранудов AES.

Дифференциальный анализ (DPA) гораздо эффективнее простого анализа.DPA основан на методах статистического анализа для выявления различий в следах мощности. Очень действенный инструмент, правда, для "открытия" ключа потребуется большое количество трасс. Этот метод я не использовал для анализа, но в конце дам несколько ссылок на источники, где он хорошо описан.

В основе корреляционного анализа – статистический аппарат для определения секретного ключа шифрования. Иногда его выделяют в отдельный тип, иногда относят к DPA. Этот метод требует меньшего количества трасс, чем DPA, я использовал его для анализа мощности. Расскажу о нем подробнее.

Основной задачей является построение точной модели энергопотребления исследуемого устройства. Если построена точная модель, наблюдается заметная корреляция между прогнозируемым и фактическим значением.

Одна из моделей мощности, которая может быть использована – модель веса Хэмминга. Вес Хэмминга – это количество ненулевых значений в двоичном представлении. Предположение этой модели в том, что количество битов, устанавливаемых в регистре, будет коррелировать с потребляемой устройством энергией. Сам вес Хэмминга используется в дальнейшем как условная единица энергии. Также используется модель расстояния Хэмминга — количество различных битов в 2 значениях.

Для сравнения модели веса Хэмминга и реального энергопотребления используется линейный коэффициент Пирсона. Он показывает линейную зависимость одной величины от другой. При правильно построенной модели данный коэффициент будет стремиться к 1.

Обобщенный алгоритм CPA состоит из следующих основных шагов:

• снимаем энергопотребление при преобразовании сообщений на неизвестном ключе;
• строим модель энергопотребления чипа при преобразовании тех же сообщений на всех возможных вариантах подблока ключа (256 вариантов для каждого байта);
• находим коэффициент линейной корреляции для моделируемого энергопотребления и реального. В случае истинного ключа коэффициент будет стремиться к 1;
• алгоритм повторяется для остальных подблоков ключа.

В итоге ключ восстанавливается последовательно, по небольшим частям. Если атакуем один байт ключа за раз, то используем 2 ⁸ попыток для каждого ключа. Например, если ковырять AES — 128, то общее количество попыток для 16 байт ключа будет 2¹², что намного лучше, чем бить в упор 2¹²⁸.

Анализ шифра Магма

Магма – это шифр, который определен в ГОСТ Р 34.12-2015, по факту тот же самый ГОСТ 28147-89, только в профиль. Шифруемый блок проходит 32 раунда, в которых происходят некоторые преобразования. Ключ состоит из 256 бит, каждый раундовый ключ представляет собой часть исходного.

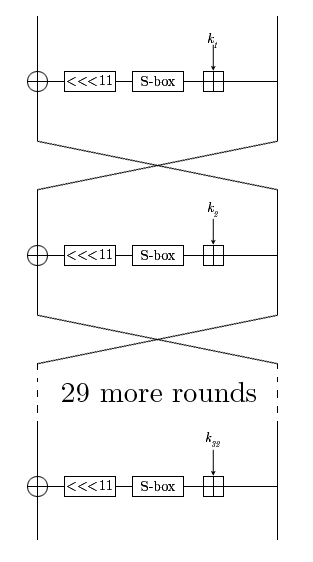
Анализировать полученные данные будем с помощью метода CPA.

Сначала необходимо выбрать промежуточное значение алгоритма, которое зависит от известных данных и небольшой части ключа и может быть рассчитано путем несложных преобразований. Обычно таким значением является выход S-box (в Магме теперь 1 таблица замен, поэтому проводить подобные атаки проще) первого (известны открытые тексты) или последнего раунда (известны шифротексты).

Я исследовал ключ с известными открытыми текстами, поэтому далее будет рассматриваться этот вариант. В алгоритме Магма, в отличие от DES, AES сложение 32-битного блока с раундовым ключом происходит по модулю 2³², следовательно, лучше начинать анализ с последних выходов S-box, так как сложение старших значений никак не влияет на младшие. Рассматриваем выход каждого S-box: сначала 8, потом учитывая 8, 7 и так до первого. Снятие трасс проводилось на 8-битном микроконтроллере, и можно предположить, что он работал со сдвоенными S-box-ами. Поэтому я атаковать буду сразу по 1 байту.

Вычисление модели энергопотребления для последнего байта ключа:

    for kguess in range(0,  256):
    #Initialize arrays & variables to zero
    sumnum = np.zeros(numpoint)
    sumden1 = np.zeros(numpoint)
    sumden2 = np.zeros(numpoint)
    hyp = np.zeros(numtraces)
    for tnum in range(numtraces):
        hyp[tnum] = HW[leak("Gost28147_tc26_ParamZ",  kguess, block2ns(text[tnum])[0], 0)]

где функция leak, просто возвращает выход S-box последнего байта.

Рассчитываем линейный коэффициент Пирсона для моделируемого и реального значения по формуле:

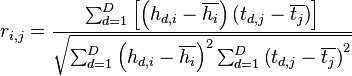
    cpaoutput = [0]*256
    maxcpa = [0]*256
        #Mean of hypothesis
        meanh = np.mean(hyp, dtype=np.float64)
        #Mean of all points in trace
        meant = np.mean(traces, axis=0, dtype=np.float64)
        #For each trace, do the following
        for tnum in range(0, numtraces):
            hdiff = (hyp[tnum] - meanh)
            tdiff = traces[tnum,:] - meant
            sumnum = sumnum + (hdiff*tdiff)
            sumden1 = sumden1 + hdiff*hdiff
            sumden2 = sumden2 + tdiff*tdiff
        cpaoutput[kguess] = sumnum / np.sqrt( sumden1 * sumden2 )
        maxcpa[kguess] = max(abs(cpaoutput[kguess]))

При выборе истинного подключа коэффициент корреляции будет иметь значительный всплеск:

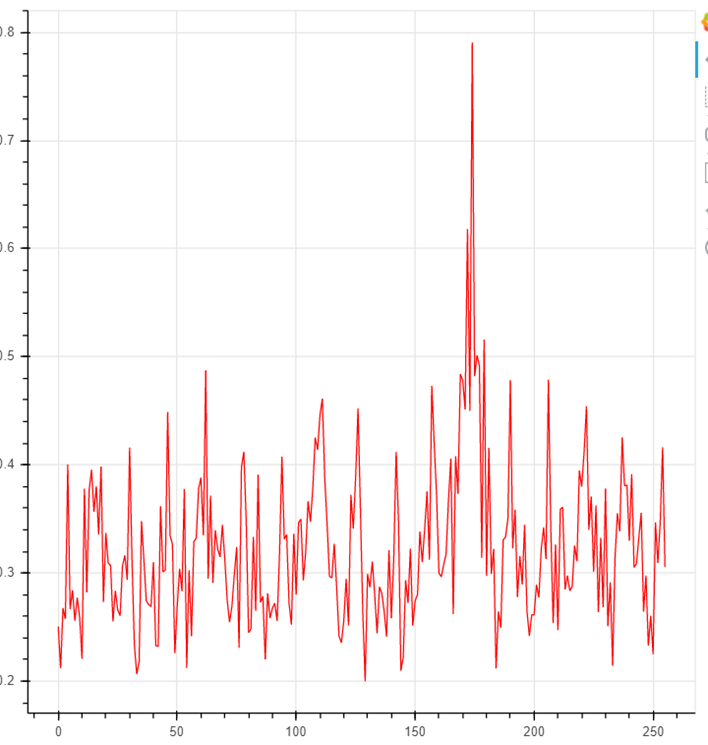
Таким образом анализируется каждый байт раундового ключа.

    for bnum in range(0, 4):
        cpaoutput = [0]*256
        maxcpa = [0]*256
        for kguess in range(0,  256):
            best_round_key = kguess << (bnum * 8) | best_round
            ...

Учитывая первый раундовый ключ, мы можем таким же образом высчитывать 2 и последующие раундовые ключи. Полный ключ Магмы можно получить, достав 8 раундовых ключей.

В процессе решения поставленной задачи возникает несколько нюансов. В отличие от шифров AES, DES, Кузнечик, сложение раундового ключа с открытым текстом происходит по модулю 2³². Сложение младших битов влияет на старшие, в отличие от XORa. При расчете каждого следующего подключа приходится учитывать результаты прошлого. Аналогично и с раундовыми ключами. Данные очень чувствительны. При неправильном расчете одного из значений дальнейший расчет всего ключа будет неправильным.

Также стоит учесть, что сейчас довольно сложно найти чип, имеющий четырехразрядную архитектуру: большая часть чипов имеет восьмиразрядную. Конечно, существуют специализированные криптографические чипы, которые проектируются под конкретный алгоритм защитного преобразования (или несколько алгоритмов) и имеют наиболее эффективную архитектуру.

Для выполнения шифра DES такой криптопроцессор может иметь шестиразрядную архитектуру, для «Магмы» — четырехразрядную, что позволяет обрабатывать каждый S-box отдельно. Мое целевое устройство 8-битное, и в случае «Магмы» за один подход будет производиться преобразование над восьмью битами, т.е. замена будет происходить на 2 S-box, энергопотребление будет считаться для 2 S-box. Если один из S-box, старший или младший, совпадает с истинным ключом, а другой не совпадает, могут возникать высокие корреляционные всплески.

Учитывая все вышесказанное, на выходе имеем следующий скрипт для анализа трасс энергопотребления для шифра Магма:

    import numpy as np
    path = r'C:Usersuserchipwhispererprojectsgost_10000_2_datatraces2019.08.11-19.53.25_'
    traces = np.load(path + 'traces.npy')
    text   = np.load(path + 'textin.npy')
    keys   = np.load(path + 'keylist.npy')
    HW = [bin(n).count("1") for n in range(0,256)]
    SBOXES = {"Gost28147_tc26_ParamZ": (
            (12, 4, 6, 2, 10, 5, 11, 9, 14, 8, 13, 7, 0, 3, 15, 1),
            (6, 8, 2, 3, 9, 10, 5, 12, 1, 14, 4, 7, 11, 13, 0, 15),
            (11, 3, 5, 8, 2, 15, 10, 13, 14, 1, 7, 4, 12, 9, 6, 0),
            (12, 8, 2, 1, 13, 4, 15, 6, 7, 0, 10, 5, 3, 14, 9, 11),
            (7, 15, 5, 10, 8, 1, 6, 13, 0, 9, 3, 14, 11, 4, 2, 12),
            (5, 13, 15, 6, 9, 2, 12, 10, 11, 7, 8, 1, 4, 3, 14, 0),
            (8, 14, 2, 5, 6, 9, 1, 12, 15, 4, 11, 0, 13, 10, 3, 7),
            (1, 7, 14, 13, 0, 5, 8, 3, 4, 15, 10, 6, 9, 12, 11, 2),
        )}

    def _K(s, _in):
        """ S-box substitution
        :param s: S-box
        :param _in: 32-bit word
        :returns: substituted 32-bit word
        """
        return (
            (s[0][(_in >> 0) & 0x0F] << 0) +
            (s[1][(_in >> 4) & 0x0F] << 4) +
            (s[2][(_in >> 8) & 0x0F] << 8) +
            (s[3][(_in >> 12) & 0x0F] << 12) +
            (s[4][(_in >> 16) & 0x0F] << 16) +
            (s[5][(_in >> 20) & 0x0F] << 20) +
            (s[6][(_in >> 24) & 0x0F] << 24) +
            (s[7][(_in >> 28) & 0x0F] << 28)
        )
    def block2ns(data):
        """ Convert block to N1 and N2 integers
        """
        data = bytearray(data)
        return (
            data[7] | data[6] << 8 | data[5] << 16 | data[4] << 24,
            data[3] | data[2] << 8 | data[1] << 16 | data[0] << 24,
        )
    def addmod(x, y, mod=2 ** 32):
        """ Modulo adding of two integers
        """
        r = x + int(y)
        return r if r < mod else r - mod
    def _shift11(x):
        """ 11-bit cyclic shift
        """
        return ((x << 11) & (2 ** 32 - 1)) | ((x >> (32 - 11)) & (2 ** 32 - 1))
    def round(sbox, key, data, byte):
        s = SBOXES[sbox]
        _in = addmod(data, key)
        sbox_leak = _K(s, _in);
        return (sbox_leak >> (8 * byte)) & 0xFF
    def Feistel(sbox, key, data, nround):
        s = SBOXES[sbox]
        w = bytearray(key)
        x = [
            w[3 + i * 4] |
            w[2 + i * 4] << 8 |
            w[1 + i * 4] << 16 |
            w[0 + i * 4] << 24 for i in range(8)
        ]
        n1, n2 = block2ns(data)
        for i in range(nround):
            n1, n2 = _shift11(_K(s, addmod(n1, x[i]))) ^ n2, n1
        return n1
    numtraces = len(traces)
    numpoint = np.shape(traces)[1]
    bestguess = [0]*32
    round_data = [0] * numtraces
    for i in range(numtraces):
        round_data[i] = [0] * 8
    for rnum in range(0, 8):
        best_round = 0
        for tnum_r in range(numtraces):
            round_data[tnum_r][rnum] = Feistel("Gost28147_tc26_ParamZ", bestguess, text[tnum_r], rnum)
        for bnum in range(0, 4):
            cpaoutput = [0]*256
            maxcpa = [0]*256
            for kguess in range(0,  256):
                #Initialize arrays & variables to zero
                best_round_key = kguess << (bnum * 8) | best_round
                sumnum = np.zeros(numpoint)
                sumden1 = np.zeros(numpoint)
                sumden2 = np.zeros(numpoint)
                hyp = np.zeros(numtraces)
                for tnum in range(numtraces):
                    hyp[tnum] = HW[round("Gost28147_tc26_ParamZ",  best_round_key, round_data[tnum][rnum], bnum)]
                #Mean of hypothesis
                meanh = np.mean(hyp, dtype=np.float64)
                #Mean of all points in trace
                meant = np.mean(traces, axis=0, dtype=np.float64)
                #For each trace, do the following
                for tnum in range(0, numtraces):
                    hdiff = (hyp[tnum] - meanh)
                    tdiff = traces[tnum,:] - meant
                    sumnum = sumnum + (hdiff*tdiff)
                    sumden1 = sumden1 + hdiff*hdiff
                    sumden2 = sumden2 + tdiff*tdiff
                cpaoutput[kguess] = sumnum / np.sqrt( sumden1 * sumden2 )
                maxcpa[kguess] = max(abs(cpaoutput[kguess]))
            best_round = best_round | (np.argmax(maxcpa) << (bnum * 8))
            bestguess[((rnum + 1) * 4)-bnum - 1] = np.argmax(maxcpa)
    print "Best Key Guess: "
    for b in bestguess: print "%02x "%b,

Репозиторий с результатами на GitHub

Выводы

В рамках исследования я работал с ChipWhisperer. Несмотря на то, что я попробовал не все инструменты (например, глитчинг), я однозначно нахожу ChipWhisperer полезным, особенно если не хочется покупать дорогое специальное железо.

Что касается анализа нашего шифра на энергопотребление, то он устойчивее к данной атаке, чем описанные выше шифры, но при достаточном количестве данных ключ можно достать без проблем.

Интересные материалы:

• P. Kocher Differential Power Analysis
• «Power Analysis Attacks: Revealing the Secrets of Smart Cards»
• Криптография под прицелом I: ищем ключи криптографических алгоритмов Р. Коркикян.
• Криптография под прицелом II: дифференциальный анализ питания Р. Коркикян.
• Доклад с ZeroNights 2014 Р. Коркикян.
• cryptocoding v2 с ZeroNights 2014 про программную реализацию.

Автор: forkyforky

Источник