Приветствую Хабр. Не так давно здесь уже появлялись статьи на эту тему Verilog. Цифровой фильтр на RAM и Построение цифрового фильтра с конечной импульсной характеристикой. Хочу и я внести свой скромный вклад и представить вашему вниманию реализацию цифрового БИХ-фильтра на Verilog.
Не смотря на то, что занимающиеся данной темой всё из ниже описанного знают, хочу, для начала, все-таки дать совсем немного теории для широкого круга читателей.
БИХ-фильтр(IIR-фильтр) — фильтр с бесконечной импульсной характеристикой (infinite impulse response). Отличительной чертой этого типа фильтра от КИХ-фильтра (фильтр с конечной импульсной характеристикой) является наличие обратной связи, когда значение на выходе фильтра зависит не только от входных данных, но и от выходных данных, полученных фильтром на предыдущих итерациях. Структуру БИХ-фильтра можно представить следующим образом:
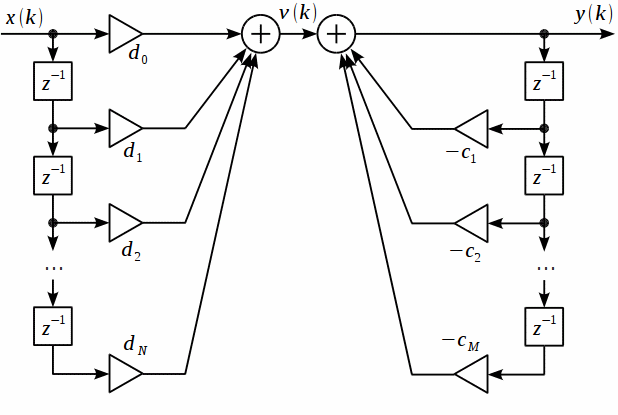
Не буду останавливаться на методиках расчета коэффициентов аналогового фильтра, с этой темой можно ознакомиться в большом количестве изданий, таких как Аналоговые и цифровые фильтры. Расчет и реализация Г.Лем или Синтез фильтров. Херреро Дж. Уиллонер Г. Так же существует много программ, позволяющих это сделать. Опишу кратко только процесс преобразования аналогового фильтра в цифровой.
Любой фильтр можно представить с помощью аналоговой передаточной функции. Например для БИХ-фильтра второго порядка она будет выглядеть так:
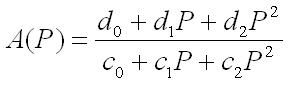
Подставив в это выражение вместо нормированной комплексной переменной
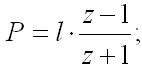
получим передаточную функцию A(z), которая может быть реализована в цифровом фильтре:
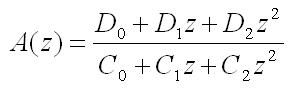
Коэффициенты для фильтра 2-го порядка будут определяться по следующим формулам:
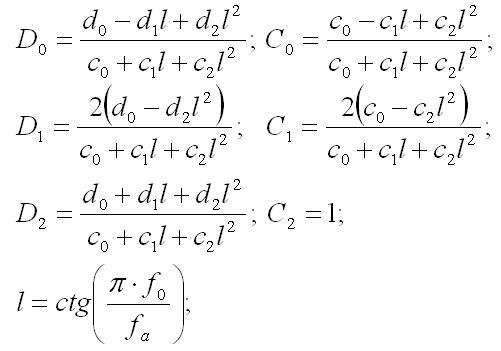
где
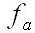— тактовая частота
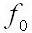— частота среза фильтра
d0...2 и с0...2 — коэффициенты аналогового фильтра, предполагается что вы их посчитали заранее.
Воспользовавшись этими нехитрыми вычислениями и зная соответствующие коэффициенты для аналогового фильтра, можно рассчитать коэффициенты для цифровой передаточной функции фильтра любого порядка. (Меня, правда, в свое время хватило только до 4-го порядка, причем сложности никакой в этом нет, просто приходится много писать длинные формулы, упрощая по формулам сокращенного умножения. Зато вспомнил далекие школьные годы). Передо мной, например, стояла задача реализовать фильтр с перестраиваемыми характеристики, поэтому все коэффициенты рассчитывались на ПК и передавались в FPGA в виде 32-х разрядных чисел, преобразованные перед этим в формат с плавающей запятой.
Итак, имея коэффициенты цифровой передаточной функции, подставим их в разностное уравнение БИХ-фильтра:
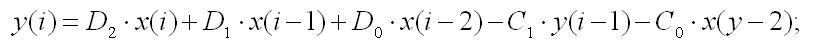
на основе которого уже не сложно написать реализацию на Verilog.
module LP_FILTER
(
mhz_clk,RESET,
D0,D1,D2,C0,C1,
X,Y,
COUNT
);
// low pass filter INPUT32 OUTPUT32
/*
y(i) = D2 * x(i) + D1 * x(i-1) + D0 * x(i-2) + C1 * y(i-1) + C0 * y(i-2)
A(z) = (D0+D1*z+D2*z*z)/(C0+C1*z+z*z) <==> A(P) = (d0+d1*P+d2*P*P)/(c0+c1*P+c2*P*P)
A(P) = 1/(1+1.4*P+P*P) LPF
D0 = ( d0 - d1*l + d2*l*l)/(c0 + c1*l + c2*l*l)
D1 = (2*d0 - 2*d2*l*l)/(c0 + c1*l + c2*l*l)
D2 = ( d0 + d1*l + d2*l*l)/(c0 + c1*l + c2*l*l)
C0 = -( c0 - c1*l + c2*l*l)/(c0 + c1*l + c2*l*l)
C1 = -(2*c0 - 2*c2*l*l)/(c0 + c1*l + c2*l*l)
l = ctg ( 3.14 * f_filt / f_samp )
*/
input mhz_clk;
input RESET;
input [17:0] X;
input [31:0] D0;
input [31:0] D1;
input [31:0] D2;
input [31:0] C0;
input [31:0] C1;
output [17:0] Y;
output [5:0] COUNT;
// adc-filter counter
reg [5:0] COUNT;
always @( posedge mhz_clk,negedge RESET )
if (~RESET) COUNT[5:0] = 0;
else if (COUNT[5:0] == 49) COUNT[5:0] = 0;
else COUNT[5:0] = COUNT[5:0] + 1;
// input - COUNT[4:0] = 24:49
// output - COUNT[4:0] = 6
reg [31:0] c0_y2;
reg [31:0] c1_y1;
reg [31:0] d0_x2;
reg [31:0] d1_x1;
reg [31:0] d2_x0;
reg [31:0] y0;
reg [31:0] y1;
reg [31:0] y2;
reg [31:0] x0;
reg [31:0] x1;
reg [31:0] x2;
// y(i) = D2 * x(i) + D1 * x(i-1) + D0 * x(i-2) + C1 * y(i-1) + C0 * y(i-2)
reg [31:0] mul_a;
reg [31:0] mul_b;
always @(*)
if ( ( COUNT[5:0] >= 0 ) & ( COUNT[5:0] <= 4 ) | ( COUNT[5:0] == 49 ) ) mul_a[31:0] = x0[31:0];
else if ( ( COUNT[5:0] >= 5 ) & ( COUNT[5:0] <= 10 ) ) mul_a[31:0] = x1[31:0];
else if ( ( COUNT[5:0] >= 11 ) & ( COUNT[5:0] <= 16 ) ) mul_a[31:0] = x2[31:0];
else if ( ( COUNT[5:0] >= 17 ) & ( COUNT[5:0] <= 22 ) ) mul_a[31:0] = y1[31:0];
else mul_a[31:0] = y2[31:0];
always @(*)
if ( ( COUNT[5:0] >= 0 ) & ( COUNT[5:0] <= 4 ) | ( COUNT[5:0] == 49 ) ) mul_b[31:0] = D2[31:0];
else if ( ( COUNT[5:0] >= 5 ) & ( COUNT[5:0] <= 10 ) ) mul_b[31:0] = D1[31:0];
else if ( ( COUNT[5:0] >= 11 ) & ( COUNT[5:0] <= 16 ) ) mul_b[31:0] = D0[31:0];
else if ( ( COUNT[5:0] >= 17 ) & ( COUNT[5:0] <= 22 ) ) mul_b[31:0] = C1[31:0];
else mul_b[31:0] = C0[31:0];
wire [31:0] mul_out;
mul_float32 ( 1, mhz_clk, mul_a[31:0], mul_b[31:0], mul_out[31:0] );
reg [31:0] outmul;
always @(*) outmul[31:0]=mul_out[31:0];
always @( posedge mhz_clk,negedge RESET )
if (~RESET) d2_x0[31:0] = 32'h0;
else if ( COUNT[5:0] == 4 ) d2_x0[31:0] = mul_out[31:0];
always @( posedge mhz_clk,negedge RESET )
if (~RESET) d1_x1[31:0] = 32'h0;
else if ( COUNT[5:0] == 10 ) d1_x1[31:0] = mul_out[31:0];
always @( posedge mhz_clk,negedge RESET )
if (~RESET) d0_x2[31:0] = 32'h0;
else if ( COUNT[5:0] == 16 ) d0_x2[31:0] = mul_out[31:0];
always @( posedge mhz_clk,negedge RESET )
if (~RESET) c1_y1[31:0] = 32'h0;
else if ( COUNT[5:0] == 22 ) c1_y1[31:0] = mul_out[31:0];
always @( posedge mhz_clk,negedge RESET )
if (~RESET) c0_y2[31:0] = 32'h0;
else if ( COUNT[5:0] == 28 ) c0_y2[31:0] = mul_out[31:0];
// y(i) = D2 * x(i) + D1 * x(i-1) + D0 * x(i-2) + C1 * y(i-1) + C0 * y(i-2)
reg [31:0] sum_a;
reg [31:0] sum_b;
always @(*)
if ( ( COUNT[5:0] >= 0 ) & ( COUNT[5:0] <= 18 ) | ( COUNT[5:0] == 49 ) ) sum_a[31:0] = d2_x0[31:0];
else if ( ( COUNT[5:0] >= 19 ) & ( COUNT[5:0] <= 26 ) ) sum_a[31:0] = d0_x2[31:0];
else if ( ( COUNT[5:0] >= 27 ) & ( COUNT[5:0] <= 34 ) ) sum_a[31:0] = c1_y1[31:0];
else sum_a[31:0] = c0_y2[31:0];
always @(*)
if ( ( COUNT[5:0] >= 0 ) & ( COUNT[5:0] <= 18 ) | ( COUNT[5:0] == 49 ) ) sum_b[31:0] = d1_x1[31:0];
else sum_b[31:0] = y0[31:0];
wire [31:0] sum_out;
sum_float32 ( 1, mhz_clk, sum_a[31:0], sum_b[31:0], sum_out[31:0] );
reg [31:0] outsum;
always @(*) outsum[31:0]=sum_out[31:0];
always @( posedge mhz_clk,negedge RESET )
if (~RESET) y0[31:0] = 32'h0;
else if ( ( COUNT[5:0] == 18 ) | ( COUNT[5:0] == 26 ) | ( COUNT[5:0] == 34 ) | ( COUNT[5:0] == 42 ) ) y0[31:0] = sum_out[31:0];
reg [17:0] int_to_float_in;
always @(*) begin int_to_float_in[17:0] = X[17:0];end
wire [31:0] int_to_float_out;
int18_to_float32 ( 1, mhz_clk, int_to_float_in[17:0], int_to_float_out[31:0] );
always @( posedge mhz_clk,negedge RESET )
if (~RESET) x0[31:0] = 32'h0;
else if ( COUNT[5:0] == 49 ) x0[31:0] = int_to_float_out[31:0];
always @( posedge mhz_clk,negedge RESET )
if (~RESET) x1[31:0] = 32'h0;
else if ( COUNT[5:0] == 49 ) x1[31:0] = x0[31:0];
always @( posedge mhz_clk,negedge RESET )
if (~RESET) x2[31:0] = 32'h0;
else if ( COUNT[5:0] == 49 ) x2[31:0] = x1[31:0];
always @( posedge mhz_clk,negedge RESET )
if (~RESET) y1[31:0] = 32'h0;
else if ( COUNT[5:0] == 49 ) y1[31:0] = sum_out[31:0];
always @( posedge mhz_clk,negedge RESET )
if (~RESET) y2[31:0] = 32'h0;
else if ( COUNT[5:0] == 49 ) y2[31:0] = y1[31:0];
wire [17:0] float_to_int_out;
wire nan;
wire overflow;
wire underflow;
float32_to_int18 ( 1, mhz_clk, y0[31:0], nan, overflow, float_to_int_out[17:0], underflow );
reg [17:0] Y;
always @( posedge mhz_clk ) if ( COUNT[4:0] == 6 ) Y[17:0] = float_to_int_out[17:0];
endmodule
Программа представляет собой законченный модуль, готовый к включению в существующий проект. Входные данные передаются в него в виде 18-ти разрядных целых чисел. (Возможно кому-то покажется странным такая разрядность, поясню сразу, что на разработанной плате используется 18-ти разрядная АЦП AD7643). Далее они преобразовываются в 32-х разрядный формат с плавающей точкой. Это выполняется по-средствам стандартной альтеровской мегафункции int18_to_float32. Сложение и умножение реализовано так же стандартными функциями sum_float32 и mul_float32 соответственно. После выполнения необходимых вычислений результат конвертируется в целое 18-ти разрядной число функцией float32_to_int18. С помощью предварительно рассчитанных коэффициентов можно превратить этот модуль как в фильтр нижних частот, верхних частот либо полосовой.
Архив проекта в Quartus II 9.1
Помимо уже упомянутых в тексте книг данных из Википедии при написании топика использовалось справочное руководство Полупроводниковая схемотехника. Титце У., Шенк К. и Структуры цифровых фильтров и их характеристики
Прошу прощения за некоторую сумбурность изложения, т.к. литературный талант никогда не являлся моей отличительной чертой, и спасибо за внимание.
Автор: nkie
