Привет!
В одной из прошлых статей мы познакомились с таким понятием как Feature Engineering и применением его на практике. В комментариях было озвучено пожелание показать на примере, как искусство генерации признаков помогает заметно улучшить качество алгоритмов машинного обучения. Я поискал задачи, в которых бы это можно было наглядно продемонстрировать и нашел один хороший пример. Это задача Forest Cover Type Prediction. Покажем, как можно применяя простые идеи, не содержащие в себе машинное обучение, сразу попасть в топ 10% Leader Board!
Не будем подробно описывать условие задачи, желающие могут ознакомиться с ним на странице соревнования. Отдалившись от предметной области, скажем лишь, что решается классическая задача многоклассовой классификации обьектов. Не будем в данном месте также приводить простые решения, которые сразу приходят в голову — запуск стандартных алгоритмов на всем множестве признаков или с предварительным отбором последних — все это дает сразу точность (Accuracy) не более 0.6-0.7
Давайте лучше забудем пока про сложные алгоритмы машинного обучения, а просто посмотрим на данные, которые есть в этой задаче. Для начала, взглянем на распределение нескольких признаков (остальные признаки — бинарные)
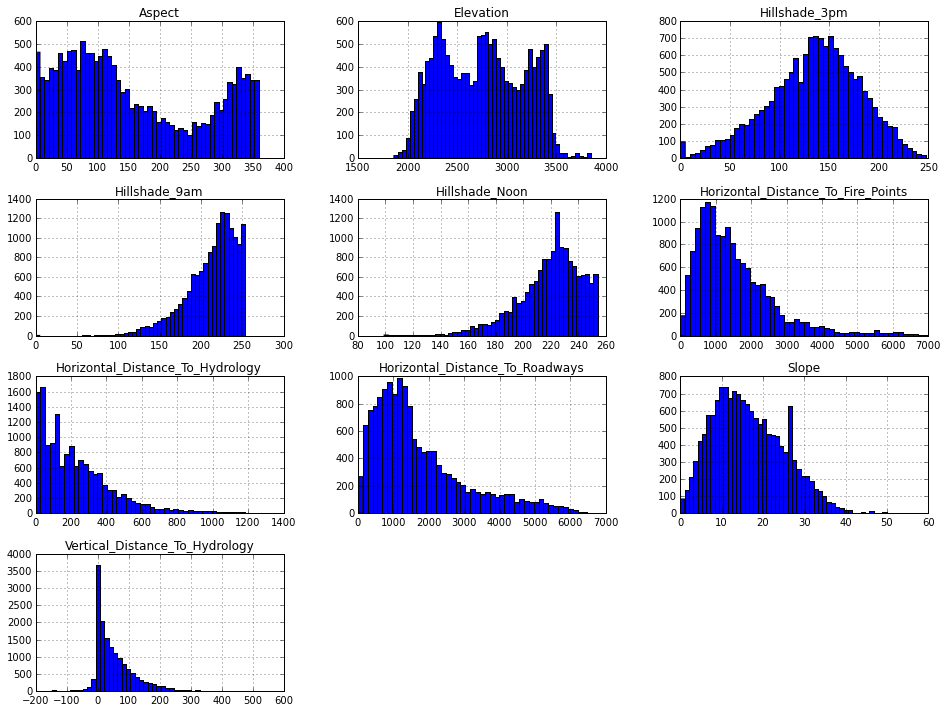
Как видим, признаки имеют довольно разные распределения (о физическом их смысле предлагается порассуждать читателю), однако, можно заметить один интересный момент — у признака Vertical_Distance_To_Hydrology один из хвостов выходит за значение 0. Таким образом, вспоминая обзор по Feature Engineering напрашивается ввести новый бинарный признак, который будет равен значению логического выражения [Vertical_Distance_To_Hydrology < 0]
Помимо этого часто на практике бывает так, что полезно просто включить некий здравый смысл и подумать, что же реально в конкретной задаче может влиять на целевую переменную (как это было отмечено в примере с ценами на жилье в одном из предыдущих постов), а именно:
Понятно, что если имеются такие признаки, как Horizontal_Distance_To_Hydrology и Vertical_Distance_To_Hydrology, то первое, что напрашивается — это просто посчитать расстояние — корень из суммы квадратов и записать это как новый признак Distanse_to_Hydrolody
Очевидно также, что если есть расстояния от одного обьекта до некоторых двух других, то (в данной задаче) можно в качестве признаков также рассматривать «относительные расстояния», а именно — добавить в качестве признаков попарную сумму/разницу следующих:
Horizontal_Distance_To_Hydrology
Horizontal_Distance_To_Roadways
Horizontal_Distance_To_Fire_Points
И того, получив еще +6 новых признаков. Читателю предлагается в данном месте немного подумать и предложить еще несколько вариантов того, как можно из имеющихся признаков сгенерировать новые.
А теперь самое интересное и наглядное, из-за чего я выбрал эту задачу. Такое бывает достаточно редко и найти это можно, только долго вглядываясь в данные. Но, заметив неочевидную закономерность, можно существенно увеличить качество алгоритма. Посмотрим внимательно на зависимость Elevation от Vertical_Distance_To_Hydrology:
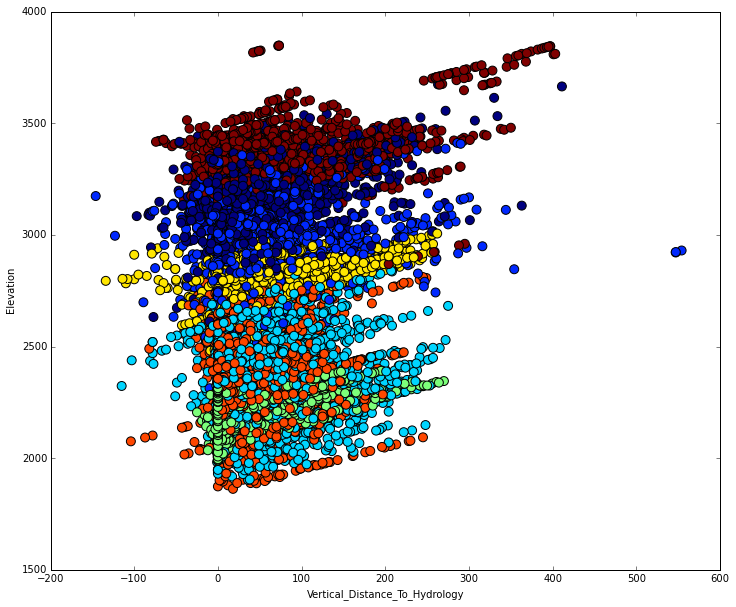
У читателя, наверное, возникло ощущение, что данные в некотором смысле упорядочены и достаточно хорошо разделяются. Это как раз есть одна из самых красивых закономерностей в данной задаче, заметить которую не так сложно. Теперь понятно, что необходимо в качестве одного из ключевых признаков рассмотреть разницу между Elevation и Vertical_Distance_To_Hydrology. Именно такие находки зачастую позволяют извлекать максимум из имеющихся данных. Фактически уже сейчас можно построить достаточно качественный классификатор. При этом мы не применяли еще никаких техник машинного обучения.
Постараюсь обьяснить, почему это хорошо работает. На самом деле, алгоритмы машинного обучения в целом (достаточн грубо) решают так или иначе задачу оптимизации. В случае задачи классификации это сводится к нахождению наилучшей разделяющей поверхности. Ровно это сейчас в пространстве признаков Elevation и Vertical_Distance_To_Hydrology мы с вами и сделали. Мы можем провести 6 разделяющих линий и получить первое приближение нашего классификатора
Чтобы не отнимать у читателя интерес к этой задаче, остановимся на поиске новых неочевидных закономерностей, которые в ней присутствуют. Используя только приведенные признаки, и строя них ансамбль из случайных деревьев, можно получить качество (Accuracy) близкое к 0.8. Этим примером я хотел показать, как зачастую на практике бывает полезно просто посмотреть на данные, прежде чем применять сложные алгоритмы, оптимизировать параметры и писать код!
Автор: akrot