Когда б Вы знали, из какого сора
растут стихи, не ведая стыда ...
Тема данного поста возникла совершенно неожиданно, в процессе чтения книги «Real-Time C++», более конкретно в процессе чтения раздела 6.13, в котором рассматривалось построение делителя измеряемого напряжения таким образом, чтобы получившийся результат легко (с применением только операции сдвига) масштабировался. Так вот, в конце раздела на странице 121 приводилась формула для оценки погрешности получаемой величины, которая привела меня в некоторое замешательство. Поскольку данную книгу «могут увидеть дети» и получить непоправимую травму психики, если некритично отнесутся к написанному, мною и создан настоящий пост с целью привнести определенный порядок в понимание методики оценки погрешностей измерений молодыми инженерами.
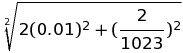
Для начала вспомним основные положения, определимся с терминологией и установим некоторые важные факты.
Любое измеренное значение всегда представляет собой лишь некоторое приближение к измеряемому параметру, и для оценки степени отклонения измеренной величины от точного значения вводят понятие погрешности dX = | X-Xo |, где dX — абсолютная погрешность, X — измеренное значение, Xo — истинное значение( предполагается, что мы его откуда-то знаем).
Также весьма важна относительная погрешность qX = dX / Xo (в тех же обозначениях), которая характеризует степень точности полученного результата значительно лучше абсолютной (хотя с ней есть определенные проблемы для Xо = 0). Тем не менее, относительная погрешность весьма часто применяется для указания параметров компонентов электронных схем в виде точности, например, резисторов — 5% либо 1%.
При этом следует иметь в виду, что нам указывается только максимальное значение отклонения номинала компонента от его ожидаемого значения, никаких предположений о законе распределения данного отклонения нет, это может быть и линейное распределение, и треугольное, и Гауссово с обрезанными хвостами, поэтому никаких предположений о среднеквадратичном отклонении мы не делаем и в дальнейшем оперируем только максимальным отклонением. Такой подход для нашего случая (мы ведь инженеры, а не дрессировщики) правильнее, вряд ли Ваших заказчиков устроит схема, которая будет работать в 98% случаев, спроектированная нами схема будет работать всегда (в пределах допустимых условий эксплуатации, конечно).
Поскольку измеренные параметры либо значения параметра компонента крайне редко используются в чистом виде, а чаще всего входят в состав разнообразных передаточных функций совместно с другими параметрами либо константами, нам необходимы правила вычисления точностных характеристик различных выражения подобного рода. Еще раз подчеркну, что мы оцениваем только максимальную ошибку.
Начнем с простейшей функции f(X) = K * X ( функция масштабирования) и получим точность для результата этой функции в зависимости от точности входящих в нее членов. Считая константу K заданной абсолютно точно, применим простейший способ прямого вычисления qf(X) = | f(X) — f(Xo) | / f(Xo), что приводит к выражению q(k*X) = | K * (Xo + dX) — K * Xo | / ( K * Xo), или q(K*X) = | K * dX | / ( K * Xo ) = dX / Xo, отсюда q(K*X) = qX, что означает, что при масштабирования относительная погрешность не меняется.
Следующая важная функция — взятие обратного значения f(X) = 1 / X, для нее получаем
q(1/X) = | 1 / ( Xo + dX) — 1 / Xo | / ( 1 / Xo ), после преобразований имеем
q(1/X) = | -dX / ( (Xo + dX) * Xo ) | * Xo = | -dX / ( Xo + dx ) |,
считая, что dX << Xo, получим q(1/X) ~ dX / Xo = qX, то есть при взятии обратного значения относительная погрешность остается неизменной.
Рассмотрим теперь функцию суммы f(X,Y) = X + Y. Проведем аналогичные вычисления и получим
q(X+Y) = | ( (Xo + dX ) + ( Yo + dY ) ) — ( Xo + Yo ) | / ( Xo + Yo ) = | dX + dY | / ( Xo + Yo ) = qX * Xo / (Xo + Yo) + qY * Yo / (Xo + Yo). Мы убедились, что при сложении двух величин абсолютные погрешности складываются, а относительные масштабируются в соответствии со значениями точных величин.
Если при этом относительные погрешности обоих величин совпадают, то мы получим q(X+Y) = qX * ( Xo + Yo ) / ( Xo + Yo ) = qX = qY, то есть при сложении двух величин с одинаковой относительной погрешностью относительная погрешность суммы будет такой же.
Из полученных результатов следует интересный вывод — относительная точность эквивалентного сопротивления любой резисторной схемы равна относительной точности входящих в нее компонентов и не зависит от номиналов и схемы соединения. Действительно, при последовательном соединении сопротивления складываются, а мы установили сохранение точности при сложении, а при параллельном соединении складываются проводимости (величины, обратные сопротивлению), а мы также установили сохранение точности при взятии обратного. Результат (по крайней мере, для меня) несколько неожиданный, но так получается.
Для дальнейшего рассмотрения нам потребуется также точность функции умножения двух величин, получим ее аналогично
q(X*Y) = | ( Xo + dX ) * ( Yo + dY ) — Xo * Yo | / ( Xo * Yo ) = | dX * Yo + dY * Xo + dX * dY | / ( Xo * Yo ) =
= dX / Xo + dY / Yo + dX / Xo * dY / Yo = qX + qY + qX*qY, учитывая qY ~ qY << 1, получим окончательно q(X*Y) = qX + qY, то есть при умножении относительные погрешности складываются.
Рассматривая деление, как умножение на обратное значение, данный результат распространяем и на деление q(X/Y) = qX + qY.
Теперь мы готовы рассчитать точность коэффициента передачи резистивного делителя, который определяется формулой
K(R,r) = r / ( R + r ). Для начала рассмотрим нашу формулу по частям и оценим qK(R,r) = qr + q(R+r) = qr +qR * R / ( R + r ) + qr * r / ( R +r ), считая qr = qR, получим qK(R,r) = 2 * qR.
Именно такой результат и использовался в указанной в самом начале поста книге, однако он не вполне верен, поскольку мы считали, что числитель и знаменатель дроби в нашей функции независимы, а это не так, и там и там используется общий параметр.
Уточним полученный результат, прибегнув к испытанному способу получения относительной погрешности и получим (промежуточные выкладки оставляем пытливому читателю и так меня наверняка будут ругать за неудобные написание формул, у меня Latex сегодня почему-то не работает, а тут будут многоэтажные выражения) qK(R,r) = ( qR + qr ) * R / ( R + r ).
Итак, мы видим, что уточненная формула погрешности показывает нам, что точность коэффициента передачи делителя зависит от коэффициента деления K = r / ( R + r ) в виде qK(R,r) = 2* qR * ( 1 — K ), то есть удвоение погрешности наступит только для очень маленьких коэффициентов передачи (K<<1), а, например, при коэффициенте делений 1/2 относительная погрешность коэффициента совпадет с относительной погрешностью резисторов, что опять-таки несколько неожиданно. Пр заданных в книге номиналах погрешность составит 2*64.9/(11.8+64.9)=1.7*qR, что, хоть и близко к первому результату (2*qR), но все-таки от него отстоит.
Ну и последнее замечание — поскольку я неоднократно подчеркивал, что мы оцениваем максимальное отклонение, вычисление среднеквадратичного значения никоим образом не может приветствоваться и, учитывая, что код на выходе АЦП описывается формулой N = Uвх * Kацп следует просто сложить относительные погрешности данных величин, получая qN = qUвх +qKацп = 1.7*0.01 + 2/1024 ~ 1.9% < 2%, что, впрочем, соответствует результату, указанному в книге.
Следует учесть еще одно немаловажное обстоятельство — если погрешность коэфиициента передач не зависит от входного напряжения, то про погрешность АЦП мы этого сказать не может — она составляет 2 ЕМР не зависимо от входного напряжения (на самом деле все намного сложнее, но мы так приняли для простоты), так что полученная относительная погрешность измерений верна только для напряжений, близких к максимальным, и в других случаях будет увеличиваться.
Автор: GarryC



