Для начала позвольте мне пожаловаться, что «greeble» — ужасное слово, которое нужно изгнать из словаря.
Ну, сняв камень с души, перейдём к объяснениям. Greeble — это мелкие повторяющиеся детали, добавляемые к модели, чтобы придать ей ощущение масштаба и определённой эстетики. Гриблы стали популярны благодаря классическим научно-фантастическим фильмам, в которых «моделью» часто была физическая скульптура:

Если вы уже знаете из моего туториала по экструдированию, как экструдировать процедурные меши, то понимаете, как добавить гриблы. Добавление простых гриблов к мешу можно реализовать экструдированием всех полигонов меша на случайную длину.
Однако вы могли заметить, что представленный выше туториал рассматривает только экструдирование треугольников, в то время как на изображении в начале статьи гриблы квадратные. Мне пришлось настроить меш так, чтобы он был разделён на четырёхугольники, и многие меши часто состоят из полигонов с более чем тремя индексами. Поэтому в этом туториале мы узнаем, как экструдировать полигон с n индексами и применим этот алгоритм ко всему мешу, чтобы создать гриблы. Также мы узнаем пару способов внесения вариаций в алгоритм гриблинга для получения менее однородных результатов.
Нормаль поверхности
Для начала давайте узнаем, как вычисляется нормаль полигона с произвольными n индексами. Если мы можем предположить, что этот полигон планарный, то есть все его вершины находятся на одной плоскости, то процесс не отличается от вычисления нормали полигона с тремя индексами.
Нормаль поверхности — это перпендикуляр к грани полигона, который можно вычислить, взяв векторное произведение двух векторов, указывающих вдоль ребра полигона.
Тогда мы нормализуем этот вектор, чтобы его длина была равна 1, так как от нормали поверхности нам нужно только направление, а не длина.
function getFaceNormal (mesh, poly) Vec3 v1 = mesh:getVertex(poly[1]) Vec3 v2 = mesh:getVertex(poly[2]) Vec3 v3 = mesh:getVertex(poly[3]) Vec3 e1 = v2 - v1 Vec3 e2 = v3 - v2 Vec3 normal = e1:cross(e2) return normal:normalize() end
Если мы не можем с уверенностью допустить, что полигон планарен, то представленный выше алгоритм отдаёт предпочтение плоскости, на которой находятся первые два индекса. Для более точного представления направления, в котором указывает полигон, мы можем вместо этого взять среднее всех векторных произведений рёбер:
function getFaceNormal (mesh, poly)
Vec3 n = Vec3(0, 0, 0)
for i = 1, #poly -2 do
Vec3 v1 = mesh:getVertex(poly[1])
Vec3 v2 = mesh:getVertex(poly[1+ i])
Vec3 v3 = mesh:getVertex(poly[2+ i])
n:add((v2 - v1):cross(v3 - v1))
end
return n:normalize()
end
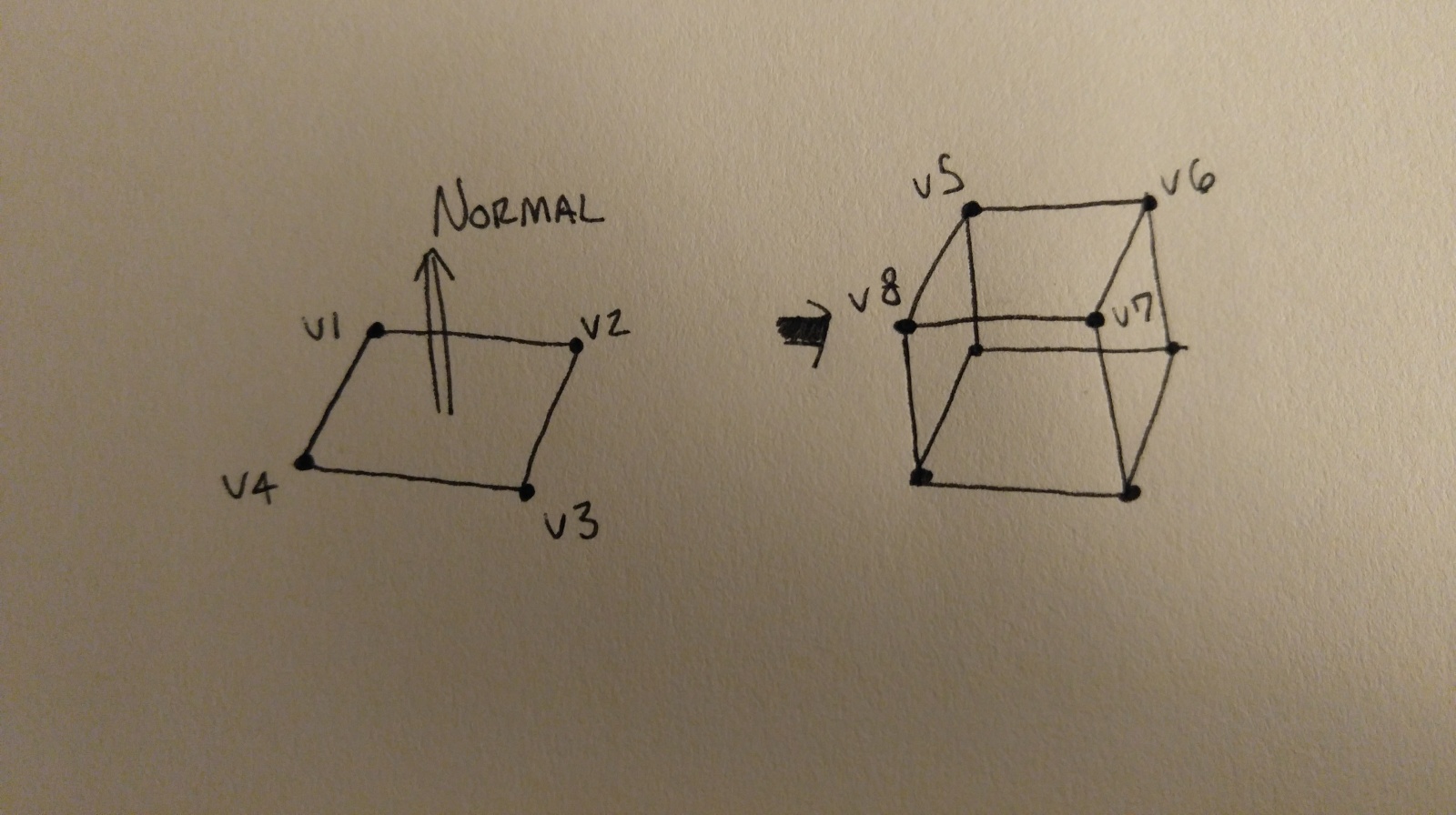
Пример, показывающий экструдирование планарного четырёхугольника.
Экструдирование
Теперь, когда у нас есть информация о нормали поверхности, мы готовы экструдировать полигон в направлении нормали. Если говорить просто, то для экструдирования полигона мы создаём новые вершины, перенося старые вершины в направлении нормали поверхности.
Более подробно:
- Создаём новые вершины «над» старыми в направлении нормали.
Новые вершины можно вычислить следующим образом:
(позиция старой вершины) + (направление нормали)
Это «сдвигает» старую позицию в направлении нормали поверхности.
Например, посмотрите на изображение выше, на нём v1 перемещается в направлении нормали к v5.
- Создаём четырёхугольники, чтобы связать новые и старые вершины.
Следует учесть, что для каждого индекса в новом полигоне создаётся один новый четырёхугольник.
Например, взгляните на четырёхугольник, созданный из v8, v7, v3 и v4.
- Заменяем старый полигон новым полигоном, созданным новыми вершинами. Например, взгляните на четырёхугольник, созданный из v5, v6, v7 и v8.
function extrudePoly (mesh, polyIndex, length)
int[] poly = mesh.polys[polyIndex]
int[] newPoly = []
Vec3 n = getFaceNormal(mesh, poly)
-- (1) Create extruded verts
for j = 1, #poly do
local p = mesh:getVertex(poly[j])
newPoly[#newPoly + 1] = #mesh.verts
-- length determines the length of the extrusion
mesh:addVertex(p + (n*length))
end
-- (2) Stitch extrusion sides with quads
for j0 = 1, #poly do
local j1 = j0 % #poly + 1
mesh:addQuad(
poly[j0],
poly[j1],
newPoly[j1],
newPoly[j0]
)
end
-- (3) Move existing face to extruded verticies
for j = 1, #poly do
mesh.polys[pi][j] = newPoly[j]
end
end

Равномерный гриблинг.
Гриблинг всего меша
Теперь, когда у нас есть функция getSurfaceNormal() и функция extrude(), выполнить гриблинг очень просто! Мы просто применяем функцию extrude() к каждому полигону меша. Используем экструдирование со случайной длиной, чтобы каждый экструдированный полигон имел немного отличающийся размер, что создаёт ощущение текстуры. Показанный ниже алгоритм применён к представленному выше кубу, который полностью состоит из четырёхугольников.
function greeble (mesh)
for i = 1, #mesh.polys do
-- these random values are arbitrary :p
float length = random:getUniformRange(0.1, 1.0)
extrudePoly(mesh, i, length)
end
return mesh
end
Поздравляю, наш гриблинг заработал. Но мы можем сделать больше! Сейчас гриблинг довольно однородный. Вот два примера модификаций, позволяющих сделать его более интересным.

Модификация 1: наличие гриблинга зависит от случайности
Это довольно просто: всего лишь бросаем кубик, чтобы определить, нужно ли применять гриблинг к каждому полигону. Благодаря этому гриблинг становится менее однородным. Показанный ниже алгоритм применён к представленному выше кубу.
for i = 1, #mesh.polys do
<strong>if random:chance(0.33) then</strong>
float length = random(0.1, 1.0)
extrudePoly(mesh, i, length)
end
end
return mesh
end

Модификация 2: добавляем экструдированию масштаб
Для этого требуется изменить алгоритм экструдирования. Когда мы создаём вершины экструдированного полигона, мы можем свести их по направлению к центру полигона на случайную величину, чтобы объект выглядел интереснее.
Для начала наша функция extrude() должна получать дополнительный параметр, определяющий величину сужения нового полигона. Мы определим его как Vec3 под названием scale. Чтобы переместить вершину по направлению к центру, мы интерполируем позицию вершины между её исходной позицией и центром полигона на величину scale.
(Если вам нужно узнать алгоритм нахождения центра полигона, то рекомендую быстро перескочить к туториалу о триангуляции и прочитать о триангуляции средней точки (centroid triangulation).)
-- find the center of the poly
Vec3 c = mesh:getFaceCentroid(poly)
for j = 1, #poly do
local p = mesh:getVertex(poly[j])
newPoly[#newPoly + 1] = #mesh.verts
self:addVertex (
math.lerp(c.x, p.x, scale.x) + n.x * length,
math.lerp(c.y, p.y, scale.y) + n.y * length,
math.lerp(c.z, p.z, scale.z) + n.z * length
)
mesh:addVertex(p + (n*length))
end
Теперь можно использовать его в алгоритме гриблинга, отмасшабировав на случайную величину для каждого полигона. Так мы получим показанное выше изображение.
function greeble (mesh)
for i = 1, #mesh.polys do
float length = random:getUniformRange(0.1, 1.0)
Vec3 scale = (random:getUniformRange(0.1, 1.0),
random:getUniformRange(0.1, 1.0),
random:getUniformRange(0.1, 1.0))
extrudePoly(mesh, i, length, scale)
end
return mesh
end
Конец
Отлично, мы добрались до завершения! Надеюсь, этот туториал был для вас полезным.
Автор: PatientZero