
В последнее время я играл в несколько roguelike, поэтому решил попробовать написать собственный процедурный генератор подземелий. Существует множество способов решения этой задачи, и я выбрал алгоритм автора TinyKeep, описанный здесь. Я расширил этот алгоритм, чтобы он работал в 3D и мог создавать многоэтажные подземелья.
Код примера выложен в репозитории Github. Для демонстрации я использую Unity3D, но эти концепции, разумеется, применимы к любому другому движку.
Два измерения
Сначала мне нужно написать алгоритм для двух измерений. В целом он работает так же, как алгоритм TinyKeep, но имеет отличия для создания более интересных уровней.
Сцена для этого примера называется Dungeon2D. Код для него находится в папке Scripts2D.
Алгоритм
Мир разделён в виде прямоугольной сетки. Я предполагаю, что 1 единицы будет достаточно для обозначения коридора. В полной игре 1 единица измерения Unity может соответствовать например 5 метрам. Для сетки я выбрал размер 30×30.
1. Располагаем комнаты произвольным образом, но так, чтобы они не накладывались друг на друга. Расположение не имеет значения, поэтому в этом примере я просто задаю им случайное расположение и размер. Также с каждой стороны я добавил буфер шириной 1 единицу (чтобы комнаты не касались друг друга), но это не обязательно для работы алгоритма.

Красные прямоугольники — это комнаты
2. Создаём граф триангуляции Делоне для комнат. Я использовал для этого алгоритм Боуэра-Ватсона. Существует множество реализаций этого алгоритма на многих языках, я выбрал тот, который легко будет перенести на C#.
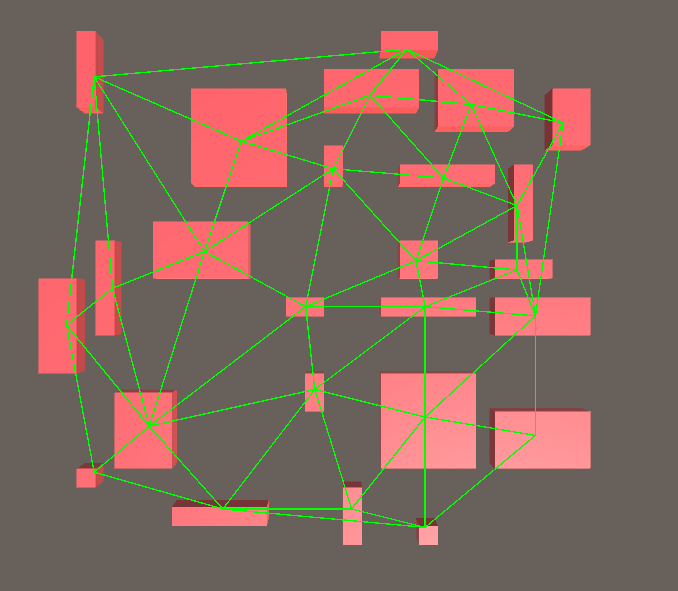
Триангуляция Делоне
3. Создаём из триангуляции минимальное остовное дерево (minimum spanning tree, MST). Я использовал для этого алгоритм Прима.

MST коридоров
4. Создаём список коридоров, начиная с каждого ребра дерева из этапа 3. Дерево содержит все комнаты, поэтому путь к каждой комнате гарантированно будет существовать. Случайным образом добавляем рёбра из триангуляции в список. Так мы создадим в коридорах несколько петель. В своём коде я использовал вероятность добавления каждого ребра 12,5%.
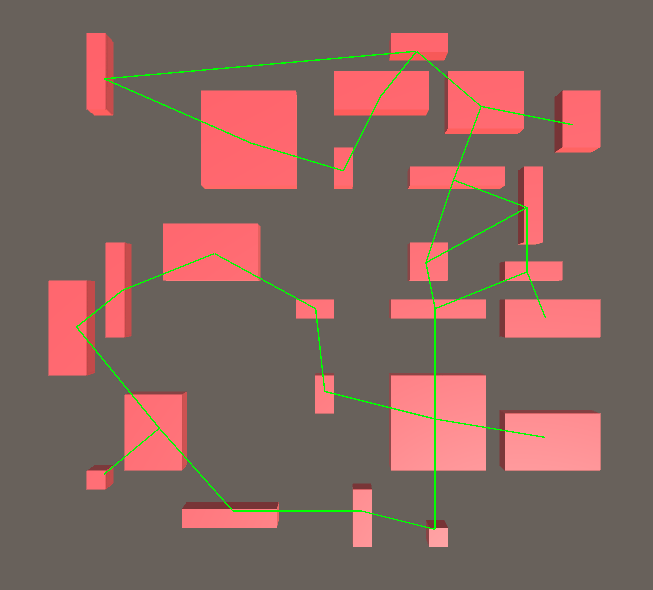
Коридоры после добавления нескольких рёбер в MST. Заметьте, что появились петли.
5. Для каждого коридора в списке используем алгоритм A*, чтобы найти пути от начала коридора до конца. После нахождения одного пути он изменяет состояние мира так, чтобы будущие коридоры всегда могли обходить мимо существующих.
Использованная мной функция затрат делает менее затратным движение по коридору, вырезанному в другой итерации, чем создание нового коридора. Это стимулирует алгоритм поиска пути комбинировать коридоры, проходящие через одно пространство. Движение через комнату возможно, но затратно. Поэтому в большинстве случаев алгоритм поиска пути предпочитает избегать комнат.

Синие прямоугольники — это коридоры
Вот несколько примеров алгоритма, использующего настоящие графические ресурсы (ресурсы и код для их размещения отсутствуют в репозитории):


Три измерения
Создав работающий генератор 2D-подземелий, я начал его перенос в 3D. Все использованные алгоритмы имеют 3D-версии, поэтому это должно быть просто, правда?
Алгоритм
Сетка теперь имеет размер 30x5x30.
1. Первым изменением стала генерация комнат в 3D. Это изменение тривиально.

Нужно учесть, что комнаты могут быть высотой в несколько этажей.
2. Затем находим 3D-триангуляцию Делоне этих комнат, или скорее тетраэдраляцию Делоне. Поискав информацию по запросам «3D Delaunay triangulation» или «Delaunay tetrahedralization», я нашёл множество исследовательских статей, но ни одного примера кода.
Самым близким к нужному мне была реализация 3D-триангуляции CGAL, но с ней возникли две проблемы. Первая — этот модуль был доступен только под лицензией GPL. Вторая — код был насколько шаблонизирован и малопонятен, что я так и не разобрался, где же реализуется алгоритм.
В конечном итое мне пришлось самому изучить принцип работы алгоритма Боуэра-Ватсона, чтобы изменить его самостоятельно. По-прежнему не очень понимаю, почему так важны описанные окружности, но мне по крайней мере удалось переписать алгоритм с описанными сферами, воспользовавшись этой страницей с Wolfram MathWorld. Так как в основном это операции с матрицами 4×4, всю сложную работу я поручил типу Matrix4x4 из Unity3D.
Эта новая версия находится в Scripts3D/Delaunay3D.cs, на случай, если кому нибудь понадобится легко понимаемый код с лицензией MIT.

Это сложно заметить, но вместо треугольника с тремя вершинами алгоритм теперь создаёт тетраэдр с 4 вершинами. По крайней мере одна из этих вершин будет находиться на другом этаже, ведь в противном случае тетраэдр окажется вырожденным. Это даёт этапу поиска пути множество возможностей двигаться между этажами.
3 и 4. Рёбра из этапа 2 с совершенно тривиальными изменениями можно передать алгоритму Прима.

3D-MST коридоров

Снова добавлены коридоры с несколькими рёбрами
5. Сложности начинаются при реализации в 3D алгоритма A*. 2D-версия ужасно проста, это стандартная реализация A*. Чтобы перенести её в 3D, мне нужно добавить алгоритму поиска пути возможность двигаться вверх и вниз и соединять комнаты на разных этажах. Я решил соединять этажи не вертикальными лестницами, а лестничными маршами.
В этом-то и заключается проблема. Лестничный марш сложнее, чем просто подъём вверх по вертикали. Чтобы двигаться по вертикали, лестнице нужно двигаться и по горизонтали. То есть у неё есть подъём и пролёт. Посмотрите на изображение ниже. Текущая ячейка — это сплошной синий квадрат. Возможные соседи — это пустые квадраты. Алгоритм поиска пути не может переместиться в ячейку непосредственно над текущей ячейкой. Вместо этого ему придётся двигаться одновременно по горизонтали и вертикали.

Вид сбоку. Узлы по бокам создать можно, но не узел сверху.
Чтобы создавать алгоритм поиска пути для лестницы, мне нужно было выбрать её форму. Соотношение высоты к длине 1:1 было бы слишком крутым, поэтому я выбрал соотношение 1:2. На каждую вертикальную единицу измерения лестница двигается на две горизонтальных единицы. Кроме того, чтобы персонаж помещался, над самой лестницей должно быть пространство, то есть две ячейки над лестницей тоже должны быть открыты. В целом, одна лестница занимает четыре ячейки:
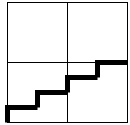
Лестница и свободное пространство над ней
Также наверху и внизу у лестниц должен быть коридор. Алгоритм поиска пути не должен иметь возможность приходить к лестнице сбоку или с противоположного направления. Будет непрактично и странно, ели лестница будет врезаться в коридор, как показано ниже.


То есть в конечном итоге формат лестницы должна выглядеть как на изображении ниже. Алгоритм поиска пути должен гарантировать существование коридоров в двух синих квадратах.
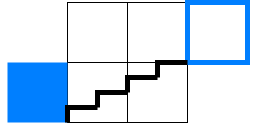
Лестница начинается со сплошного синего квадрата и движется вверх на один этаж
Алгоритм поиска пути должен двигаться из начальной в конечную точку за один шаг. Это значит, что он должен сдвигаться на 3 единицы по горизонтали и на 1 единицу вверх или вниз. Алгоритм A* рассчитан на перемещение в каждом шаге из одного узла в соседний. Чтобы создать лестницы, мне придётся «перепрыгивать» четыре ячейки лестницы.
Сложность заключается в том, что мне каким-то образом нужно заставить алгоритм обходить лестницы, которые он создаёт. Я не могу добавлять их в замкнутое множество A*, потому что тогда через эти ячейки не сможет пройти другой путь с другого направления. Но не могу я и оставить их, потому что тогда алгоритм поиска пути сможет двигаться по только что созданной лестнице, создавая показанные выше нежелательные ситуации.
Решение заключалось в том, что каждый узел должен отслеживать все предыдущие узлы на его пути. Тогда при рассмотрении соседнего узла он будет отклонён, если он относиться к пути текущего узла. Коридор в конце лестницы будет содержать все ячейки, занятые лестницей, узел в начале лестницы и все узлы на пути до него, и так до самого начала. Алгоритм поиска пути может создать другой путь, проходящий через лестницу, потому что второй путь не будет знать о лестнице.
Описанное выше поведение нужно только для нескольких потенциальных путей в пределах одного вызова функции поиска пути. Для генерации всех коридоров всё равно остаётся множество вызовов поиска пути. Последующие итерации просто как и раньше будут обходить существующие лестницы.
Алгоритм на этом этапе уже не совсем является A*. В нём слишком много особых случаев только для учёта лестниц. Необходимость проверки всего предыдущего пути на каждом этапе — затратный процесс. Наивная реализация следовала по всем узлам до начала, считывая их как связанный список. Тогда для проверки пути для каждого соседнего узла потребовалось бы время O(N).
Я выбрал такую реализацию: хранение в каждом узле хеш-таблицы, ключами которой являются предыдущие узлы. Благодаря этому проверка пути выполняется за O(1), однако при добавлении узла к пути хеш-таблицу нужно копировать, а это O(N). Я выбрал этот способ, потому что понял, что алгоритм будет считывать пути чаще, чем их изменять.
Как бы то ни было, общая сложность будет примерно O(N^2), хотя я не знаю, как это правильно проанализировать. Эта модификация — основное «бутылочное горлышко» алгоритма генерации подземелий.
После внесения всех этих изменений результат оказался таким:

Зелёные прямоугольники — это лестницы

Создаваемые генератором пути могут быть простыми...

… или сложными
Вот как выглядит 3D-подземелье с настоящими графическими ресурсами:

Подземелье с несколькими этажами
Алгоритм генерации подземелий способен создавать интересные эмергентные поведения.

Две лестницы образуют лестницу двойной ширины

Труднообъяснимая лестница тройной ширины

Путь, спускающийся на два этажа, может создать две лестницы с площадкой посередине

Когда несколько путей проходят рядом друг с другом, коридоры могут оказаться довольно большими

Две лестницы спускаются на один этаж
Вывод
Самой сложной частью проекта было создание алгоритмов, необходимых для 3D-версии. Я не смог найти ни одной реализации 3D-триангуляции Делоне, поэтому пришлось делать её самостоятельно. Требования к алгоритму поиска пути были очень специфичными, поэтому её я тоже делал сам.
Но работа того стоила. Созданные этим алгоритмом подземелья интересны и могут стать фундаментом для хорошей игры.
Автор: PatientZero



