
В этой статье мы подробнее рассмотрим то, что происходит с 3D-миром после завершения обработки всех его вершин. Нам снова придётся стряхнуть пыль с учебников по математике, освоиться в геометрии пирамид усечения и решить загадку перспектив. Также мы ненадолго погрузимся в физику трассировки лучей, освещения и материалов.
Главная тема этой статьи — важный этап рендеринга, на котором трёхмерный мир точек, отрезков и треугольников становится двухмерной сеткой разноцветных блоков. Очень часто этот процесс кажется незаметным, потому что преобразование из 3D в 2D оказывается невидимым, в отличие от процесса, описанного в предыдущей статье, где мы сразу же могли увидеть влияние вершинных шейдеров и тесселяции. Если вы пока не готовы к этому, то можете начать с нашей статьи 3D Game Rendering 101.
Подготовка к двум измерениям
Подавляющее большинство читателей читают этот веб-сайт на совершенно плоском мониторе или экране смартфона; но даже если у вас есть современная техника — изогнутый монитор, то отображаемая им картинка тоже состоит из плоской сетки разноцветных пикселей. Тем не менее, когда вы играете в новую Call of Mario: Deathduty Battleyard, изображения кажутся трёхмерными. Объекты движутся по сцене, становятся больше или меньше, приближаясь и отдаляясь от камеры.

Взяв в качестве примера Fallout 4 компании Bethesda, вышедшую в 2014 году, мы можем легко увидеть, как обрабатываются вершины, создавая ощущение глубины и расстояния; особенно хорошо это заметно в каркасном режиме (см. выше).
Если взять любую 3D-игру за последние два десятка лет, то почти каждая из них для преобразования 3D-мира вершин в 2D-массив пикселей выполняет одинаковую последовательность действий. Такое преобразование часто называют растеризацией, но это только один из множества этапов во всём процессе.
Нам нужно разобрать разные этапы и исследовать применяемые в них техники и вычисления. В качестве справочного материала мы воспользуемся последовательностью, применяемой в Direct3D. На изображении ниже показано, что происходит с каждой вершиной мира:
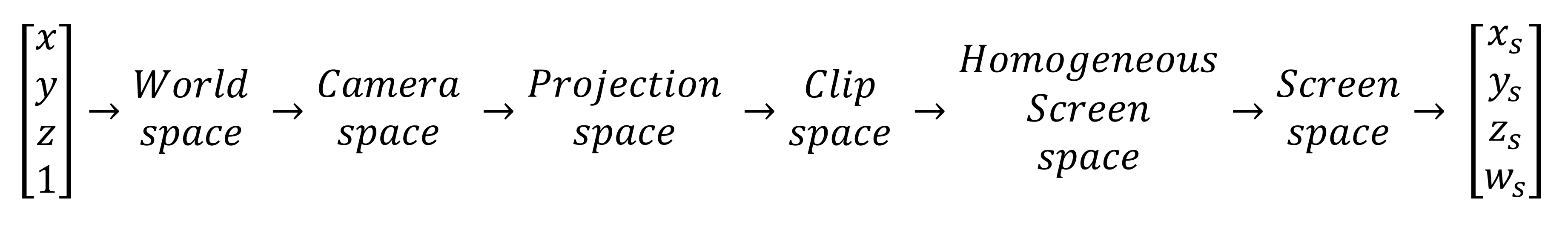
Конвейер преобразований Direct3D
В первой статье [перевод на Хабре] мы увидели, что происходит в мировом пространстве (World space): здесь при помощи различных матричных вычислений преобразуются и окрашиваются вершины. Мы пропустим следующий этап, потому что в пространстве камеры выполняется только преобразование вершин и их настройка после перемещения, чтобы опорной точкой стала камера.
Следующие этапы слишком сложны, чтобы их пропускать, потому что они абсолютно необходимы для выполнения перехода от 3D к 2D — при правильной реализации наш будет смотреть на плоский экран, но «видеть» сцену, обладающую глубиной и масштабом. Если сделать всё неправильно, то картинка окажется очень странной!
Всё дело в перспективе
Первый этап этой последовательности заключается в задании области видимости с точки зрения камеры. Для этого сначала нужно задать углы горизонтальной и вертикальной области видимости — в играх часто меняется первая, потому что у людей горизонтальное периферийное зрение развито лучше, чем вертикальное.
Мы можем разобраться в этом, посмотрев на изображение с областью зрения человека:
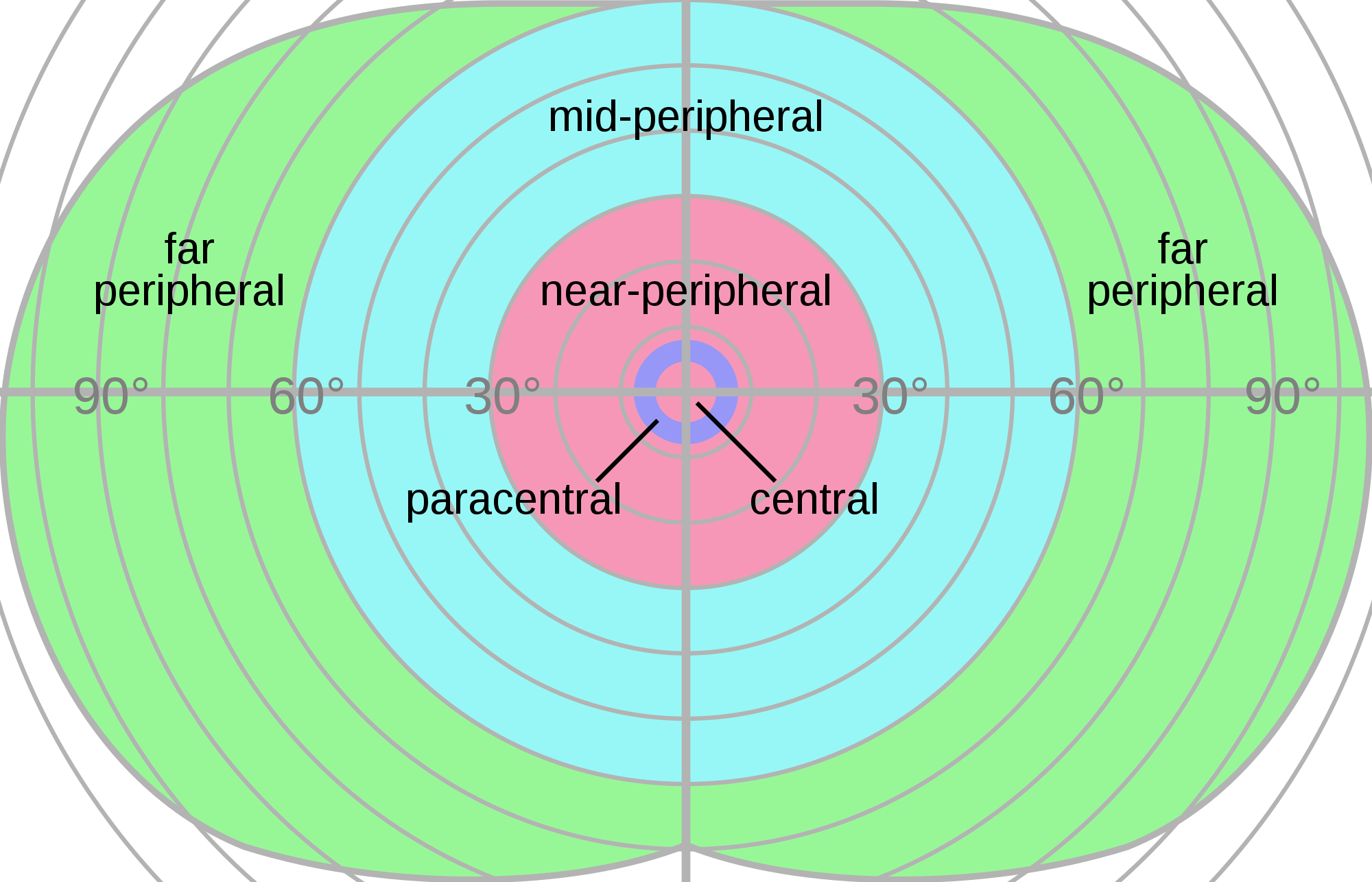
Два угла области видимости (field of view, fov) задают форму пирамиды усечения (frustum) — 3D-пирамиды с квадратным основанием, исходящей из камеры. Первый угол задаёт вертикальную fov, второй — горизонтальную; мы обозначим их символами α и β. На самом деле мы видим мир не совсем так, но с точки зрения вычислений гораздо проще работать с пирамидой усечения, а не пытаться сгенерировать реалистичный объём видимости.
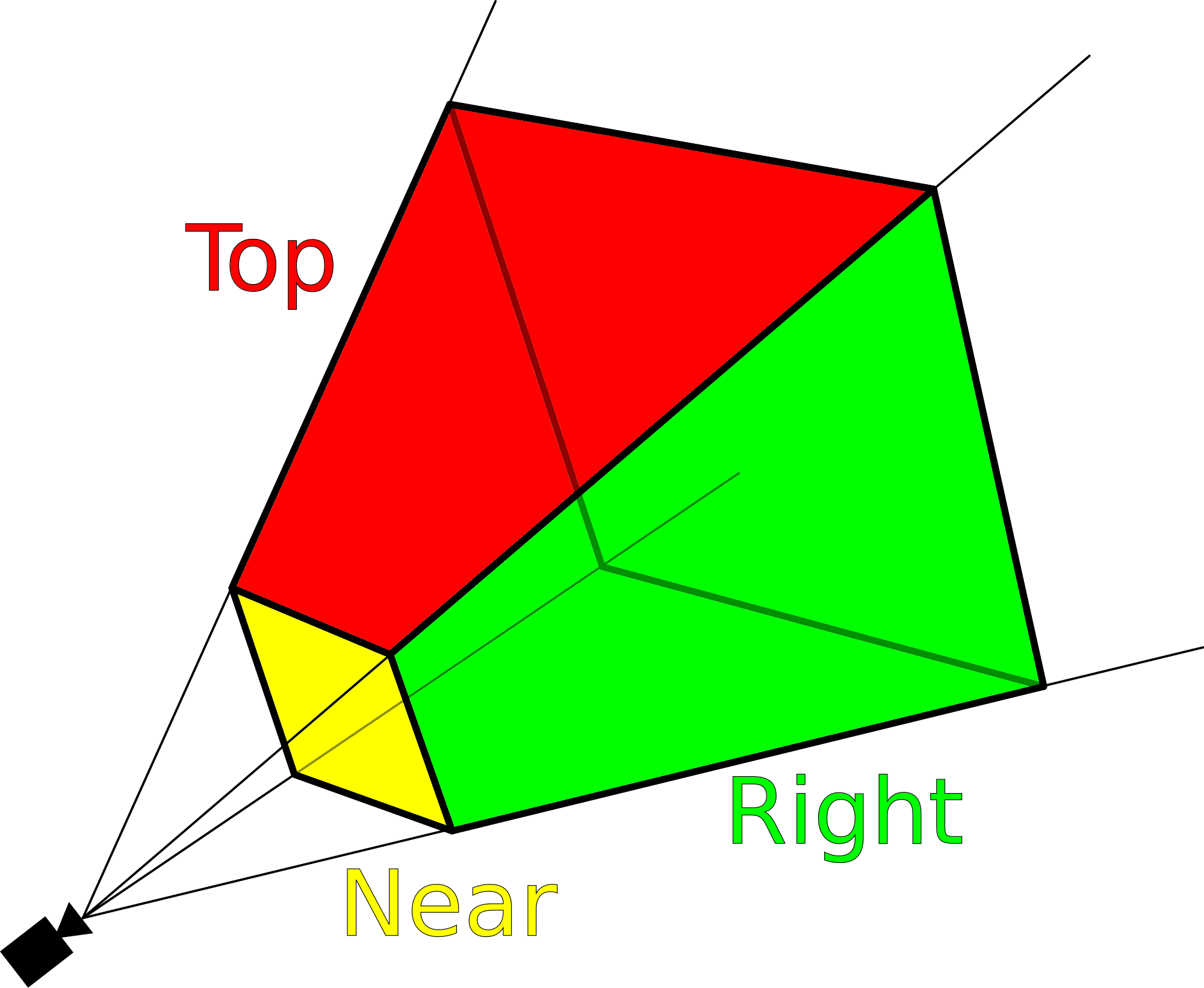
Также нужно задать ещё два параметра — расположение ближней (или передней) и дальней (задней) плоскостей усечения (clipping planes). Первая отрезает вершину пирамиды, но по сути определяет, насколько близко к позиции камеры всё отрисовывается; последняя делает то же самое, но определяет на какое расстояние от камеры будут рендериться примитивы.
Размер и расположение ближней плоскости усечения очень важны, потому что она становится тем, что называется окном просмотра (viewport). По сути, это то, что мы видим на мониторе, т.е. отрендеренный кадр, и в большинстве графических API окно просмотра отрисовывается начиная с левого верхнего угла. На показанном ниже изображении точка (a1, b2) будет точкой начала координат плоскости: ширина и высота плоскости измеряются относительно неё.
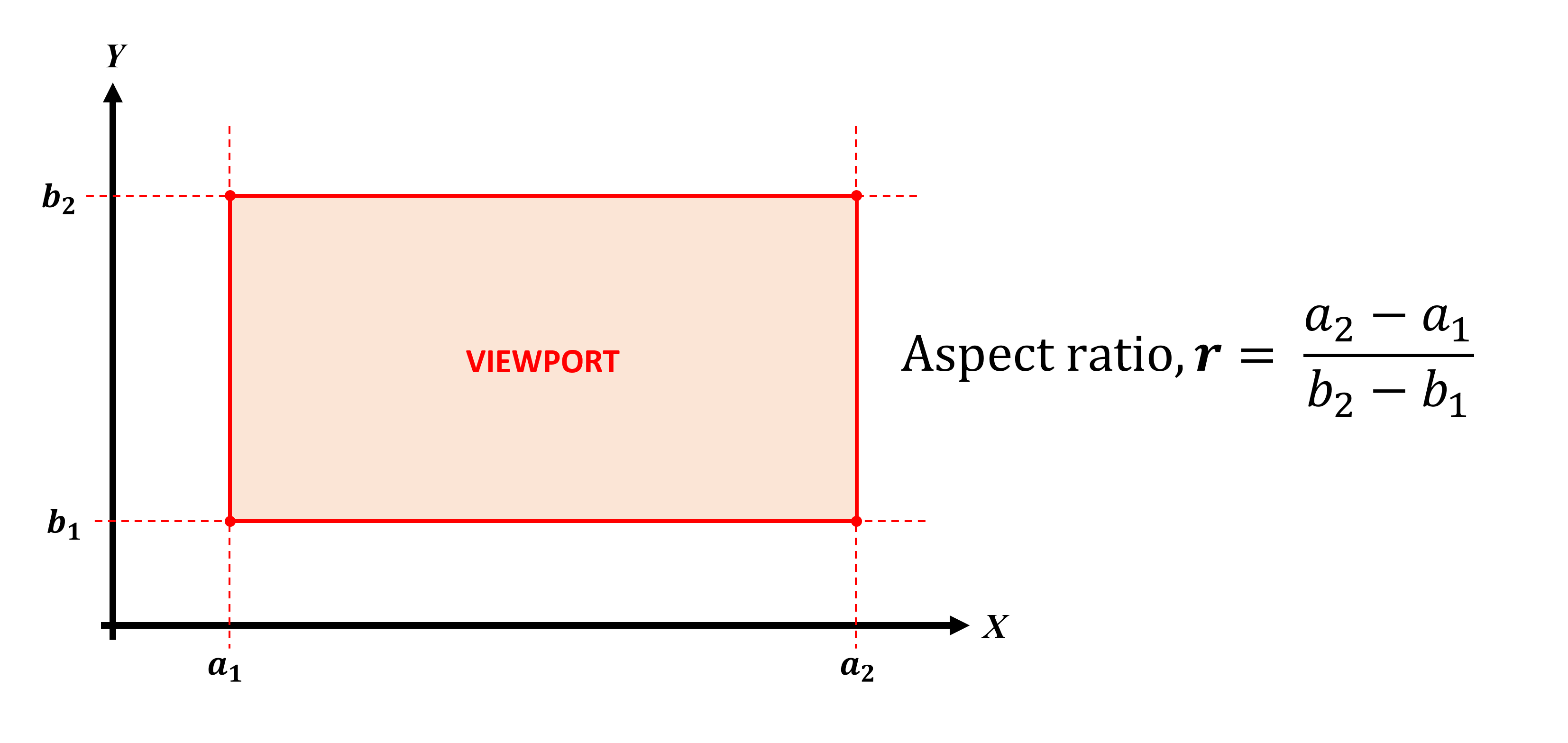
Соотношение сторон (aspect ratio) окна просмотра важно не только для отображения отрендеренного мира, но и для соответствия aspect ratio монитора. Многие годы стандартом было 4:3 (или 1.3333… в десятичном виде). Однако сегодня большинство играет в соотношении сторон 16:9 или 21:9, называемых widescreen и ultra widescreen.
Координаты каждой вершины в пространстве камеры должны быть преобразованы таким образом, чтобы все они помещались на ближней плоскости усечения, как показано ниже:

Пирамида усечения сбоку и сверху
Преобразование выполняется при помощи ещё одной матрицы, называемой матрицей перспективного проецирования (perspective projection matrix). В примере ниже для выполнения преобразований мы используем углы области видимости и позиции плоскостей усечения; однако вместо них можно применить размеры окна просмотра.
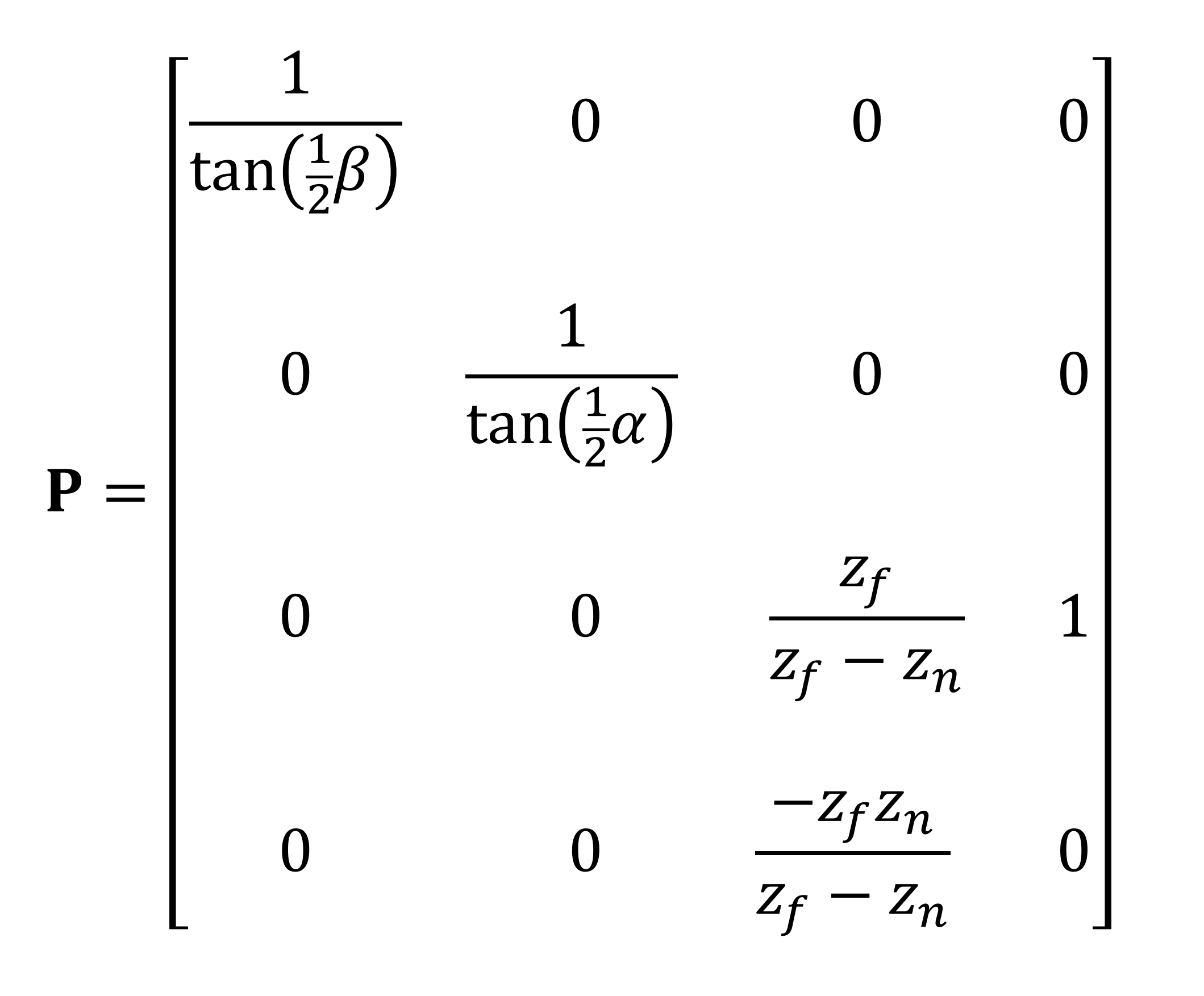
Вектор позиции вершины умножается на эту матрицу, что даёт нам новое множество преобразованных координат.
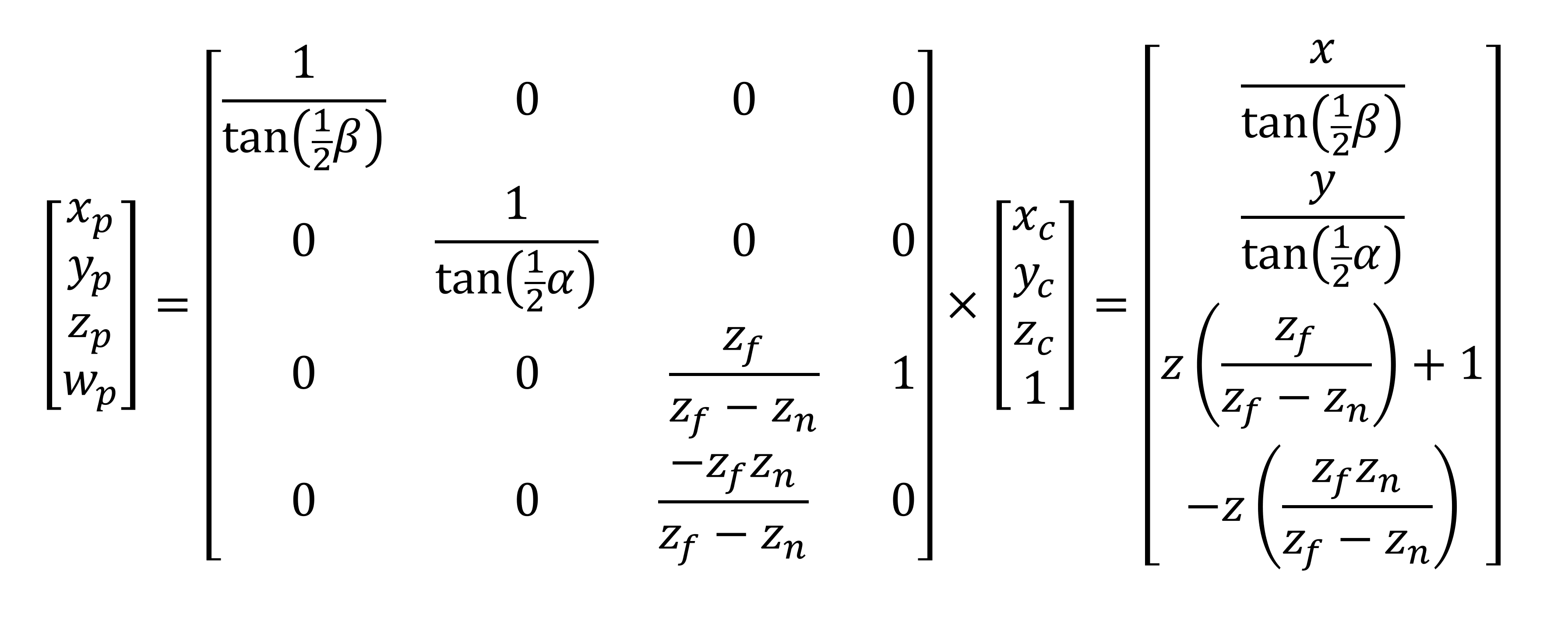
Вуаля! Теперь все вершины записаны таким образом, что исходный мир представлен как 3D-перспектива, а примитивы рядом с передней плоскостью усечения кажутся больше, чем те, которые ближе к дальней плоскости.
Хотя размер окна просмотра и углы области видимости связаны, их можно обрабатывать по отдельности. Другими словами, можно задать пирамиду усечения таким образом, чтобы получить ближнюю плоскость усечения, отличающуюся по размеру и соотношению сторон от окна просмотра. Чтобы это сделать, в цепочке операций нужен дополнительный этап, на котором вершины в ближней плоскости усечения должны быть снова преобразованы для учёта этого различия.
Однако это может привести к искажению видимой перспективы. На примере игры 2011 года Skyrim компании Bethesda мы можем увидеть, как изменение горизонтального угла области видимости β при сохранении того же соотношения сторон окна просмотра сильно влияет на сцену:

На этом первом изображении мы задали β = 75°, и сцена выглядит при этом совершенно обычной. Давайте попробуем теперь задать β = 120°:
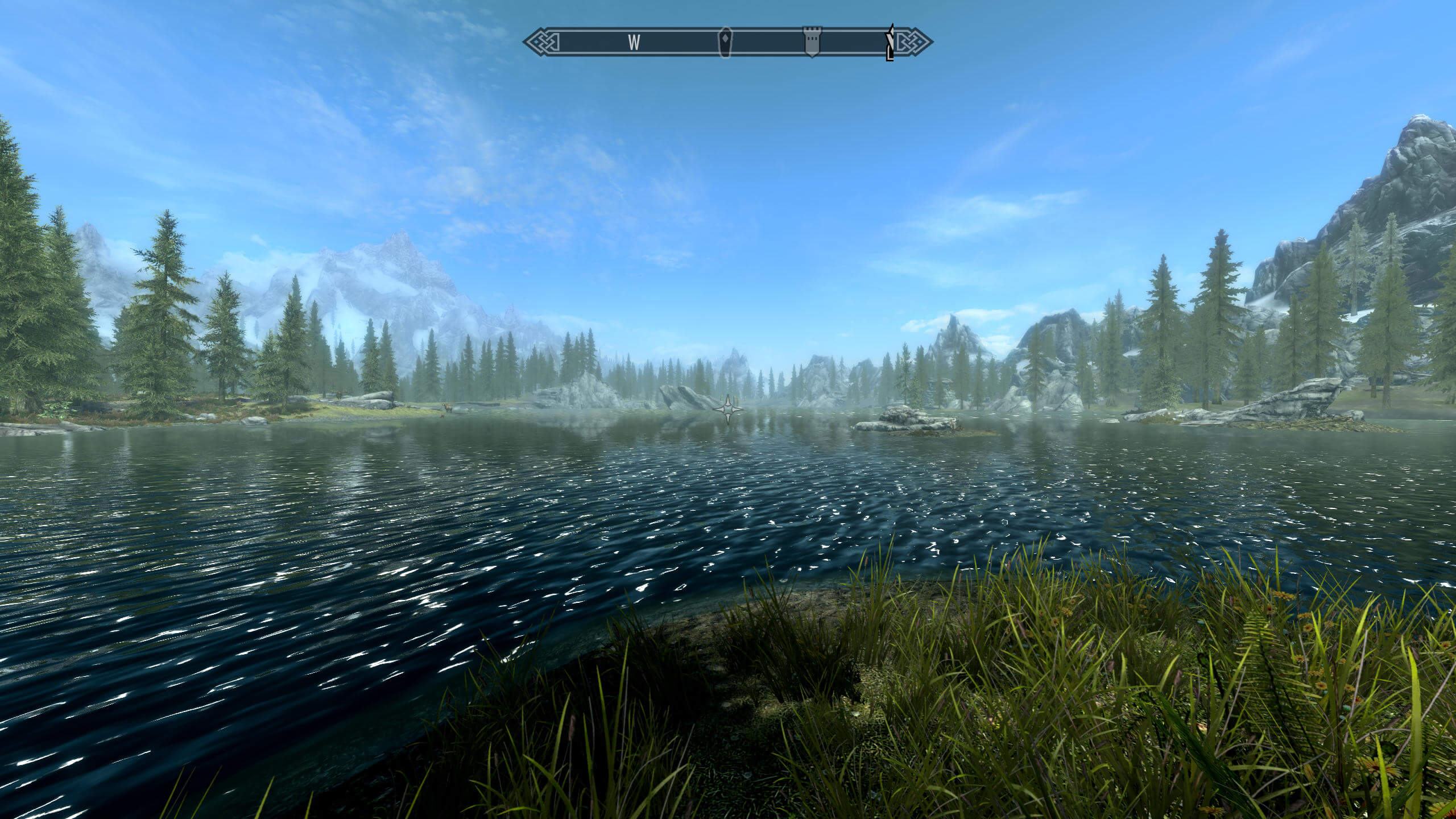
Сразу заметны два отличия — во-первых, теперь мы видим гораздо больше по бокам нашего «поля зрения»; во-вторых, объекты теперь кажутся гораздо более далёкими (особенно деревья). Однако визуальный эффект на поверхности воды теперь выглядит неправильным, потому что процесс не был рассчитан на такую область видимости.
Теперь давайте представим, что у нашего персонажа глаза инопланетянина, и зададим β = 180°!
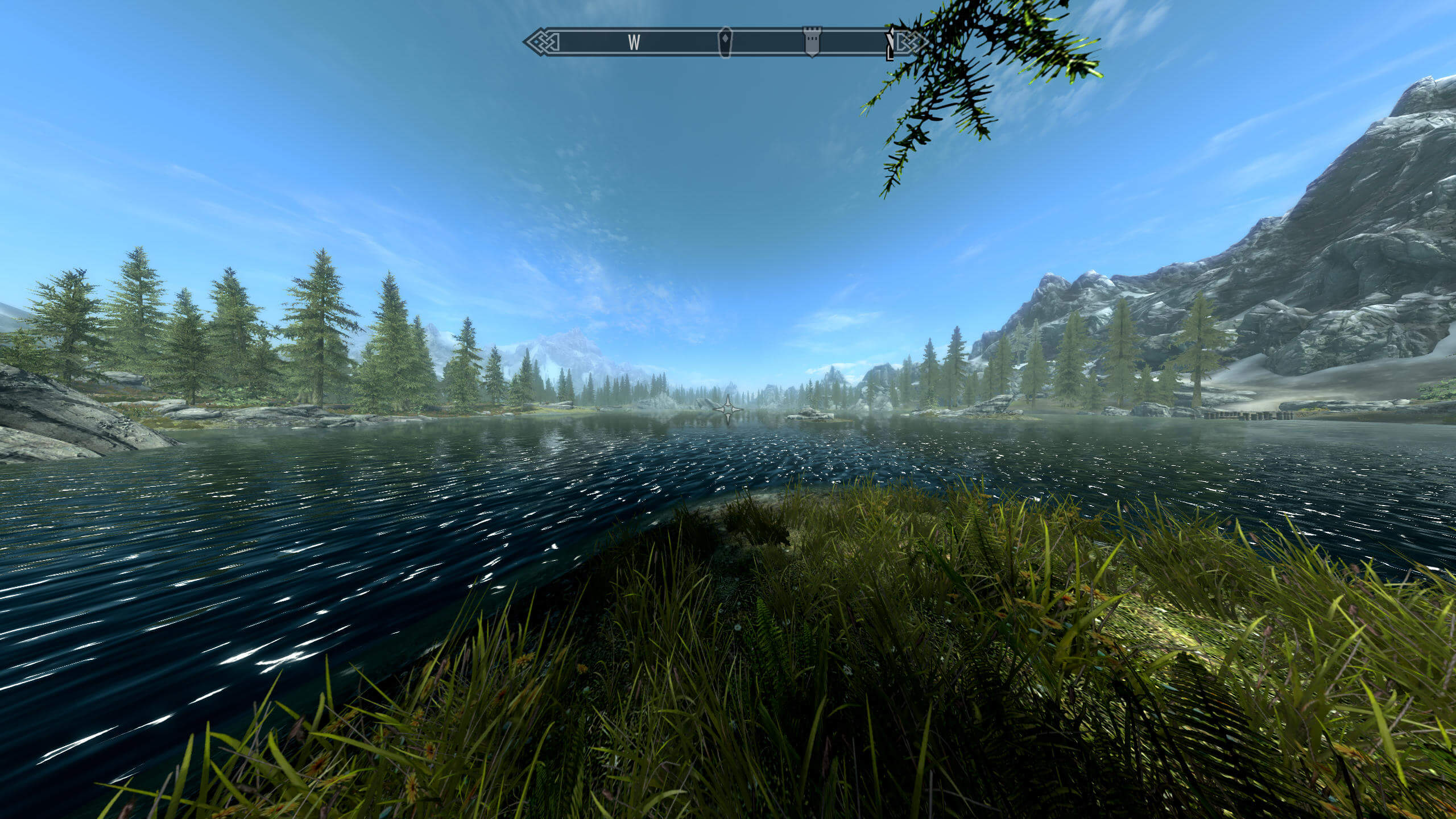
Такая область видимости создаёт почти панорамную сцену, но за это приходится расплачиваться серьёзной величиной искажения объектов, рендерящихся по краям. Это опять-таки произошло из-за того, что дизайнеры игры не предусматривали такой ситуации и не создавали ресурсы и визуальные эффекты игры для такого угла обзора (стандартное значение примерно равно 70°).
Может показаться, что на показанных выше изображениях камера переместилась, но это не так — единственное изменение заключается в модификации пирамиды усечения, которая в свою очередь изменила размеры ближней плоскости усечения. На каждом изображении соотношение сторон окна просмотра остаётся одинаковым, поэтому к вершинам применена матрица масштабирования, чтобы в него всё помещалось.
Так ты остаёшься или уходишь?
После выполнения преобразований на этапе проецирования мы переходим к тому, что называется пространством усечения (clip space). Хотя это делается после проецирования, проще показать, что происходит, если мы выполним операции заранее:
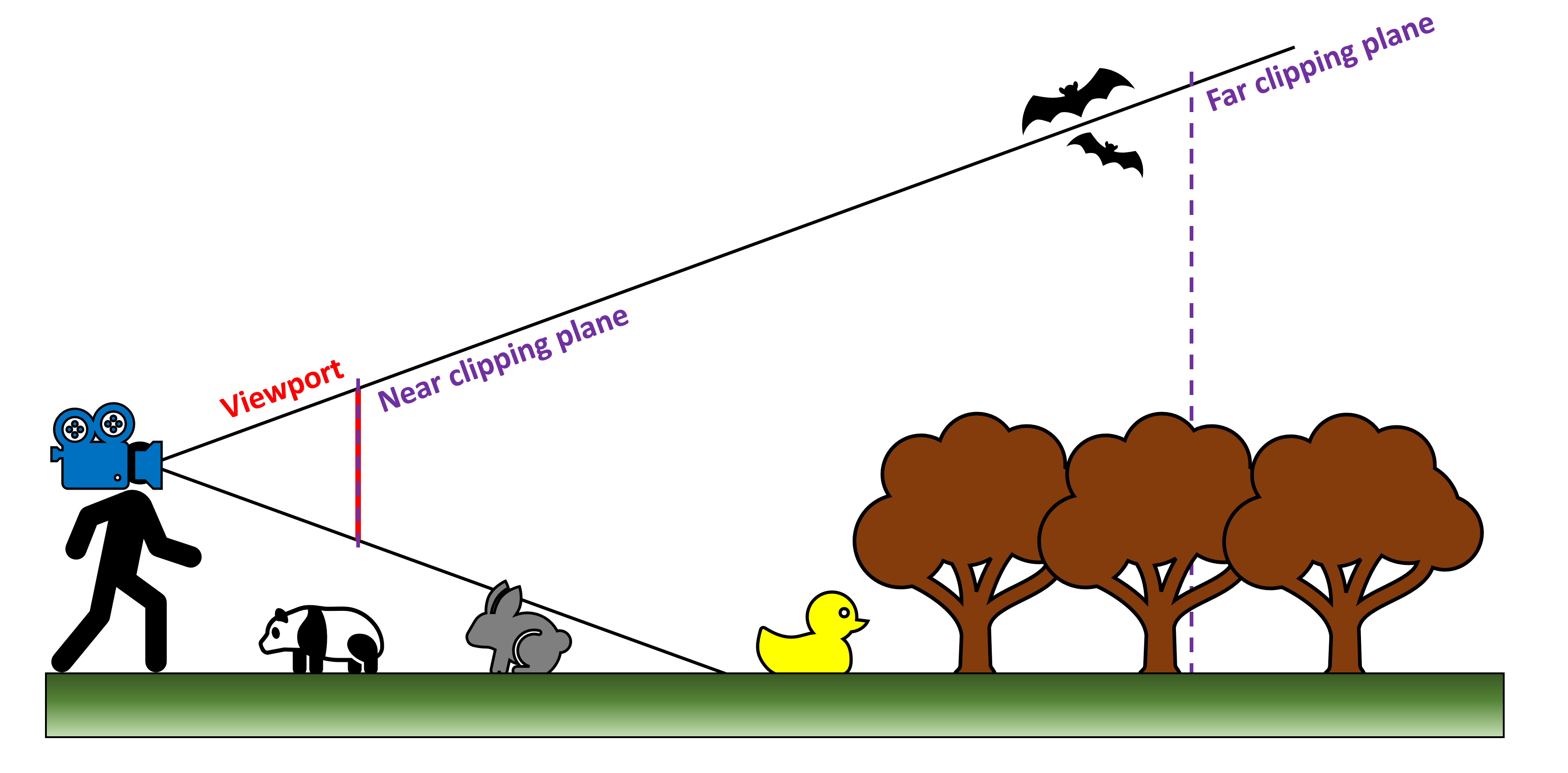
На рисунке выше мы видим, что у резиновой уточки, одной из летучих мышей и части деревьев треугольники находятся внутри пирамиды усечения; однако другая летучая мышь и самое дальнее дерево находятся вне пределов пирамиды усечения. Хотя вершины, из которых состоят эти объекты, уже были обработаны, в окне просмотра мы их не увидим. Это означает, что они усечены (clipped).
При усечении по пирамиде (frustum clipping) все примитивы за пределами пирамиды усечения полностью удаляются, а лежащие на границах преобразуются в новые примитивы. Усечение не очень сильно повышает производительность, потому что все эти невидимые вершины уже были обработаны до этого этапа в вершинных шейдера и т.п. При необходимости весь этап усечения даже можно полностью пропустить, но эта возможность поддерживается не всеми API (например, стандартный OpenGL не позволит пропустить его, однако это можно сделать при помощи расширения API).
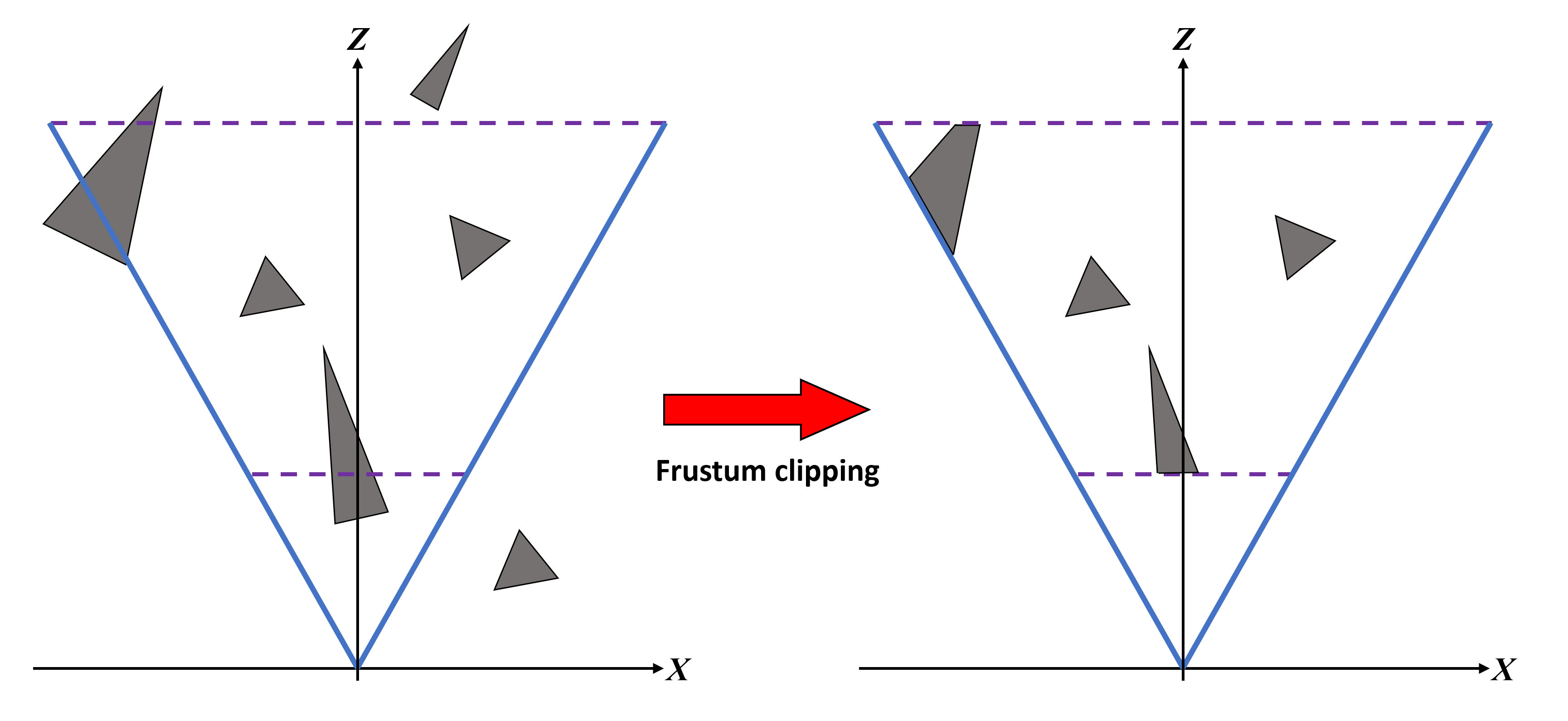
Стоит заметить, что позиция дальней плоскости усечения в играх не всегда равна расстоянию отрисовки (draw distance), потому что последней управляет сам игровой движок. Также движок выполняет отсечение по пирамиде (frustum culling) — он запускает код, определяющий будет ли объект отрисовываться в пределах пирамиды усечения и будет ли он влиять на видимые объекты; если ответ отрицательный, то объект не передаётся на рендеринг. Это не то же самое, что усечение по пирамиде (frustrum clipping), потому что при нём тоже отбрасываются примитивы вне пирамиды, но они уже прошли этап обработки вершин. При отсечении (culling) они вообще не обрабатываются, что экономит довольно много ресурсов.
Мы выполнили все преобразования и усечение, и кажется, что вершины наконец готовы к следующему этапу в последовательности рендеринга. Но на самом деле это не так, потому что все вычисления, проводимые на этапе обработки вершин и в операциях преобразования из мирового пространства в пространство усечения, должны выполняться в однородной системе координат (т.е. каждая вершина имеет 4 компоненты, а не 3). Однако окно просмотра полностью двухмерно, то есть API ожидает, что информация вершин содержит только значения для x, y (хотя значение глубины z и сохраняется).
Чтобы избавиться от четвёртой компоненты, выполняется перспективное деление (perspective division), при котором каждая компонента делится на значение w. Эта операция ограничивает x и y интервалом возможных значений [-1,1], а z — интервалом [0,1]. Они называются нормализованными координатами устройства (normalized device coordinates) (NDC).
Если вы хотите подробнее разобраться с тем, что мы только что объяснили, и вам нравится математика, то прочитайте превосходный туториал по этой теме Сон Хо Ана. А теперь давайте превратим эти вершины в пиксели!
Осваиваем растеризацию
Как и в случае с преобразованиями, мы рассмотрим правила и процессы, используемые для превращения окна просмотра в сетку пикселей, на примере Direct3D. Эта таблица напоминает электронную таблицу Excel со строками и столбцами, в которой каждая ячейка содержит различные значения данных (такие как цвет, значения глубины, координаты текстур и т.п.). Обычно эта сетка называется растровым изображением (raster), а процесс её генерации — растеризацией (rasterization). В статье 3D rendering 101 мы упрощённо рассматривали эту процедуру:
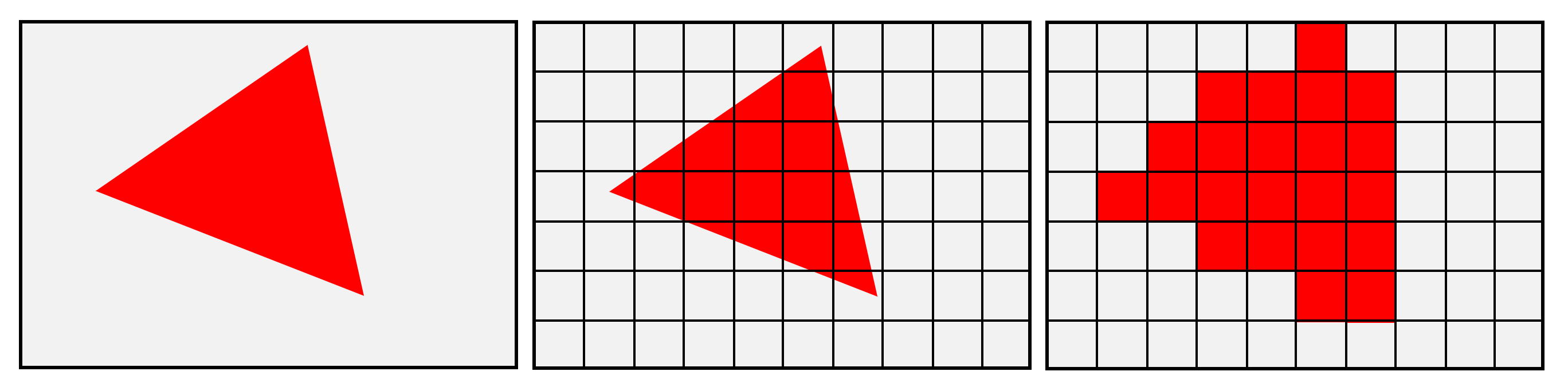
Изображение выше создаёт впечатление, что примитивы просто разрезаются на мелкие блоки, но на самом деле операций намного больше. Самый первый этап — это определение того, обращён ли примитив в сторону камеры — например, на показанном выше изображении с пирамидой усечения примитивы, из которых состоит задняя часть серого кролика, не будут видимыми. Поэтому хотя они присутствуют в окне просмотра, рендерить их не нужно.
Мы можем приблизительно представить, как это выглядит, посмотрев на схему ниже. Куб прошёл различные преобразования для помещения 3D-модели в 2D-пространство экрана и с точки зрения камеры часть граней куба не видна. Если мы считать, что все поверхности непрозрачны, тогда часть этих примитивов можно игнорировать.

Слева направо: мировое пространство > пространство камеры > пространство проецирования > экранное пространство
В Direct3D это можно реализовать, сообщив системе, каким будет состояние рендера, и эта инструкция даст ей понять, что нужно удалить (отсечь) стороны каждого примитива, смотрящие вперёд или назад (или не отсекать совсем, например, в каркасном (wireframe) режиме). Но как она узнает, какие из сторон смотрят вперёд или назад? Когда мы рассматривали математику обработки вершин, то видели, что треугольники (или скорее вершины) имеют векторы нормалей, сообщающие системе, в какую сторону он смотрит. Благодаря этой информации можно выполнить простую проверку, и если примитив её не пройдёт, то он удаляется из цепочки рендеринга.
Теперь настало время применения пиксельной сетки. Это снова неожиданно сложный процесс, потому что система должна понять, находится ли пиксель внутри примитива — полностью, частично или вообще не внутри. Для этого выполняется процесс проверки покрытия (coverage testing). На рисунке ниже показано, как растеризируются треугольники в Direct3D 11:
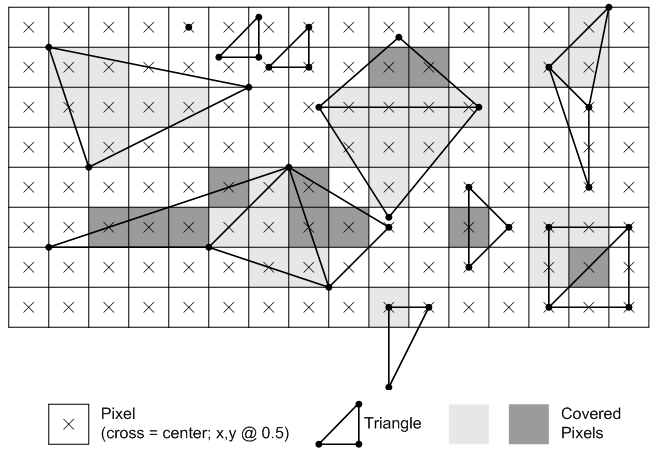
Правило довольно простое: пиксель считается находящимся внутри треугольника, если центр пикселя проходит проверку, которую Microsoft называет правилом «верхнего левого угла» («top left» rule). «Верхний» относится к проверке горизонтальной линии; центр пикселя должен находиться на этой линии. «Левый» относится к негоризонтальным линиям, и центр пикселя должен находиться слева от такой линии. Существуют и другие правила, относящиеся к непримитивам, например, простым отрезкам и точкам, а при использовании мультисэмплирования (multisampling) в правилах появляются дополнительные условия if.
Если внимательно присмотреться к документации Microsoft, то можно увидеть, что создаваемые пикселями фигуры не очень похожи на исходные примитивы. Так происходит потому, что пиксели слишком велики для создания реалистичного треугольника — растровое изображение содержит недостаточно данных об исходных объектах, что вызывает явление под названием алиасинг (aliasing).
Давайте рассмотрим алиасинг на примере UL Benchmark 3DMark03:
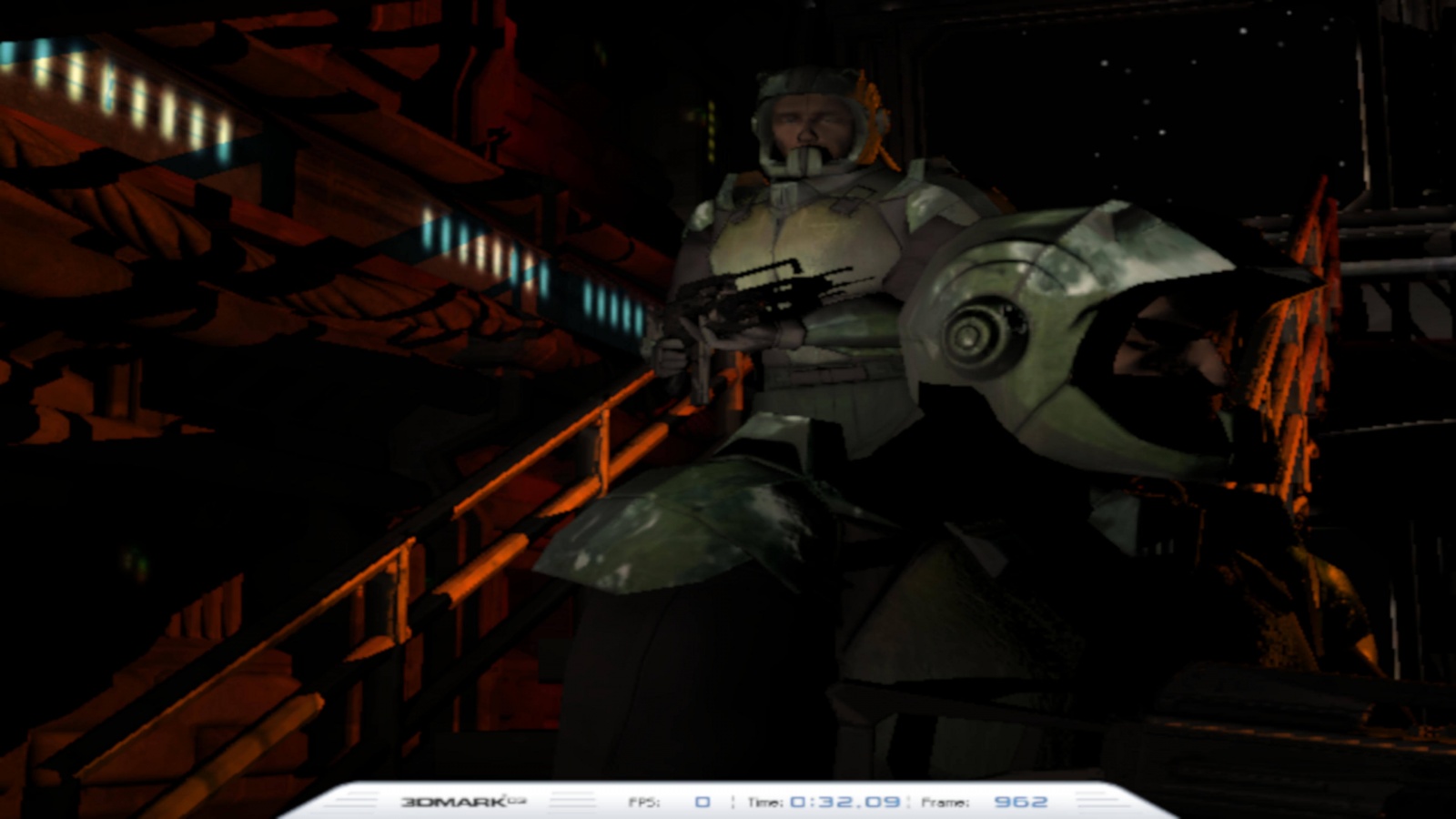
Растеризация размером 720 x 480 пикселей
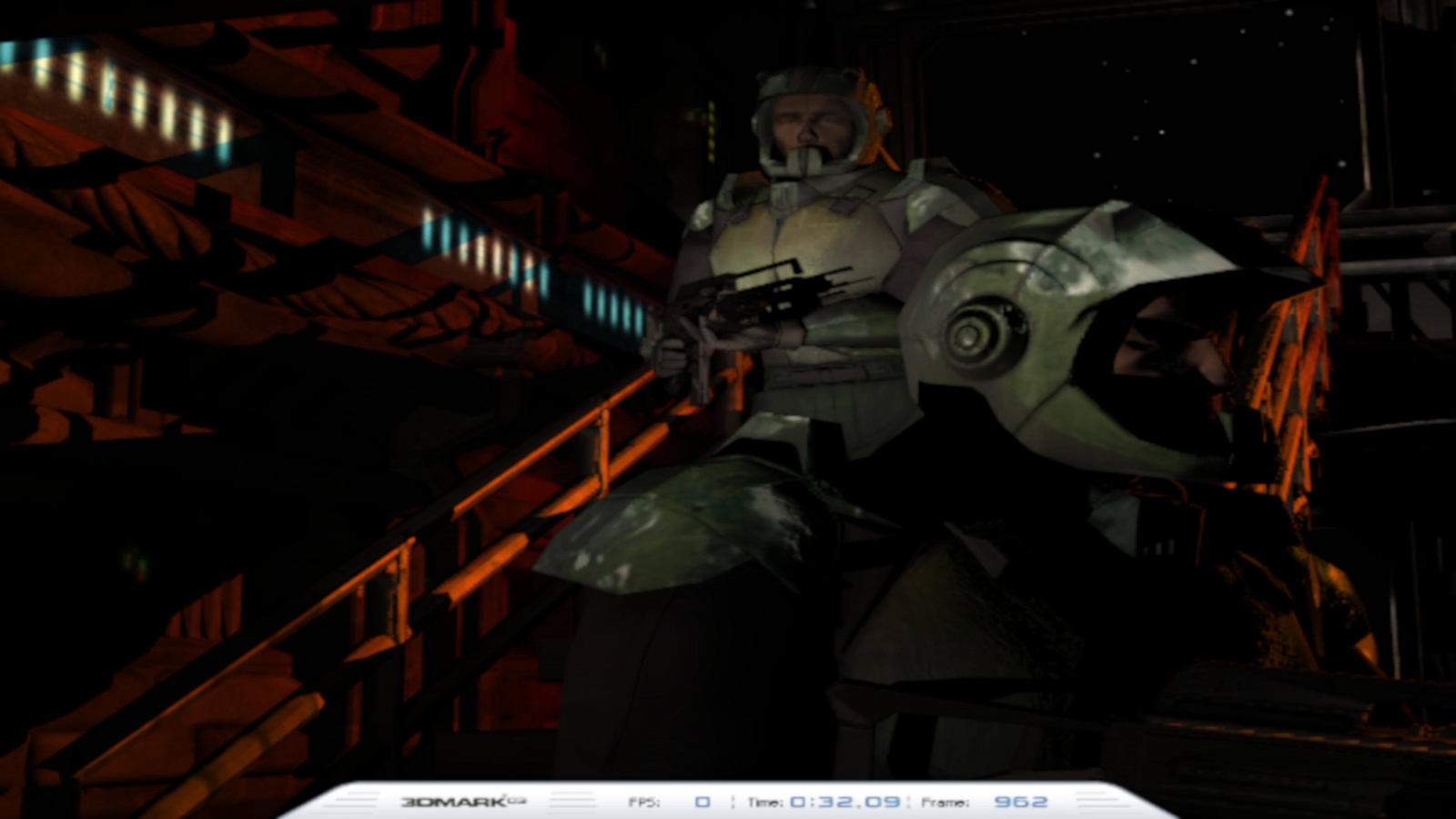
На первом изображении растровое изображение имеет очень низкое разрешение — 720 на 480 пикселей. Алиасинг чётко заметен на перилах и тени, отбрасываемой оружием верхнего солдата. Сравните это с результатом, получаемым при растеризации с увеличенным в 24 раза количеством пикселей:

Растеризация размером 3840 x 2160 пикселей
Здесь мы видим, что алиасинг на перилах и тени совершенно исчез. Похоже, что следует всегда использовать большое растровое изображение, но размеры сетки должны поддерживаться монитором, на котором будет отображаться кадр. А с учётом того, что все эти пиксели нужно обработать, очевидно, что возникнет снижение производительности.
Здесь может помочь мультисэмплирование. Вот как оно работает в Direct3D:
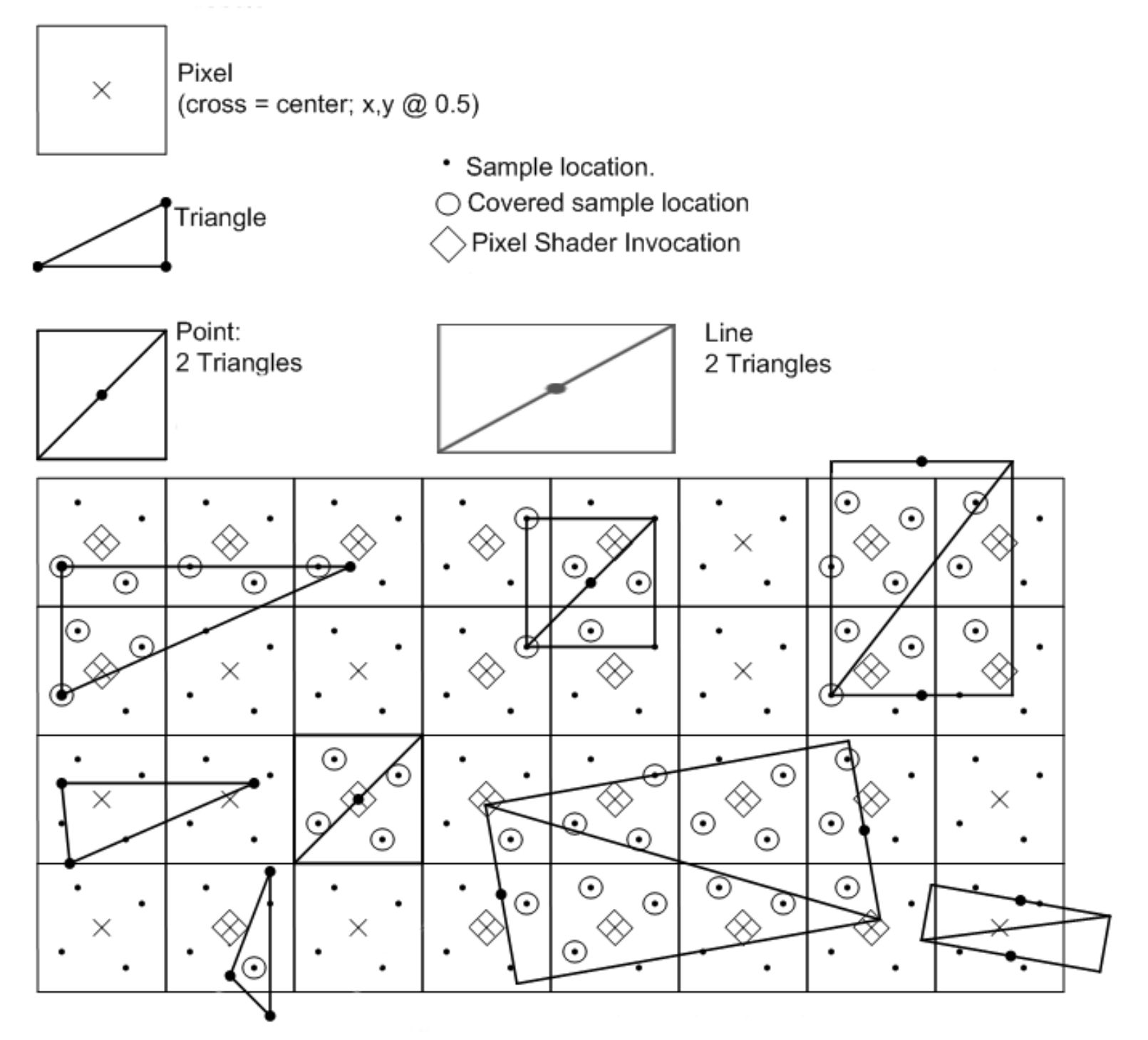
Вместо того, чтобы проверять соответствие центра пикселя правилам растеризации, проверяются несколько точек внутри каждого пикселя (называемых субпиксельными сэмплами или субсэмплами), и если какие-то из них удовлетворяют требованиям, то они образуют часть фигуры. Может показаться, что здесь нет никакой выгоды и алиасинг даже усиливается, но при использовании мультисэмплирования информация о том, какие субсэмплы покрыты примитивом, и результаты обработки пикселей сохраняются в буфер в памяти.
Этот буфер затем используется для смешения данных субсэмплов и пикселей таким образом, чтобы края примитива были менее рваными. Подробнее мы рассмотрим алиасинг в другой статье, но пока этой информации нам достаточно, чтобы понять, что может делать мультисэмплирование, когда используется для растеризации слишком малого количества пикселей:
Как видите, величина алиасинга на краях разных фигур значительно снизилась. Растеризация с большим разрешением определённо лучше, но снижение производительности может подтолкнуть вас с использованию мультисэмплирования.
Также в процессе растеризации выполняется проверка перекрытия (occlusion testing). Она необходима, потому что окно просмотра будет заполнено наложенными друг на друга примитивами — например, на рисунке выше смотрящие вперёд треугольники, составляющие солдата, стоящего на переднем плане, перекрывают те же треугольники другого солдата. Кроме проверки того, покрывает ли примитив пиксель, можно также сравнить относительные глубины, и если одна поверхность находится за другой, то её нужно удалить из оставшегося процесса рендеринга.
Однако если ближний примитив прозрачен, то дальний останется видимым, хотя и не пройдёт проверку перекрытия. Именно поэтому почти все 3D-движки выполняют проверки перекрытия до отправки данных в GPU и вместо этого создают нечто под названием z-буфер, являющийся частью процесса рендеринга. Здесь кадр создаётся обычным образом, но вместо сохранения готовых цветов пикселей в памяти GPU сохраняет только значения глубин. Позже их можно использовать в шейдерах для проверки видимости и с большим контролем и точностью аспектов, касающихся перекрытия объектов.

На показанном выше изображении чем темнее цвет пикселя, тем ближе объект к камере. Кадр рендерится один раз для создания z-буфера, а затем рендерится снова, но на этот раз во время обработки пикселей запускается шейдер, проверяющий их на значения в z-буфере. Если он невидим, то цвет пикселя не записывается в буфер готового кадра.
Пока нашим основным последним этапом будет интерполяция атрибутов вершин — в исходной упрощённой схеме примитив был полным треугольником, но не забывайте, что окно просмотра заполняется только углами фигур, а не самими фигурами. То есть система должна определить, какие цвет, глубина и текстура примитива должны находиться между вершинами, и эта операция называется интерполяцией. Как вы уже догадались, это ещё одно вычисление, и оно не такое уж простое.
Несмотря на то, что растеризованный экран представлен в 2D, структуры внутри него представляют собой 3D-перспективу. Если бы линии действительно были двухмерными, то для вычисления цветов и прочего мы бы могли использовать простое линейное уравнение, потому что мы переходим от одной вершины к другой. Но из-за 3D-аспекта сцены интерполяция должна учитывать эту перспективу; чтобы подробнее узнать об этом процессе, прочитайте превосходную статью Саймона Юна.
Итак, задача выполнена — так 3D-мир вершин превращается в 2D-сетку разноцветных блоков. Но мы ещё не совсем закончили.
Спереди назад (за некоторыми исключениями)
Прежде чем мы завершим рассматривать растеризацию, нужно рассказать о порядке последовательности рендеринга. Мы не говорим о том этапе, где, например, в последовательности обработки появляется тесселяция; мы имеем в виду порядок обработки примитивов. Объекты обычно обрабатываются в порядке, в котором они находятся в буфере индексов (блоке памяти, сообщающем системе, как сгруппированы между собой вершины) и это может значительно влиять на способ обработки прозрачных объектов и эффектов.
Причина этого сводится к тому, что примитивы обрабатываются по одному за раз, и если сначала отрендерить находящиеся впереди, то все находящиеся за ними будут невидимыми (именно здесь в действие вступает отсечение перекрытий (occlusion culling)) и могут быть выброшены из процесса (помогая сохранять производительность). Обычно это называется рендерингом "спереди назад", и для этого процесса буфер индексов должен быть упорядочен таким образом.
Однако если некоторые из этих примитивов прямо перед камерой прозрачны, то рендеринг спереди назад приведёт к потере объектов, находящихся за прозрачным. Одно из решений заключается в рендеринге сзади вперёд, при котором прозрачные примитивы и эффекты рассчитываются последними.
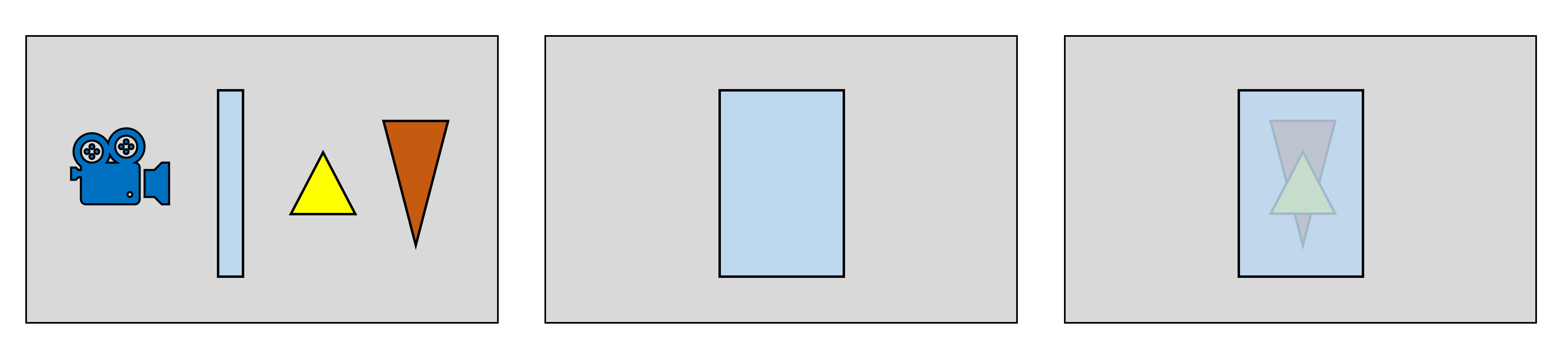
Слева направо: порядок в сцене, рендеринг спереди назад, рендеринг сзади вперёд
То есть во всех современных играх рендеринг выполняется сзади вперёд? Как бы не так — не забывайте, что рендеринг каждого отдельного примитива приведёт к гораздо большему снижению производительности по сравнению с рендерингом только того, что мы видим. Существуют другие способы обработки прозрачных объектов, но в общем случае идеального решения, подходящего к любой системе, нет, и каждую ситуацию нужно рассматривать отдельно.
По сути, это даёт нам понять основные плюсы и минусы растеризации — на современном оборудовании это быстрый и эффективный процесс, но он всё ещё является приближенным отображением того, что мы видим. В реальном мире каждый объект может поглощать, отражать, а иногда и преломлять свет, и всё это влияет на конечный вид отображаемой сцены. Разделив мир на примитивы и выполняя рендеринг только их части, мы получаем быстрый. но очень приблизительный результат.
Вот если бы существовал ещё какой-то способ…
Другой способ есть: ray tracing!
Почти пятьдесят лет назад компьютерный учёный по имени Артур Эппел работал над системой для рендеринга изображений на компьютере, в которой из камеры испускался по прямой линии до столкновения с объектом один луч света. После столкновения свойства материала (его цвет, отражающая способность и т.п.) изменяли яркость луча света. На каждый пиксель в отрендеренном изображении приходился один испущенный луч, а алгоритм выполнял цепочку вычислений для определения цвета пикселя. Процесс Эппела называют ray casting.
Примерно десять лет спустя ещё один учёный по имени Джон Уиттед разработал математический алгоритм, реализующий процесс Эппела, но при столкновении луча с объектом он генерировал дополнительные лучи, расходящиеся в разных направлениях, зависящих от материала объекта. Так как эта система генерировала новые лучи при каждом взаимодействии с объектами, алгоритм по своей природе был рекурсивным и вычислительно гораздо более сложным; однако он имел значительное преимущество по сравнению с методикой Эппела, поскольку мог правильно учитывать отражения, преломления и тени. Эту процедуру назвали трассировкой лучей (ray tracing) (строго говоря, это обратная трассировка лучей, потому что мы следуем за лучом из камеры, а не от объектов) и с тех пор она стала священным Граалем для компьютерной графики и фильмов.
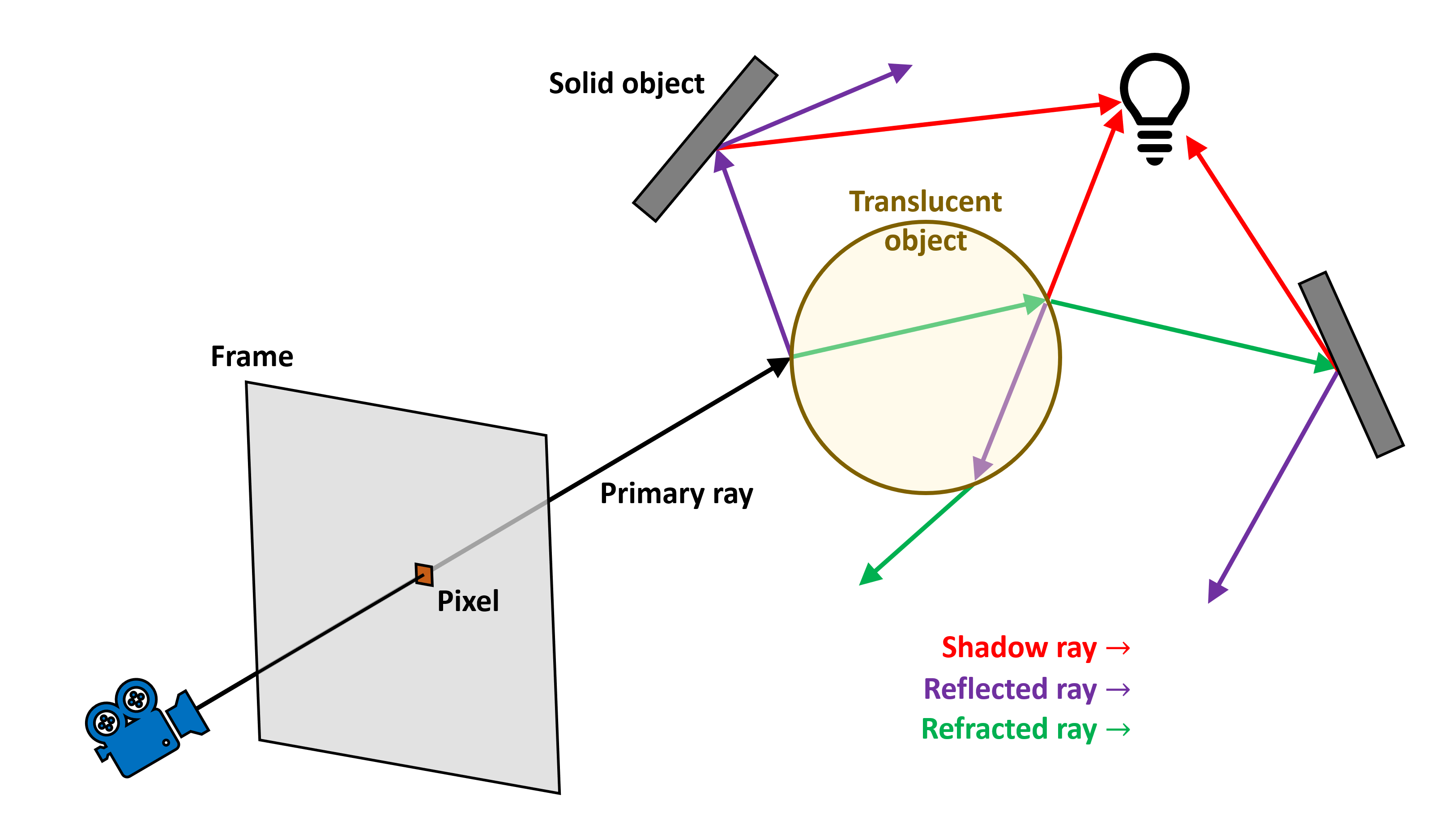
Из показанного выше изображения можно понять, как работает алгоритм Уиттеда. Для каждого пикселя в кадре из камеры испускается один луч и перемещается, пока не достигнет поверхности. В данном примере поверхность просвечивающая, поэтому свет может отражаться и преломляться сквозь неё. В обоих случаях генерируются вторичные лучи, которые перемещаются, пока не столкнутся с поверхностью. Также генерируются новые вторичные лучи для учёта цвета источников освещения и создаваемых ими теней.
Рекурсивность процесса заключается в том, что вторичные лучи могут генерироваться каждый раз когда новый испущенный луч пересекается с поверхностью. Это может быстро выйти из-под контроля, поэтому количество генерируемых вторичных лучей всегда ограничивается. После завершения пути луча вычисляется цвет в каждой конечной точке на основании свойств материала этой поверхности. Это значение затем передаётся по лучу предыдущему, изменяя цвет для этой поверхности, и так далее, пока мы не достигнем начальной точки первичного луча, а именно пикселя в кадре.
Такая система может быть чрезвычайно сложной и даже простые сцены могут генерировать большой объём вычислений. К счастью, существуют трюки, упрощающие работу — во-первых, можно использовать оборудование, специально спроектированное для ускорения этих математических операций, аналогично тому, как это происходит с матричной математикой в обработке вершин (подробнее об этом чуть позже). Ещё один важнейший трюк — это попытка ускорения процесса определения объекта, в который попал луч, и точного места их пересечения — если объект состоит из множества треугольников, то эта задача может быть на удивление трудной:

Источник: Трассировка лучей в реальном времени при помощи Nvidia RTX
Вместо того, чтобы проверять каждый отдельный треугольник в каждом объекте перед выполнением трассировки лучей генерируется список ограничивающих объёмов (bounding volumes, BV) — это обычные параллелепипеды, описывающие объект. Для различных структур внутри объекта циклически создаются меньшие ограничивающие объёмы.
Например, первым BV будет весь кролик целиком. Следующая пара будет описывать его голову, ноги, тело, хвост и т.д.; каждый из объёмом в свою очередь будет ещё одной коллекцией объёмов для меньших структур головы, тела и т.д., а последний уровень объёмов будет содержать небольшое количество треугольников для проверки. Все эти объёмы часто выстраиваются в упорядоченный список, (называемый BV hierarchy или BVH); благодаря этому система каждый раз проверяет относительно небольшое количество BV:

Хотя использование BVH, строго говоря, не ускоряет саму трассировку лучей, генерация иерархии и требуемый последующий алгоритм поиска в общем случае гораздо быстрее, чем проверка наличия пересечения одного луча с одним из миллионов треугольников в 3D-мире.
Сегодня такие программы, как Blender и POV-ray используют трассировку лучей с дополнительными алгоритмами (такими как photon tracing и radiosity) для генерации очень реалистичных изображений:

Может возникнуть очевидный вопрос: если трассировка лучей так хороша, почему же она не используются повсюду? Ответ лежит в двух областях: во-первых, даже простая трассировка лучей создаёт миллионы лучей, которые нужно вычислять снова и снова. Система начинает всего с одного луча на пиксель экрана, то есть при разрешении 800 x 600 она генерирует 480 000 первичных лучей, а затем каждый из них генерирует множество вторичных лучей. Это очень сложная работа даже для современных настольных PC. Вторая проблема заключается в том, что простая трассировка лучей не особо реалистична и для её правильной реализации нужна целая куча дополнительных очень сложных уравнений.
Даже на современном оборудовании объём работы в 3D-играх недостижим для реализации в реальном времени. В статье 3D rendering 101 мы видели, что бенчмарку трассировки лучей для создания одного изображения с низким разрешением требуются десятки секунд.
Как же первый Wolfenstein 3D выполнял ray casting ещё в 1992 году и почему игры наподобие Battlefield V и Metro Exodus, выпущенные в 2019 году, предлагают возможности трассировки лучей? Они выполняют растеризацию или трассировку лучей? Понемногу и того, и другого.
Гибридный подход для современности и будущего
В марте 2018 года Microsoft объявила о выпуске нового расширения API для Direct3D 12 под названием DXR (DirectX Raytracing). Это был новый графический конвейер, дополняющий стандартные конвейеры растеризации и вычислений. Дополнительная функциональность обеспечивалась добавлением шейдеров, структур данных и так далее, но не требовала аппаратной поддержки, кроме той, которая уже была необходима для Direct3D 12.

На той же Game Developers Conference, на которой Microsoft рассказывала о DXR, Electronic Arts говорила о своём Pica Pica Project — эксперименте с 3D-движком, использующим DXR. Компания показала, что трассировку лучей можно использовать, но не для рендеринга всего кадра. В основной части работы используются традиционные техники растеризации и вычислительных шейдеров, а DXR применяется в специфических областях. То есть количество генерируемых лучей намного меньше, чем оно было бы для целой сцены.

Такой гибридный подход использовался в прошлом, хотя и в меньшей степени. Например, в Wolfenstein 3D использовался ray casting для рендерига кадра, однако он выполнялся с одним лучом на столбец пикселей, а не на пиксель. Это всё равно может показаться впечатляющим, если только не вспоминать, что игра работала с разрешением 640 x 480 [прим. пер.: на самом деле 320 x 200], то есть одновременно испускалось не больше 640 лучей.
Графические карты начала 2018 года наподобие AMD Radeon RX 580 или Nvidia GeForce 1080 Ti удовлетворяли требованиям DXR, но даже при их вычислительных возможностях существовали опасения, что они будут недостаточно мощны для того, чтобы использование DXR имело смысл.
Ситуация изменилась в августе 2018 года, когда Nvidia выпустила свою новейшую архитектуру GPU под кодовым названием Turing. Важнейшей особенностью этого чипа стало появление так называемых RT Cores: отдельных логических блоков для ускорения вычислений пересечения луч-треугольник и прохождения иерархии ограничивающих объёмов (BVH). Эти два процесса — затратные по времени процедуры для определения точек взаимодействия света с треугольниками, составляющими объекты сцены. С учётом того, что RT Cores были уникальными блоками процессора Turing, доступ к ним мог выполняться только через проприетарный API Nvidia.
Первой игрой с поддержкой этой функции стала Battlefield V компании EA. Когда мы протестировали в ней DXR, то были впечатлены улучшением отражений в воды, на траве и металлах, а также соответствующим снижением производительности:
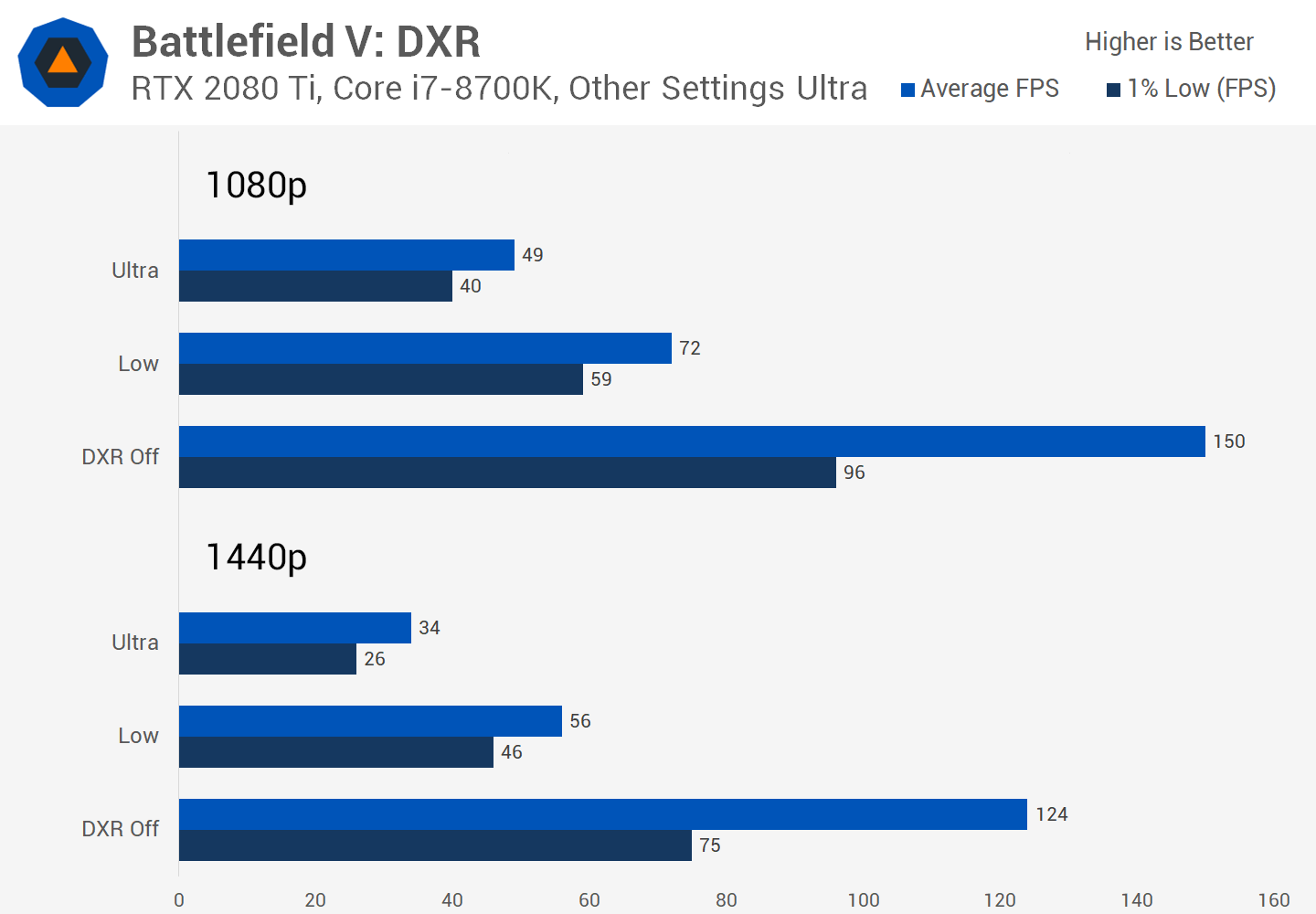
Если честно, то последующие патчи улучшили ситуацию, но снижение скорости рендеринга кадров всё равно присутствовало (и до сих пор есть). К 2019 году появились некоторые другие игры, поддерживающие этот API и выполняющие трассировку лучей для отдельных частей кадра. Мы тестировали Metro Exodus и Shadow of the Tomb Raider, столкнувшись с той же ситуацией — при активном использовании DXR заметно снижает частоту кадров.
Примерно в то же время UL Benchmarks объявила о создании теста функций DXR для 3DMark:

DXR используется в графической карте Nvidia Titan X (Pascal) — да, в результате получается 8 fps
Однако исследование игр с поддержкой DXR и теста 3DMark показало, что трассировка лучей даже в 2019 году по-прежнему остаётся очень сложной задачей для графического процессора, даже по цене в 1000 с лишним долларов. Значит ли это, что у нас нет реальных альтернатив растеризации?
Прогрессивные функции в потребительских технологиях 3D-графики часто оказываются очень дорогими, а их изначальная поддержка новых возможностей API бывает довольно фрагментарной или медленной (как мы это выяснили при дестировании Max Payne 3 на разных версиях Direct3D в 2012 году). Последняя проблема обычно возникает, потому что разработчики игр пытаются включить в свои продукты как можно больше современных функций, иногда не имея для этого достаточного опыта.
Однако вершинные и пиксельные шейдеры, тесселяция, HDR-рендеринг и screen space ambient occlusion тоже когда-то были затратными техниками, подходящими только для мощных GPU, а теперь они являются стандартом для игр и поддерживаются множество графических карт. То же самое станет и с трассировкой лучей; со временем она просто превратится в ещё один параметр детализации, включенный по умолчанию у большинства игроков.
В заключение
Итак, мы подошли к концу второй части анализа, в котором глубже рассмотрели мир 3D-графики. Мы узнали, как вершины миров и моделей переносятся из трёх измерений и превращаются в плоскую 2D-картинку. Мы увидели, что нужно учитывать область видимости и поняли, какое влияние она оказывает. Мы исследовали процесс преобразования этих верин в пиксели, а закончили кратким рассмотрением альтернатив традиционного процесса растеризации.
Как и в прошлой статье, мы вряд ли смогли раскрыть все темы, и пропустили отдельные детали — в конце концов, это же не учебник! Но мы надеемся, что вы узнали что-то новое и теперь уважаете труд программистов и инженеров, использовавших вычисления и науку для реализации всего этого в ваших любимых 3D-играх.
Автор: PatientZero






