Размерность Минковского и Two Nearest Neighbours (TwoNN)

В этой статье я кратко изложу абстрактную идею того, что такое внутренняя размерность геометрической фигуры, попутно введя один из вариантов размерности Минковского, а затем расскажу про другой, приблизительный способ оценки внутренней размерности, который применим к реальным (то есть, конечным) облакам точек и называется Two Nearest Neighbours (TwoNN). В конце статьи для интересующихся будут оставлены ссылки на несколько научных статей, в которых второй способ используется для анализов эмбеддингов нейросетей.

Итак, давайте разбираться!

Размерность Минковского

Допустим, у нас есть геометрическая фигура - например, круг. Как определить его размерность? Вопрос может показаться тривиальным - ведь минимальная размерность пространства, в которое можно вложить круг - два (плоскость - это двумерное пространство). Значит, размерность круга тоже два. Однако, такое наивное определение размерности геометрической фигуры (по минимальной размерности объемлющего пространства - в данном случае, двумерного) обладает очевидным недостатком: оно меняется даже при небольших деформациях нашей фигуры. Например, мы можем вложить круг в трехмерное пространство и слегка согнуть его - так, чтобы он перестал быть плоским. Тогда по нашему определению его размерность станет равна 3, что показывает большую ограниченность и условность такого наивного определения. Поэтому давайте рассмотрим другой, более тонкий способ оценить размерность фигуры, описанный в замечательном видео от 3blue1brown про фракталы (Рис. 1-3 ниже я тоже взяла оттуда).

Для этого мы поместим наш круг радиуса x на "клетчатую бумагу" с квадратиками со стороной a (пока что будем снова считать круг идеально плоским в целях упрощения изложения). А потом посчитаем, каким минимальным количеством квадратиков можно полностью его покрыть. Это количество, очевидно, будет зависеть от x и a, в данном примере оно равно 69:

Далее, если радиус x увеличить, то количество квадратиков, покрывающих круг тоже увеличится - например, при увеличении радиуса в два раза оно увеличивается до 234:

Пробуя разные радиусы x, можно увидеть, по какой именно закономерности растет минимальное количество квадратиков, покрывающих круг. Можно установить, что это количество, которое мы обозначим f(x), растет квадратично, то есть, пропорционально квадрату радиуса круга:

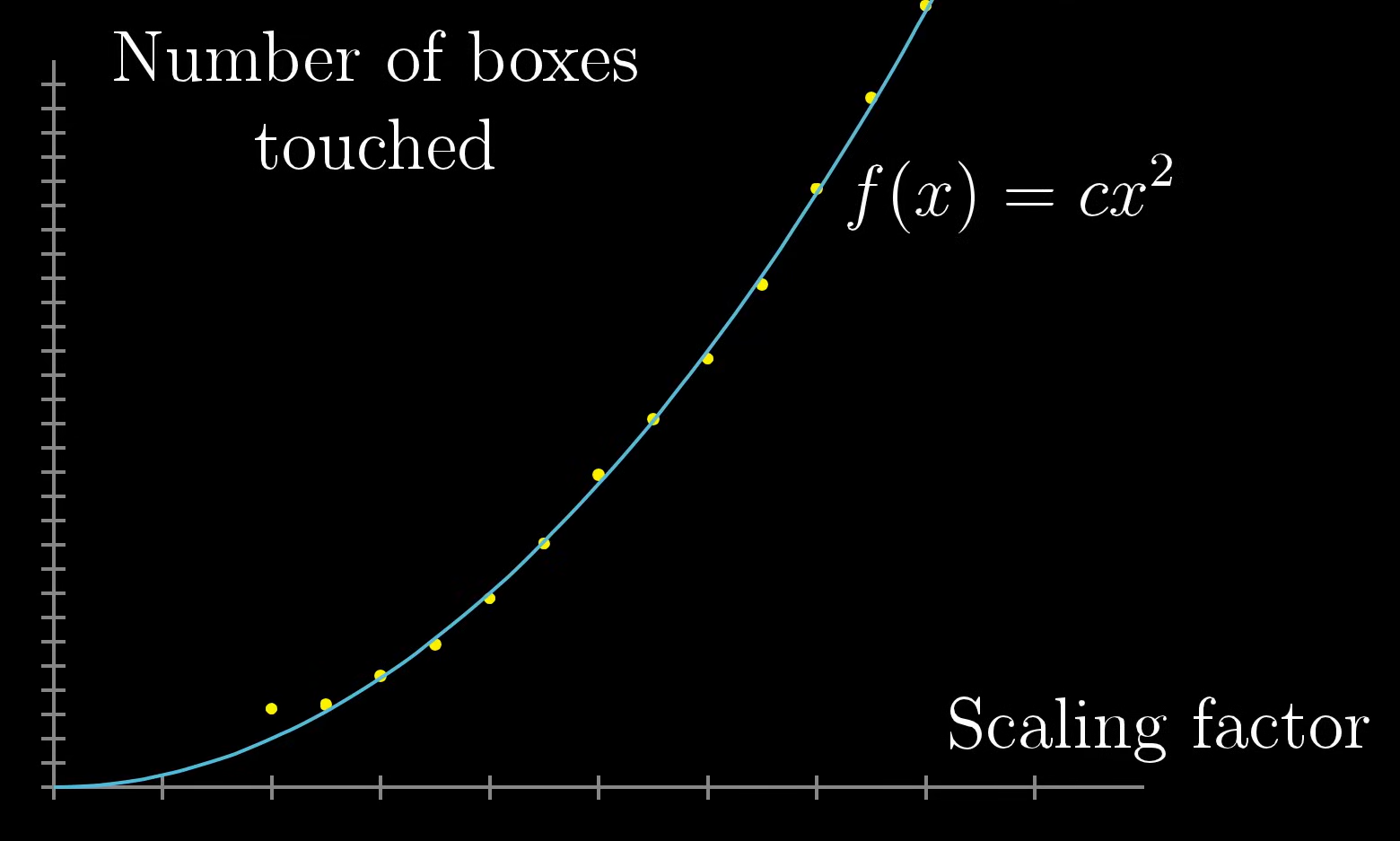
Примечание. конечно, те из читателей, что помнят школьную геометрию, уже догадались, что коэффициент c на картинке выше равен числу пи, а количество квадратиков, покрывающих круг, при x >> a приблизительно равно его площади; но мы не будем на этом останавливаться.

Что ещё интересно, если мы поместим тот же круг не на клетчатую плоскость, а в трехмерное пространство с трехмерной решеткой и будем считать не количество покрывающих его квадратиков, а количество покрывающих его кубиков, в пределе мы снова придем к такой же формуле. То есть, количество покрывающих его кубиков в пределе будет по-прежнему пропорционально квадрату его радиуса. При чем это будет верно даже для искривленного (в разумных пределах) круга. Можно показать, что то же самое будет происходить и в четырехмерном пространстве, и в пространствах более высокой размерности. То есть эта закономерность является некоторой неотъемлемой характеристикой круга, вне зависимости от того, куда его вкладывают и как искривляют.

С другой стороны, если вместо круга рассмотреть объемный шар, то количество покрывающих его кубиков в пространстве будет расти пропорционально третьей степени радиуса этого шара. Для читателей с хорошим пространственным воображением (или знанием того, что такое внешняя мера Жордана) это должно быть очевидно. Ну, а остальные могут сделать при желании численный эксперимент! 🤓

Таким образом, показатель степени в формуле на рис. 3 (напомню, формула выражает количество квадратиков/кубиков/многомерных кубиков, покрывающих ту фигуру, размерность которой мы хотим измерить), вполне неплохо совпадает с нашим интуитивным пониманием размерности.

Но что будет, если мы попробуем таким же образом исследовать не круг или шар, а нечто более сложное, например, треугольник Серпинского (рис. 4-5)?

Оказывается, в этом случае количество квадратов растет быстрее, чем по линейной закономерности, но медленнее, чем по квадратичной. В результате мы получаем в нашей степенной формуле дробную степень, то есть, дробную размерность, равную

Этот результат можно доказать или проверить экспериментально; он показывает способ численно оценить интуитивно понятный факт того, что треугольник Серпинского, благодаря своей бесконечно сложной структуре, как бы более "объемен", то есть в большей степени заполняет плоскость, чем прямая или отрезок, все же не столь "объемен", как полностью заполненная плоскость или заполненный круг.

Итак, мы сейчас рассмотрели первое определение внутренней размерности геометрической фигуры. Она называется размерностью Минковского. Также конкретно для приведенного выше варианта определения размерности Минковского с квадратиками и кубиками, можно встретить название upper-box dimension или просто box-counting dimension.

Примечание. Если вы не до конца поняли идею, я рекомендую просмотреть оригинальное видео от 3blue1brown и только потом вернуться к данной статье; ну, а если все хорошо, то давайте двигаться дальше.

Теперь у читателя может возникнуть вопрос: а почему статья называется "Размерность Минковского и Two Nearest Neighbours", а не просто "Размерность Минковского"? Зачем нам вводить определения каких-то других внутренних размерностей? Дело в том, что размерность Минковского корректно определена только если наша геометрическая фигура содержит бесконечное число точек. Если же мы поместим фигуру, составленную из конечного числа точек, на клетчатую плоскость и начнем ее растягивать так же, как делали это с кругом, то мы увидим следующее. Начиная с какого-то момента, количество квадратиков, покрывающих нашу фигуру, прекратит увеличиваться и станет константой и перестанет увеличиваться, потому что каждая точка будет покрыта ровно одним квадратиком. А если это количество равно константе, то показатель степени в формуле на Рис. 3 равен нулю.

Таким образом, размерность Минковского любой фигуры, состоящей из конечного числа точек, тоже будет равна нулю. Но ведь все реальные данные, которые мы встречаем в Data Science, как раз и состоят из конечного числа точек, в отличие от абстрактных геометрических фигур вроде кругов или фракталов из примеров выше. Конечно, можно попробовать приспособить размерность Минковского под конечные множества, но на практике это выходит не очень хорошо и эффективно. Поэтому и пришлось разработать для оценки внутренней размерности таких множеств новые, приблизительные, методы. При этом каждый такой метод имеет свою область применимости, так как рассчитан на множества определенного размера и основан на определенных предположениях о распределении, из которого пришли точки множества.

Two Nearest Neighbours

Один из таких методов - Two Nearest Neighbours или, кратко, TwoNN.

Он приблизительно оценивает внутреннюю размерность конечного облака точек - такого, для которого можно за разумное время посчитать и сохранить в памяти попарные расстояния между всеми парами точек (за исключением, может быть, тех, которые эвристика посчитает совсем далекими друг от друга).

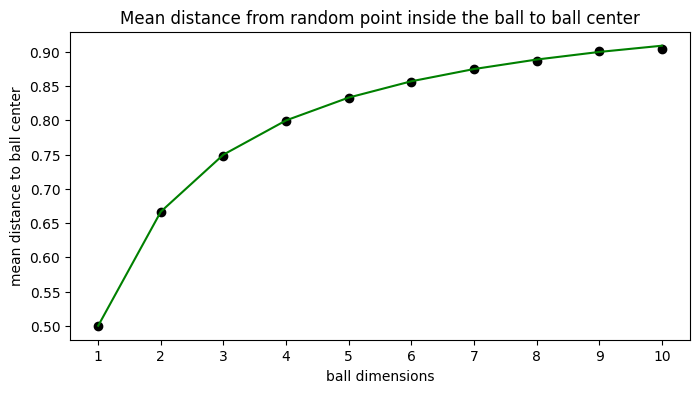
Метод основан на следующем математическом наблюдении. Возьмем n-мерный шар радиуса r и будем выбирать из него точки случайным образом, при этом считая, что все точки шара могут быть выбраны с равной вероятностью. Другими словами, зададим на нашем шаре равномерное распределение. Затем подсчитаем среднее расстояние от выбранных точек до центра шара. Можно доказать, что по мере увеличения количества выбранных точек, это расстояние будет стремиться к своему мат.ожиданию, заданному формулой

Согласно этой формуле, чем больше размерность нашего шара, тем ближе к поверхности шара будет находиться точка, случайно выбранная внутри него. Я сделала маленький colab-ноутбук, демонстрирующий эту интересную закономерность с помощью эксперимента. Вот график среднего расстояния в зависимости от размерности шара из ноутбука (радиусы у всех шаров здесь равны единице):

Теперь можно перейти к тому, что делает метод TwoNN для оценки внутренней размерности облака точек. Для произвольной точки датасета (назовем ее точка A), он находит ее самого ближайшего соседа (точку B) и следующего ближайшего соседа (точку C). Предполагается, что на маленьких масштабах облако точек, полученных из естественных данных, должно быть распределено более-менее равномерно, и поэтому считается, что точка B сэмплирована из равномерного распределения внутри шара с центром A и радиусом |AC|:

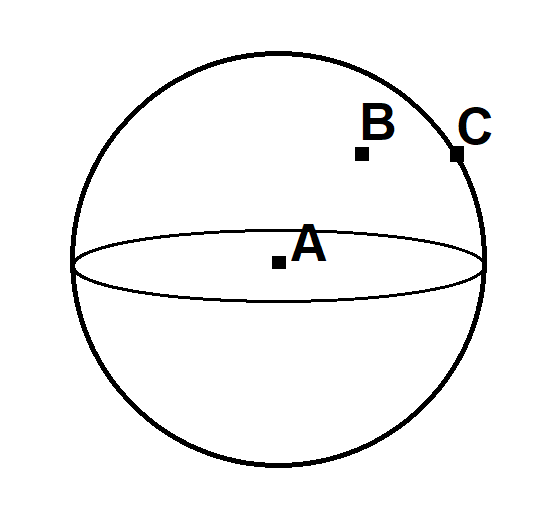
При этом размерность шара неизвестна - мы ведь можем в пространство большой размерности поместить и двумерный круг, и трехмерный шар, и сколько-угодно-мерный шар, если только его размерность не превышает размерность объемлющего пространства. Поэтому делается такой трюк: размерность шара n, из которого мы, по нашему предположению, сэмплировали точку B, выясняется из соотношения величин |AC| и |AB| (здесь и далее предполагаем, что |AB| строго меньше |AC| и для простоты не рассматриваем случай их равенства). Подставляя их вместо r и E(dist) в формулу выше, получаем:

Таким образом для каждой точки из нашего облака получатся некоторая очень-очень грубая оценка n. Кажется, что эта оценка взята с потолка; однако, если точек много, и мы посчитаем такую оценку для каждой из них, то случайности сгладятся, и по совокупному результату можно получить определенное представление о внутренней размерности всего облака точек как целого.

Конечно, оценка эта получается чаще всего дробной. Что, в принципе, не страшно, учитывая, что и размерность Минковского тоже бывает дробной. Однако, что хуже, эта оценка не всегда остается стабильной при увеличении количества точек в облаке, даже если они сэмплируются из одних и тех же реальных данных.

Объясняется это тем, что ключевое предположение о "равномерности" облака точек на малых масштабах - из которого, напомню, мы вывели нашу оценку на n, - в реальности выполняется в лучшем случае приблизительно. И чем дальше реальное распределение от этого предположения, тем хуже метод работает. Поэтому всегда нужно проверять, насколько оценка стабильна при изменении размера датасета, если она сильно меняется, это значит, что предположение о равномерности генерирующего распределения на малых масштабах было неверным. Более подробно про теоретическое обоснование и ограничения метода TwoNN написано в статье на Nature Scientific Reports под названием Estimating the intrinsic dimension of datasets by a minimal neighborhood information.

Two Nearest Neighbours реализован в библиотеке skdim и является одним из инструментов, который используется для анализа эмбеддингов нейросетей и встречается в различных научных статьях, например:

• Intrinsic dimension of data representations in deep neural networks

• Intrinsic Dimension, Persistent Homology and Generalization in Neural Networks

• The Shape of Learning: Anisotropy and Intrinsic Dimensions in Transformer-Based Models

В этих статьях установлены некоторые закономерности относительно того, как различается внутренняя размерность TwoNN на эмбеддингах хорошо обученных и плохо обученных сетей, а также как она распределена по слоям сети.

К сожалению, пока что я не видела более прикладных применений TwoNN. Если вы их знаете, поделитесь в комментариях! Также дайте знать, если заметили какую-либо неточность в изложении и вообще расскажите о своих впечатлениях. А я в следующий раз постараюсь рассказать вам о двух других способах, более сложных, но и более стабильных способах на практике оценки внутренней размерности - PHD (Persistent Homology Dimension) и MLE (Maximum Likelihood Estimation).