
Недавно мой один знакомый подарил мне старую SD карту памяти фирмы «Canon» на 128 МБ, которую нашёл где-то на улице. Её вполне мог кто-нибудь просто выкинуть, так как обычному пользователю ей очень сложно найти применение в современных технических условиях. Объём 128 МБ по нынешним временам считается очень малым, да и в смартфон её не вставишь ввиду больших габаритов. В основном распространены карты памяти microSD, которые вставляются в большинство смартфонов, но были также ещё и miniSD. Карты памяти малого объёма (MMC 8 МБ, 16 МБ) я встречал лет 20 назад в miniDV видеокамерах. Они там использовалась в качестве дополнительного носителя для сохранения фотографий.
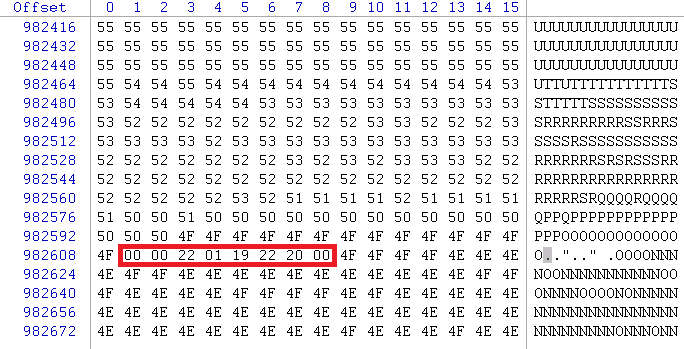
Мне не столько была нужна эта карта памяти, сколько было интересно, что на ней записано. Она была испорченная, так как при её вставке в компьютер она не определялась. Точнее говоря, раздел файловой системы на ней отсутствовал, или файловая система была битая. При попытке открыть диск система предлагала отформатировать карту памяти. Я не спешил это делать, напротив, решил на всякий случай сделать её резервную копию в дисковом редакторе. Как потом оказалось, это я сделал не зря. Фрагмент начала дампа карты памяти в HEX редакторе представлен на рисунке ниже.

До этого я по-быстрому попробовал применить программы по поиску и восстановлению удалённых разделов, программы по восстановлению удалённых файлов популярных форматов, – безуспешно. Такое ощущение, что карта памяти никогда не использовалась или была полностью очищена. Пролистав дамп карты памяти до конца, я увидел, что она действительно практически пустая, и искать на ней что-либо вообще нечего. На самых первых секторах есть какие-то значимые байты, но потом в основном идут байты FF (пустота). Их я выкинул из образа, оставив только значимые байты. Среди значимых байтов я не увидел ни одного слова в их текстовой интерпретации ASCII: нету заголовков каких-либо дисковых разделов или файловой системы. В глаза бросаются длинные цепочки одинаковых байтов. Также заметно, что байты в смежных цепочках отличаются на единицу. Мне стало очень интересно, что бы это обозначало? Что это за информация? Случайна она, или эти байты что-то значат? Всматриваясь в эти цепочки более внимательно, я увидел, что иногда эти цепочки обрываются, и между ними вставляется цепочка из 8 разных байтов, среди которых последний и первые два – нулевые (рис. 3). Иногда встречаются точно такие же последовательности, но их предваряет цепочка из нескольких байтов значением 0xFF.
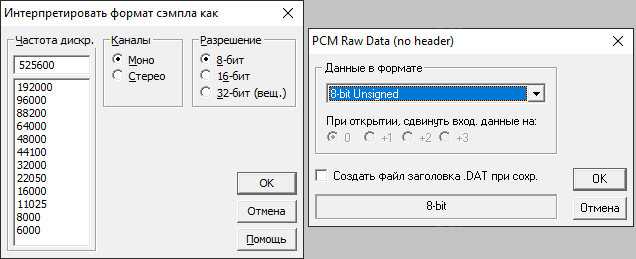
Я решил открыть образ карты памяти в моём любимом Adobe Audition, как беззнаковые PCM-данные формата «8 бит, Моно» с любой частотой дискретизации для графической визуализации байтов. Похожую процедуру, которая на первый взгляд кажется бессмысленной, я уже проделывал, о чём не раз писал в предыдущих статьях. После успешного открытия я увидел очень интересную картину, в которой залип надолго.
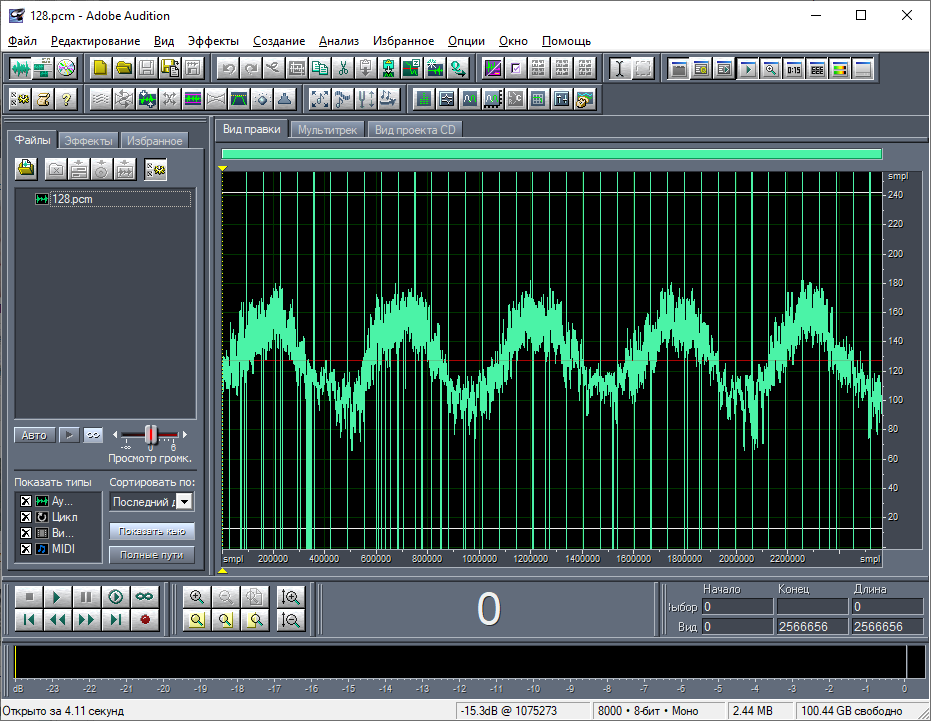
Самое первое, что бросается в глаза – 5 периодов синусоидальных колебаний, смешанных с шумом, и куча равномерно отстоящих вертикальных полосок. Также можно заметить присутствие других вертикальных полосок в нижней части волны. При увеличении масштаба волны сразу стало видно, что 5 периодов колебаний смешаны не с шумом, а с более высокочастотными колебаниями (хотя слабый шум также виден) (рис. 5). А вертикальные полоски, разумеется, – это короткие отрезки данных, в составе которых есть байты с очень малыми и очень большими значениями (рис. 6). В частности, большие значения равны 0xFF. Можно сделать предварительный вывод, что данные на карте памяти представляют собой последовательность чисел, описывающий какой-то периодический процесс, снабжённые какими-то заголовками. Есть и неравномерно отстоящие друг от друга полоски, которые чуть меньше по высоте. Это заголовки другого вида, которые не предваряются байтами 0xFF. Их присутствует гораздо меньше.
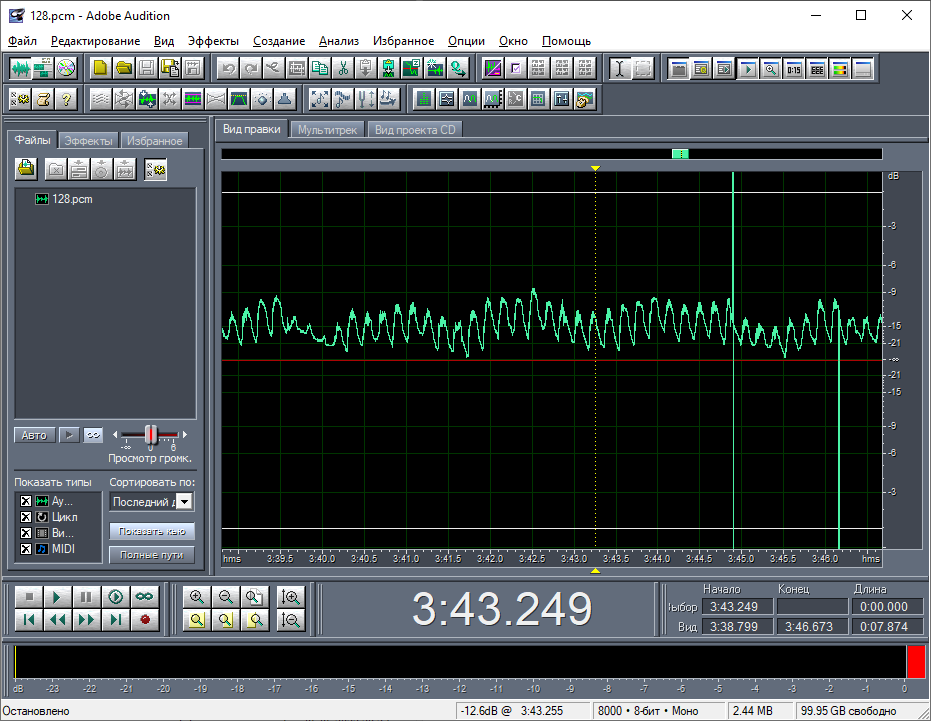
Частотный спектр данных не особо впечатляет (рис. 7). При этом, разумеется, не важно, какую частоту дискретизации я указываю на этапе открытия файла. Это влияет только на частотную линейку, определяя как бы масштаб частот. Как видно из рисунка, основное частотное пространство занимает шум, а спектры всех описанных выше колебаний прячутся в самом низу. То есть, частота дискретизации сильно и неоправданно завышена.
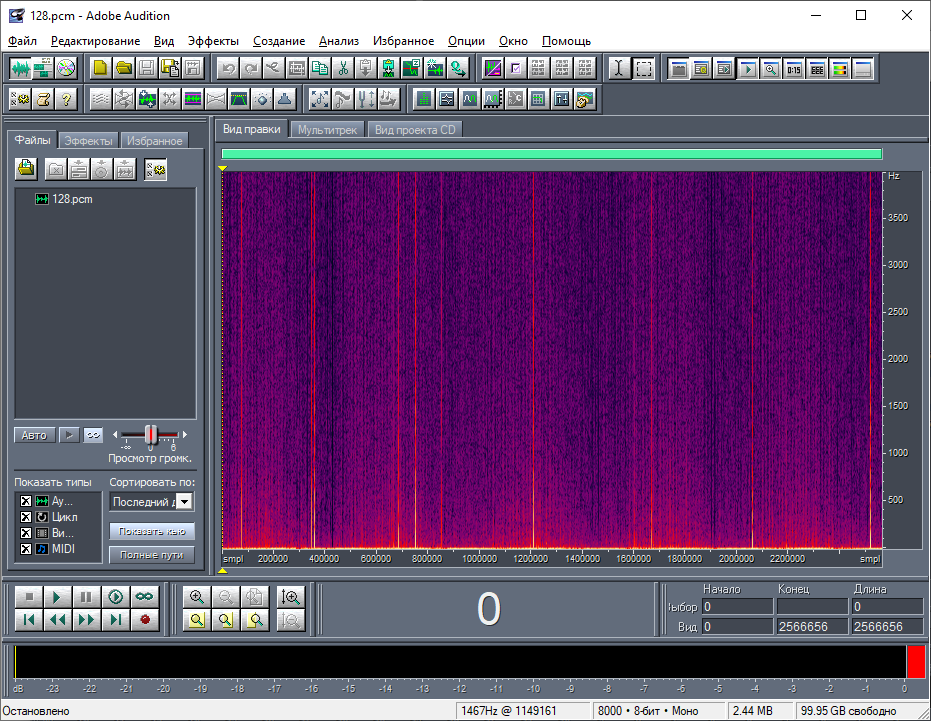
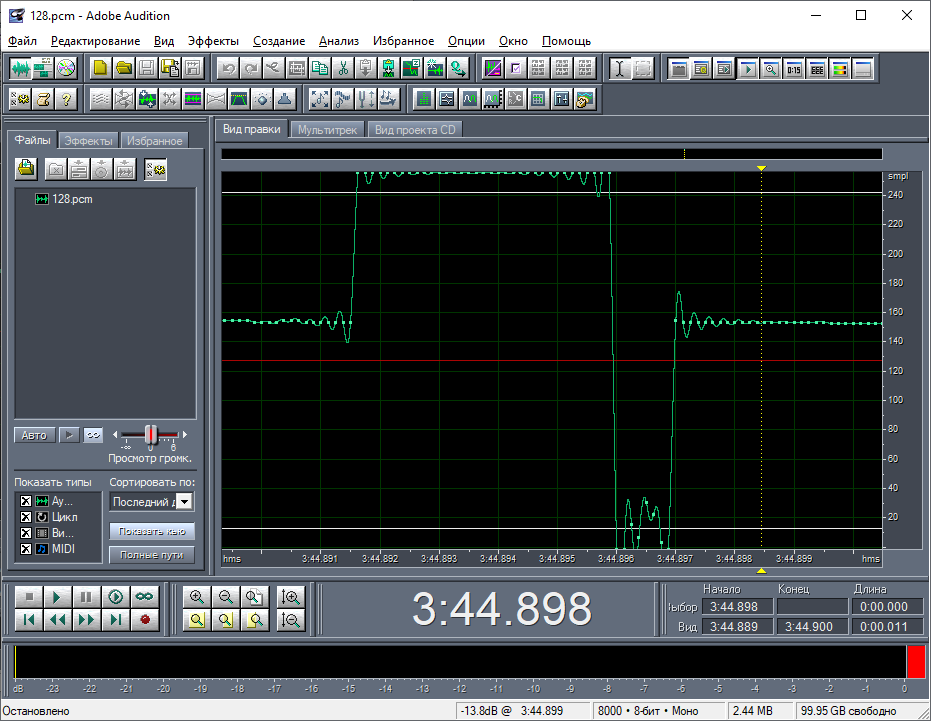
Я решил выполнить даунсэмплинг 100:1, открыв данные с заранее большой частотой дискретизации в 800000 Гц. После этой процедуры вертикальные полоски, которые относились к заголовку, практически замаскировались в сигнале (рис. 8). Очевидно, это произошло, потому что их длина не превосходит 100 байт. Максимум, что от них осталось, это один сэмпл. При этом высокочастотные колебания не пострадали, то есть, не вышли за пределы частоты дискретизации (рис. 9). Это дало возможность посмотреть спектральный состав в более наглядной форме (рис. 10).
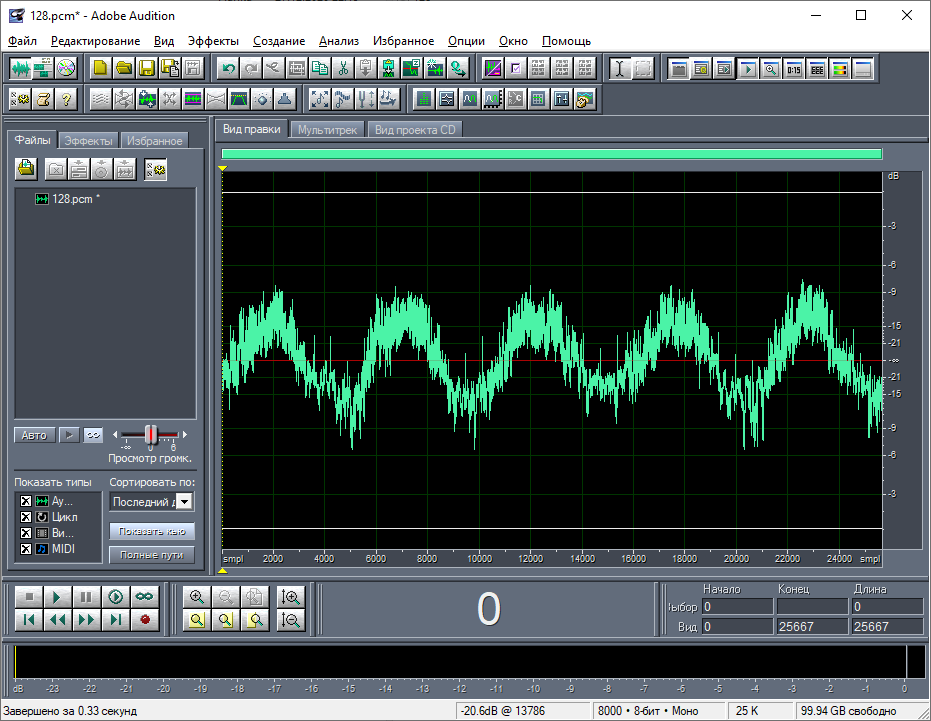
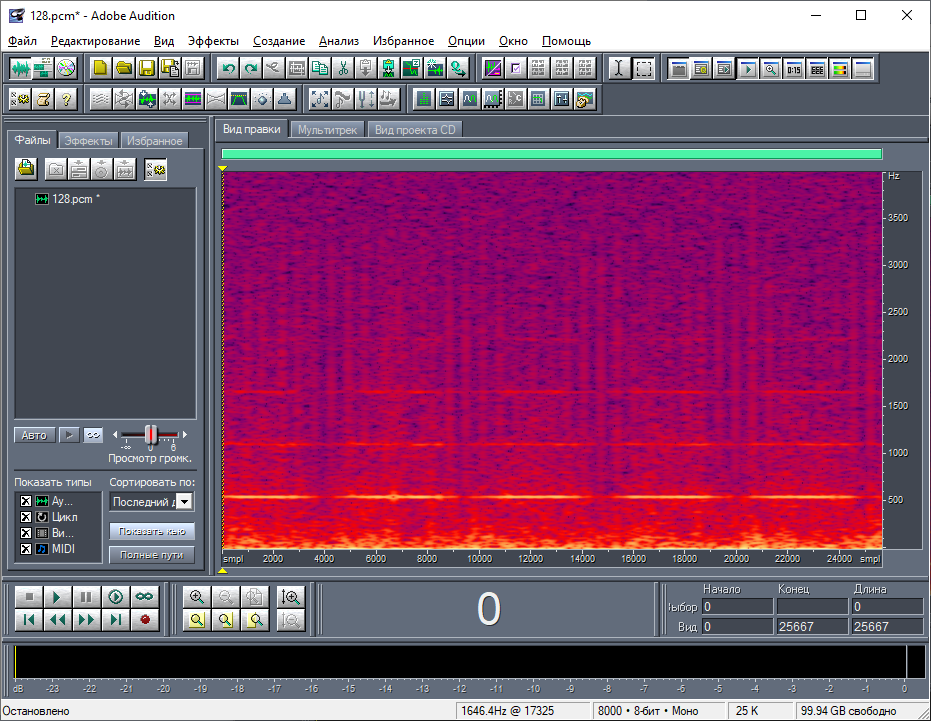
Кроме шума на спектре присутствует основная частота (около 500 Гц), выраженная самой яркой линией, а также наблюдаются её верхние гармоники, выраженные гораздо слабее. На волновом виде их заметить практически нереально. Линии основной частоты и её гармоник не являются сплошными. Они плавно «гаснут» в пяти местах, которые соответствуют малым значениям сэмплов самых низкочастотных колебаний. То есть, грубо говоря, чем больше значения НЧ колебаний, там больше амплитуда ВЧ колебаний, которые к ним подмешены. Сразу пока мне непонятно, что это за процесс, который описывает этот сигнал. И почему он в таком виде записан на карту памяти? Однако я больше чем уверен, что это цифровые данные какого-то сигнала, собранные через какие-то равные промежутки времени.
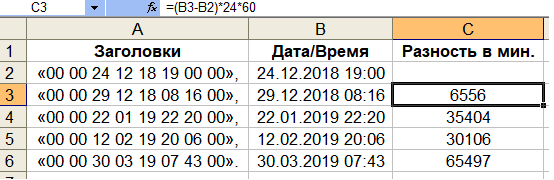
Для изучения и анализа содержимого я написал короткую программу, которая выполняет две вещи. Во-первых, вырезает из моего образа заголовки, формируя целиковый файл PCM данных без заголовков (рис. 11, вертикальные полоски отсутствуют). Во-вторых, переписывает байты заголовков в отдельный файл. То есть, программа разделяет байты данных и байты заголовков на два файла. Заголовки распознаются по следующему правилу. Данное правило я предварительно сформулировал на основе анализа заголовков при просмотре образа в HEX редакторе. Заголовок состоит из 8 байтов. Первые два байта и последний байт являются нулевыми. Заголовок может предварять несколько байтов со значением 0xFF, но их нужно игнорировать. Вот для примера выписка пяти идущих друг за другом заголовков из произвольно взятого места:
«00 00 24 12 18 19 00 00»,
«00 00 29 12 18 08 16 00»,
«00 00 22 01 19 22 20 00»,
«00 00 12 02 19 20 06 00»,
«00 00 30 03 19 07 43 00».
У меня были догадки, что это какие-то метки времени, а может быть это индексы блоков. Я начал анализировать байты заголовков. Не считая нулевые байты, третий байт от заголовка к заголовку меняется как-то случайно. Значение четвёртого байта склонно к тенденции возрастания, но не превосходит 0x12. Значение пятого байта возрастает гораздо реже. Сначала оно равно 0x17, затем – 0x18, и в итоге в конце образа доходит до значения 0x21. Значения шестого и седьмого байта случайны (или псевдослучайны). Стоит обратить внимание, что шестнадцатеричные числа в последовательности «0x17, 0x18, 0x19, 0x20, 0x21» (пятые байты заголовка) не являются смежными, как кажется это на первый взгляд! После числа 0x19 пропущены числа 0x1A, 0x1B,…, 0x1F, которые бы довели последовательность до монотонно возрастающей. И я считаю, что это сделано не просто так. Это похоже на двоично-десятичный код, когда цифры исходного десятичного числа кодируются 4-мя битами (полубайтами). В такой кодировке десятичные числа в шестнадцатеричном представлении отображаются «без потерь», то есть в исходном десятичном виде. На этом этапе я вспомнил про микросхемы часов реального времени (RTC), с которыми приходилось неоднократно работать. Внутри них дата и время представляется как раз в двоично-десятичной кодировке. И если взглянуть внимательнее на пример заголовков выше, учитывая вышеописанное поведение байтов, можно придти к предварительному выводу, что заголовки обозначают дату и время. Третий, четвёртый и пятый байты – число, месяц и год соответственно. Шестой и седьмой байты – часы и минуты. Тем более, как я позже проанализировал, шестой байт никогда не превосходит 0x23, а седьмой – 0x59.
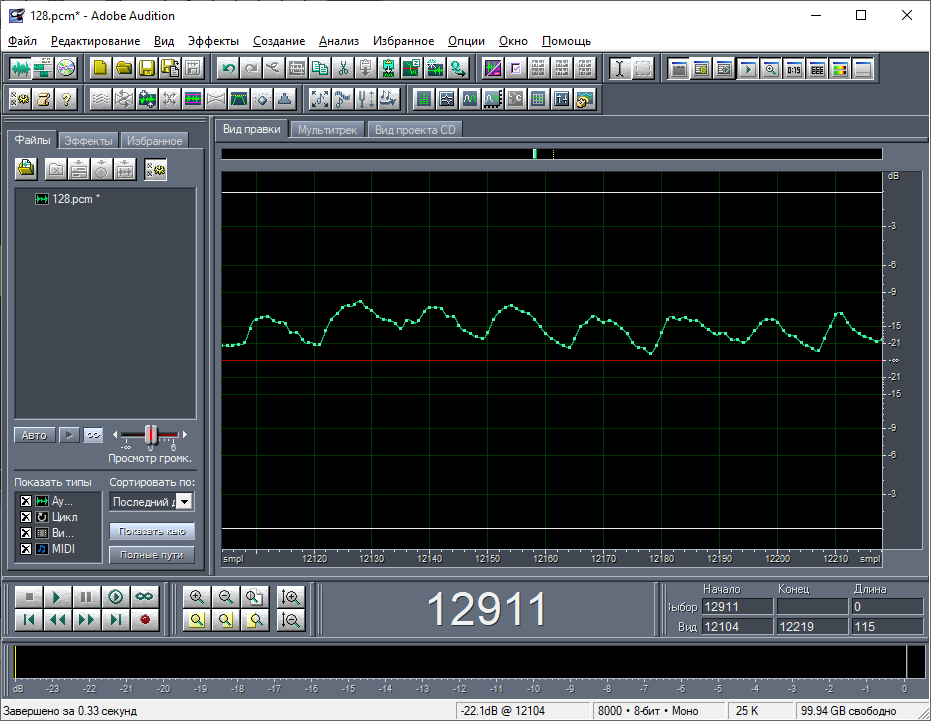
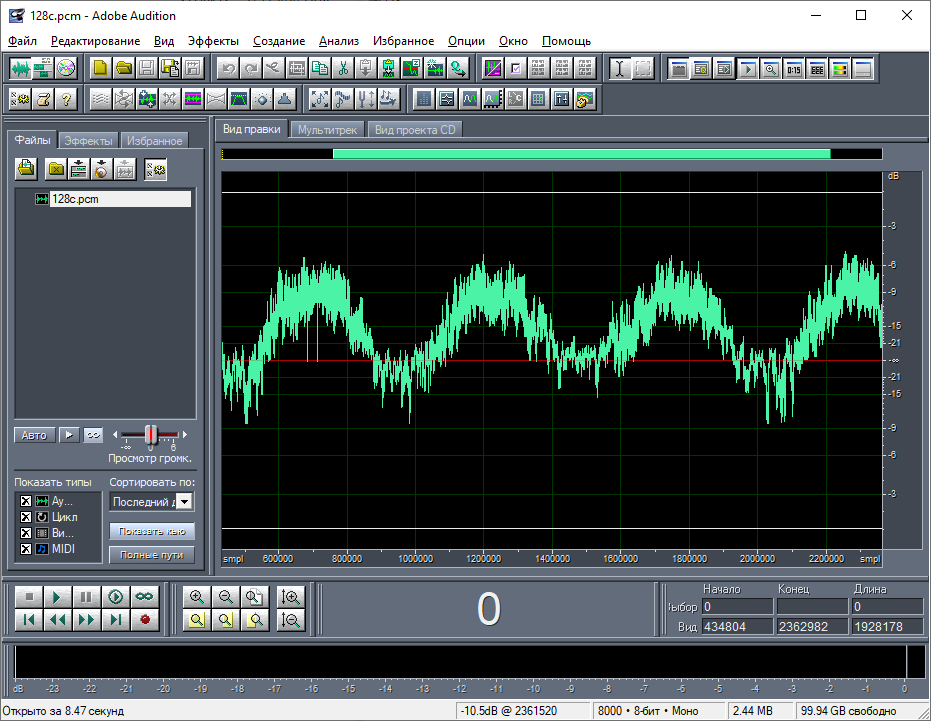
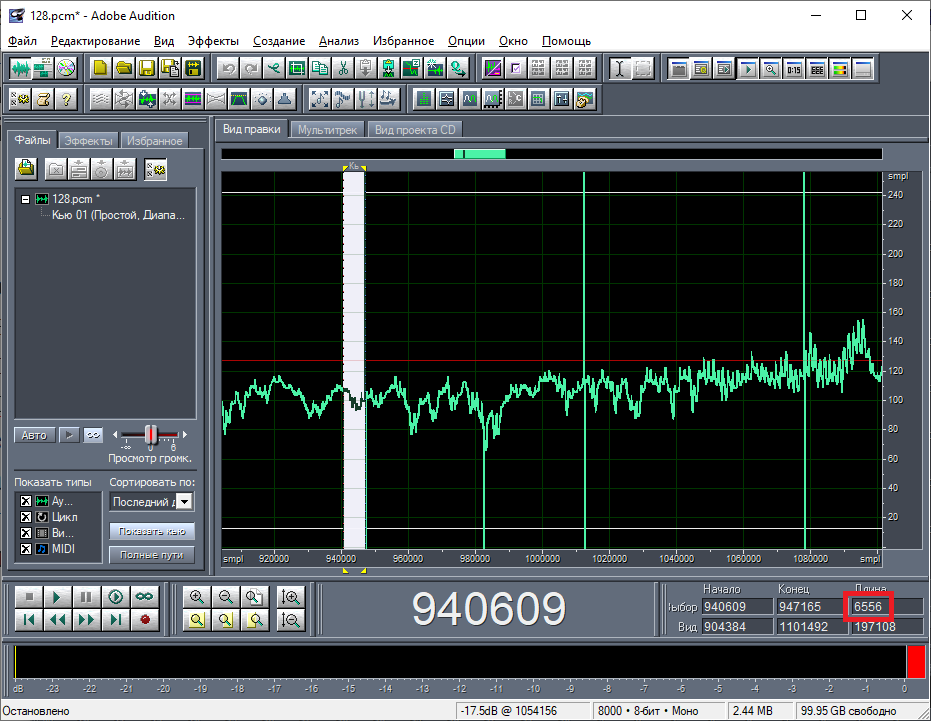
В Adobe Audition на волновом виде по значениям смещений я нашёл именно те заголовки, которые показаны в примере (рис. 12). В программе Excel я посчитал разности во времени между соседними заголовками (рис. 13). Так как дата и время в заголовках указана с точностью до минуты, то логично разность считать в минутах. Значения разностей получились неодинаковые. Длина содержимого между соседними заголовками, как можно заметить в Adobe Audition, прямо пропорциональна значению разности даты и времени между этими заголовками. Я выделил содержимое между первым и вторым заголовком (из примера). Длина этого промежутка составляет 6556 сэмплов (байт) (рис. 14). Как оказалось, это значение в точности совпадает со значением разности даты и времени между этими заголовками, выраженным в количествах минут. Я проверил данную закономерность на других примерах – везде всё сходится. Стало быть, байты данных соответствуют минутам, а заголовок даёт привязку начала фрагмента данных к абсолютному начальному времени.

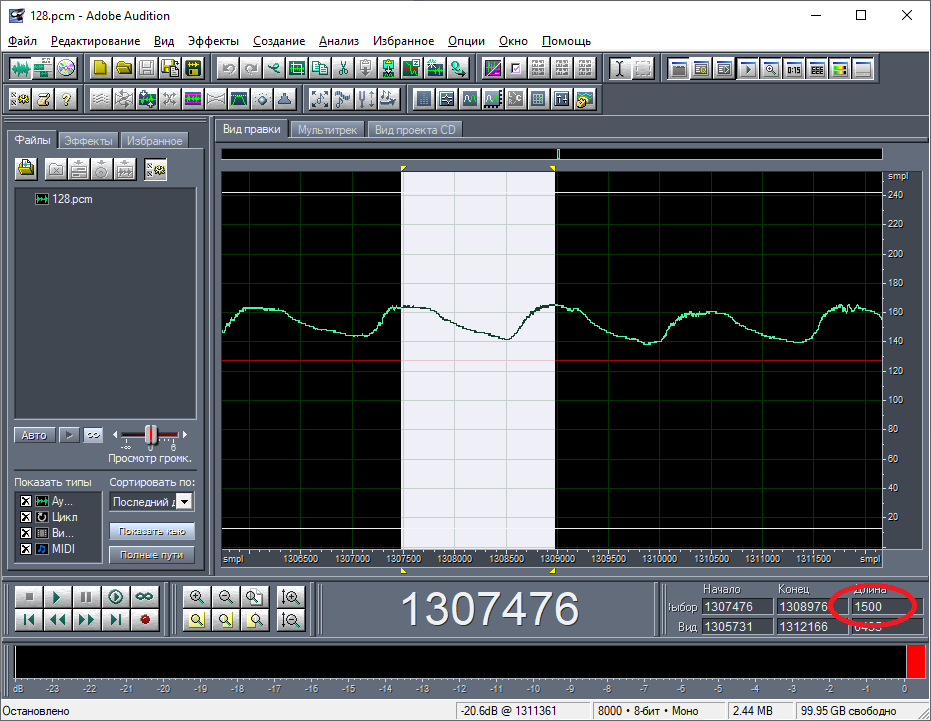
Теперь осталось определиться, что представляют собой эти данные. По моей оценке длина периода высокочастотных колебаний составляет приблизительно 1500 сэмплов (рис. 15). Но с очень большой вероятностью более точное значение периода – 1440. Это нечто иное, как число минут в сутках (60*24), то есть, период высокочастотных колебаний во временном представлении составляет 1 сутки.
Период низкочастотных колебаний, предположительно, составляет 1 год. До этого я уже оценивал, что частота ВЧ колебаний примерно в 350 раз выше частоты НЧ колебаний. Принимая во внимание все вышеизложенные факты, можно сделать вывод, что цифровые данные представляют собой поминутную запись какого-то процесса, в котором присутствуют суточные и сезонные колебания. А если учесть привязку к времени и дате, то при детальном анализе видно, что минимальные значения НЧ колебаний приходятся на зимние месяцы года, а максимальные – на летние. Для ВЧ колебаний максимальные значения приходятся на дневные часы, а минимальные – на ночные. Я предполагаю, что это запись измерения температуры воздуха (но это не точно).
Больше всего меня смущает тот факт, что значения байтов беззнаковые. Я пробовал открывать образ карты памяти в Adobe Audition как PCM данные знакового типа, но при такой конфигурации, судя по графику на волновом виде, не сохраняется монотонность, что было бы вовсе непрактично (рис. 16). Поэтому байты данных имеют беззнаковый тип.
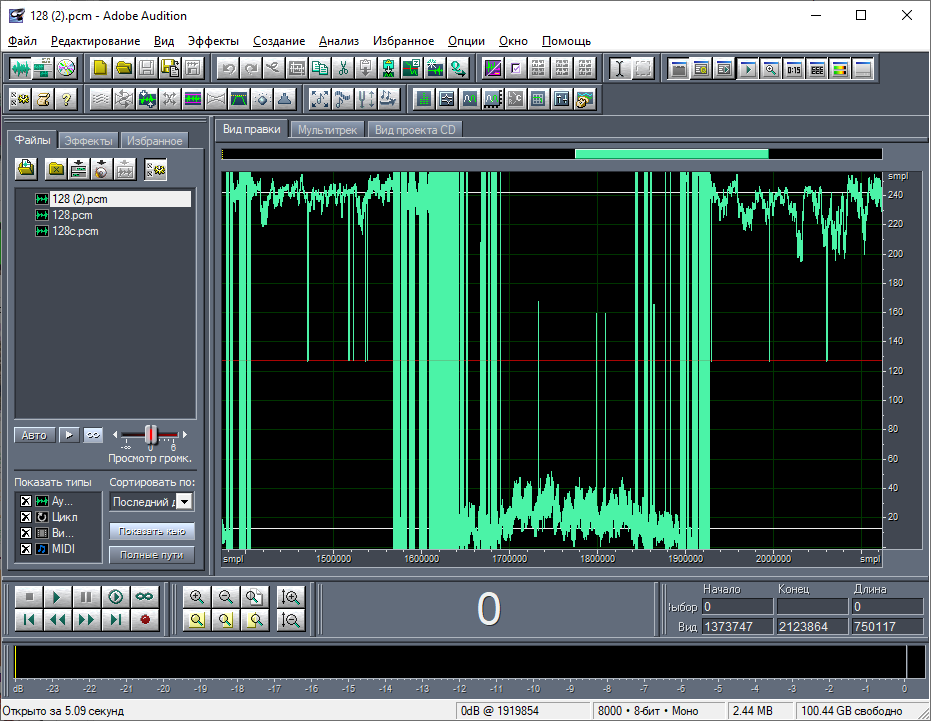
Осталось определить, какова зависимость значений температуры в градусах от значений байтов. Предположительно зависимость линейная. Должен быть коэффициент масштаба и значение смещения. Думаю, что значение смещения нулевое и данные центрированы относительно линии тишины Adobe Audition. Стоит помнить, что значение байтов для линии тишины соответствует не 0, а 127, так как это беззнаковый тип данных. Что касается масштабирования значений температур, то здесь очень сложно сделать какие-либо предположения. Диапазон значений исследуемых данных, как видно из волнового вида, составляет примерно от 80 до 200 (от -47 до 73, если пересчитать относительно линии тишины) (рис. 17). И если при этом принять во внимание масштаб 1:1 (1 единица на градус), то получается, что данные отображают процесс изменения температуры от -47 до 73 градусов. На температуру воздуха это не похоже. Если прикинуть масштаб 1:2, то получается диапазон примерно от -24 до 36 градусов. А это уже ближе к практической истине! На этом я, пожалуй, и остановлюсь.
Таким образом, на карте памяти записаны измерения температур в виде RAW данных, начиная с 1-ого сектора. RAW данные форматированы определённым образом: имеются заголовки, в которых содержатся временные метки для привязки измерений к дате и времени. Температура «оцифрована» в течение 5 лет с точностью до полградуса, и измерения сделаны раз в минуту.
В заключение я напишу о нескольких интересных операций по работе с этими цифровыми данными. Как я писал выше, я указывал заранее большую частоту дискретизации 800000 Гц, затем делал даунсэмплинг до 8000 Гц, т.е. в 100 раз. Эти значения я выбрал наугад. Но можно подобрать такое значение частоты дискретизации, при котором Adobe Audition отобразит цифровые данные с более удобным масштабом времени. Например, 1 сек. шкалы времени Adobe Audition на 1 год записи температурных данных. Коэффициент масштабирования при этом составит 3600*24*365.25=31557600. Столько секунд в году. Но так как один сэмпл соответствует одной минуте (60 секундам) записи, а одну секунду я хочу привести к одному году, то из этого следует, что PCM данные нужно открыть с частотой дискретизации 31557600/60=525960 (рис. 18). Столько минут в году и столько же сэмплов в одной секунде. Открывать я буду чистый файл, т.е. очищенный от заголовков.
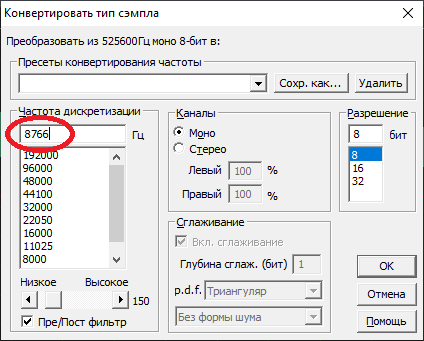
Картина никак не поменяется, будет видно всё тоже, как и раньше. Из-за слишком большой частоты дискретизации (по сравнению со скоростью изменения данных), как я уже писал, полезные составляющие спектра прячутся в самом низу. Чтобы их увидеть, нужно выполнить даунсэмплинг. При исследовании я понижал частоту дискретизации в 100 раз. Это число я брал также наобум. Но можно взять и более разумное число того же порядка, например, 60. То есть, нужно конвертировать частоту дискретизации до 525960/60=8766 Гц (рис. 19). Почему именно 60? В этом есть смысл. Полученные после даунсэмплинга цифровые данные будут обозначать не поминутную температуру, а почасовую. То есть, один сэмпл будет соответствовать одному часу, а температурные данные будут приблизительно усреднены за каждый час. При этом период суточных ВЧ колебаний будет составлять 24 сэмпла (рис. 20).
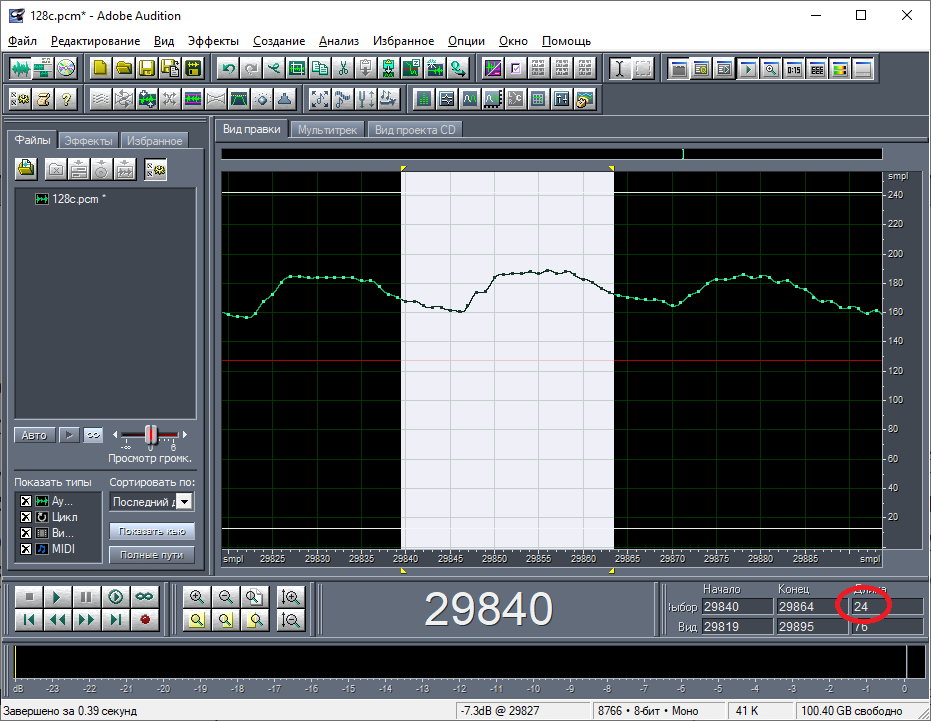
Спектральный состав останется практически тем же, как и на рис. 10 (рис. 21). На нём не будет следов от остатков заголовков, и он будет чуть шире по частотному диапазону. Также немного скорректируется частотный масштаб.
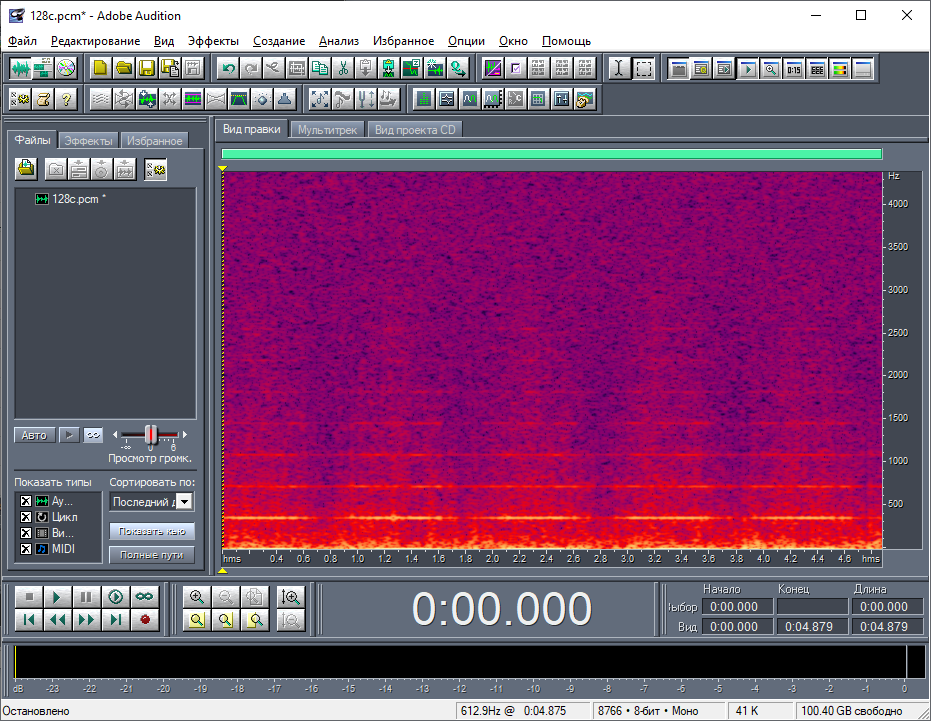
На рис. 10 частота ВЧ колебаний составляла примерно 500 Гц, а в новом преобразованном сигнале данная частота будет равняться 365.25 Гц. Объяснить это довольно просто. Если НЧ колебания, соответствующие году, приведены к одной секунде, то их частота, очевидно, равна 1 Гц. А частота суточных ВЧ колебаний в 365.25 раз больше (число суток в году). Более того, эти PCM данные можно воспроизвести, как звук. У меня на частоте дискретизации 8766 Гц проблем с воспроизведением не было. Но лучше выполнить преобразование на ближайшую стандартную частоту дискретизации 8000 Гц. Масштаб частот при этом не поменяется, уменьшится только частотный диапазон. Но он и так получился с запасом: всё, что выше 2000 Гц, – шум. Аудиозапись длится столько секунд, сколько лет производилась запись температуры. То есть, она как бы ускорена в 31557600 раз. В моём случае она длится 4.8 сек.
Меня до сих пор волнует вопрос о происхождении гармоник суточных колебаний в составе сигнала. Это частоты 2f, 3f, 4f, …, где f=365.25 Гц. Будто бы, кроме основных колебаний суточных периодов, есть слабовыраженные колебания с периодами 12ч., 8ч., 6ч. и т.д. Вряд ли они обусловлены особенностями записи и преобразований. Скорее всего, это объясняется особенностью самой природы. Но не следует забывать о том, что источник этих данных неизвестен! То, что это температуры, это моё личное предположение, основанное на описанных выше анализах и личном опыте.
Автор: Артём






