Алгоритмы поиска пути — неотъемлемая часть разработки игр. А также различных систем навигации, ориентации и много чего ещё. Но мы сосредоточимся на именно игровой индустрии и алгоритмах, которые в ней применяются.
Каждый игровой разработчик сталкивается с задачей, в которой требуется заставить персонажа(или бота) пройти из одной точки в другую, при этом не собрав все стены. А разработчикам стратегий ещё нужно учитывать проходимость клеток(дороги, болота, леса и так далее). Вот здесь на помощь приходят алгоритмы поиска пути.

Зачем?
Из вышесказанного можно сделать вывод, что любому игровому разработчику рано или поздно приходится сталкиваться и разбираться с поиском пути, а позже и модифицировать и оптимизировать его для собственных проектов. А так как очень много новичков сразу идут в GameDev для них не всегда просто прочитать несколько статей и понять тот или иной алгоритм. В этом посте описаны попытки создать программное обеспечение, которое поможет облегчить процесс понимания принципов работы алгоритмов поиска пути.
Несколько слов об основных алгоритмах
Мы будем рассматривать 3 основных алгоритма. Теперь в двух словах о каждом из основных алгоритмов и скриншоты визуализации их работы в программе (немного опережая события).
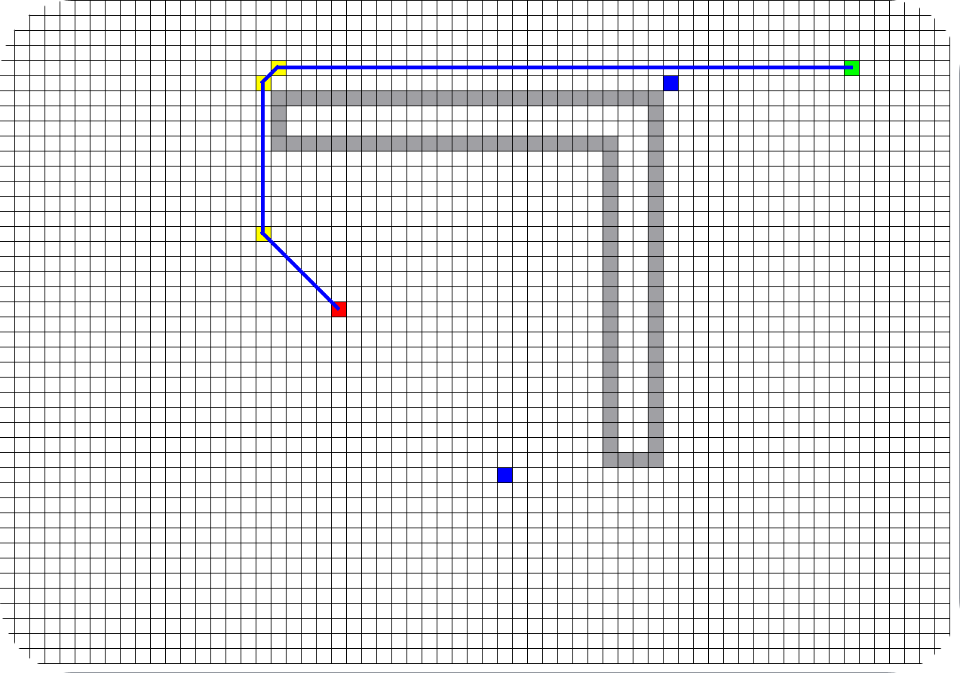
Алгоритм Дейкстры
Разработан нидерландским учёным Эдсгером Дейкстрой в 1959 году. Алгоритм проверит каждую из вершин графа пока не найдет кратчайший путь до исходной вершины. Подробнее можно прочитать, например, тут.
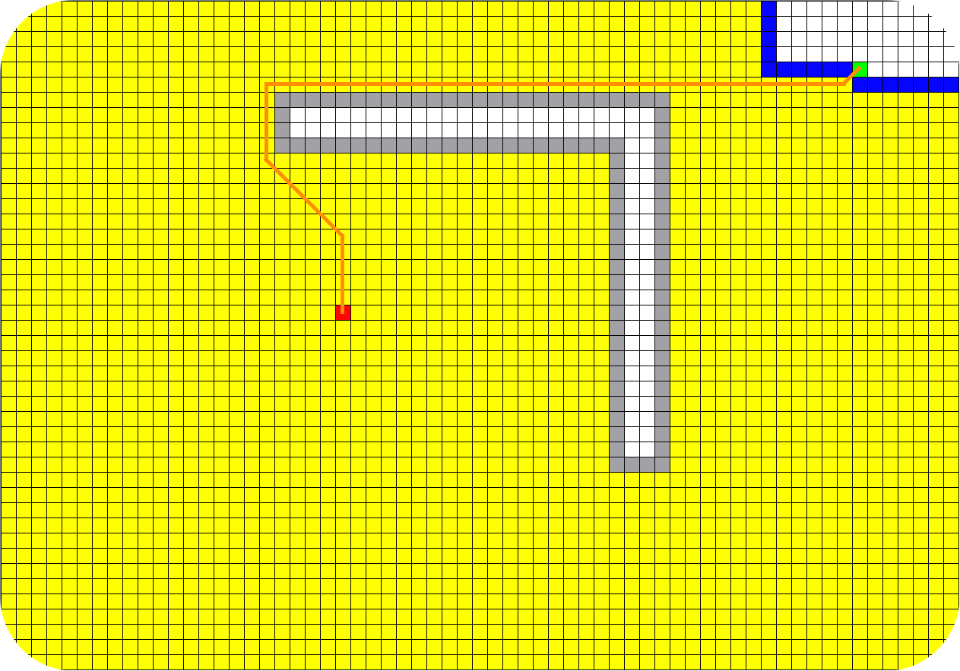
A*(A Star)
Этот алгоритм был впервые описан в 1968 году Питером Хартом, Нильсом Нильсоном и Бертрамом Рафаэлем. При рассмотрении каждой отдельной вершины переход делается в ту соседнюю вершину, предположительный путь из которой до искомой вершины самый короткий.
Начать изучение можно здесь.
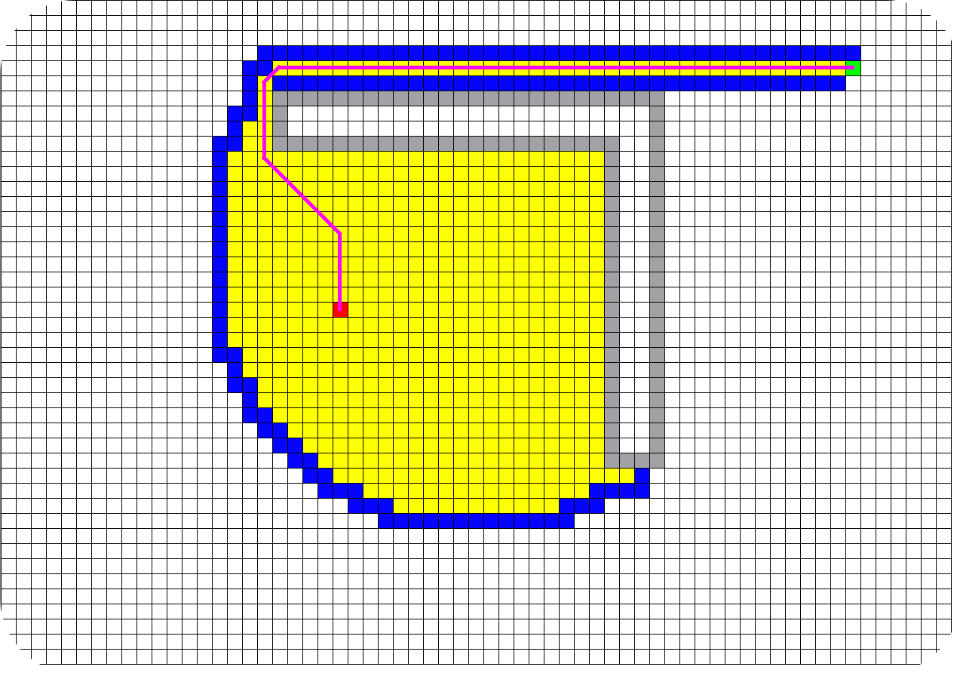
Jump Point Search
Данный алгоритм был представлен в 2011 году Д. Харбором и А. Грастиеном. JPS ускоряет поиск пути, «перепрыгивая» многие места, которые должны быть просмотрены. «Прыжковые точки» позволяют ускорить алгоритм поиска пути, рассматривая только «необходимые» узлы. Очень хорошо объясняется принцип работы здесь
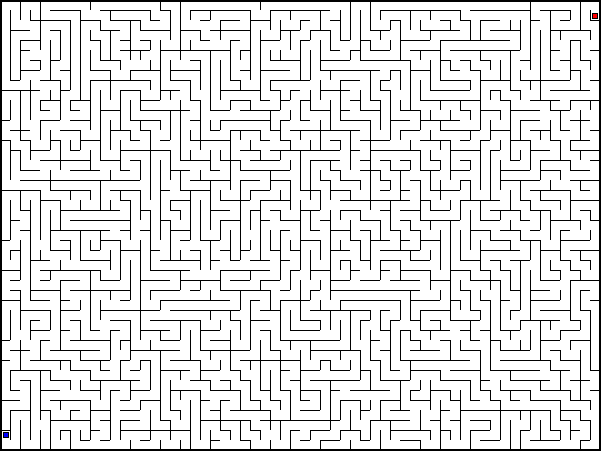
Небольшая оговорка
Стоить отметить, что Growing Tree генератор, также представленный в программе, создает «классический лабиринт» как на картинке ниже(только больше), высота и ширина в настройках далее задается именно для него. Этот генератор был добавлен для создания «Вау-эффекта» у новичка и для демонстрации пути, построенного самыми базовыми алгоритмами(Правило правой или левой руки, DFS), в посте я не буду здесь останавливаться и сосредоточусь на ручном режиме.
Основа поиска — клетчатое поле
Поиск работает на графе, самый простой создать из карты граф — это расставить вэйпоинты самому перевести карту в клетчатое поле. Так как цель — облегчить понимание основ, мы и собираемся работать с квадратными клетками.
Для начала нам стоит определить класс клетки. У пользователя должна быть возможность установить вход, выход и нанести на поле непроходимые препятствия, также для изучения полезно узнавать характеристики клетки, её родителя и статус прямо во время работы алгоритма. В итоге получаем представленный класс (set-, get-функции я убрал для экономии места):
enum Status{ Click, Unclick, Enter, Exit, NoStatus };
enum ListStatus {NoList, InClosed, InOpen};
class GraphicsCell : public QGraphicsRectItem
{
public:
GraphicsCell(int, int, int, bool *, bool *, bool *, QGraphicsItem *parent = 0);
void pressButton(int buttonID);
void showInfo(QPoint pos);
void updateStatus(int upd);
void deleteInfo();
private:
int x;
int y;
int f;
int g;
int h;
int weight = INT_MAX;
Status status;
ListStatus listStatus;
bool *isEnter;
bool *isExit;
bool visited;
GraphicsCell *par;
QGraphicsRectItem *infoBox;
};
Функции pressButton и updateStatus обрабатывают изменение статуса и цвета клетки. А showInfo и deleteInfo за инфобокс, о котором далее. Переменные x и y отвечают за координаты; f, g, h, weight за характеристики необходимые для работы алгоритмов поиска, status и listStatus за
статус клетки, isEnter и isExit за то, существует ли на карте вход и выход, par за родительскую клетку(необходимо для восстановления построенного пути).
Работа с полем
Клетчатое поле мы создали, теперь хорошо бы предоставить пользователю возможность наносить вход и выход, расставлять стены и вызывать вышеупомянутый инфобокс.
К счастью, класс QGraphicsView из фреймворка Qt, на котором мы и создаем интерфейс, предоставляет нам виртуальные функции щелчка, двойного клика и движения курсора (mousePressEvent, doubleClickEvent, mouseMoveEvent соответственно). Их мы и перегружаем в классе сцены, которая содержит наши клетки.
Функция checkPos проверяет, чтобы курсор находился над объектом клетки.
void MazeWindow::mousePressEvent(QMouseEvent *event)
{
checkPos(event);
GraphicsCell *currCell = static_cast<GraphicsCell *>(scene()->itemAt(mapFromGlobal(cursor().pos()), QTransform()));
if (currCell == NULL)
return;
if (startStatus == Status::NoStatus)
{
if (currCell->status == Status::Click)
startStatus = Status::Click;
else
startStatus = Status::Unclick;
}
if (event->button() == Qt::RightButton)
{
currCell->showInfo(mapFromGlobal(cursor().pos()));
cellWithInfo = currCell;
}
else
currCell->pressButton(event->button());
}Реализация функции щелчка. Определяем по какой клетке мы нажали и просим её обновить свой статус. Инфобокс пришлось поставить на ПКМ, так как в Qt при использовании двойного клика сначала вызывается функция обычного клика и это приводило к мерцанию клетки(мы обновляли состояние клетки при одинарном клике и возвращали его назад, когда понимали, что клик двойной).
Вход ставится на 'Ctrl + ЛКМ', а выход на колесико мыши или для тачпада 'Alt + ЛКМ'. Достаточно удобно. Стена устанавливается обычным ЛКМ.
void MazeWindow::mouseMoveEvent(QMouseEvent *event)
{
checkPos(event);
GraphicsCell *currCell = static_cast<GraphicsCell *>(scene()->itemAt(mapFromGlobal(cursor().pos()), QTransform()));
if (currCell == NULL)
return;
if (cellWithInfo != NULL && currCell != cellWithInfo)
{
cellWithInfo->deleteInfo();
cellWithInfo = NULL;
}
if (currCell->status == Status::Enter || currCell->status == Status::Exit)
return;
if (event->buttons() & Qt::LeftButton)
{
if (startStatus == Status::Click && currCell->status == Status::Click)
currCell->updateStatus(1);
else if (startStatus == Status::Unclick && currCell->status == Status::Unclick)
currCell->updateStatus(0);
}
}Также хотелось позволить пользователю рисовать стены, как это сделано в привычных графических редакторах, зажав ЛКМ, водить по полю.
Для этого перегружаем функцию mouseMoveEvent(). Проверяем, чтобы мы были над клетками, и просим обновить состояние клетки под курсором. Если начать рисовать с пустой клетки, то и продолжим рисовать стены, если стерли стену, то и далее будем в режиме «ластика». Функция ещё отвечает за удаление инфобокса, если мы убираем курсор с клетки, на которой он был вызван.
Инфобокс создадим как обычный прямоугольник, на котором показаны характеристики веса, F, G, H (если вы знакомы с представленными выше алгоритмами, то знаете эти обозначения), текущий статус клетки и её родитель.

Всё, мы обеспечили работу поля для визуализации, половина сложной работы сделана, ура!
Визуализация хода работ по поиску пути
Самая интересная часть программы, то, что должно превращать скучную (или не очень) статью в нечто такое:

Есть и пошаговый режим, который, в связке с инфобоксами, поможет на 100% понять работу каждого алгоритма.
Теперь пару слов о том, как это реализовывалось. Для примера рассмотрим функцию алгоритма AStar, остальные алгоритмы реализованы аналогично. Также мы оставим передачу сигнала от кнопки к самой функции.
bool MazeWindow::ASolve(int mode)
{
currMode = 0;
if (a == NULL)
{
//Удаление предыдущего решения, если оно существует
if (aL != NULL)
scene()->removeItem(aL);
clearLabyr();
a = new A(&labyr);
a->solveMaze(0);
}
if (mode == 0)
{
while (!a->solveMaze(1));
//Отображение
updatePictureSolve(Algorithms::AStarAlgo);
currMode = 1;
return true;
}
else
{
if (a->solveMaze(1))
{
//Отображение
updatePictureSolve(Algorithms::AStarAlgo);
QMessageBox msgBox;
msgBox.setText(tr("Sucsess"));
msgBox.setIcon(QMessageBox::Information);
msgBox.exec();
currMode = 1;
return true;
}
}
return false;
}Пошаговый режим и полное решение мы реализовывали одной функцией, поэтому приходится передавать ID режима(0 — полное решение и 1 — для очередного шага). Далее, если это полное решение или первый шаг в пошаговом, очищаем поле от остатков предыдущего решения, чистим статусы клеток и обновляем характеристики c помощью функции clearLabyr. Функции самих алгоритмов реализованы так, что возвращают истину, если достигнута конечная точка поиска или поиск продолжать невозможно, и false, если можно работать дальше. Следовательно, для полного решения оператором while вызываем функцию, пока она не вернет true и наносим на сцену линию пути вызвав функцию updatePictureSolve. Для пошагового режима вызываем функцию при каждом щелчке, если путь найден, также отправляем его на отрисовку и выводим сообщение, чтобы пользователь случайно не прокликал момент решения.
Сами алгоритмы поиска обновляют статус клеток, когда заносят их в открытый или закрытый список.
Панель управления
В программе представлены:
- Два типа генераторов: Growing Tree и ручной режим(клетчатое поле, о котором говорилось выше)
- Пять типов алгоритмов: DFS и поиск по правилу руки для Growing Tree генератора, а также Дейкстра, AStar, JPS для ручного режима.
Необходимо было позволить пользователю удобно переключаться между назваными опциями. Результатом великого дизайна работы стала небольшая панелька меню в рабочей области, которую можно скрыть и вызвать через тулбар. Есть возможность менять цвета линии пути, кликнув по цветному полю.(если вам не нравится мой вкус)
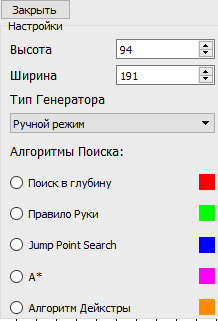
Работа со статистикой
Программой также можно воспользоваться, чтобы выбрать наиболее эффективный алгоритм для данной ситуации:
- Примерно рисуем необходимую карту, получается что-то как на картинке
- Запускаем все 3 алгоритма, на глаз оцениваем работу.
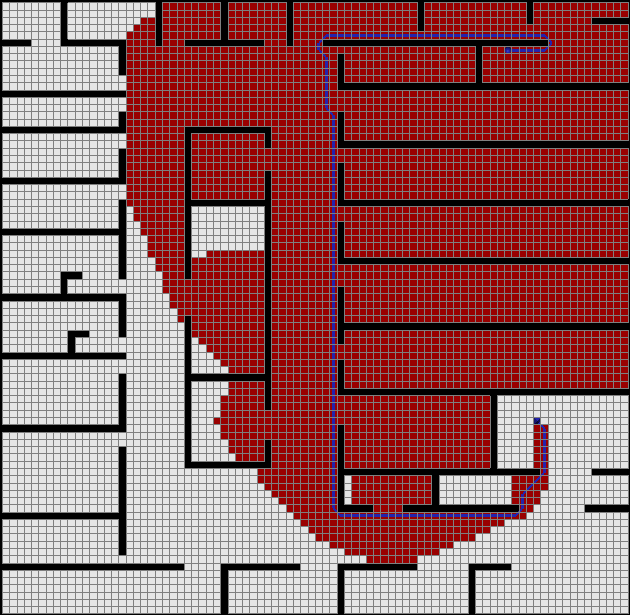
Очевидно, что для более менее серьёзных проектов «на глаз» недостаточно, поэтому необходимо отображать статистику.
Мы будем делать это в виде виджета с краткой статистикой текущего алгоритма в рабочей области и отдельного окна, отображающего работу всех алгоритмов за сеанс и позволяющего создать отчет, который можно будет скопировать, например, в Excel, построить там графики.
Реализация виджета с краткой статистикой очень походит на реализацию виджета с настройками, да и выглядит он почти также:
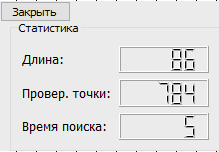
Алгоритм сам подсчитывает количество операций. Длину пути можно узнать из характеристик клетки выхода, а время мы считаем таймерами, вычитая время потраченное на рисовку(хотя это не очень то и точно). Когда алгоритм заканчивает работу он передает статистику на виджет и вызвает функцию создания записи в таблице. В итоге имеет такую таблицу:
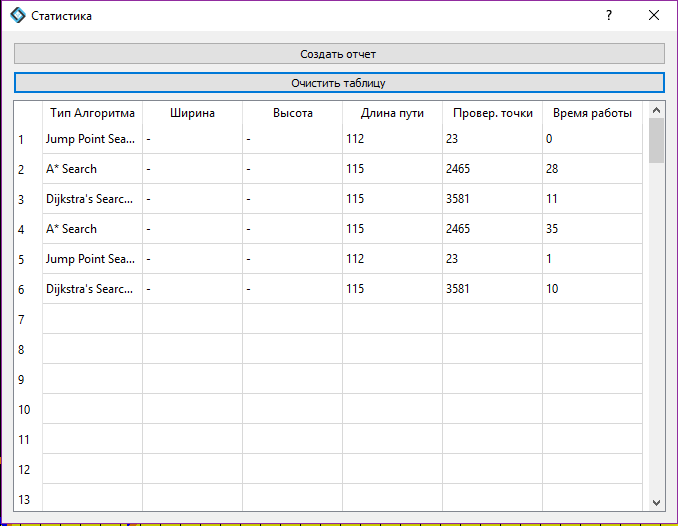

Такой график:
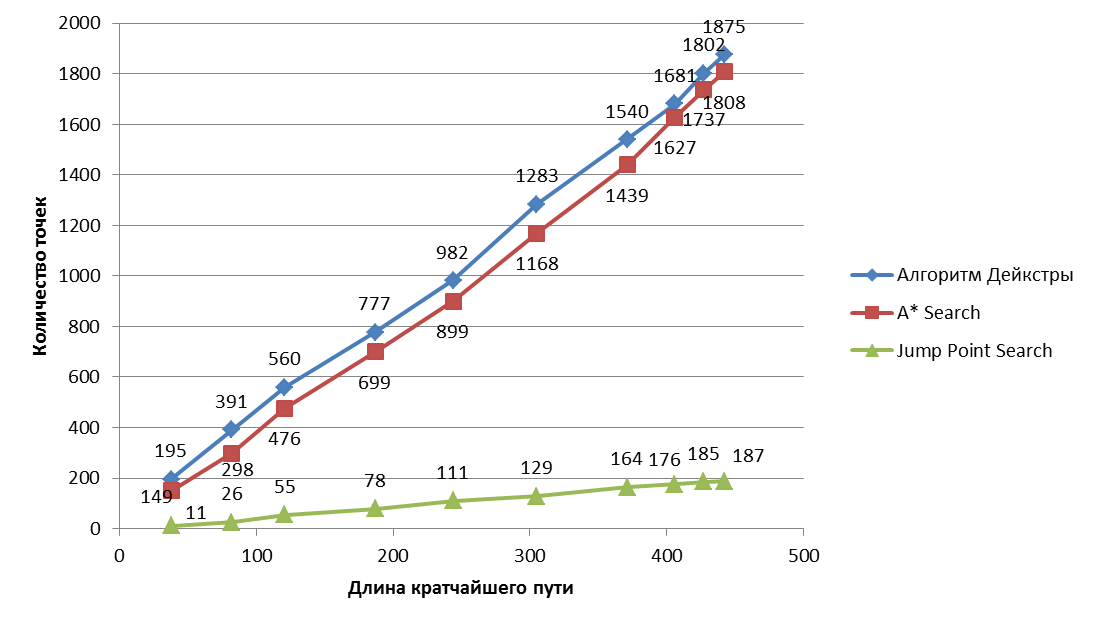
Заключение
Мы получили программу, которая помогает начинающим, и не только, программистам разобраться с алгоритмами поиска пути. По крайней мере я всё-таки помог паре своей друзей)
Автор будет рад выслушать ваши пожелания и исполнить их, как только напишет экзамены.
Возможно, череда улучшений приведет к тому, что мы получим мощную библиотеку с алгоритмами, а программа станет приятной демкой для неё (Как PathFinding.js, только лучше).
Если вы, возможно, хотели бы написать статью о поиске пути, можете приложить к ней и эту программу.

→ Скачать архив с программой можно с ЯД или с DropBox.
Автор: GDV_Fox






