Хочу поделиться опытом участия в конкурсе Kaggle и алгоритмами машинного обучения, с помощью которых добрался до 18-го места из 1604 в конкурсе Avazu по прогнозированию CTR (click-through rate) мобильной рекламы. В процессе работы попытался воссоздать оригинальный алгоритм «Мактрикснета», тестировал несколько вариантов логистической регрессии и работал с характеристиками. Обо всём этом ниже, плюс прикладываю полный код, чтобы можно было посмотреть, как всё работает.
Рассказ делю на следующие разделы:
1. Условия конкурса;
2. Создание новых характеристик;
3. Логистическая регрессия – прелести адаптивного градиента;
4. Матрикснет – воссоздание полного алгоритма;
5. Ускорение машинного обучения в Python.
1. Условия конкурса
Предоставленные данные:
- 40.4 млн записей для обучения (10 дней показов рекламы Avazu);
- 4.5 млн записей для тестирования (1 день).
Сами данные можно скачать здесь.
В качестве критерия оценки была заявлена отрицательная вероятность ошибки (Negative Likelihood Loss – NLL):
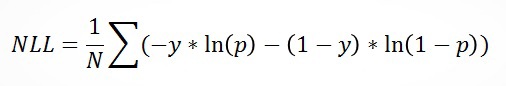
Где N – это кол-во записей, y – это значение переменной click, p – вероятность того, что событием был клик («1»).
Важным свойством этой функции ошибки является то, что если p основана на сигмоид функции, то частной производной (далее, градиентом) будет (p-y).
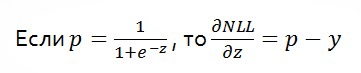
2. Создание новых характеристик
Для начала посмотрим на исходные данные, с чем мы можем работать:
- сlick – «0» – не было клика, «1» – был клик, это цель для предсказания;
- hour – время и дата показа рекламы;
- banner_pos – расположение баннера (предположительно, первый экран, второй и т.д.);
- site*, app* характеристики – информация о месте показа рекламы;
- device* характеристики – информация о девайсе, на котором показывается реклама;
- C1, C14-C21 — зашифрованные характеристики (предположительно, включающие в себя данные о геолокации показа, часовом поясе и, возможно, другую информацию).

Это не очень большое поле для работы, так как у нас нет исторических данных по пользователям, а самое главное — мы ничего не знаем о том, что за реклама показывается каждый раз. А это важная составляющая (вы ведь кликаете не на всю подряд рекламу?).
Что создаём нового:
- Полиноминальные характеристики 2-го уровня (3-й слишком замедляет процесс обучения);
- User_id. Тестировал несколько вариантов, лучше всего работает – device_id + device_ip + device_model + C14 (предположительно география на уровне города / региона). И да, device_id не равняется user_id;
- Частота контакта с рекламой. Обычно пользователи, которые видят рекламу в 100-й раз за день, реагируют на неё не так же, как те, кто видит в 1-й. Поэтому считаем частоту каждого показа для каждого user_id.
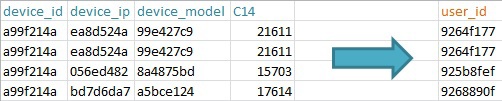
Идеи пробовал разные, указанные выше дали наилучший результат. При их формировании в основном основывался на своём опыте работы в рекламе и том, что можно было вытащить из данных Avazu.
Также делаем небольшие преобразования/трансформации данных, направленные, прежде всего, на избавление от повторяющейся информации:
- hour – выделяем час, выбрасываем день;
- C1 – предполагаю, что за этим скрывался часовой пояс, поэтому после 2 числа сливаю с колонкой час;
- С15 и C16 – объединяем, так как за ними легко угадывается ширина и высота баннера, нет смысла оставлять лишние характеристики;
- Site* и app* — трансформируем в placement*, так как понятно, что баннер показывается либо на сайте, либо в приложении, а остальные значения – это просто зашифрованный NULL, который доп. информации не несёт;
- Убираем все значения, которые не встречались в тестовых данных. Это помогает уменьшить переобучение.
Все изменения тестировал с помощью логистической регрессии: они либо давали улучшения, либо ускоряли алгоритм и не ухудшали результаты.
3. Логистическая регрессия (Logistic Regression) – прелести адаптивного градиента
Логистическая регрессия – популярный алгоритм для классификации. Есть 2 основные причины такой популярности:
1. Простота для понимания и создания алгоритма;

2. Скорость и адаптивность предсказания на больших данных за счёт стохастического градиентного спуска (stochastoc gradient descent, SGD).
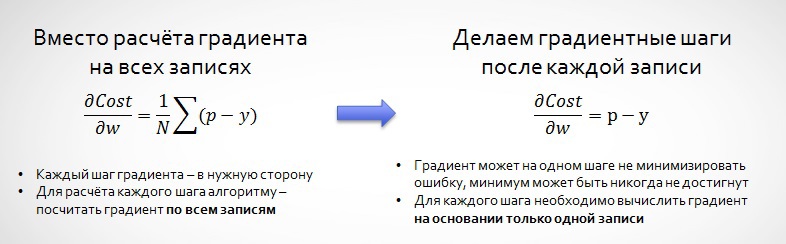
На примере данных Avazu посмотрим, как из-за стохастического градиента мы не всегда «идём» точно к минимуму:
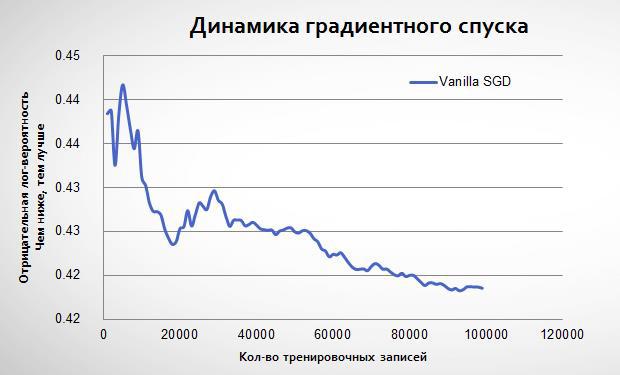
3.1. Адаптивный градиент
Однако если со временем сокращать скорость обучения алгоритма (learning rate), то мы будем приходить всё к более точному решению, так как градиент будет не так сильно реагировать на нетипичные данные. Авторы адаптивного градиента (Adaptive Gradient, AdaGrad) предлагают использовать сумму всех предыдущих градиентов, чтобы уменьшать последовательно скорости обучения:
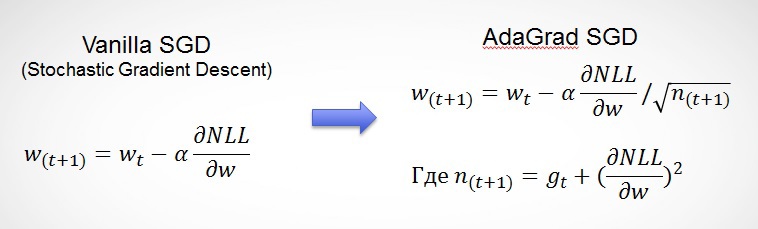
Таким образом, мы получаем полезные свойства алгоритма:
- Более гладкий спуск к минимуму (скорость обучения уменьшается со временем);
- Альфа для каждой характеристики рассчитывается индивидуально (что очень важно для sparse данных, где большинство характеристик встречаются очень редко);
- В расчете альфы учитывается, насколько сильно менялся параметр (w) характеристики: чем сильнее менялся раньше, тем меньше будет меняться в будущем.
Адаптивный градиент начинает обучаться так же, как обычная логистическая регрессия, но потом приходит к более низкому минимуму:
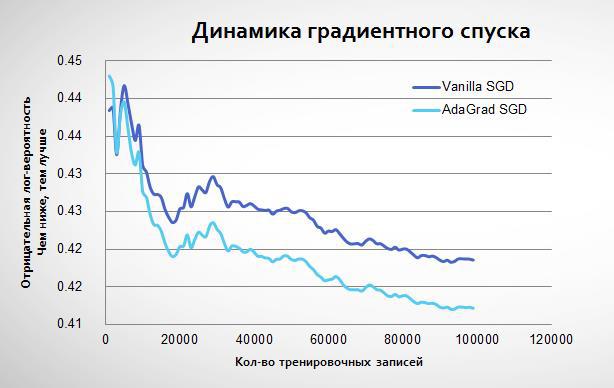
По факту если обычный стохастический градиентный спуск повторять много раз на одних и тех же данных, то он может приблизиться к AdaGrad. Однако это займёт больше итераций. В своей модели я использовал комбинацию этих техник: 5 итераций с обычным алгоритмом, а потом один с AdaGrad. Вот результаты:
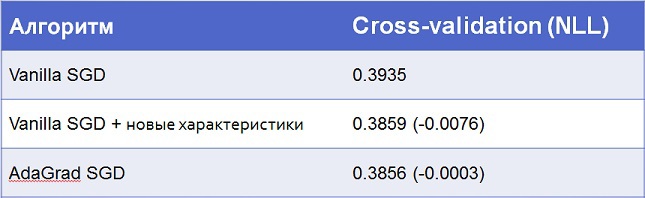
3.2. Трансформация данных для логистической регрессии
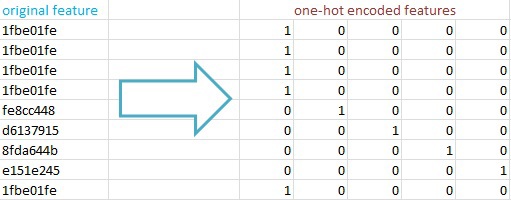
Чтобы алгоритм логистической регрессии мог работать с данными (а они представлены в формате текстовых значений), их необходимо преобразовать в скалярные значения. Я использовал one-hot encoding: преобразование текстовых характеристик в матрицу NxM cо значениями «0» и «1», где N – это кол-во записей, а M – кол-во уникальных значений у этой характеристики. Основные причины – сохраняется максимум информации, а feature hashing позволяет быстро работать с пространствами с миллионами характеристик в рамках логистической регрессии.
4. Матрикснет – сборка в домашних условиях
После того, как я получил неплохие результаты с логистической регрессией, необходимо было дальше улучшаться. Мне было интересно разобраться в том, как работает Матрикснет Яндекса, более того, я ожидал от него хороших результатов (всё-таки это его одна из задач – предсказывать CTR внутри Яндекса для рекламной выдачи в поиске). Если собрать всю публично доступную информацию о Матрикснете (см. полный список ссылок в конце статьи), то можно воссоздать его алгоритм. Я не претендую на то, что именно в таком виде алгоритм работает внутри Яндекса, я этого не знаю, но в своём коде и в этой статье использовал все найденные «фишки» и намёки на них.
Пойдём по порядку, из чего состоит Мактрикснет:
- Базовый элемент – Classification and Regression Tree (CART);
- Основной алгоритм – Gradient Boosting Machine (GBM)
- Апдейт основного алгоритма – Stochastic Gradient Boosting Machine (SGBM).
4.1. Classification and Regression Tree (CART)
Это один из классических алгоритмов дерева решений, о котором уже писали на Хабре (например, тут и тут). Поэтому не буду уходить в детали, лишь напомню принцип работы и основные термины.
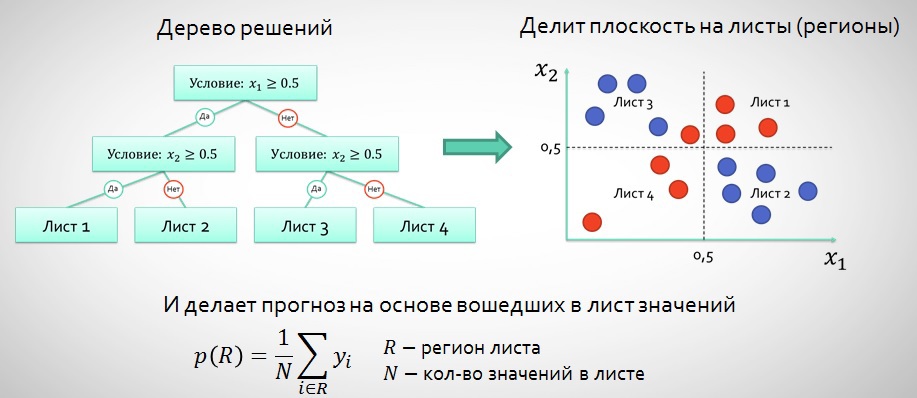
Таким образом, у дерева решений есть следующие параметры, определяющие алгоритм:
- Условия сплита на листы (x_1≥0.5)
- «Высота» дерева (кол-во уровней с условиями, в примере выше их 2)
- Правило прогнозирования p® (в примере выше используется математическое ожидание)
4.1.1. Как определить характеристику для условия сплита
На каждом уровне нам необходимо определить характеристику для условия сплита, который разделит плоскость таким образом, что мы будем делать более точные прогнозы.

Таким образом проходим по всем характеристикам и возможным сплитам и выбираем те точки, где у нас будет ниже значение NLL после сплита (в примере выше это, конечно, x2). Для определения сплита обычно используются другие функции – information gain и Gini impurity, однако в нашем случае мы выбираем NLL, так как именно это просили нас минимизировать в задании (см. описание задания в разделе №1).
4.1.2. Регуляризация в CART
В случае с CART обычно необходима регуляризация, чтобы не делать слишком уверенные предсказания там, где мы на самом деле не уверены. Яндекс предлагает скорректировать формулу предсказания следующим образом:
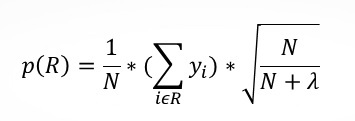
Где N – кол-во значений в листе, а лямбда – регуляризационный параметр (специалисты Мактрикснета рекомендуют 100, но нужно тестировать под каждую задачу отдельно). Таким образом, чем меньше у нас значений в листе, тем меньше наш алгоритм будет уверен в предсказываемом значении.
4.1.3. Забывчивые деревья (Oblivious Trees)
В Матрикснете вместо классического подхода, когда после сплита по x1 следующий уровень дерева не может делить данные по этой характеристике, используются т.н. забывчивые деревья, которые могут в рамках нескольких уровней сплитить значения по одной и той же характеристике (как будто «забывая», что по ней сплит уже был сделан).
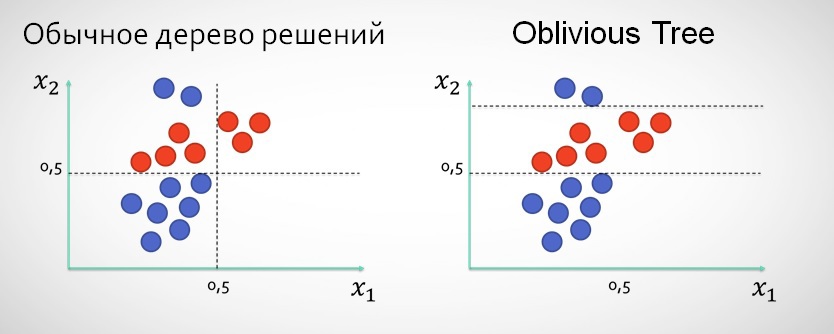
Использование этого типа деревьев, на мой взгляд, обосновано прежде всего в тех случаях, когда в данных есть 1-2 характеристики, более узкие сплиты по которым дают лучше результаты, чем сплиты по ещё не использованным характеристикам.
4.2. Gradient Boosting Machine
Gradient Boosting Machine (GBM) – это использование леса коротких деревьев, где каждое последующее не пытается угадать целевое значение, а пытается улучшить прогноз предыдущих деревьев. Рассмотрим простой пример с регрессией и деревьями с высотой 1 (можем делать только 1 сплит в рамках каждого дерева).

По сути каждое дерево помогает оптимизировать функцию квадратичной ошибки:
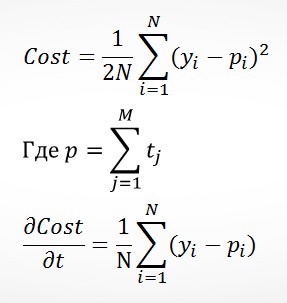
Основное преимущество GBM по сравнению с CART – это меньшая вероятность переобучения, так как мы даём прогнозы на основании листов с бОльшим кол-вом значений. В Матрикснете в GBM «высота» дерева зависит от текущей итерации: начинается с 1, каждые 10 итераций увеличивается ещё на 1, но никогда не превышает 6. Этот подход позволяет существенно разогнать алгоритм, не сильно ухудшая результат на первых итерациях. Я тестировал этот вариант, но остановился на варианте, когда переход на следующий уровень осуществляется после исчерпания возможностей на предыдущем.
4.2.1. GBM для классификации
При работе с классификацией каждое последующее дерево должно улучшать предсказание предыдущего, однако делать это нужно таким образом, чтобы деревья работали на одну задачу – классификацию с помощью сигмоид функции. В этом случае удобно представить задачу оптимизации такой же, как в логистической регрессии, а именно:
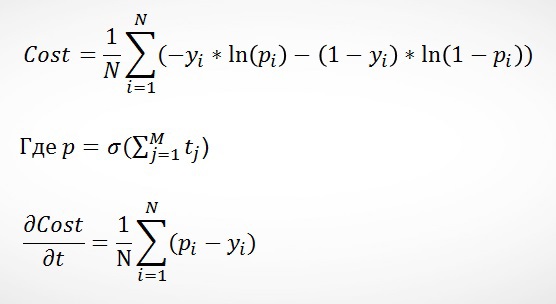
Интересным решением Яндекса является то, что в качестве первоначального прогноза p0 используются предсказания логистической регрессии, а произведения весов и характеристик (wTx) — в качестве одной из характеристик.
4.3. Stochastic GBM
Stochastic GBM отличается от обычного GBM тем, что каждое дерево считается на выборке из данных (10-50%). Это помогает одновременно убить 2-х зайцев – ускорить работу алгоритма (иначе нам бы пришлось просчитывать результат для всех 40,4 млн. тренировочных записей), а также в значительной степени избавиться от проблемы перетренированности.
Финальный результат:
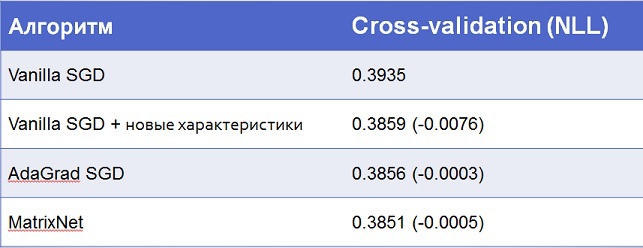
Как видно, всё-таки самую большую оптимизацию даёт работа с данными, а не сами по себе алгоритмы. Хотя с обычной логистической регрессией было бы сложно подняться выше 30-го места, где счёт идёт на каждую десятитысячную.
5. Попытки ускорить машинное обучение в Python
Это был мой первый проект реализации алгоритмов машинного обучения собственными силами, то есть в коде, которым делал предсказания, не используются готовые сторонние решения, все алгоритмы и манипуляции с данными происходят в открытую, что позволило мне лучше понять суть задачи и принципы работы этих инструментов. Однако я пользовался наработками: логистическая регрессия в значимой степени – код Абнишека на Kaggle, Матрикснет заимствует небольшую часть CART из кода Стивена Маршала к книге Machine Learning: Algorithmic Perspective.
С точки зрения реализации, я начинал экспериментировать с задачей в R, но потом быстро отказался от него, так как практически невозможно работать с большими данными. Python был выбрал из-за простоты синтаксиса и наличия большого кол-ва библиотек для машинного обучения.
Основная проблема CPython – он ОЧЕНЬ медленный (хотя и гораздо быстрее R). Однако есть много опций для его ускорения, в результате использовал следующие:
- PyPy – JIT-компилятор, который позволяет ускорить стандартный CPython x20 раз, основная проблема – нет практически никаких библиотек для работы с вычислениями (NumPyPy всё ещё в разработке), всё нужно писать без них. Прекрасно подходило для реализации логистической регрессии со стохастическим градиентным спуском, как в нашем случае;
- Numba – декораторы jit позволяют пре-компилировать некоторые функции (принцип, как в PyPy), однако остальной код может использовать все преимущества библиотек CPython. Большой плюс – для прекомпилированных функций можно снимать GIL (Global Interpreter Lock) и использовать несколько cpu. Что я и использовал для ускорения Матрикснета. Проблема у Numba такая же, как и у PyPy, — нет поддержки никаких библиотек, главное отличие – у Numba есть реализация некоторых функций NumPy.
До Cython не дошёл, так как старался ускориться минимальной кровью, но, думаю, в следующий раз проще переходить сразу на GPGPU с помощью Theano / Numba.
Полный код всех преобразований с данными и самими алгоритмами обучения лежит здесь. Disclaimer: код не оптимизирован, предназначен только для изучения самих алгоритмов.
Если вы нашли любые неточности или ошибки в статье или коде, пишите в личку.
Ссылки на источники, использовавшиеся для статьи и при работе над алгоритмами:
- Логистическая регрессия и многое другое — www.coursera.org/course/ml
- Алгоритмы машинного обучения — seat.massey.ac.nz/personal/s.r.marsland/MLBook.html
- Adaptive Gradient — www.magicbroom.info/Papers/DuchiHaSi10.pdf
- Gradient Boosting Machine — statweb.stanford.edu/~jhf/ftp/trebst.pdf
- Stochastic Gradient Boosting — statweb.stanford.edu/~jhf/ftp/stobst.pdf
- Мактрикснет от Гулина — www.slideshare.net/yandex/matrixnet
- Мактрикснет от Трофимова — wan.poly.edu/KDD2012/forms/workshop/ADKDD12/doc/a3.pdf
- Мактрикснет с ANN в основе — arxiv.org/pdf/1412.6601.pdf
Автор: IvanLobov






