Расчёт параметров пределителя для 8250-совместимых USART

Сегодняшним вечером я расскажу сказку о том, как можно эффективно вычислить параметры пределителя, который обычно используется для задания тактовой частоты USART портов, в частности 8250-совместимых, установленных в Intel SoC.

На текущий момент существует как минимум две линейки Intel SoC, в которых применяется USART с дробным пределителем

1. Medfield, CloverTrail, Tangier
2. BayTrail, Braswell

В чём между ними разница я расскажу чуть позже.

Ниже представлены формулы, по которым вычисляется Fusart — тактовая частота USART, и baud — скорость передачи.

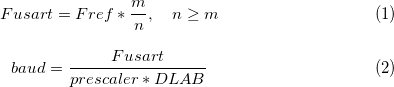
Остальные
Fref — частота до пределителя, m — числитель, n — знаменатель рациональной дроби пределителя, prescaler — целое число, на которое делится Fusart, DLAB — 16-разрядный делитель, представленный в 8250-совместимых чипах.

Из всего набора нам известны только две величины, а именно: Fref и baud. Величина prescaler как правило равна 16 и в некоторых чипах отсутствует возможность её изменять (именно этим отличаются линейки Intel SoC друг от друга)

Расчёт величины prescaler

Поскольку мы работаем с дробным пределителем, а не с полноценной PLL, то из (1) следует

И следовательно мы можем уже вычислить значение prescaler

prescaler = 16

# Made by this way for better understanding that is do-while loop in C
while True:
    fusart = baud * prescaler
    if fusart < fref:
        break
    prescaler -= 1
    if (prescaler == 1):
        break;

Вычисление Fusart

Предыдущая часть работает только в том случае, если не выполняется (3). В противном же случае Fusart может оказаться сильно низкой относительно Fref при запрашиваемой довольно низкой скорости передачи, например 110 бод.

А поскольку числитель и знаменатель делителя как правило равной ширины (в битах), то неплохо бы ограничить их расхождение. Для этого приблизим Fusart к Fref насколько возможно.

fusart <<= int(math.log(fref / fusart, 2))

Почему выбрано именно такое приближение? Дело вот в чём, если у нас возникнет переполнение DLAB, а он всего 16-разрядный, то в случае использования степени двойки мы простейшими битовыми операциями можем это отследить.

Очередь за знаменателем

Очевидно, что теперь из (1,2), следует простая пропорция

Таким образом мы легко вычисляем числитель и знаменатель рациональной дроби пределителя.

divisor = gcd(fref, fusart)
n = fref / divisor
while n > (2 ** width):
    divisor <<= 1
    n >>= 1
m = fusart / divisor

Здесь width — ширина в битах числителя и знаменателя.

Вот собственно и всё. Для желающих исходник на Python можно найти на GitHub Gist.

Автор: andy_shev

Источник