Мотивированный статьей пользователя BubaVV про предсказание веса модели Playboy по ее формам и росту, автор решил углубиться if you now what I mean в эту будоражащую кровь тему исследования и в тех же данных найти выбросы, то есть особо сисястые модели, выделяющиеся на фоне других своими формами, ростом или весом. А на фоне этой разминки чувства юмора заодно немного рассказать начинающим исследователям данных про обнаружение выбросов (outlier detection) и аномалий (anomaly detection) в данных с помощью реализации одноклассовой машины опорных векторов (One-class Support Vector Machine) в библиотеке Scikit-learn, написанной на языке Python.
Загрузка и первичный анализ данных
Итак, по-честному сославшись на первоисточник данных и человека, который над ними поработал, откроем CSV-файл с данными girls.csv и посмотрим, что там есть. Видим параметры 604-х девушек месяца Playboy с декабря 1953 по январь 2009: охват груди (Bust, в см), охват талии (Waist, в см), охват бедер (Hips, в см), а также рост (Height, в см.) и вес (Weight, в кг).
Откроем нашу любимую среду программирования для Python (в моем случае Eclipse + PyDev) и загрузим данные с помощью библиотеки Pandas. В этой статье предполагается, что библиотеки Pandas, NumPy, SciPy, sklearn и matplotlib установлены. Если нет, пользователи Windows могут порадоваться и элементарно установить прекомпилированные библиотеки отсюда.
Ну а пользователям никсов и маков (как и автору) придется чуть-чуть помучаться, но статья не об этом.
Вначале импортируем модули, которые нам понадобятся. Об их роли будем говорить по мере поступления.
import pandas
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.font_manager
from scipy import stats
from sklearn.preprocessing import scale
from sklearn import svm
from sklearn.decomposition import PCA
Создаем экземпляр girls структуры данных DataFrame модуля Pandas считыванием данных из файла girls.csv (он лежит рядом с данным py-файлом, иначе надо указывать полный путь). Параметр header говорит, что названия признаков находятся в первой строке (т.е. в нулевой, если считать, как программисты).
girls = pandas.read_csv('girls.csv', header=0)
Кстати, Pandas — отличный вариант для тех, кто привык к питону, но все еще любит быстроту парсинга данных в R. Главное, что унаследовал Pandas от R — это как раз удобную структуру данных DataFrame.
Автор знакомился с Pandas по тьюториалу Kaggle в пробном соревновании «Titanic: Machine Learning from Disaster». Для тех, кто не знаком с Kaggle, — отличный повод наконец сделать это.
Посмотрим общую статистику наших девушек:
print girls.info()
Нам сообщат, что в нашем распоряжении 604 девушки, каждая с 7-ю признаками — Month (тип object), Year (тип int64) и еще 5-ю признаками типа int64, которые мы уже называли.
Дальше узнаем про девушек побольше:
print girls.describe()
Эх, если бы в жизни все было так просто!
Интерпретатор нам перечислит основные статистические характеристики признаков девушек — среднее, минимальное и максимальное значения. Уже неплохо. Отсюда заключаем, что средние формы модели Playboy 89-60-88 (ожидаемо), средний рост — 168 см, вес — 52 кг.
Вот рост то, кажется, маловат. Видимо, объясняется тем, что данные исторические, с середины ХХ века, сейчас-то стандартом у моделей, кажется, считается рост 180 см.
Охват груди девушек меняется от 81 до 104 см, талия — от 46 до 89, бедра — от 61 до 99, рост — от 150 см до 188 см, вес — от 42 кг до 68 кг.
Ух ты, уже можно подозревать, что в данные вкралась ошибка. Это что за пивная бочка модель с талией 89 см? А как бедра могут быть 61 см?
Давайте посмотрим, что это за уникумы:
print girls[['Month','Year']][girls['Waist'] == 89]
Это девушки месяца Playboy в декабре 1998-го и январе 2005-го соответственно. Несложно их отыскать здесь. Это тройняшки Николь, Эрика и Жаклин с неговорящей фамилей Дам (Dahm) — все три «под одним аккаунтом» и Дэстини Дэвис (Destiny Davis). Легко заметить, что талии тройняшек — 25 дюймов (64 см), а не 89, а бедра нашей Дэстини — 86 см, а никак не 61.
Для красоты можно еще построить и гистограммы распределения параметров девушек (для разнообразия они сделаны в R).
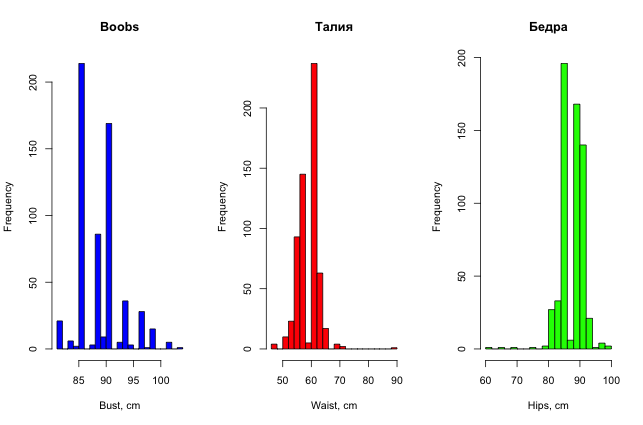
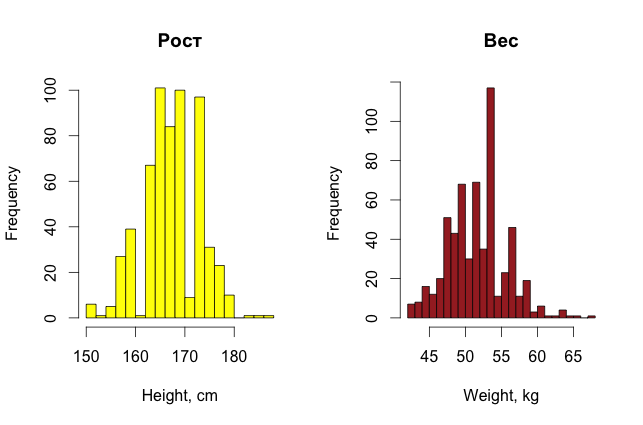
Итак, простым, невооруженным взглядом на данные уже можно найти в них какие-то странности, если, конечно, данных не очень много, и признаки можно как-то трактовать в понятном человеку виде.
Предобработка данных
Для обучения модели оставим только численные параметры, кроме года. Запишем их в массив NumPy girl_params, попутно преобразовав к типу float64. Шкалируем данные так, чтобы все признаки лежали в диапазоне от -1 до 1. Это важно для многих алгоритмов маишинного обучения. Не вдаваясь в детали, шкалированием мы избегаем того, что признак получает больший вес только из-за того, что у него больший диапазон изменения. Например, если по признакам «Возраст» и «Доход» считать Евклидово расстояние между людьми, то у дохода вклад в метрику будет намного выше только из-за того, что он измеряется, например, в тысячах, а возраст в десятках.
girl_params = np.array(girls.values[:,2:], dtype="float64")
girl_params = scale(girl_params)
Далее выделяем 2 главных компонента в данных, чтоб их можно было отобразить. Тут нам пригодилась библиотека Scikit-learn Principal Component Analysis (PCA). Также нам не помешает сохранить число наших девушек. Кроме того, мы скажем, что ищем 1% выбросов в данных, то есть ограничимся 6-7 «странными» девушками. (Переменные в Питоне, записанные в верхнем регистре, символизируют константы и обычно записываются в начале файла после подключения модулей).
X = PCA(n_components=2).fit_transform(girl_params)
girls_num = X.shape[0]
OUTLIER_FRACTION = 0.01
Обучение модели
Для обнаружения «выбросов» в данных используем одноклассовую модель машины опорных векторов. Теоретическую работу над этой вариацией SVM начал Алексей Яковлевич Червоненкис. Как заявляет «Яндекс», сейчас разработка методов решения этой задачи занимает первое место в развитии теории машинного обучения.
Не буду здесь рассказывать, что такое SVM и ядра, про это и так много написано, например на Хабре (попроще) и на machinelearning.ru (посложнее). Отмечу только, что One-class SVM позовляет, как это следует из названия, отличать объекты одного класса. Обнаружение аномалий в данных — всего лишь скромное приложение этой идеи. Сейчас, в эпоху глубинного обучения, с помощью алгоритмов одноклассовой классификации пытаются научить компьютер «создавать представление» предмета, как, например, ребенок отличает собаку от всех остальных предметов.
Но вернемся к Scikit-реализации One-class SVM, которая неплохо документирована на сайте Scikit-learn.
Создаем экземпляр классификатора с гауссовым ядром и «скармливаем» ему данные.
clf = svm.OneClassSVM(kernel="rbf")
clf.fit(X)
Поиск выбросов
Создаем массив dist_to_border, который хранит расстояния от объектов обучающей выборки X до построенной разделяющей поверхности, а затем, после того, как мы выбрали порог, создаем массив индикаторов (True или False) того, что объект является представителем данного класса, а не выбросом. При этом расстояние положительно, если объект лежит «внутри» области, ограниченной построенной разделяющей поверхностью (т.е. является представителем класса), и отрицательно в противном случае. Порог определяется статистически, как такое расстояние до разделяющей поверхности, что у OUTLIER_FRACTION (в нашем случае у одного) процента выборки оно больше (т.е в нашем случае, threshold — это 1%-перцентиль массива расстояний до разделяющей поверхности).
dist_to_border = clf.decision_function(X).ravel()
threshold = stats.scoreatpercentile(dist_to_border,
100 * OUTLIER_FRACTION)
is_inlier = dist_to_border > threshold
Отображение и трактовка результатов
Наконец, визуализируем то что получилось. На этом моменте я не буду останавливаться, разобраться с matplotlib желающие могут самостоятельно. Это переработанный код из примера Scikit-learn «Outlier detection with several methods».
xx, yy = np.meshgrid(np.linspace(-7, 7, 500), np.linspace(-7, 7, 500))
n_inliers = int((1. - OUTLIER_FRACTION) * girls_num)
n_outliers = int(OUTLIER_FRACTION * girls_num)
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.title("Outlier detection")
plt.contourf(xx, yy, Z, levels=np.linspace(Z.min(), threshold, 7),
cmap=plt.cm.Blues_r)
a = plt.contour(xx, yy, Z, levels=[threshold],
linewidths=2, colors='red')
plt.contourf(xx, yy, Z, levels=[threshold, Z.max()],
colors='orange')
b = plt.scatter(X[is_inlier == 0, 0], X[is_inlier == 0, 1], c='white')
c = plt.scatter(X[is_inlier == 1, 0], X[is_inlier == 1, 1], c='black')
plt.axis('tight')
plt.legend([a.collections[0], b, c],
['learned decision function', 'outliers', 'inliers'],
prop=matplotlib.font_manager.FontProperties(size=11))
plt.xlim((-7, 7))
plt.ylim((-7, 7))
plt.show()
Получаем такую картинку:
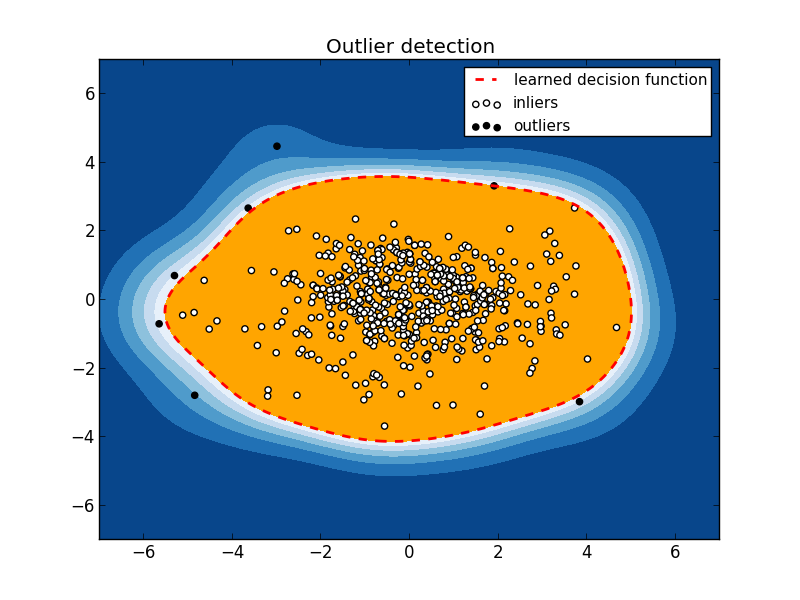
Видны 7 «выбросов». Чтобы понять, что за девушки таятся под этим нелицеприятным «выбросы», посмотрим их в исходных данных.
print girls[is_inlier == 0]
Month Year Bust Waist Hips Height Weight
54 September 1962 91 46 86 152 45
67 October 1963 94 66 94 183 68
79 October 1964 104 64 97 168 66
173 September 1972 98 64 99 185 64
483 December 1998 86 89 86 173 52
507 December 2000 86 66 91 188 61
535 April 2003 86 61 69 173 54
А теперь самая занимательная часть — трактовка полученных выбросов.
Замечаем, что экспонатов в нашей кунсткамере всего 7 (мы так удачно задали порог OUTLIER_FRACTION), поэтому можно пройтись по каждому из них.
- Мики Уинтерс. Сентябрь, 1962. 91-46-86, рост 152, вес 45.

Талия 46 — это, конечно, круто! Как у них при этом грудь 91? - Кристин Уильямс. Октябрь, 1963. 94-66-94, рост 183, вес 68.

Не маленькая девушка для тех лет. Это тебе не Мики Уинтерс. - Розмари Хилкрест. Октябрь, 1964. 104-64-97, рост 168, вес 66.

Воу-воу, палехче!Внушительная дама. - Сюзан Миллер. Сентябрь, 1972. 98-64-99, рост 185, вес 64.

- Милашки-тройняшки Дам. 86-89 (реально 64)-86, рост 173, вес 52.

Пример ошибки в данных. Не очень понятно, как им все на троих мерили. - Кара Мишель. Декабрь, 2000. 86-66-91, рост 188, вес 61.

Ростом 188 — выше автора этой статьи. Явный «выброс» для таких «исторических» данных. - Кармелла де Сезаре. Апрель, 2003. 86-61-69, рост 173, вес 54.

Пожалуй, из-за бедер.
Примечательно, что дама с охватом бедер в 61 см, которую мы подозревали в сильном отличии от прочих девушек, по остальным параметрам вполне в норме, и SVM-ом не была определена как «выброс».
Заключение
Напоследок отмечу важность первичного анализа данных, «просто глазами» и, конечно, отмечу, что обнаружение аномалий в данных применяется и в более серьезных задачах — в кредитном скоринге, чтоб распознать неблагонадежных клиентов, в системах безопасности для обнаружения потенциальных «узких мест», при анализе банковских транзакций для поиска злоумышленников и не только. Заинтересованный читатель найдет и множество других алгоритмов обнаружения аномалий и выбросов в данных и их применений.
Автор: yorko






