Предисловие
Область, в которой мне повезло работать, называется вычислительная электрофизиология сердца. Физиология сердечной деятельности определяется электрическими процессами, происходящими на уровне отдельных клеток миокарда. Эти электрические процессы создают электрическое поле, которое достаточно легко измерить. Более того оно очень неплохо описывается в рамках математических моделей электростатики. Тут и возникает уникальная возможность строго математически описать работу сердца, а значит — и усовершенствовать методы лечения многих сердечных заболеваний.
За время работы в этой области у меня накопился некоторый опыт использования различных вычислительных технологий. На некоторые вопросы, которые могут быть интересны не только мне, я постараюсь отвечать в рамках этой публикации.
Кратко о Scientific Python
Начиная еще с первых курсов университета, я пытался найти идеальный инструмент для быстрой разработки численных алгоритмов. Если отбросить ряд откровенно маргинальных технологий, я курсировал между C++ и MATLAB. Это продолжалось до тех пор, пока я не открыл для себя Scientific Python [1].
Scientific Python представляет собой набор библиотек языка Python для научных вычислений и научной визуализации. В своей работе я использую следующие пакеты, которые покрывают примерно 90% моих потребностей:
| Название | Описание |
|---|---|
| NumPy | Одна из базовых библиотек, позволяет работать с многомерными массивами как с едиными объектами в MATLAB стиле. Включает реализацию основных процедур линейной алгебры, преобразование Фурье, работу со случайными числами и др. |
| SciPy | Расширение NumPy, включает реализацию методов оптимизации, работу с разряженными матрицами, статистику и др. |
| Pandas | Отдельный пакет для анализа многомерных данных и статистики. |
| SymPy | Пакет символьной математики. |
| Matplotlib | Двумерная графика. |
| Mayavi2 | Трехмерная графика на основе VTK. |
| Spyder | Удобная IDE для интерактивной разработки математических алгоритмов. |
В Scientific Python я нашел для себя великолепный баланс между удобной высокоуровневой абстракцией для быстрой разработки численных алгоритмов и современным развитым языком. Но, как известно, не бывает идеальных инструментов. И одна из достаточно критических проблем в Python — это проблема параллельных вычислений.
Проблемы параллельных вычислений в Python.
Под параллельными вычислениями в этой статье я буду понимать SMP — симметричный мультипроцессинг с общей памятью. Вопросов использования CUDA и систем с раздельной памятью (чаще всего используется стандарт MPI) касаться не буду.
Проблема заключается в GIL. GIL (Global Interpreter Lock) — это блокировка (mutex), которая не позволяет нескольким потокам выполнить один и тот же байткод. Эта блокировка, к сожалению, является необходимой, так как система управления памятью в CPython не является потокобезопасной. Да, GIL это не проблема языка Python, а проблема реализации интерпретатора CPython. Но, к сожалению, остальные реализации Python не слишком приспособлены для создания быстрых численных алгоритмов.
К счастью, в настоящее время существует несколько способов решения проблем GIL. Рассмотрим их.
Тестовая задача
Даны два набора по N векторов: P={p1,p2,…,pN} и Q={q1,q2,…,qN} в трехмерном евклидовом пространстве. Необходимо построить матрицу R размерностью N x N, каждый элемент ri,j которой вычисляется по формуле:
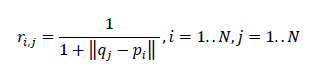
Грубо говоря, нужно вычислить матрицу, использующую попарные расстояния между всеми векторами. Эта матрица достаточно часто используется в реальных расчетах, например, при RBF интерполяции или решении дифуров в чп методом интегральных уравнений.
В тестовых экспериментах количество векторов N = 5000. Для вычислений использовался процессор с 4 ядрами. Результаты получены по среднему времени из 10 запусков.
Полную реализацию тестовых задач можно поглядеть на GitHub [2].
Параллельная реализация на C++
Для сравнения эффективности параллельных вычислений на Python, я реализовал эту задачу на C++. Код основной функции выглядит следующий образом.
Однопроцессорная реализация:
//! Single thread matrix R calculation
void spGetR(vector<Vector3D> & p, vector<Vector3D> & q, MatrixMN & R)
{
for (int i = 0; i < p.size(); i++) {
Vector3D & a = p[i];
for (int j = 0; j < q.size(); j++) {
Vector3D & b = q[j];
Vector3D r = b - a;
R(i, j) = 1 / (1 + sqrt(r * r));
}
}
}
Многопроцессорная реализация:
//! OpenMP matrix R calculations
void mpGetR(vector<Vector3D> & p, vector<Vector3D> & q, MatrixMN & R)
{
#pragma omp parallel for
for (int i = 0; i < p.size(); i++) {
Vector3D & a = p[i];
for (int j = 0; j < q.size(); j++) {
Vector3D & b = q[j];
Vector3D r = b - a;
R(i, j) = 1 / (1 + sqrt(r * r));
}
}
}
Что здесь интересного? Ну прежде всего я использовал отдельный класс Vector3D для представления вектора в трехмерном пространстве. Перегруженный оператор "*" в этом классе имеет смысл скалярного произведения. Для представления набора векторов я использовал std::vector. Для параллельных вычислений использовалась технология OpenMP. Для параллелизации алгоритма достаточно использовать директиву "#pragma omp parallel for".
Результаты:
| Однопроцессорный С++ | 224 ms |
| Многопроцессорный C++ | 65 ms |
Ускорение в 3.45 раза при параллельном расчете я считаю вполне неплохим для четырехядерного процессора.
Параллельные реализации на Python
1.Наивная реализация на чистом Python
В этом тесте хотелось проверить сколько будет решаться задача на чистом Python без использования каких-либо специальных пакетов.
Код решения:
def sppyGetR(p, q):
R = np.empty((p.shape[0], q.shape[1]))
nP = p.shape[0]
nQ = q.shape[1]
for i in xrange(nP):
for j in xrange(nQ):
rx = p[i, 0] - q[0, j]
ry = p[i, 1] - q[1, j]
rz = p[i, 2] - q[2, j]
R[i, j] = 1 / (1 + sqrt(rx * rx + ry * ry + rz * rz))
return R
Здесь p, q – входные данные в формате NumPy массивов размерностями (N, 3) и (3, N). А дальше идет честный цикл на Python, вычисляющий элементы матрицы R.
Результаты:
| Однопроцессорный Python | 57 386 ms |
Да, да, именно 57 тысяч миллисекунд. Где-то в 256 раз медленнее однопроцессорного C++. В общем, это совсем не вариант для численных расчетов.
2 Однопроцессорный NumPy
Вообще, для вычислений на Python с использованием NumPy иногда можно вообще не задумываться о параллельности. Так, например, процедура умножения двух матриц на NumPy будет в итоге все-равно выполняться с использованием низкоуровневых высокоэффективных библиотек линейной алгебры на C++ (MKL или ATLAS). Но, к сожалению, это верно лишь для наиболее типовых операций и не работает в общем случае. Наша тестовая задача, к сожалению, будет выполняться последовательно.
Код решения следующий:
def spnpGetR(p, q):
Rx = p[:, 0:1] - q[0:1]
Ry = p[:, 1:2] - q[1:2]
Rz = p[:, 2:3] - q[2:3]
R = 1 / (1 + np.sqrt(Rx * Rx + Ry * Ry + Rz * Rz))
return R
Всего 4 строчки и никаких циклов! Вот за это я и люблю NumPy.
Результаты:
| Однопроцессорный NumPy | 973 ms |
Примерно в 4.3 раза медленнее однопроцессорного C++. Вот это уже совсем неплохой результат. Для подавляющего большинства расчетов этой производительности вполне хватает. Но это все пока однопроцессорные результаты. Идем дальше к мультипроцессингу.
3 Многопроцессорный NumPy
В качестве решения проблем с GIL традиционно предлагается использовать несколько независимых процессов выполнения вместо нескольких потоков выполнения. Все бы хорошо, но есть проблема. Каждый процесс обладает независимой памятью, и нам необходимо в каждый процесс передавать матрицу результатов. Для решения этой проблемы в Python multiprocessing вводится класс RawArray, предоставляющий возможность разделить один массив данных между процессами. Не знаю точно, что лежит в основе RawArray. Мне кажется, что это memory mapped files.
Код решения следующий:
def mpnpGetR_worker(job):
start, stop = job
p = np.reshape(np.frombuffer(mp_share.p), (-1, 3))
q = np.reshape(np.frombuffer(mp_share.q), (3, -1))
R = np.reshape(np.frombuffer(mp_share.R), (p.shape[0], q.shape[1]))
Rx = p[start:stop, 0:1] - q[0:1]
Ry = p[start:stop, 1:2] - q[1:2]
Rz = p[start:stop, 2:3] - q[2:3]
R[start:stop, :] = 1 / (1 + np.sqrt(Rx * Rx + Ry * Ry + Rz * Rz))
def mpnpGetR(p, q):
nP, nQ = p.shape[0], q.shape[1]
sh_p = mp.RawArray(ctypes.c_double, p.ravel())
sh_q = mp.RawArray(ctypes.c_double, q.ravel())
sh_R = mp.RawArray(ctypes.c_double, nP * nQ)
nCPU = 4
jobs = utils.generateJobs(nP, nCPU)
pool = mp.Pool(processes=nCPU, initializer=mp_init, initargs=(sh_p, sh_q, sh_R))
pool.map(mpnpGetR_worker, jobs, chunksize=1)
R = np.reshape(np.frombuffer(sh_R), (nP, nQ))
return R
Мы создаем разделенные массивы для входных данных и выходной матрицы, создаем пул процессов по числу ядер, разбиваем задачу на подзадачи и решаем параллельно.
Результаты:
| Многопроцессорный NumPy | 795 ms |
Да, быстрее однопроцессорного варианта, но всего в 1.22 раза. С ростом числа N эффективность решения растет. Но, в целом и общем, наша тестовая задача не слишком приспособлена для решения в рамках множества независимых процессов с независимой памятью. Хотя для других задач такой вариант может быть вполне эффективным.
На этом известные мне решения для параллельного программирования с использование только Python закончились. Далее, как бы нам не хотелось, для освобождения от GIL придется спускаться на уровень C++. Но этот не так страшно, как кажется.
4 Cython
Cython [3] — это расширение языка Python, позволяющее внедрять инструкции на языке C в код на Python. Таким образом, мы можем взять код на Python и добавлением нескольких инструкций значительно ускорить узкие в плане производительности места. Cython модули преобразуются в код на C и далее компилируются в Python модули. Код решения нашей задачи на Cython следующий:
Однопроцессорный Cython:
@cython.boundscheck(False)
@cython.wraparound(False)
def spcyGetR(pp, pq):
pR = np.empty((pp.shape[0], pq.shape[1]))
cdef int i, j, k
cdef int nP = pp.shape[0]
cdef int nQ = pq.shape[1]
cdef double[:, :] p = pp
cdef double[:, :] q = pq
cdef double[:, :] R = pR
cdef double rx, ry, rz
with nogil:
for i in xrange(nP):
for j in xrange(nQ):
rx = p[i, 0] - q[0, j]
ry = p[i, 1] - q[1, j]
rz = p[i, 2] - q[2, j]
R[i, j] = 1 / (1 + sqrt(rx * rx + ry * ry + rz * rz))
return R
Многопроцессорный Cython:
@cython.boundscheck(False)
@cython.wraparound(False)
def mpcyGetR(pp, pq):
pR = np.empty((pp.shape[0], pq.shape[1]))
cdef int i, j, k
cdef int nP = pp.shape[0]
cdef int nQ = pq.shape[1]
cdef double[:, :] p = pp
cdef double[:, :] q = pq
cdef double[:, :] R = pR
cdef double rx, ry, rz
with nogil, parallel():
for i in prange(nP, schedule='guided'):
for j in xrange(nQ):
rx = p[i, 0] - q[0, j]
ry = p[i, 1] - q[1, j]
rz = p[i, 2] - q[2, j]
R[i, j] = 1 / (1 + sqrt(rx * rx + ry * ry + rz * rz))
return R
Если сравнить данный код с реализацией на чистом Python, то все, что нам пришлось сделать, это всего лишь указать типы для используемых переменных. GIL отпускается одной строчкой. Параллельный цикл организуется всего лишь инструкцией prange вместо xrange. На мой взгляд, вполне несложно и красиво!
Результаты:
| Однопроцессорный Cython | 255 ms |
| Многопроцессорный Cython | 75 ms |
Вау! Время исполнения почти совпадает с временем исполнения на C++. Отставание примерно в 1.1 раз как в однопроцессорном, так и в многопроцессорном вариантах практически незаметно на реальных задачах.
5 Numba
Numba [4] достаточно новая библиотека, находится в активном развитии. Идея здесь примерно такая же, что и в Cython — попытка спуститься на уровень C++ в коде на Python. Но идея реализована существенно элегантнее.
Numba основана на LLVM компиляторах, которые позволяют производить компиляцию непосредственно в процессе исполнения программы (JIT компиляция). Например, для компилирования любой процедуры на Python достаточно всего лишь добавить аннотацию «jit». Более того аннотации позволяют указывать типы входных/выходных данных, что делает JIT-компиляцию существенно более эффективной.
Код реализации задачи следующий.
Однопроцессорный Numba:
@jit(double[:, :](double[:, :], double[:, :]))
def spnbGetR(p, q):
nP = p.shape[0]
nQ = q.shape[1]
R = np.empty((nP, nQ))
for i in xrange(nP):
for j in xrange(nQ):
rx = p[i, 0] - q[0, j]
ry = p[i, 1] - q[1, j]
rz = p[i, 2] - q[2, j]
R[i, j] = 1 / (1 + sqrt(rx * rx + ry * ry + rz * rz))
return R
Многопроцессорный Numba:
def makeWorker():
savethread = pythonapi.PyEval_SaveThread
savethread.argtypes = []
savethread.restype = c_void_p
restorethread = pythonapi.PyEval_RestoreThread
restorethread.argtypes = [c_void_p]
restorethread.restype = None
def worker(p, q, R, job):
threadstate = savethread()
nQ = q.shape[1]
for i in xrange(job[0], job[1]):
for j in xrange(nQ):
rx = p[i, 0] - q[0, j]
ry = p[i, 1] - q[1, j]
rz = p[i, 2] - q[2, j]
R[i, j] = 1 / (1 + sqrt(rx * rx + ry * ry + rz * rz))
restorethread(threadstate)
signature = void(double[:, :], double[:, :], double[:, :], int64[:])
worker_ext = jit(signature, nopython=True)(worker)
return worker_ext
def mpnbGetR(p, q):
nP, nQ = p.shape[0], q.shape[1]
R = np.empty((nP, nQ))
nCPU = utils.getCPUCount()
jobs = utils.generateJobs(nP, nCPU)
worker_ext = makeWorker()
threads = [threading.Thread(target=worker_ext, args=(p, q, R, job)) for job in jobs]
for thread in threads:
thread.start()
for thread in threads:
thread.join()
return R
По сравнению с чистым Python, к однопроцессорному решению на Numba добавляется всего одна аннотация! Многопроцессорный вариант, к сожалению, не так красив. В нем требуется организовывать пул потоков, в ручном режиме отдавать GIL. В предыдущих релизах Numba была попытка реализовать параллельных цикл одной инструкцией, но из-за проблем стабильности в последующих релизах эта возможность была убрана. Я уверен, что с течением времени эту возможность починят.
Результаты выполнения:
| Однопроцессорный Numba | 359 ms |
| Многопроцессорный Numba | 180 ms |
Слегка хуже, чем Cython, но результаты все-равно очень достойные! А само решение крайне элегантное.
Выводы
Результаты я хочу проиллюстрировать следующими диаграммами:
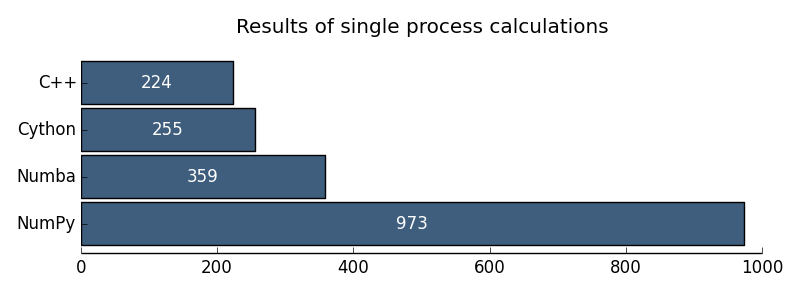
Рис. 1. Результаты однопроцессорных вычислений
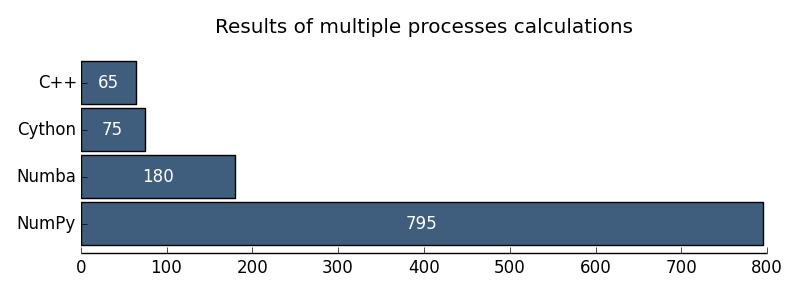
Рис. 2. Результаты многопроцессорных вычислений
Мне кажется, что проблемы GIL в Python для численных расчетов практически преодолены. Пока в качестве технологии параллельных вычислений я бы рекомендовал Cython. Но очень бы внимательно пригляделся бы к Numba.
Ссылки
[1] Scientific Python: scipy.org
[2] Полные исходные коды тестов: github.com/alec-kalinin/open-nuance
[3] Cython: cython.org
[4] Numba: numba.pydata.org
Автор: alec_kalinin