AES-128. Детали и реализация на python

Идея написать для себя что-то шифрующее родилась довольно тривиально — пришлось завести еще одну дебетовую карту и, следовательно, хранить в голове еще один пин-код. Хранить такую информацию в открытом виде паранойя не позволяет, использовать сторонние сервисы тоже, поэтому после некоторых поисков остановился на стандарте AES. Сразу захотелось разобраться и реализовать алгоритм самому, не прибегая к дополнительным модулям.

В статье я расскажу подробно о составляющих алгоритма, немного окунемся в мат часть и приведу пример реализации на python. В разработке я ограничивался только тем, что входит в состав стандартной библиотеки.

Немного введения

Advanced Encryption Standard является общеизвестным названием алгоритма Rijndael ([rɛindaːl]), который был разработан двумя бельгийскими криптографами Йоаном Дайменом и Винсентом Рэйменом. Алгоритм является блочным и симметричным. Принят в качестве стандарта шифрования данных для гос учреждений в США. Нашумевшее в последнее время Агенство Национальной Безопасности использует его для хранения документов: вплоть до уровня SECRET применяется шифрование с ключом длиной в 128 бит, информация TOP SECRET требует ключа в 192 или 256 бит. В дополнение к высокой криптостойкости алгоритм базируется на не самой сложной математике.

Много шифрования

Для работы нам необходим набор байтов в качестве объекта шифрования и секретный ключ, который потребуется при расшифровке. Длинные ключи хранить в голове неудобно, да и считается, что длины ключа в 128 бит, с лихвой хватает для неприступности, поэтому на варианты 192/256 я не смотрел. К тому же, как сказано здесь, при некоторых условиях более длинный ключ может отставать в устойчивости.

Введем некоторые обозначения:

• State — промежуточный результат шифрования, который может быть представлен как прямоугольный массив байтов имеющий 4 строки и Nb колонок. Каждая ячейка State содержит значение размером в 1 байт
• Nb — число столбцов (32-х битных слов), составляющих State. Для стандарта регламентировано Nb = 4
• Nk — длина ключа в 32-х битных словах. Для AES, Nk = 4, 6, 8. Мы уже определились, что будем использовать Nk = 4
• Nr — количество раундов шифрования. В зависимости от длины ключа, Nr = 10, 12 или 14

Алгоритм имеет четыре трансформациями, каждая из которых своим образом влияет на состояние State и в конечном итоге приводит к результату: SubBytes(), ShiftRows(), MixColumns() и AddRoundKey(). Общую схему шифрования можно представить как:

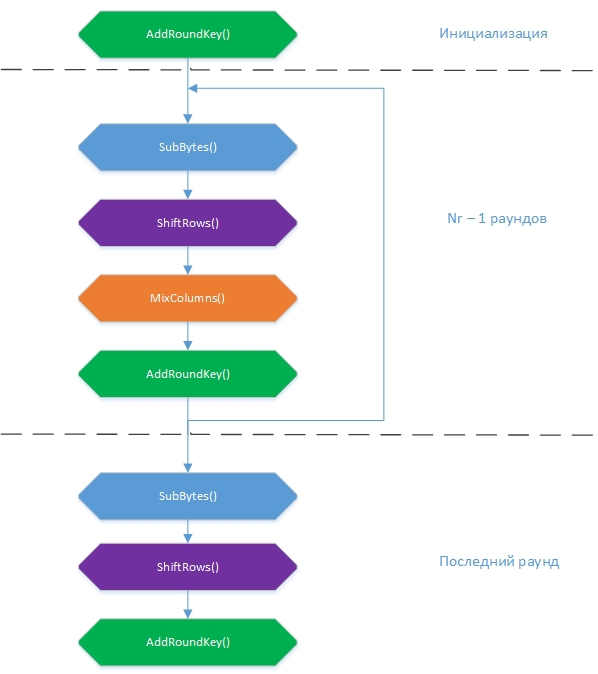
В начале заполняется массив State входными значениями по формуле State[r][c] = input[r + 4c], r = 0,1...4; c = 0,1..Nb. То есть по колонкам. За раз шифруется блок размером 16 байт.

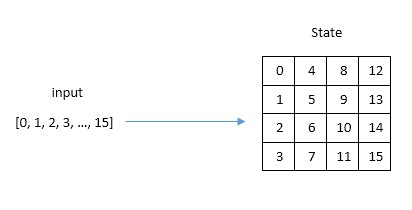
Алгоритм оперирует байтами, считая их элементами конечного поля или поля Галуа GF(2⁸). Число в скобках — это количество элементов поля или его мощность. Элементами поля GF(2⁸) являются многочлены степени не более 7, которые могут быть заданы строкой своих коэффициентов. Байт очень легко представить в виде многочлена. Например, байту {1,1,1,0,0,0,1,1} соответствует элемент поля 1x⁷ + 1x⁶ + 1x⁵ + 0x⁴ + 0x³ + 0x² + 1x¹ + 1x⁰ = 1x⁷ + 1x⁶ + 1x⁵ + x +1. То, что мы работаем с элементами поля, очень важно потому, что это меняет правила операций сложения и умножения. Этого мы коснемся немного позже.

Далее рассмотрим подробно каждую из трансформаций.

SybButes()

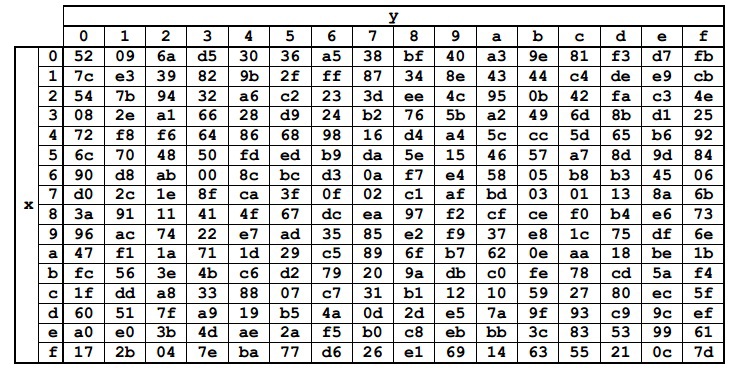
Преобразование представляет собой замену каждого байта из State на соответствующий ему из константной таблицы Sbox. Значения элементов Sbox представлены в шестнадцатеричной системе счисления. Сама же таблица получена посредством преобразований уже известного нам поля GF(2⁸)

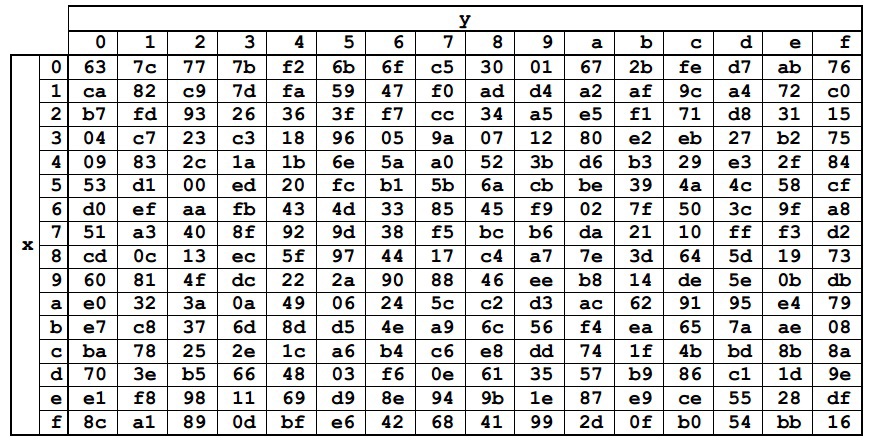
Каждый байт из State можно представить как {xy} в шестнадцатеричной системе счисления. Тогда следует заменять его на элемент, стоящий на пересечении строки x и столбца y. Например, {6е} заменится на {9f}, а {15} на {59}.

ShiftRows()

Простая трансформация. Она выполняет циклический сдвиг влево на 1 элемент для первой строки, на 2 для второй и на 3 для третьей. Нулевая строка не сдвигается.

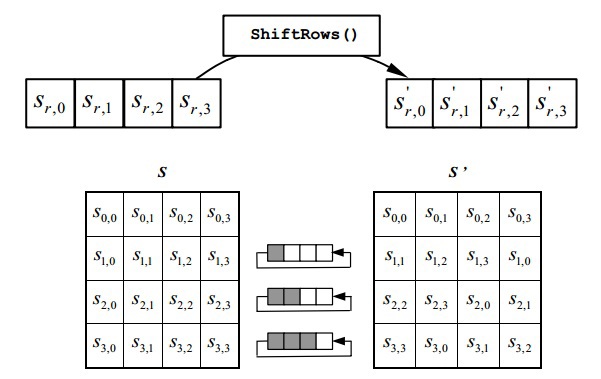
MixColumns()

В рамках этой трансформации каждая колонка в State представляется в виде многочлена и перемножается в поле GF(2⁸) по модулю x⁴ + 1 с фиксированным многочленом 3x³ + x² + x + 2. Звучит вроде просто, но малопонятно, как это сделать. Картина становится проще, если посмотреть на эквивалентную матричную запись, предоставленную в официальном документе стандарта:

При умножении матриц, значение а_ij получается как сумма произведений соответствующих элементов i-ой строки первой матрицы и j-ого столбца второй, т. е.

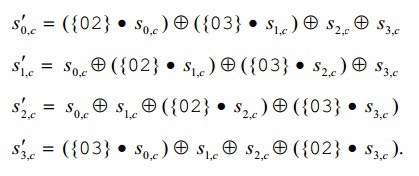
Здесь нужно вспомнить о неработоспособности обычных правил сложения и умножения.
Новые правила:

• Сложение в поле GF(2⁸) эквивалентно операции XOR
• Умножение на {01} не меняет умножаемое
• Умножение на {02} производится по правилу: если умножаемое значение меньше {80}, оно сдвигается влево на 1 бит. Если же умножаемое значение больше или равно {80}, оно сначала сдвигается влево на 1 бит, а затем к результату сдвига применяется операция XOR со значением {1b}. Результат может перескочить за значение {ff}, то есть за границы одного байта. В этом случае нужно вернуть остаток от деления результата на {100}.
• Умножение на другие константы можно выразить через предыдущие

Естественно, это не общие правила арифметики в конечном поле, но в рамках алгоритма придется умножать на три константы при шифровании и на четыре при дешифровке, так что таких локальных лайфхаков вполне хватит.
MixColumns() вместе с ShiftRows() добавляют диффузию в шифр.

AddRoundKey()

Трансформация производит побитовый XOR каждого элемента из State с соответствующим элементом из RoundKey. RoundKey — массив такого же размера, как и State, который строится для каждого раунда на основе секретного ключа функцией KeyExpansion(), которую и рассмотрим далее.

KeyExpansion()

Эта вспомогательная трансформация формирует набор раундовых ключей — KeySchedule. KeySchedule представляет собой длинную таблицу, состоящую из Nb*(Nr + 1) столбцов или (Nr + 1) блоков, каждый из которых равен по размеру State. Первый раундовый ключ заполняется на основе секретного ключа, который вы придумаете, по формуле
KeySchedule[r][c] = SecretKey[r + 4c], r = 0,1...4; c = 0,1..Nk.

Понятно, что в KeySchedule мы должны заносить байты, чтобы были возможны дальнейшие операции. Если использовать этот алгоритм для домашнего шифрования, то хранить в голове последовательность чисел совсем не уютно, так что в нашей реализации KeyExpansion() будет на вход брать plaintext строку и применяя ord() для каждого из символов, записывать результат в ячейки KeySchedule. Отсюда вытекают ограничения: не более 16 символов длиной и, так как мы работаем с байтами, ord() символа не должен возвращать значения большие чем 255 или 11111111 в двоичной, иначе получим на выходе неверное шифрование. Получается, что с помощью ключа на русском языке зашифровать не получится.

На рисунке изображен макет KeySchedule для AES-128: 11 блоков по 4 колонки. Для других вариаций алгоритма будет соответственно (Nr + 1) блоков по Nb колонок. Теперь нам предстоит заполнить пустые места. Для преобразований опять определена константная таблица — Rcon — значения которой в шестнадцатеричной системе счисления.

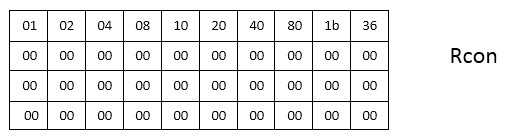
Алгоритм дозаполнения KeySchedule:

• На каждой итерации работаем с колонкой таблицы. Колонки 0,..,(Nk — 1) уже предварительно заполнены значениями из секретного слова. Начинаем с колонки под номером Nk (в нашем случае с четвертой)
• Если номер W_i колонки кратен Nk (в нашем случае каждая четвертая), то берем колонку W_i-1, выполняем над ней циклический сдвиг влево на один элемент, затем все байты колонки заменяем соответствующими из таблицы Sbox, как делали это в SubBytes(). Далее выполняем операцию XOR между колонкой W_i-Nk, измененной W_i-1 и колонкой Rcon_i/Nk-1. Результат записывается в колонку W_i. Чтобы было немного понагляднее, иллюстрация для i = 4.
  
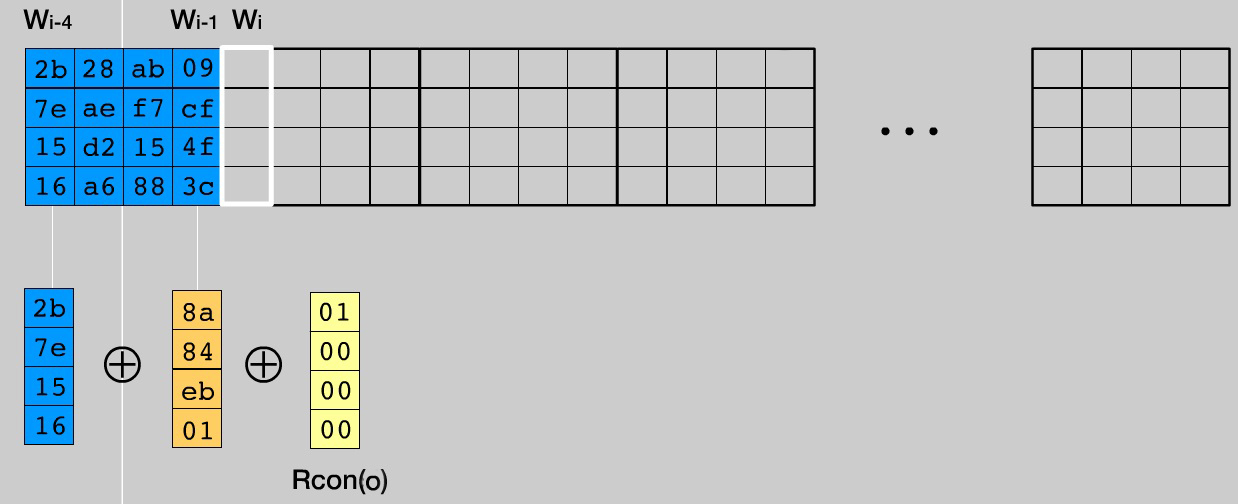
• Для остальных колонок выполняем XOR между W_i-Nk и W_i-1. Результат записываем в W_i

Эта вспомогательная трансформация является самой объемной по написанию и, наверное, самой сложной, после осознания математики в MixColumns(), в алгоритме. Шифроключ обязан состоять из 4*Nk элементов (в нашем случае 16). Но так как мы делаем все это для домашнего применения, то вполне вероятно, что придумывать ключ в 16 символов и запоминать его не каждый будет. Поэтому, если на вход поступила строка длиной менее 16, я в KeySchedule дозаношу значения {01} до нормы.

def key_expansion(key):

    key_symbols = [ord(symbol) for symbol in key]
 
    # ChipherKey shoul contain 16 symbols to fill 4*Nk table. If it's less
    # complement the key with "0x01"
    if len(key_symbols) < 4*nk:
        for i in range(4*nk - len(key_symbols)):
            key_symbols.append(0x01)

    # make ChipherKey(which is base of KeySchedule)
    key_schedule = [[] for i in range(4)]     
    for r in range(4):
        for c in range(nk):
            key_schedule[r].append(key_symbols[r + 4*c])

    # Comtinue to fill KeySchedule
    for col in range(nk, nb*(nr + 1)): # col - column number
        if col % nk == 0:
            # take shifted (col - 1)th column...
            tmp = [key_schedule[row][col-1] for row in range(1, 4)]
            tmp.append(key_schedule[0][col-1])

            # change its elements using Sbox-table like in SubBytes...
            for j in range(len(tmp)):        
                sbox_row = tmp[j] // 0x10
                sbox_col = tmp[j] % 0x10
                sbox_elem =  sbox[16*sbox_row + sbox_col]
                tmp[j] = sbox_elem

            # and finally make XOR of 3 columns
            for row in range(4):
                s = key_schedule[row][col - 4]^tmp[row]^rcon[row][col/nk - 1]
                key_schedule[row].append(s)

        else:
            # just make XOR of 2 columns
            for row in range(4):
                s = key_schedule[row][col - 4]^key_schedule[row][col - 1]
                key_schedule[row].append(s)

    return key_schedule

Как было сказано ранее, KeySchedule используется в трансформации AddRoundKey(). В раунде инициализации раундовым ключом будут колонки с номерами 0,..,3, в первом — с номерами 4,..,7 и тд. Вся суть AddRoundKey() — произвести XOR State и раундового ключа.

Это, собственно, все, что касается процесса шифрования. Выходной массив зашифрованных байтов составляется из State по формуле output[r + 4c] = State[r][c], r = 0,1...4; c = 0,1..Nb. А тем временем статья затягивается, так что мы сейчас быстро пробежимся по процедуре дешифровки.

Быстро о расшифровке

Идея здесь проста: если с тем же ключевым словом выполнить последовательность трансформаций, инверсных трансформациям шифрования, то получится исходное сообщение. Такими инверсными трансформациями являются InvSubBytes(), InvShiftRows(), InvMixColumns() и AddRoundKey(). Общая схема алгоритма расшифровки:

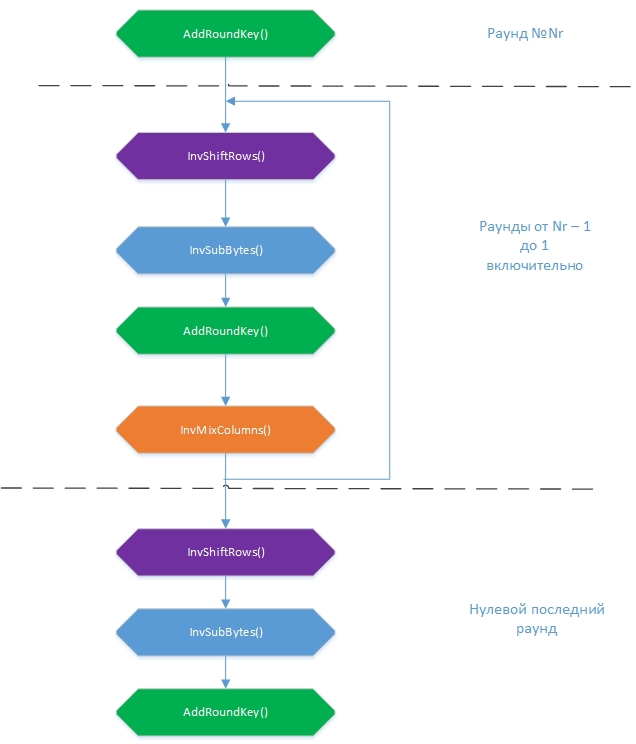
Стоит отметить, что последовательность добавления раундовых ключей в AddRoundKey() должна быть обратной: от Nr + 1 до 0. Изначально, как и при шифровании, из массива входных байтов формируется таблица State. Затем над ней в каждом раунде производятся преобразования, в конце которых должно получиться расшифрованный файл. Порядок трансформаций немного изменился. Что будет первым, InvSubBytes() или InvShiftRows(), на самом деле не важно, потому что одна из них работает со значениями байтов, а вторая переставляет байты, этих самых значений не меняя, но я придерживался последовательности преобразований в псевдокоде стандарта.

InvSubBytes()

Работает точно так же, как и SubBytes(), за исключением того, что замены делаются из константной таблицы InvSbox.

Оставшиеся обратные трансформации тоже будут очень похожи на свои прямые аналоги, поэтому в коде не выделяем под них отдельных функций. Каждая функция, описывающая трансформацию, будет иметь входную переменную inv. Если она равна False, то функция будет работать в обычном или прямом режиме(шифрование), если True — в инверсном(дешифровка).

def sub_bytes(state, inv=False):
  
    if inv == False: # encrypt
        box = sbox
    else:   # decrypt
        box = inv_sbox
    
    for i in range(len(state)):
        for j in range(len(state[i])):
            
            row = state[i][j] // 0x10
            col = state[i][j] % 0x10
            
            # Our Sbox is a flat array, not a bable. So, we use this trich to find elem:
            box_elem = box[16*row + col]
            state[i][j] = box_elem

    return state

InvShiftRows()

Трансформация производит циклический сдвиг вправо на 1 элемент для первой строки State, на 2 для второй и на 3 для третьей. Нулевая строка не поворачивается.

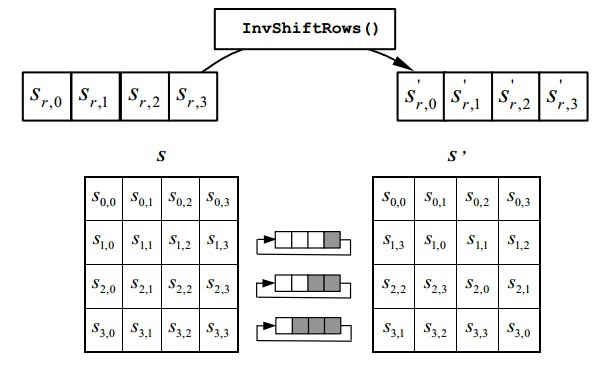
Пояснения к коду: left_shift/right_shift(array, count) поворачивают входной array в соответствующую сторону count раз

def shift_rows(state, inv=False):

    count = 1
    
    if inv == False: # encrypting
        for i in range(1, nb):
            state[i] =  left_shift(state[i], count)
            count += 1
    else: # decryption
        for i in range(1, nb):
            state[i] =  right_shift(state[i], count)
            count += 1

    return state

InvMixColumns()

Операции те же, но каждая колонка State перемножается с другим многочленом {0b}x³ + {0d}x² + {09}x + {0e}. В матричной форме это выглядит так:

Или готовые формулы. Все значения, конечно же, в шестнадцатеричной системе счисления.

Здесь нужно сделать отступление в сторону математики и пояснить как получить функции умножения на константы большие, чем {02}. Как я уже говорил, они получаются путем разложения их через {01} и {02}, а именно:

Разумеется, можно разложить числа и по-другому, но лично проверено, что разложение
n * {09} = n * {03} + n * {03} + n * {03}
и вызов соответствующих функций будут давать неверный результат (эталонные таблицы с результатами есть в одной из ссылок в списке источников).

Пояснения к коду: функции mul_by_<константа> выполняют умножение на соответствующую константу в GF(2⁸) по правилам, что описывались выше.

 def mix_columns(state, inv=False):
  
    for i in range(nb):

        if inv == False: # encryption
            s0 = mul_by_02(state[0][i])^mul_by_03(state[1][i])^state[2][i]^state[3][i]
            s1 = state[0][i]^mul_by_02(state[1][i])^mul_by_03(state[2][i])^state[3][i]
            s2 = state[0][i]^state[1][i]^mul_by_02(state[2][i])^mul_by_03(state[3][i])
            s3 = mul_by_03(state[0][i])^state[1][i]^state[2][i]^mul_by_02(state[3][i])
        else: # decryption
            s0 = mul_by_0e(state[0][i])^mul_by_0b(state[1][i])^mul_by_0d(state[2][i])^mul_by_09(state[3][i])
            s1 = mul_by_09(state[0][i])^mul_by_0e(state[1][i])^mul_by_0b(state[2][i])^mul_by_0d(state[3][i])
            s2 = mul_by_0d(state[0][i])^mul_by_09(state[1][i])^mul_by_0e(state[2][i])^mul_by_0b(state[3][i])
            s3 = mul_by_0b(state[0][i])^mul_by_0d(state[1][i])^mul_by_09(state[2][i])^mul_by_0e(state[3][i])

        state[0][i] = s0
        state[1][i] = s1
        state[2][i] = s2
        state[3][i] = s3
 
    return state

AddRoundKey()

Эта трансформация обратна сама себе в силу свойства операции XOR:

(a XOR b) XOR b = a

Поэтому никаких изменений в нее вносить не нужно. Набор раундовых ключей формируется таким же образом, как и для шифрования с помощью функции KeyExpansion(), но раундовые ключи необходимо подставлять в обратном порядке.

def add_round_key(state, key_schedule, round=0):
        
    for col in range(nk):
        # nb*round is a shift which indicates start of a part of the KeySchedule
        s0 = state[0][col]^key_schedule[0][nb*round + col]
        s1 = state[1][col]^key_schedule[1][nb*round + col]
        s2 = state[2][col]^key_schedule[2][nb*round + col]
        s3 = state[3][col]^key_schedule[3][nb*round + col]

        state[0][col] = s0
        state[1][col] = s1
        state[2][col] = s2
        state[3][col] = s3

    return state

Теперь мы обладаем исчерпывающим набором вспомогательных функций-трансформаций, чтобы написать

def encrypt(input_bytes, key):

    # let's prepare our input data: State array and KeySchedule
    state = [[] for j in range(4)]
    for r in range(4):
        for c in range(nb):
            state[r].append(input_bytes[r + 4*c])

    key_schedule = key_expansion(key)
    
    state = add_round_key(state, key_schedule)

    for rnd in range(1, nr):

        state = sub_bytes(state)
        state = shift_rows(state)
        state = mix_columns(state)
        state = add_round_key(state, key_schedule, rnd)

    state = sub_bytes(state)
    state = shift_rows(state)
    state = add_round_key(state, key_schedule, rnd + 1)

    output = [None for i in range(4*nb)]
    for r in range(4):
        for c in range(nb):
            output[r + 4*c] = state[r][c]

    return output

def decrypt(cipher, key):

    # let's prepare our algorithm enter data: State array and KeySchedule
    state = [[] for i in range(nb)]
    for r in range(4):
        for c in range(nb):
            state[r].append(cipher[r + 4*c])

    key_schedule = key_expansion(key)
    
    state = add_round_key(state, key_schedule, nr)

    rnd = nr - 1
    while rnd >= 1:

        state = shift_rows(state, inv=True)
        state = sub_bytes(state, inv=True)
        state = add_round_key(state, key_schedule, rnd)
        state = mix_columns(state, inv=True)
        
        rnd -= 1

    state = shift_rows(state, inv=True)
    state = sub_bytes(state, inv=True)
    state = add_round_key(state, key_schedule, rnd)

    output = [None for i in range(4*nb)]
    for r in range(4):
        for c in range(nb):
            output[r + 4*c] = state[r][c]

    return output

Эти две функции на вход берут список байтов, не шифрованных или шифрованных, и plaintext строку с секретным ключевым словом.

Заключение, интересные ссылки

Статья получилась довольно длинной. Я старался разбавлять текст картинками и, надеюсь, вам было интересно и никто не заскучал. Код, представленный в статье, не совсем исчерпывающий. Я не вставлял глобальное объявление константных таблиц, мелких функций для MixColumns(), а только на словах пояснил, что они где-то есть. Не сочтите, что я пиарюсь, но полный, склеенный вместе код можно взять в репозитории. Там же лежит скромный CLI интерфейс, который позволяет просто указать путь до файла, ввести секретный ключ и получить зашифрованный файл в той же директории, что и исходный (расшифрованный файл можно получить таким же способом). Шифруйте на здоровье!

И в конце необходимо сказать об одном немаловажном нюансе — padding или дополнение до блока. AES — алгоритм блочного шифрования, функции encrypt()/decrypt() берут на вход ровно один блок входных байтов (для нашего варианта с ключом в 128 бит это 16 байт). В конце файла могут остаться от 1 до 15 байт, которые не формируют цельный блок. Их можно просто, не шифруя, отдать на запись в конечный файл, но в некоторых случаях, в конце файла может содержаться что-то важное, и такой вариант не подходит. Второй вариант мне подсказала статья на Википедии про блочные шифры

Простое дополнение нулевыми битами не решает проблемы, так как получатель не сможет найти конец полезных данных. К тому же, такой вариант приводит к атакам Оракула дополнения. Поэтому на практике применимо решение, стандартизованное как «Метод дополнения 2» в ISO/IEC 9797-1, добавляющее единичный бит в конец сообщения и заполняющее оставшееся место нулями. В этом случае была доказана стойкость к подобным атакам.

Так я и сделал (хотя первый вариант остался, просто закомментированный. Вдруг и пригодится).

Подборка источников:
Официальная документация
Очень наглядная визуальная интерпретация шифрующей части алгоритма. Да не засудит меня автор, сделал оттуда пару скриншотов.
Никуда без Википедии
Отдельная статья про MixColumns(). В ней есть таблицы с результатами умножения списка чисел 0...255 на константы, используемые в шифре, в поле GF(2⁸)
Забавный комикс про историю AES и сам алгоритм. Жалко, что нашел его только тогда, когда уже писал статью.

Автор: Skycker

Источник