Всвязи с наступающим 2014 годом от Рождества Христова может возникнуть вопрос: «А какой же на самом деле сейчас год без привязки к религиям?» На него я постараюсь ответить, а точнее показать, как это можно довольно легко вычислить, не слезая со стула.
Считать будем от момента начала Вселенной, то есть Большого Взрыва. Многие оговорки я буду опускать для получения результата за минимальное количество формул и строчек кода (да-да, мы будем программировать на Питоне!). В качестве бонуса мы также прикинем сколько тёмной энергии у нас во Вселенной.

Supernova 1994D as seen with the Hubble Space Telescope. Foto: Pete Chalis — Harvard Smithsonian Center of Astrophysics
Любопытно? Тогда поехали!
Кратенько о физической стороне вопроса
Слышали про Хаббла? Есть ещё телескоп, названный его именем. Так вот он открыл тот факт, что Вселенная увеличивается в размерах, а точнее что близлежащие к нам галактики разбегаются, и причём чем дальше они от нас, тем быстрее они отдаляются. Как Вселенная может увеличиваться? Аналогия может быть простая. Представьте себя муравьём на воздушном шарике, который надувают. Вам будет казаться, что мир потихоньку увеличивается, и другие муравьи на шарике оказываются всё дальше и дальше, хотя с вашим телом ничего не происходит.
Возвращаясь к Хабблу. Как он этот факт установил? Тут два момента:
- Во-первых, надо измерить скорость галактики. Тут нам понадобится эффект Доплера. Все мы знаем про классический эксперимент со свистом поезда в момент, когда тот проносится вдоль перрона. Когда объект удаляется от нас, то длина волны излучаемая им удлиняется. Из этой поправки можно найти скорость. В астрономии это увеличение называют красным смещением и обозначают буковкой z. Наблюдают какую-нибудь известную спектральную линию и, находя её смещение, вычисляют скорость.
- Во-вторых, расстояние до галактики. Просто так расстояние до них не измерить. Тут нам уже понадобится дополнительный объект — сверхновые типа Ia. Это такие взрывы звёзд, при которых выделяется один и тот же объём энергии. По той яркости, которую мы наблюдаем, можно вычислить расстояние до самого взрыва и до галактики, в которой этот взрыв произошёл. На фото сверху галактика и взрыв сверхновой. По яркости она превосходит всю Галактику, в которой порядка ста миллиардов звёзд.
И где же тут возраст Вселенной?
Замерив с какой скоростью Вселенная увеличивается, мы можем прикинуть, когда она была точкой. Вот этот момент и можно назвать началом всего и прикинуть сколько лет назад он был.
Подготавливаем систему
Нам понадобится Python (версия неважна, я буду использовать 2.7, различия с 3.* минимальны):
sudo apt-get install python
Для вычислений будем использовать Numpy и Scipy:
pip install numpy
pip install scipy
И для графиков Matplotlib:
pip install matplotlib
Для господ без root'а советую такую сборку: store.continuum.io/cshop/anaconda/
Для пользователей Windows: code.google.com/p/pythonxy/
Считаем, что систему подготовили. Всё что идёт дальше можно запускать в интерактивном режиме (прямо в консоли Python), либо в iPython. Кому как нравится.
Скачиваем данные
Прелесть современной астрофизики в полной открытости наблюдательных данных. Мы будем использовать этот каталог сверхновых типа Ia, о которых я писал выше: supernova.lbl.gov/Union/
Нам потребуется этот файл: supernova.lbl.gov/Union/figures/SCPUnion2.1_mu_vs_z.txt
Начинаем писать код
Подключим библиотеки, которые потребуются в последствии.
import numpy as np
import matplotlib.pyplot as plt
Загрузим данные из файла и создадим три вспомогательныъ массива:
# пропускаем 5 строчек заголовка, в котором написано что в каком столбце записано.
# пропускаем 0ой столбец, формат которого сложно распознать, и в котором буквенный идентификатор сверхновой
data=np.loadtxt('SCPUnion2.1_mu_vs_z.txt',skiprows=5,converters={0: lambda s: 0})
# создаём массив с красными смещениями из второго столбца
z = data[:,1]
# создаём массив с distance modulus из третьего столбца и ошибки из четвёртого
DM = data[:,2]
DM_err=data[:,3]
О том, что такое Distance modulus и как из него получить расстояние до объекта, лаконично написано на белоруской Википедии.
Сконвертируем эту величину, существование которой вызвано исключительно удобством наблюдателей, в физическую. Расстояние до объектоа запишем в массив DL:
# определяем функцию конвертации
def DM2DL(DM):
return 10**(DM/5-1)/1e4
# конвертируем сразу весь массив
DL=DM2DL(DM)
При подсчёте Distance Modulus авторы каталога предположили, что светимость сверхновой -19.3, о чём написано в описании. Эту работу они сделали за нас.
Теперь в переменной z у нас записаны красные смещения и в DL — расстояния в Мегапарсеках (1 парсек = 3e16 метров = 3,3 световых года). Можно построить рисунок и посмотреть, что получилось:
plt.plot(DL,z,'.')
plt.xlabel(r'$D_{L};mathrm{[Mpc]}$',size=18)
plt.ylabel(r'$z$',size=18)
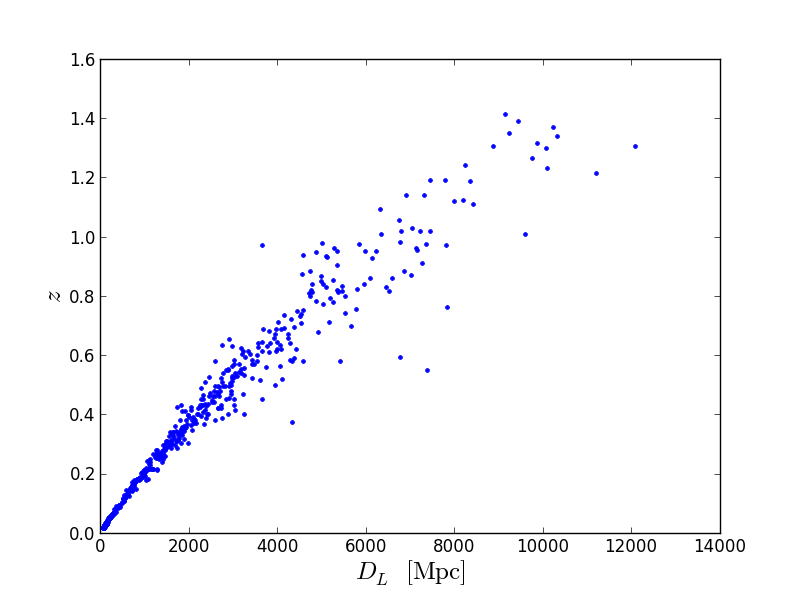
Теперь давайте сконвертируем красное смещение, z, в скорость. Для начала нам потребуется функция для конвертации скорости в красное смещение, то есть обратная функция:
# конвертируем скорость в красное смещение и наоборот
# скорость света
c=29979245800 # cm/s
# функция конвертации скорости в красное смещение
def v2z(v):
return sqrt((1.0+v/c)/(1.0-v/c))-1.0
Формула взята отсюда: en.wikipedia.org/wiki/Redshift#Redshift_formulae
Для конвертации в обратную сторону мы заранее посчитаем соответствие между z_list и v_list, после чего напишем функцию, которая интерполирует между точками:
v_list=linspace(0,c,100)
z_list=v2z(v_list)
# plt.plot(z_list,v_list)
def z2v(z):
return np.interp(z,z_list,v_list)/1e5
v=z2v(z) # km/s
Посмотрим на скорость объекта в зависимости от его расстояния от нас:
plt.plot(DL,v,'.')
plt.xlabel(r'$D_{L};mathrm{[Mpc]}$',size=18)
plt.ylabel(r'$v;mathrm{[km/s]}$',size=18)
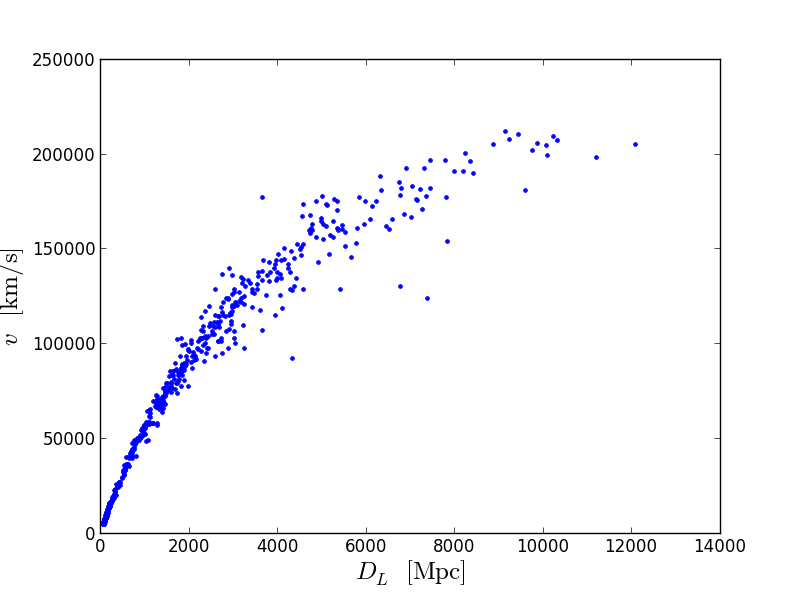
На этой картинке отчётливо видно, что чем дальше объект, тем быстрее он от нас удаляется. Попробуем профитировать прямую. Наклон прямой (производная) в точке 0 называется постоянной Хаббла, H, и измеряется в км/c/Мпс. Можно найти этот наклон путём фитирования, но мы пойдём простым путём. Просто подберём наклон:
plt.plot(DL,v,'.')
plt.xlabel(r'$D_{L};mathrm{[Mpc]}$',size=18)
plt.ylabel(r'$v;mathrm{[km/s]}$',size=18)
temp=np.array([0.0,20.0])
plt.plot(temp,50.0*temp,'r')
plt.plot(temp,70.0*temp,'g')
plt.plot(temp,100.0*temp,'m')
plt.legend(('data','H=50','H=70','H=100'))
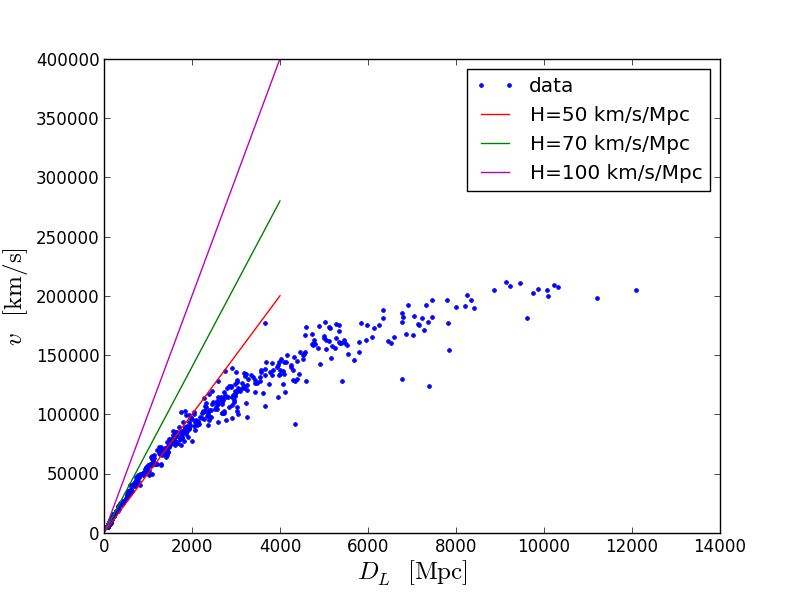
И увеличенная версия:
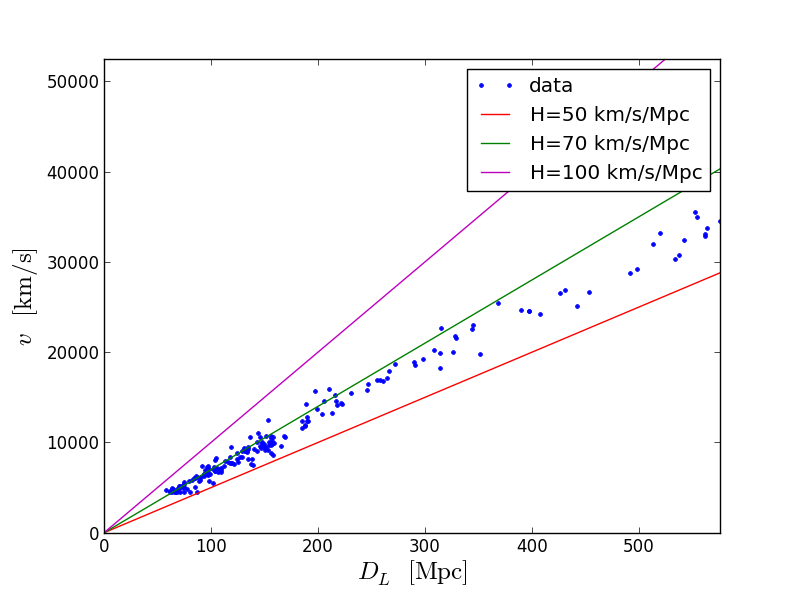
Самая точная догадка: H=70 км/с/Мпс. То есть объект находящийся в 1 Мпс от нас удаляется со скоростью 70 км/с. Другими словами мы с ним были в одной точке столько лет тому назад (предполагая, что скорость разбегания была постоянной):
(1 Мпс) / (70 км/с) = 1 / H = 14 000 000 000 лет назад
(Гугл хорошо справляется с конвертацией различных единиц измерения.)
Итого, спустя несколько строчек кода мы установили, что возраст Вселенной порядка 14 миллиардов лет. Во-первых, это очень грубая оценка. Во-вторых, мы не оценили ошибку измерений, что необходимо делать при любом эксперименте. Также мы не говорили, откуда мы знаем яркость взрывов сверхновых, и почему мы считаем их одинаковыми. Это всё тоже отдельные интересные темы. Тем не менее такая грубая оценка даёт неплохой результат! Более точный анализ со всеми известными наблюдениями даёт результат в 13.813±0.058 миллиардов лет.
Хаббл же в своё время наблюдал только самое начало подобной диаграммы (из его статьи 1929 года apod.nasa.gov/diamond_jubilee/d_1996/hub_1929.html )
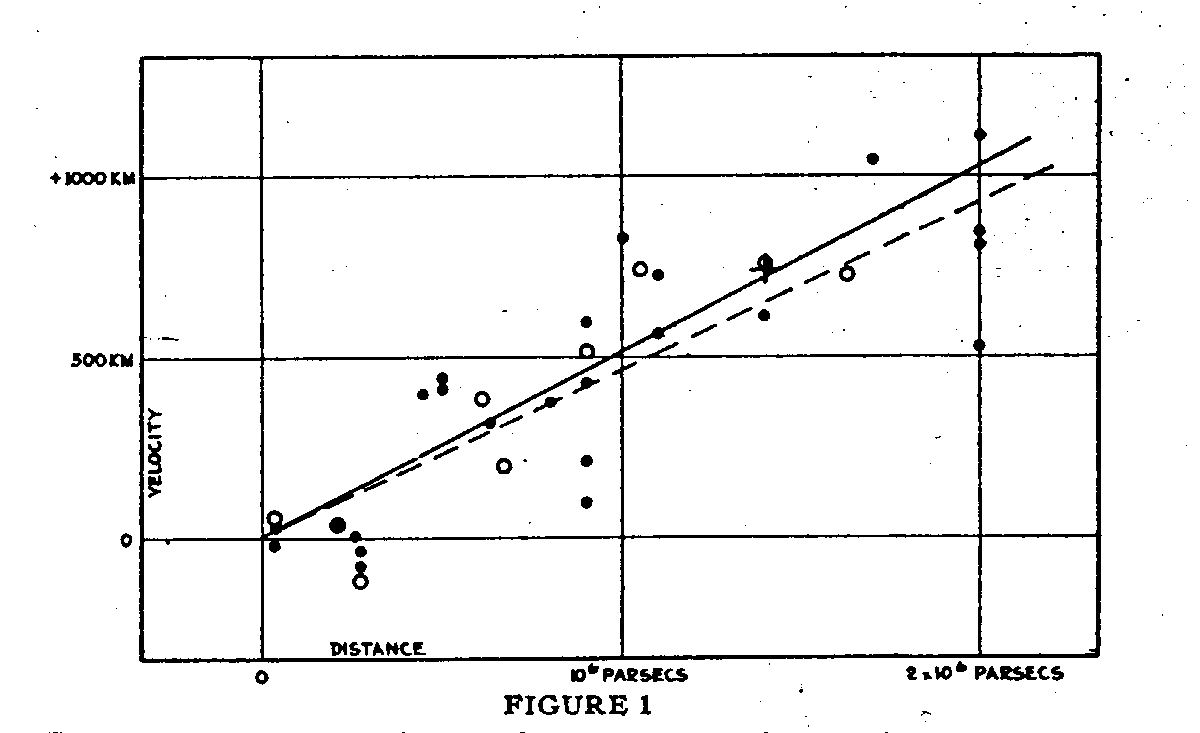
и получил вместо 70, число 500. Тем не ошибка меньше чем в 10 раз, что защитывается за попадание.
Тёмная энергия?
На рисунках можно заметить, что линия вписывается только вначале диаграммы. Далее же линейное приближение совсем не подходит. Для следующего шага нам надо будет немного погрузиться в космологию. В самой простой модели Вселенная состоит из материи и из тёмной энергии (Эйнштейновского лямбда члена), и при этом является плоской. Обозначив часть Вселенной, состоящей из материи, за Omega_M и другую часть Вселенной из некой тёмной энергии за Omega_L, причём Omega_M+Omega_L=1, я могу выразить расстояние до объекта через красное смещение с помощью формулы (подробнее можно почитать на Википедии: [1] [2]):
Вводим вспомагательную функцию E(z):
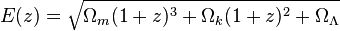
Omega_k, которая здесь фигурирует, отвечает за кривизну Вселенной. Для простоты считаем её плоской, то есть Omega_k=0. Поэтому в следующей формуле нам нужна средняя строчка:
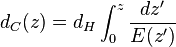
Ключевой интеграл
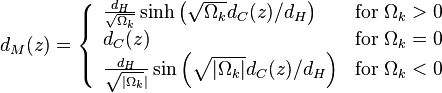
Дополнительный множитель (1+z), происхождение которого слишком долго объяснять :) :
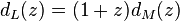
Далее напишем код, который вычисляет интеграл:
# функция E_z
def e_Z(z, OmegaM):
OmegaL=1.0-OmegaM
return (OmegaM*(1.0+z)**3+OmegaL)**(-0.5)
# подключаем модуль scipy для интегрирования
import scipy.integrate as si
# расстояние
def D_L(z, OmegaM):
dh=4286.0 # это величина c/H, где H мы считаем равным 70 км/с/Мпс
D_c=dh*si.quad(e_Z,0.0,z,args=(OmegaM))[0]
return D_c*(1.0+z)
# делаем обёртку предыдущей функции, чтобя она работала сразу с массивами
def D_L_batch(z,OmegaM,H):
DL=z.copy()
for i in range(len(z)):
DL[i]=D_L(z[i],OmegaM,H)
return DL
# делаем рисунок
plt.plot(DL,v,'.')
plt.xlabel(r'$D_{L};mathrm{[Mpc]}$',size=18)
plt.ylabel(r'$v;mathrm{[km/s]}$',size=18)
# временная переменная с координатами в z-пространстве от 0 до 1.5, 100 точек
temp_z=np.linspace(0,1.5,100)
# временная переменная с соответствующими координатами в v-пространстве
temp_v=z2v(temp_z)
# добавляем на рисунок три модели с разными величинами Omega_M
plt.plot(D_L_batch(temp_z,0.01,70.0),temp_v,'r')
plt.plot(D_L_batch(temp_z,0.27,70.0),temp_v,'g')
plt.plot(D_L_batch(temp_z,0.99,70.0),temp_v,'m')
plt.legend(('data',r'$Omega_M=0.01$',r'$Omega_M=0.27$',r'$Omega_M=0.99$'),loc=4)
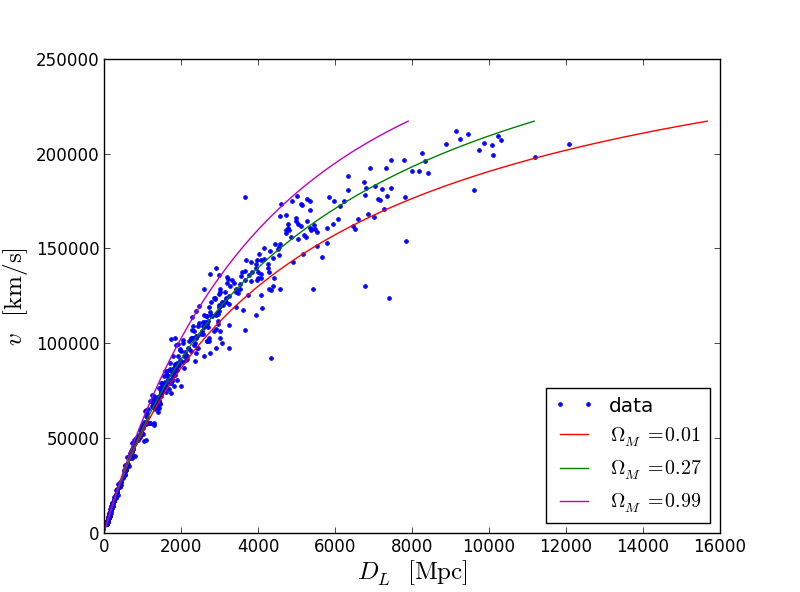
Зелёная кривая подходит к данным чуть лучше. Про ошибку вписывания теории в данные мы опять же для простоты забываем. Вывод следующий. Количество тёмной энергии и материи сопоставимы сегодня (модели, в которых отношение 100 к 1 в данные не вписываются). Это довольно интересный факт. Порядка ~70% Вселенной — некая тёмная энергия, природу которой мы пока не понимаем. Оставшиеся ~30% материи тоже не так просты как кажутся. Из неё только пятая часть является барионной материи (та из которой мы состоим), а остальное — тёмная материя. Что касается неё, то её количество тоже можно оценить как-нибудь в другой раз.
Ну вот мы и закончили. На последок лишь скажу, что это далеко не единственный способ измерения геометрии и возраста Вселенной. Их несколько. И что примечательно, все они говорят в пользу теории Большого Взрыва и расширяющейся Вселенной.
Удачного празднования именин Иисуса, господа! :)
Автор: akaurov





