Введение
Карл Давид Тольме Рунге (30 августа 1856 - 3 января 1927) - выдающийся немецкий математик, физик и спектроскопист. Обучался в Берлинском университете, где получил степень PhD, являлся профессором математики в Ганноверском университете, а также главой кафедры прикладной математики в Гёттингене. [1]
в 1901 году Карл открыл "Феномен Рунге" - в численном анализе эффект нежелательных колебаний, возникающий при интерполяции полиномами высоких степеней - о котором пойдёт речь в данной статье. [2]
Но прежде, чем мы окунёмся глубже в изучение данного феномена, давайте поговорим об интерполяционном многочлене Лагранжа, на примере которого мы и разберём Феномен Рунге.
Интерполяционный многочлен Лагранжа
Полином Лагранжа - это математическая функция, позволяющая записать полином n-степени, который будет соединять все заданные точки из набора значений, полученных опытным путём или методом случайной выборки. Многочлен в форме Лагранжа в явном виде содержит значения функций в узлах интерполяции, поэтому он удобен, когда значения функций меняются, а узлы интерполяции неизменны. Число арифметических операции, необходимых для построения многочлена Лагранжа, пропорционально и является наименьшим для всех форм записи. [3]
Полином Лагранжа в общем виде выглядит следующим образом:
где - это базисные полиномы Лагранжа, определяющиеся как
где
Так, например, интерполяционный многочлен в форме Лагранжа, проходящий через три заданных точки будет записываться вот так: [3]
Погрешность интерполяционного многочлена Лагранжа описывается следующим образом:
Пример полинома Лагранжа
Для лучшего понимания составления полинома Лагранжа, давайте рассмотрим простенький пример. Мы выберем три точки
Начнём с составления базисных полиномов Лагранжа:
Таким образом, полином Лагранжа выглядит вот так:
Демонстрация феномена Рунге через полином Лагранжа
Мы хотим аппроксимировать функцию на
интервале используя полином Лагранжа.
Используя функцию интерполяции Лагранжа SciPy, мы вычислим полином Лагранжа степени .
Здесь мы рассматриваем узлы для
Мы построим графики различных полиномов и функции на интервале
import numpy as np
from scipy.interpolate import lagrange
import matplotlib.pyplot as plt
def f(x):
return 1/(1+25*x**2)
n=100
x_fine=np.linspace(-1, 1, 1000)
y_fine=f(x_fine)
plt.plot(x_fine, y_fine, color='black', label='f(x)')
for degree in range(6,13,2):
x_nodes=np.array([-1+(2*i/degree)for i in range(degree+1)])
p_n=lagrange(x_nodes, f(x_nodes))
y_nodes=p_n(x_fine)
plt.plot(x_fine, y_nodes, label=f'Полином Лагранжа Степени {degree}')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()
plt.show()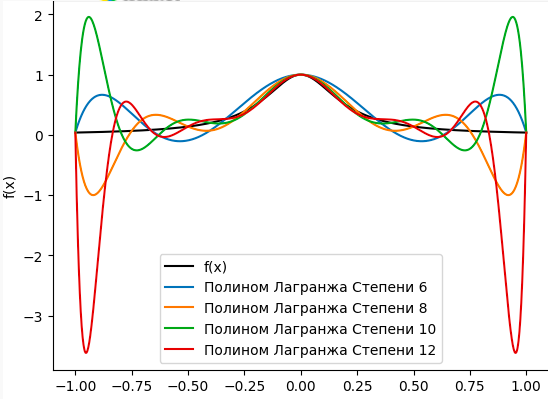
На графике наглядно продемонстрирован Феномен Рунге - интерполирующий полином сильно колеблется на крайних точках интервала, причем большая степень полинома гарантирует большие колебания.
Феномен Рунге показывает, что переход к более высоким степеням не всегда повышает точность. Почему такое происходит? Давайте обратимся к погрешности Лагранжа.
Для случая функции Рунге, интерполированной в равноудаленных точках, каждый из двух множителей в погрешности аппроксимации растет до бесконечности с ростом n. Хотя это часто используется для объяснения феномена Рунге, тот факт, что верхняя граница погрешности стремится к бесконечности, не обязательно подразумевает, конечно, что сама погрешность также расходится с n. [4]
Решение проблемы
Одним из эффективных способов решить проблему и избежать феномена Рунге, является использование узлов Чебышёва. В математике под узлами Чебышёва понимают корни многочлена Чебышёва первого рода. Их отличительная черта заключается в том, что они распределены не равномерно, а сконцентрированы ближе к крайним точкам интервала.
Для натурального числа n узлы Чебышёва на отрезке задаются формулой: [5]
import numpy as np
from scipy.interpolate import lagrange
import matplotlib.pyplot as plt
def f(x):
return 1/(1+25*x**2)
def chebyshev_nodes(n):
nodes=np.zeros(n+1)
for i in range (n+1):
nodes[i]=np.array(np.cos((2*i+1)*np.pi/(2*(n+1))))
return nodes
n=100
x_fine=np.linspace(-1, 1, 1000)
y_fine=f(x_fine)
plt.plot(x_fine, y_fine, color='black', label='f(x)')
for degree in range(6,13,2):
x_nodes=np.array(chebyshev_nodes(degree))
p_n=lagrange(x_nodes, f(x_nodes))
y_nodes=p_n(x_fine)
plt.plot(x_fine, y_nodes, label=f'Лаг Пол Ст {degree}')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend(loc='upper left')
plt.show()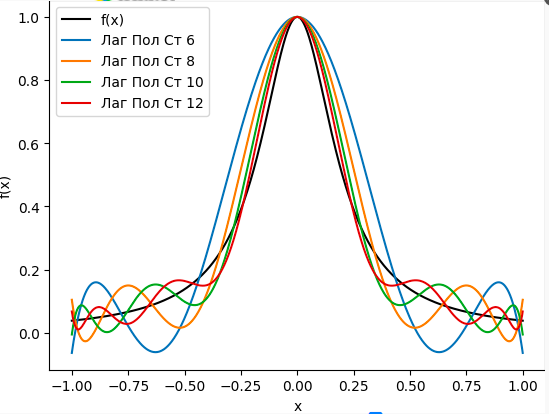
Как мы видим по графику, интерполяция на узлах Чебышёва значительно уменьшает колебания в крайних точках, то есть улучшает аппроксимацию.
Заключение
Феномен Рунге подчеркивает ограничения интерполяции на равномерно распределенных узлах, показывая увеличение погрешности на крайних точках интервала интерполяции до бесконечности. Но, к нашему счастью, решение проблемы существует, стоит всего лишь обратиться к узлам Чебышёва.
Список Литературы
-
https://dic.academic.ru/dic.nsf/ruwiki/491639
-
https://ru.wikipedia.org/wiki/Феномен_Рунге
-
http://simenergy.ru/mathematical-analysis/basic-data/lagrange-polynomial
-
http://www.tlu.ee/~tonu/Arvmeet/Runge's%20phenomenon.pdf
-
https://en.wikipedia.org/wiki/Chebyshev_nodes
Автор: kristina_ponomareva









