Введение
Еще в 1940-х годах, Джон фон Нейман и Станислав Улам изобрели моделирование Монте-Карло или численный метод Монте-Карло. Они назвали его в честь известного места азартных игр в Монако, поскольку этот метод имеет те же случайные характеристики, что и игра в рулетку.
Методы Монте-Карло представляют собой широкий класс вычислительных алгоритмов, которые полагаются на повторяющуюся случайную выборку для получения численных результатов. Основная концепция заключается в использовании случайности для решения проблем, которые в принципе могут быть детерминированными. Численный метод Монте-Карло использует три класса задач, такие как оптимизация, численное интегрирование и генерация результатов на основе распределения вероятностей.
Метод Монте-Карло используется в реальной жизни, например, в задачах, связанных с физикой, создании искусственного интеллекта, прогнозировании погоды и так далее, а также имеет огромное применение в финансах, где числовой метод Монте-Карло используется для расчёта стоимости акций, прогнозировании продаж, управления проектами и многого другого. [1]
Основное преимущество использования Монте-Карло заключается в том, что этот метод обеспечивает множество возможных результатов и вероятность каждого из большого пула случайных выборок данных, однако, метод зависит от предположений, и это иногда может быть сложной задачей. Некоторые другие преимущества Монте-Карло: он изучает поведение системы без её построения, обеспечивает в целом точные результаты, по сравнению с аналитическими моделями, помогает обнаружить неожиданное явление и поведение системы, а также выполнить анализ "что, если". [2]
В этой статье метод Монте-Карло будет использоваться для аппроксимации как одномерных, так и многомерных интегралов.
Описание Метода
Как известно, чтобы вычислить. интеграл по графику, нам нужно вычислить площадь под кривой. Давайте рассмотрим график функции, который выглядит как 1/4 круга с радиусом, равным единице. Его площадь равна π * радиус2. Теперь, эту часть круга, мы поместим в квадрат со стороной, равной единице, и, соответственно, площадью равной единице. Используя эту информацию, мы можем вычислить площадь круга, которая будет равна π * радиус2/4 = π/4 = 0,785.
Теперь давайте выберем несколько точек на нашем графике, которые находятся внутри квадрата. Примечание: они не должны быть внутри круга, просто, внутри квадрата. Допустим, мы использовали 18 разных точек, где 14 из них находятся внутри круга, а другие 4 - только внутри квадрата. Примечание: поскольку круг занимает значительную часть квадрата, логично, что количество точек в круге будет больше, чем количество точек вне его. Теперь, чтобы вычислить площадь круг, нам нужно разделить количество точек внутри круга (14) на общее количество точек (18). Площадь круга = 14/18 = 0,77777778, что примерно равно 0,785. Этот метод аппроксимации интеграла называется Монте-Карло, и его формула: [3], [4]
Давайте упомянем, что точки, которые мы берём - случайны, поэтому, если мы используем ту же кривую для вычисления её площади, мы можем получить немного другой результат. И, как мы можем подвести итог, большее количество точек даст нам более точный результат.
Но что, если нам нужно аппроксимировать многомерный интеграл? Что, если форма нашей функции не такая простая? Допустим, нам нужно вычислить объём сферы. Мы можем сделать это, вычислив тройной интеграл:
Мы собираемся интегрировать, используя метод Монте-Карло.
Первым шагом будет выбор N - количества случайных точек для генерации и r - радиуса сферы. Следующим шагом будет генерация точек, значений для ri, θi, φi относительно пределов интеграла, поэтому 0≤ri≤r, 0≤θi≤π, 0≤фi≤2π.
Для каждой случайной точки ri, θi, фi, мы оценим подынтегральное выражение f (ri,θi, фi) = ri2 * sin(θi) и после этого вычислим среднее значение подынтегрального выражения, суммируя все значения, которые мы получили на предыдущем шаге, деленные на N.
Теперь мы готовы к нашему последнему шагу, где мы вычисляем объём сферы. Умножим окончательный результат из предыдущей части на трехмерный объём, который можно вычислить как Объём = (bx - ax) * (by - ay) * (bz - az) = (r - 0) * (π - 0) * (2π - 0). Объём приближения =
является окончательным приближением тройного интеграла для объёма сферы с использованием численного метода Монте-Карло. [5]
Теория и Погрешность Метода
Интеграция Монте-Карло для одномерного интеграла:
Где xi — случайно равномерно распределенные точки внутри [a,b], а N — количество этих точек.
Из этого уравнения мы видим, что 
представляет собой просто среднее значение функции, а это означает, что мы можем быть уверены только в оценке в пределах стандартного отклонения средней оценки.

— оценка стандартного
отклонения функции, как . Итак, это означает,
что погрешность зависит от и уменьшается по мере того, как
стремится к 0, поэтому, увеличивая N, мы уменьшаем
погрешность. Подводя итог, можно сказать, что погрешность аппроксимации с небольшим количеством точек может быть большой и аппроксимация даст недостаточно точные результаты, что делает метод Монте-Карло менее эффективным, чем другие, например, чем правило Симпсона.
Давайте рассмотрим одномерный простой интеграл:
Вычисляя его вручную, получаем
Теперь давайте вычислим его с помощью численного интегрирования Симпсона. Степень точности по правилу Симпсона равна 3, что означает, что приближение данного интеграла будет иметь погрешность.
Формула правила Симпсона
Для нашего интеграла с использованием Симпсона имеем:
.
Число операций для правила Симпсона здесь равно 9.
Теперь давайте аппроксимируем тот же интеграл с помощью Монте-Карло. Мы выберем 3 случайные равномерно распределенные точки на интервале [0, 1]. Скажем, .
.
Количество операций здесь также равно 9. Как мы знаем, Монте-Карло становится точнее с ростом , однако мы видим, что количество операций также увеличится. Например, для
у нас будет 12 операций вместо 9.
Абсолютная погрешность при использовании правила Симпсона составляет , а при использовании Монте-Карло —
. Количество используемых операций одинаково, поэтому очевидно, что правило Симпсона даёт лучшее приближение.
Итак, для одиночного интеграла, Монте-Карло — не лучший метод, но как насчет многомерных интегралов?
Интеграция Монте-Карло для пространства D:
Где — это D-мерный объем, xi — случайно и равномерно распределенные точки в объеме
.
Здесь можно отметить, что .
— это оценка стандартного отклонения функции,
так как . Таким образом, это означает, что погрешность по-прежнему
зависит от , как в приближении одиночного интеграла.
Количество операций, а также погрешность остаются такими же, как и при приближении одиночного интеграла. Для ряда операций нам все еще нужно сгенерировать точек,
выполнить оценок функций, выполнить
суммирований, выполнить вычисление
, деление
и
и умножение
и
.
Что делает метод Монте-Карло намного лучше других для многомерных интегралов, так это то, что в других методах время оценки увеличивается со скоростью , это происходит из-за разбиения областей интегрирования. Например, интеграл:
для правила Симпсона будет разделен как
И если мы продолжим разбивать область интегрирования на точек в каждом из
измерений, то количество оценок, а значит и время расчета, возрастет на
. Для Монте-Карло количество вычислений останется прежним, и, следовательно, время расчета останется таким же, как для одиночного интеграла.
Подводя итог, для многомерных интегралов Монте-Карло является полезным методом, который доминирует над другими методами. [4]
Оригинальный Код
import numpy as np
N=1000 #Количество точек для случайной выборки
approximations = np.zeros(N)
def f(x, y, z): #определить функцию для интегрирования (здесь функция в интеграле для расчета объёма сферы)
return 1
def random_points(a_x, b_x, a_y, b_y, a_z, b_z): #Определить функцию для генерации случайных точек
r=np.random.uniform(a_x, b_x) #Сгенерировать случайные значения радиуса
theta=np.random.uniform(a_y, b_y) #Сгенерировать случайные значения угла тэта
phi=np.random.uniform(a_z, b_z) #Сгенерировать случайные значения угла фи
return r, theta, phi
def spherical_coordinates(r, theta, phi): #Определить функцию для конвертации в сферические координаты
x=r*np.sin(theta)*np.cos(phi)
y=r*np.sin(theta)*np.sin(phi)
z=r*np.cos(theta)
return x, y, z
for i in range (N):
r, theta, phi = random_points(0, 5, 0, np.pi, 0, 2*np.pi)
x, y, z = spherical_coordinates(r, theta, phi)
dV=r**2*np.sin(theta) #Оставшийся компонент от dV=r**2*sin(theta) dr dtheta dphi"
approximations[i]=f(x, y, z)*dV #Вычислить подынтегральную функцию
Monte_Carlo_Approximation=(np.sum(approximations)/N)*(5-0)*(np.pi-0)*(2*np.pi-0)
print ("Объём сферы подсчитанный с помощью метода Монте-Карло =", Monte_Carlo_Approximation) 
Применение
Мы будем вычислять тройной интеграл:
где E – половина сферы, y≥0 и x2+y2+z2=4
Сначала мы определим нашу функцию f (x, y, z) = x2 + y2.
Из описания задачи мы видим, что радиус сферы равен 2, так как в сферических координатах x2 + y2 + z2 = r2, значит, r = 2. Поэтому, мы собираемся изменить наш оригинальный код и сгенерировать случайные значения для r от 0 до 2. Затем, поскольку мы работаем только с половиной сферы, которая находится там, где y ≥ 0, наше значение φ будет 0 ≤ φ ≤ π. Для θ значение по-прежнему 0 ≤ θ ≤ π.
Затем мы преобразуем наши координаты x, y, z в сферические координаты, где
x = r ∗ sin θ cos φ
y = r ∗ sin θ sin φ
z = r ∗ cos θ
dV = r2 ∗ sin θ dr dθ dφ
Мы оценим подынтегральные функции f (ri, θi, φi) = ((ri ∗ sin θi ∗ cos φi)2 + (ri ∗ sin θi ∗ sin φi)2) ∗ r2i ∗ sin(θi), а затем вычислим приближение интеграла с помощью численного метода Монте-Карло.
Приближение =
Мы также вычислим интеграл вручную и получим точный результат, который равен 128π/15 ≈ 26,8082573106.
В коде, мы выведем значение приближения, а также абсолютную погрешность
import numpy as np
N=1000
approximations=np.zeros(N)
Monte_Carlo_Approximation=[]
def f(x, y, z):
return x**2+y**2
for i in range (N):
r=np.random.uniform(0, 2)
theta=np.random.uniform(0, np.pi)
phi=np.random.uniform(0, np.pi)
x=r*np.sin(theta)*np.cos(phi)
y=r*np.sin(theta)*np.sin(phi)
z=r*np.cos(theta)
dV=r**2*np.sin(theta)
approximations[i]=f(x, y, z)*dV
Monte_Carlo_Approximation.append(np.sum(approximations)/(i+1)*(2-0)*(np.pi-0)*(np.pi-0))
absolute_error=abs(Monte_Carlo_Approximation[N-1]-(128*np.pi)/15)
print("Интеграл, вычисленный с помощью метода Монте-Карло =", Monte_Carlo_Approximation[N-1])
print("Абсолютная погрешность =", absolute_error)
Проверка
В первом тесте мы проверим, что погрешность в интегрировании Монте-Карло для
одиночных интегралов зависит от , что означает, что, увеличивая
, мы будем
приближаться все ближе и ближе к фактическому результату, поэтому абсолютная погрешность будет уменьшаться.
Дробь означает
, поэтому мы построим линию
салатового цвета.
Интеграл для примера возьмём .
Теперь давайте вычислим приближения интеграла с помощью Монте-Карло и вычислим абсолютную погрешность. Мы сделаем 9 различных приближений, первое будет с 50 точками, второе с 100 и так далее до 50000. Мы также запустим аппроксимацию с каждым количеством точек по 30 раз и вычислим среднюю абсолютную погрешность. Поскольку интегрирование Монте-Карло зависит от случайно сгенерированных точек, иногда поведение абсолютной погрешности может зависеть от «лучших» или «худших» сгенерированных точек, поэтому мы хотим убедиться, что мы запускаем код для аппроксимации для каждого количества точек несколько раз, а затем строим график среднего значения.
Средняя абсолютная погрешность для точек в 50, 100, 500, 1000, 2000, 2500, 5000, 10000, 50000 будет отображена розовым цветом.
Как мы видим, салатовая и розовая линии кажутся параллельными (опять же, они не идеально параллельны, поскольку Монте-Карло зависит от случайно сгенерированных точек).
Итак, анализируя график, можно сделать вывод, что численный метод интегрирования
Монте-Карло для одиночных интегралов имеет скорость сходимости .
import numpy as np
import matplotlib.pyplot as plt
nb_N=9
N_val = np.array([50, 100, 500, 1000, 2000, 2500, 5000, 10000, 50000])
approximations=np.zeros(nb_N)
nb_sample = 30
error=np.zeros((nb_N, nb_sample))
average_error = np.zeros(nb_N)
def f(x):
return x**5
Monte_Carlo_Approximation= np.zeros(nb_N)
for i in range (nb_N):
for j in range (nb_sample):
x=np.random.uniform(0, 1, N_val[i])
approximations=f(x)
Monte_Carlo_Approximation[i]=((np.sum(approximations)/(N_val[i]))*(1-0))
absolute_error=np.abs(Monte_Carlo_Approximation[i]-(1/6))
error[i, j]=absolute_error
average_error[i]=np.mean(error[i])
plt.loglog(N_val, average_error, color='deeppink', marker='o', label='Абсолютная Погрешность')
plt.loglog(N_val, N_val**(-1/2), color='lime', label='N^(-1/2)')
plt.xlabel("Количество Точек")
plt.ylabel("Абсолютная Погрешность")
plt.title('График Сходимости')
plt.legend()
plt.show()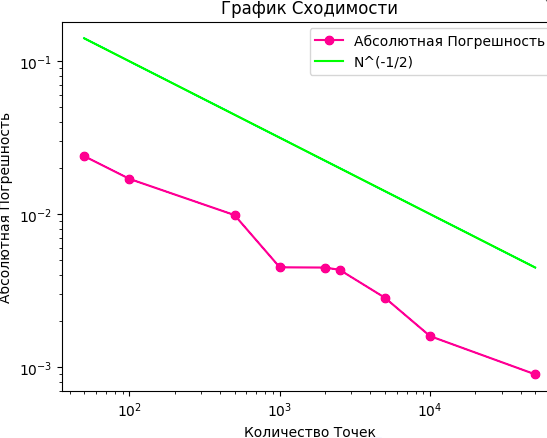
Теперь, чтобы убедиться, что погрешность имеет одинаковую скорость сходимости как для многомерных, так и для одиночных интегралов в приближении Монте-Карло, мы построим график сходимости для многомерного интеграла.
Рассматриваемый интеграл — , где
— это вся сфера с радиусом
Мы выполним приближение Монте-Карло для 9 различных количеств точек, 50, 100, 500, 1000, 2000, 2500, 5000, 10000, 50000. И для каждого набора точек мы запустим приближение 30 раз, вычислим 30 абсолютных погрешностей, а затем построим среднюю абсолютную погрешность для каждого из этих наборов.
Поскольку мы пытаемся доказать, что скорость сходимости , мы нарисуем
линию голубым цветом, а среднюю абсолютную погрешность — оранжевым.
Как мы видим, голубая и оранжевая линии кажутся параллельными (опять же, они не идеально параллельны, поскольку Монте-Карло зависит от случайно сгенерированных точек). Таким образом, анализируя график, мы можем подвести итог, что численный метод интегрирования Монте-Карло как для одномерных, так и для многомерных
интегралов имеет скорость сходимости
import numpy as np
import matplotlib.pyplot as plt
nb_N=9
N_val = np.array([50, 100, 500, 1000, 2000, 2500, 5000, 10000, 50000])
nb_sample = 30
error=np.zeros((nb_N, nb_sample))
approximations=np.zeros(nb_N)
average_error = np.zeros(nb_N)
Monte_Carlo_Approximation= np.zeros(nb_N)
def f(x, y, z):
return x**3*y**2*z
def random_points_N(a_x, b_x, a_y, b_y, a_z, b_z, N):
r=np.random.uniform(a_x, b_x, N)
theta=np.random.uniform(a_y, b_y, N)
phi=np.random.uniform(a_z, b_z, N)
return r, theta, phi
def random_points(a_x, b_x, a_y, b_y, a_z, b_z):
r=np.random.uniform(a_x, b_x)
theta=np.random.uniform(a_y, b_y)
phi=np.random.uniform(a_z, b_z)
return r, theta, phi
def spherical_coordinates(r, theta, phi):
x=r*np.sin(theta)*np.cos(phi)
y=r*np.sin(theta)*np.sin(phi)
z=r*np.cos(theta)
return x, y, z
for i in range (nb_N):
for j in range (nb_sample):
r, theta, phi = random_points_N(0, 5, 0, np.pi, 0, 2*np.pi, N_val[i])
x, y, z = spherical_coordinates(r, theta, phi)
dV=r**2*np.sin(theta)
approximations=f(x, y, z)*dV
Monte_Carlo_Approximation[i]=((np.sum(approximations)/(N_val[i]))*(5-0)*(np.pi-0)*(2*np.pi-0))
absolute_error=np.abs(Monte_Carlo_Approximation[i]-((500*np.pi)/3))
error[i, j]=absolute_error
average_error[i]=np.mean(error[i])
plt.loglog(N_val, average_error, color='orangered', marker='o', label='Абсолютная Погрешность')
plt.loglog(N_val, 10e3*N_val**(-1/2), color='cyan', label='N^(-1/2)')
plt.xlabel("Количество Точек")
plt.ylabel("Абсолютная Погрешность")
plt.title('График Сходимости')
plt.legend()
plt.show()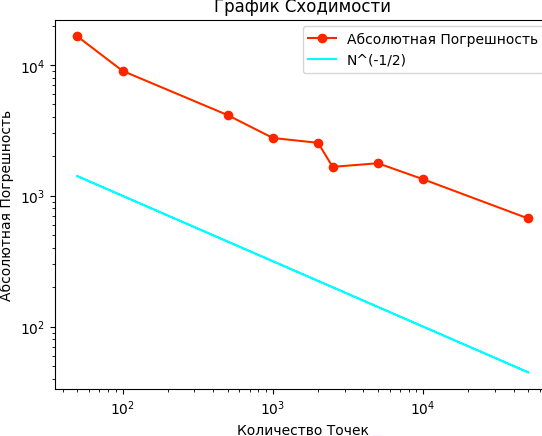
Заключение
Метод Монте-Карло является действенным методом для вычисления многомерных интегралов. Он лёгок в применении, а также, его погрешность может быть уменьшена за счёт увеличения количества выборки.
Как и у любого метода, у Монте-Карло есть свои минусы. Например, при работе с маленьким количеством информации, дисперсия слишком высока, и в таких случаях, лучше обратиться к другим методам.
Список Литературы
-
https://en.wikipedia.org/wiki/Monte_Carlo_method
-
What is Monte Carlo Simulation? by Amazon Web Service
-
Evaluating the Area of a Circle and the Volume of a Sphere by Using Monte Carlo Simulation by Iraqi Journal of Statistical Science (14) 2008 (p.p. [48-62])
-
William&Mary College Physics Textbook Chapter 1: Numerical Integration Methods
-
Montecarlo Methods to Efficently Compute Volume of Solids by Kamil Czapla, Mariusz Pleszczyński
Автор: kristina_ponomareva














