Шахматные задачи от Поколения

С 1966 года во всем мире 20 июля отмечают Международный день шахмат. В честь недавно прошедшего праздника мы решили написать статью о шахматных задачах из курсов "Поколение Python".

Так получилось, что шахматные задачи являются одной из главных визитных карточек наших курсов. Мы любим эти задачи потому, что они учат строить алгоритмы, находить закономерности, а также позволяют отточить работу с условными (if-else) и логическими (and и or) операторами.

В общем случае шахматные задачи имеют следующий вид:

Даны две различные клетки шахматной доски. Напишите программу, которая определяет, может ли шахматная фигура попасть с первой клетки на вторую одним ходом. Программа получает на вход четыре числа от 1 до 8 каждое, задающие номер столбца и номер строки сначала для первой клетки, потом для второй клетки. Программа должна вывести YES, если из первой клетки ходом фигуры можно попасть во вторую клетку, или NO в противном случае.

У новичков часто возникают трудности с шахматными задачами. Поэтому в этой статье мы рассмотрим некоторые варианты решения каждой из них.

Шахматная доска

Представим шахматную доску в виде поля, где каждая клетка имеет численные координаты х и у. За координату х принимается горизонтальная сторона доски, а за координату у — вертикальная:

Решение любой шахматной задачи начинается с поиска закономерностей в вариантах ходов фигуры на доске.

Ход ладьи ♖

Решаем задачу для ладьи. Шахматная ладья ходит по горизонтали или вертикали.

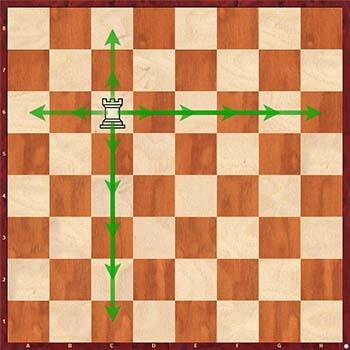
Как мы видим, координаты соответствующих возможным ходам ладьи клеток совпадают по вертикали или по горизонтали. Выявив эту закономерность, можно составить алгоритм решения.

Приведенный ниже код решает поставленную задачу:

x1, y1, x2, y2 = int(input()), int(input()), int(input()), int(input())

if (x1 == x2) or (y1 == y2):
    print('YES')
else:
    print('NO')

Несложно заметить, что условия x1 == x2 и y1 == y2 можно также записать в виде x1 - x2 == 0 и y1 - y2 == 0. Таким образом, одна из этих разностей должна быть равна нулю. Следовательно, условие (x1 == x2) or (y1 == y2) можно заменить на условие (x1 - x2) * (y1 - y2) == 0. Тогда код выше можно записать в таком виде:

x1, y1, x2, y2 = int(input()), int(input()), int(input()), int(input())

if (x1 - x2) * (y1 - y2) == 0:
    print('YES')
else:
    print('NO')

Ход короля ♔

Решаем задачу для короля. Шахматный король ходит по горизонтали, вертикали или диагонали, но только на 1 клетку.

Наиболее простое и прямое решение — это поочередная проверка 8 клеток.

Приведенный ниже код решает поставленную задачу:

x1, y1, x2, y2 = int(input()), int(input()), int(input()), int(input())

if ((x1 - 1 == x2 and y1 + 1 == y2)
    or (x1 == x2 and y1 + 1 == y2)
    or (x1 + 1 == x2 and y1 + 1 == y2)
    or (x1 + 1 == x2 and y1 == y2)
    or (x1 + 1 == x2 and y1 - 1 == y2)
    or (x1 == x2 and y1 - 1 == y2)
    or (x1 - 1 == x2 and y1 - 1 == y2)
    or (x1 - 1 == x2 and y1 == y2)):
    print('YES')
else:
    print('NO')

Несложно заметить, что все проверки в данном решении по сути однотипны, меняются только сдвиги координат относительно начального положения короля. Выявив эту закономерность, можно составить список directions, содержащий пары из чисел -1, 0 и 1, которые описывают направления сдвига относительно короля:

• значение -1 соответствует сдвигу на одну клетку влево по оси x или вниз по оси y

• значение 1 соответствует сдвигу на одну клетку вправо по оси x или вверх по оси y

• значение 0 соответствует отсутствию сдвига

Таким образом, каждая пара чисел в списке представляет одно из восьми возможных направлений движения короля по шахматной доске.

С помощью данного списка и цикла for мы можем реализовать следующую проверку:

x1, y1, x2, y2 = int(input()), int(input()), int(input()), int(input())

directions = [(-1, +1), (0, +1), (+1, +1), (+1, 0), (+1, -1), (0, -1), (-1, -1), (-1, 0)]

for x0, y0 in directions:
    if (x1 + x0 == x2) and (y1 + y0 == y2):
        print('YES')
        break
else:
    print('NO')

На самом деле перебирать все 8 клеток нет никакого смысла. Можно заметить, что координаты клеток, соответствующих возможным ходам короля, отличаются от координат самого короля не более чем на единицу:

x1, y1, x2, y2 = int(input()), int(input()), int(input()), int(input())

if (x1 - 1 == x2 or x1 == x2 or x1 + 1 == x2) and 
    (y1 - 1 == y2 or y1 == y2 or y1 + 1 == y2):
    print('YES')
else:
    print('NO')

Используя встроенную функцию abs(), приведенный выше код можно переписать в таком виде:

x1, y1, x2, y2 = int(input()), int(input()), int(input()), int(input())

if abs(x1 - x2) <= 1 and abs(y1 - y2) <= 1:
    print('YES')
else:
    print('NO')

Ход слона ♗

Решаем задачу для слона. Шахматный слон ходит по диагоналям.

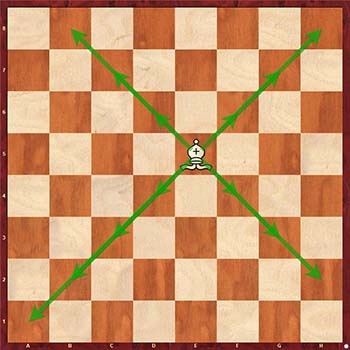
При поиске закономерностей в координатах клеток диагоналей можно заметить, что условиеx1 - y1 == x2 - y2 соответствует одной диагонали, а условие x1 + y1 == x2 + y2 — другой диагонали. Так как слон ходит по обеим диагоналям, то следует использовать логический оператор or:

x1, y1, x2, y2 = int(input()), int(input()), int(input()), int(input())

if (x1 - y1 == x2 - y2) or (x1 + y1 == x2 + y2):
    print('YES')
else:
    print('NO')

Условия x1 - y1 == x2 - y2 и x1 + y1 == x2 + y2 можно записать в виде x1 - x2 == y1 - y2 и x1 - x2 == -(y1 - y2).

Так как из равенства модулей |a| = |b| следуют равенства a = b и a = -b, то используя встроенную функцию abs(), приведенный выше код можно переписать в таком виде:

x1, y1, x2, y2 = int(input()), int(input()), int(input()), int(input())

if abs(x1 - x2) == abs(y1 - y2):
    print('YES')
else:
    print('NO')

Несложно заметить, что вместо модулей можно использовать и квадраты, ведь из равенства квадратов также следуют равенства a = b и a = -b:

x1, y1, x2, y2 = int(input()), int(input()), int(input()), int(input())

if (x1 - x2) ** 2 == (y1 - y2) ** 2:
    print('YES')
else:
    print('NO')

Ход ферзя ♕

Решаем задачу для ферзя. Шахматный ферзь ходит по диагонали, горизонтали или вертикали.

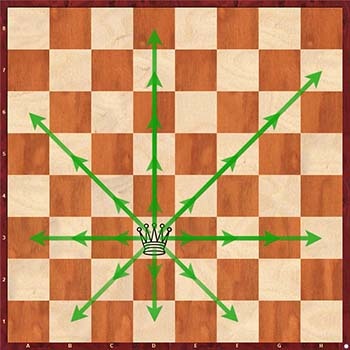
Несложно заметить, что варианты ходов ферзя включают варианты ходов ладьи и слона. Следовательно, для решения задачи мы можем комбинировать условия, которые использовали для решения задач с ходами ладьи и слона.

Приведенный ниже код решает поставленную задачу:

x1, y1, x2, y2 = int(input()), int(input()), int(input()), int(input())

if (x1 - x2) * (y1 - y2) == 0 or abs(x1 - x2) == abs(y1 - y2):
    print('YES')
else:
    print('NO')

Ход коня ♘

Решаем задачу для коня. Шахматный конь ходит буквой "Г".

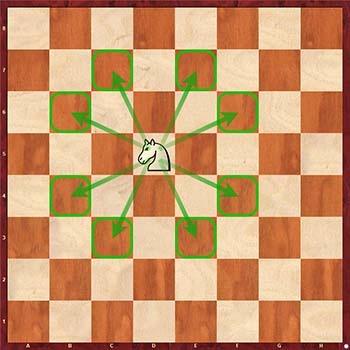
Задача с конем похожа на задачу с королем. Мы можем аналогичным образом решить ее с использованием 8 условий.

Приведенный ниже код решает поставленную задачу:

x1, y1, x2, y2 = int(input()), int(input()), int(input()), int(input())

if ((x1 - 2 == x2 and y1 + 1 == y2)
    or (x1 - 1 == x2 and y1 + 2 == y2)
    or (x1 + 1 == x2 and y1 + 2 == y2)
    or (x1 + 2 == x2 and y1 + 1 == y2)
    or (x1 + 2 == x2 and y1 - 1 == y2)
    or (x1 + 1 == x2 and y1 - 2 == y2)
    or (x1 - 1 == x2 and y1 - 2 == y2)
    or (x1 - 2 == x2 and y1 - 1 == y2)):
    print('YES')
else:
    print('NO')

Как и в задаче с королем, все проверки в данном решении по сути однотипны, меняются только сдвиги координат относительно начального положения коня. Выявив эту закономерность, можно составить список directions, содержащий пары из чисел -2, -1, 1 и 1, которые описывают направления сдвига относительно коня.

С помощью данного списка и цикла for мы можем реализовать следующую проверку:

x1, y1, x2, y2 = int(input()), int(input()), int(input()), int(input())

directions = [(-2, 1), (-1, 2), (1, 2), (2, 1), (2, -1), (1, -2), (-1, -2), (-2, -1)]

for x0, y0 in directions:
    if (x1 + x0 == x2) and (y1 + y0 == y2):
        print('YES')
        break
else:
    print('NO')

Однако, как и в задаче с королем, перебирать все 8 клеток нет никакого смысла. Можно заметить, что произведение разности соответствующих координат по модулю всегда равно 2, поэтому мы можем записать следующее условие:

x1, y1, x2, y2 = int(input()), int(input()), int(input()), int(input())

if abs((x1 - x2) * (y1 - y2)) == 2:
    print('YES')
else:
    print('NO')

Кроме описанных выше способов решения мы также можем использовать подход, основанный на вычислении расстояния между точками. Действительно, квадрат расстояния между точкой с начальными координатами коня и точкой, соответствующей одному из возможных ходов, всегда равен 5:

x1, y1, x2, y2 = int(input()), int(input()), int(input()), int(input())

if (x1 - x2) ** 2 + (y1 - y2) ** 2 == 5:
    print('YES')
else:
    print('NO')

Расстояние между точками и вычисляется по формуле:

Заключение

Шахматные задачи являются одним из лучших способов тренировки алгоритмического мышления для начинающих программистов. В статье мы рассмотрели различные варианты их решения.

Пишите в комментариях свои варианты, если они отличаются от наших.

Присоединяйтесь к нашему телеграм-каналу, будет интересно и познавательно!

❤️ Happy Pythoning! 🐍