История одной очереди

В одно воскресенье довелось мне стоять в очереди на избирательный участок №8134 в Алматы. Простоял я там 4 часа, а некоторые и того больше. И как-то совершенно случайно вспомнил, что в институте я учился на специальности “системы и сети массового обслуживания”, а тут у нас как раз такая сеть, которую можно попробовать рассчитать. А заодно ответить расчётами на следующие вопросы:

• Могло ли действительно через УИК пройти указанные в итоговом протоколе 1830 человек?

• Могло ли через УИК пройти меньшее число людей, какова нижняя граница?

• Могло ли через УИК пройти большее число людей, какова верхняя граница?

• Могло ли через УИК пройти 7500 человек (именно столько бюллетеней указано в официальных данных)?

Исходные данные

Разделю на три группы - факты, результаты опроса, наблюдения и предположения

Факты

• УИК выдала 1830 бюллетеней избирателей из 7500 имевшихся у неё

• В УИКе было 2 кабинки для голосования, и 4 сотрудника, регистрировавших избирателей и выдававших бюллетени

• На входе в УИК была одна рамка и один сотрудник с ручным металлоискателем

• По свидетельствам основная масса людей пришла в период с 10.00 по 14.00 - именно тогда сформировалась большая очередь

• Максимальная длина очереди была порядка нескольких сотен, если не тысяч

Результаты опроса

Я провёл небольшой опрос среди тех, кто приходил в тот день. К сожалению, для моего участка (8134) данных собралось немного, 12 записей, из которых не все подходили для анализа. Плюс вопросы я задавал не совсем корректные в силу неопытности. Но кое-что из опроса подчерпнуть можно:

• Время досмотра у охраны - от 15 до 60 секунд. Среднее - 27.5 секунд.

• Досмотр одновременно проходил один избиратель, остальные ждали

  • У одного опрошенного был ответ, что кроме него досмотр проходили 3 человека, но скорее всего он имел ввиду стояние в очереди на досмотре, т.к. сотрудник с ручным металлоискателем был только один

• Внутри УИКа в 60% случаев не приходилось ждать вовсе, в остальных случаях ожидание длилось недолго. Можно считать, что очередей внутри не было.

• Время, проведённое в очереди среди тех, кто пришёл после 11.00 - от 4 до 6 часов. 

  • Пришедшие в 11.45 стояли 4 часа

  • Пришедшие в 12.30 стояли 6 часов

• Те, кто пришёл до 10.00 - если и стояли, то меньше часа

Наблюдения и предположения

• Каждый сотрудник УИКа записывал данные избирателя в журнал ручкой и выдавал бюллетень. Предположу, что это занимало от 30 до 120 секунд, со всеми “Здравствуйте”, “До свидания” и прочими заминками.

• Каждый избиратель проводил в кабинке для голосования от 5 до 60 секунд

• Охрана не только досматривала, но и контролировала численность избирателей на участке, прося подождать

Изображение нашей сети массового обслуживания

Сеть получается очень простая, разомкнутого типа. Всего 3 узла, соединённых последовательно:

• Охрана - один “обслуживающий прибор”

• Сотрудники УИК - четыре “обслуживающих прибора”

• Кабинки для голосования - два “обслуживающих прибора”

Для расчётов я возьму свой же диплом - приложение ITMOdel (кажется, оно даже используется в ИТМО, но я не знаю точно) - и вобью туда свои предположения. В качестве интенсивности источника заявок возьму искомое число бюллетеней (1830) и поделю на время работы УИКа (13 часов, с 8 утра до 21 вечера) - получится 0,0391025641025641 человек в секунду.

Для всех узлов возьмём среднее время обработки - 27.5с для охраны, 75.5с для сотрудников, и 32.5с для кабинок.

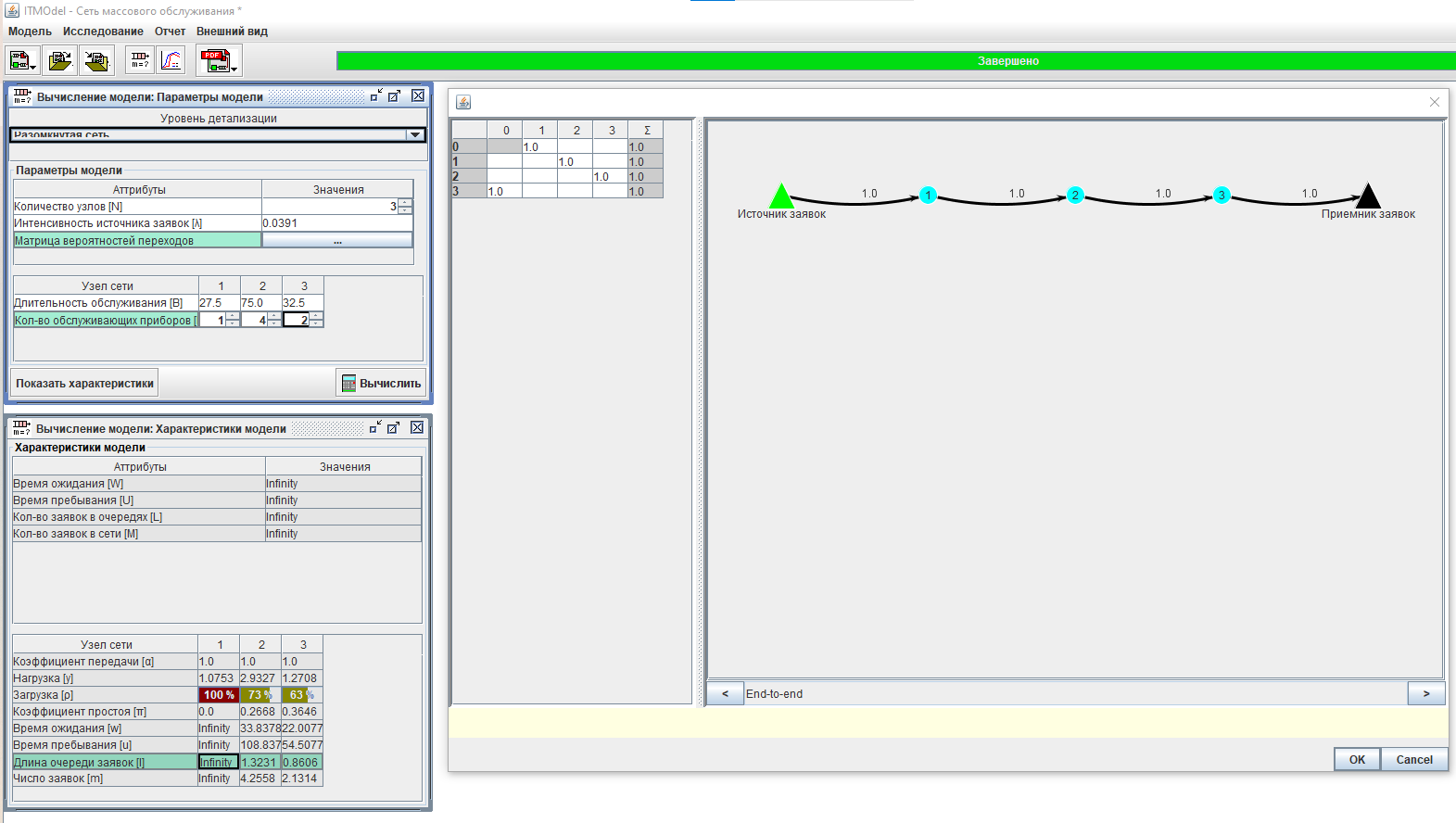
Хм. Если брать такие числа, то получается, что охрана не справлялась с работой, и 1830 бюллетеней обработанно быть не могло.

Но не будем делать выводы, т.к. часть данных у нас прикидочные. Попробуем их уточнить.

Симуляция и поиск подходящих параметров

Я набросал небольшой симулятор на питоне, который создаёт заявки, гоняет их по узлам обработки, собирает статистику, и ещё делает красивые анимации процесса:

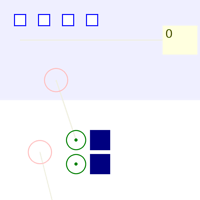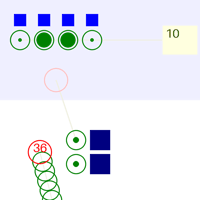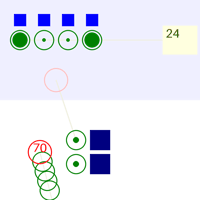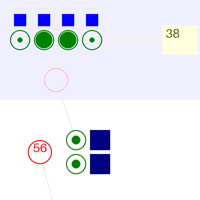
Для начала забьём в него те же данные, что в рассчётную модель выше. Результаты получаются такими:

model_uik(
   guard_processing_time=27.5,
   registrator_processing_time=75.5,
   box_processing_time=32.5,
   requests_total=1830,
   print_log=True
)

[xx] Max Guard Queue Length: 128
[OK] Max UIK queue Length: 0
[OK] Max Guard Queue Waiting Time: 0.92h
[xx] 11:45 Queue Waiting Time: 0.28h
[xx] 12:30 Queue Waiting Time: 0.33h
[OK] Processed: 1698
    Came: 1830
    Guard Load: 100.00%
    Registrators Load: 68.59%
    Boxes Load: 58.98%

На длины очередей можно внимания не обращать, но % загрузки в целом похожи. Самое главное тут то, что узел охраны не справляется с нагрузкой при заданной средней длительности обслуживания. 

Если попробовать взять значения поменьше (допустим, что охрана в среднем быстрее работала), то уже что-то вырисовывается - при среднем значении 25.5с модель начинает успевать обрабатывать заявки.

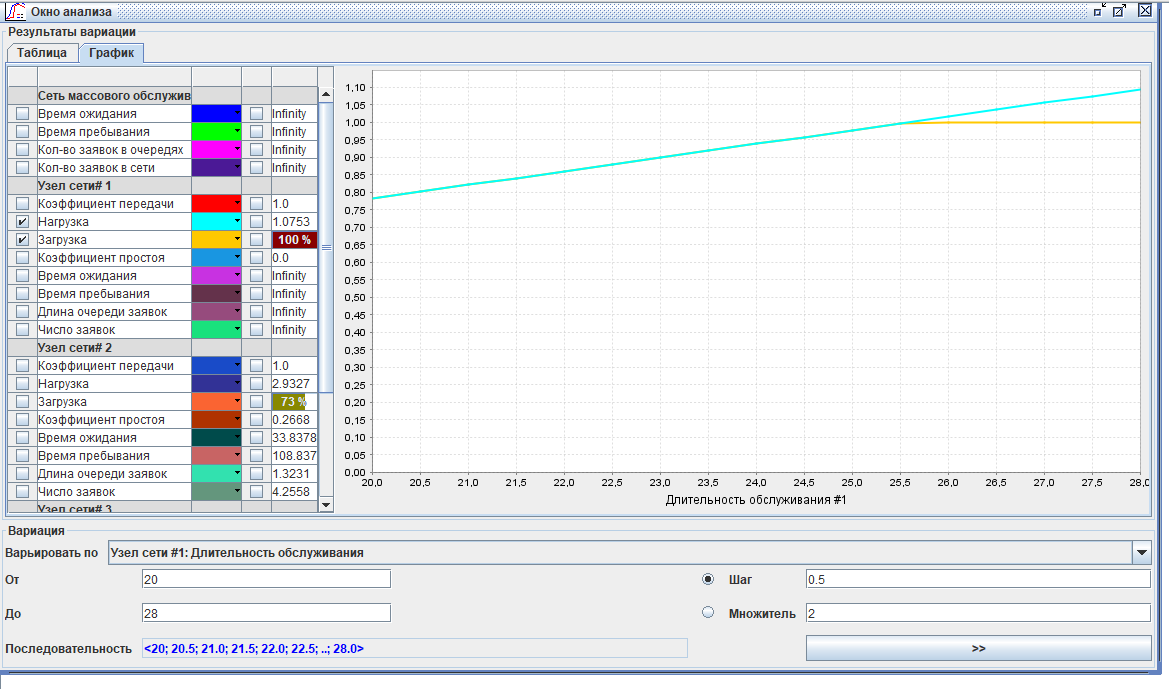
[xx] Max Guard Queue Length: 0
[OK] Max UIK queue Length: 1
[OK] Max Guard Queue Waiting Time: 0.00h
[xx] 11:45 Queue Waiting Time: 0.00h
[xx] 12:30 Queue Waiting Time: 0.00h
[OK] Processed: 1826
    Came: 1830
    Guard Load: 99.69%
    Registrators Load: 73.72%
    Boxes Load: 63.43%

Но это скорее гадание на кофейной гуще, а хочется получить данные, совпадающие с тем, что мы знаем об очереди.

Таким образом были поставлены следующие требования к модели:

• Максимальная очередь к охране должна быть больше 500. Вообще там было ближе к тысяче, но возьмём нижнюю границу за 500 

• Максимальная очередь внутри УИК-а должна быть меньше 4.

• Заявки, вставшие в очередь в районе 11.45, должны простоять 4 часа (или около того)

• Заявки, вставшие в очередь в районе 12:30, должна простоять 6 часов (или около того)

• Максимальное время ожидания в очереди не должно превышать 8 часов

Можно увидеть, что модель выше, хоть и обеспечивает обработку нужного числа заявок за 13 часов, не даёт той картины, которая была в реальности. Возможно это связано с тем, что люди приходили неравномерно. Я выделил 3 периода времени:

• С 8 до 10 - предположительно низкая интенсивность

• С 10 до 14 - предположительно высокая интенсивность. Назову это "большая очередь"

• С 14 до 21 - предположительно низкая интенсивность

Думаю, тут хорошо подошёл бы метод градиентного спуска, если из требований выше составить хорошую функцию расстояния. Но, если честно, мне было лениво этим заниматься, так что я просто рандомно сгенерировал 500 тысяч параметров модели, прогонял симуляцию, и выбрал из них подходящие под условия.

Получилось у меня 722 варианта модели. Из них 4 варианта описывали модель так, что на выходе получалось около тех самых 1830 человек. 

Ожидаемо, время работы охраны тут было решающим, и составило около 25 секунд. Прочие времена обработок варьировались обширнее.

Возьмём самую первую строчку и посмотрим на результаты симуляции поподробнее.

[OK] Max Guard Queue Length: 1533
[OK] Max UIK queue Length: 4
[OK] Max Guard Queue Waiting Time: 7.83h
[OK] 11:45 Queue Waiting Time: 4.29h
[OK] 12:30 Queue Waiting Time: 6.15h
[OK] Processed: 1842
    Came: 2871
    Guard Load: 91.84%
    Registrators Load: 86.31%
    Boxes Load: 78.80%

Получили максимальную очередь в 1.5 тысячи человек, подходящие времена ожидания, и принятые 1842 человека, хотя пришли 2871.

Если прогнать ту же модель через расчёты, то получим такую картину:

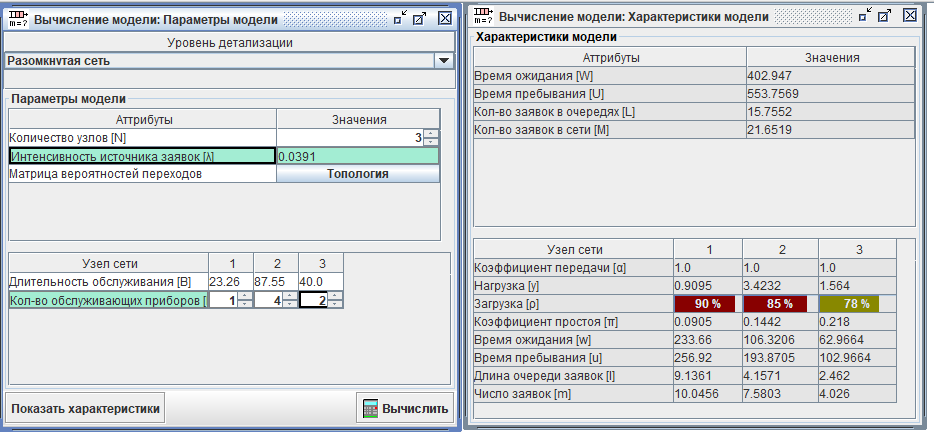
Опять же, коэффициенты загрузки совпадают. Для нас это хорошо тем, что можно проверить разные варианты не гоняя симуляцию. Хотя симуляция может дать более красивые картинки. Вот, например, график зависимости времени выхода от времени входа.

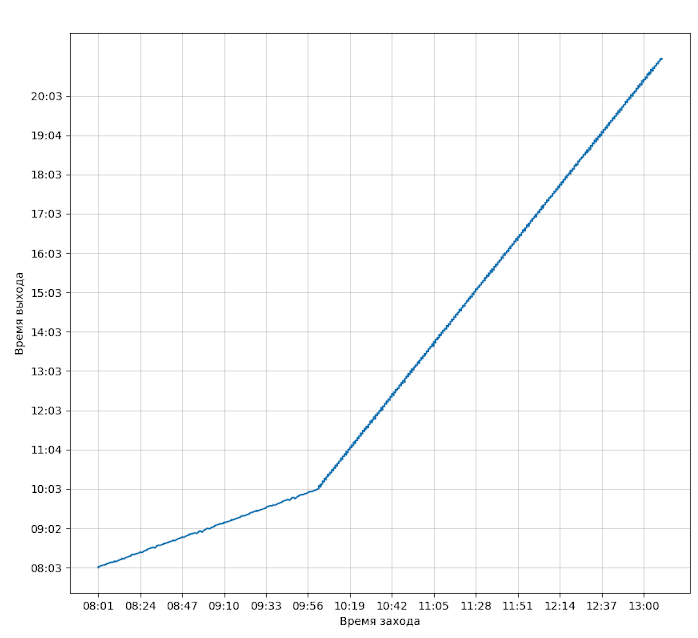
Он не спроста обрывается в районе 13.00. Походу все, кто пришли позже, в УИК не попали.

А вот анимация:

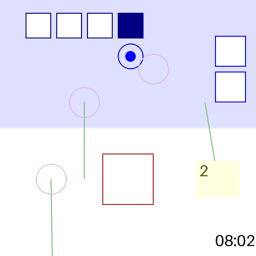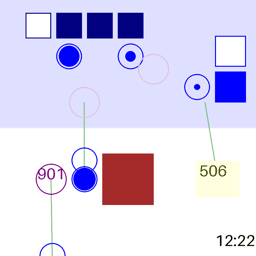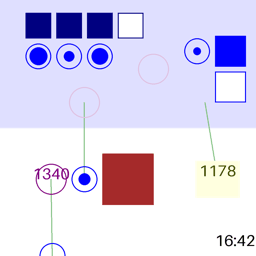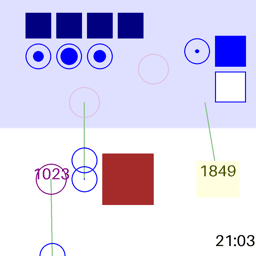
Внизу охрана, вверху - регистраторы, справа - кабинки для голосования. В жёлтом прямоугольнике - количество вышедших избирателей.

Так, а в данных у нас были ещё варианты. Например, последняя строчка забавная.

Там пришло почти 9000 человек, а результат такой же. Прогоним на симуляции:

[OK] Max Guard Queue Length: 7113
[OK] Max UIK queue Length: 1
[OK] Max Guard Queue Waiting Time: 7.72h
[OK] 11:45 Queue Waiting Time: 4.47h
[OK] 12:30 Queue Waiting Time: 6.04h
[OK] Processed: 1890
    Came: 9007
    Guard Load: 100.00%
    Registrators Load: 78.31%
    Boxes Load: 44.92%

И посмотрим на график длины очереди по времени:

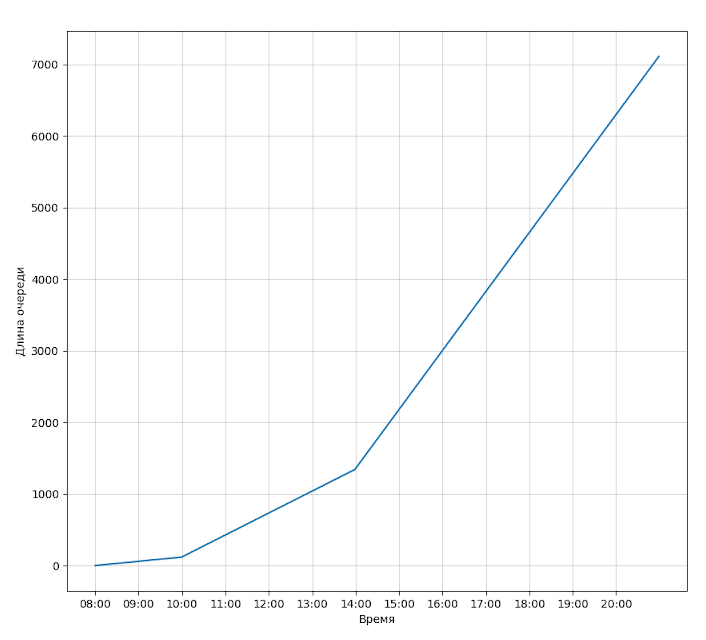
И на график времени входа/выхода:

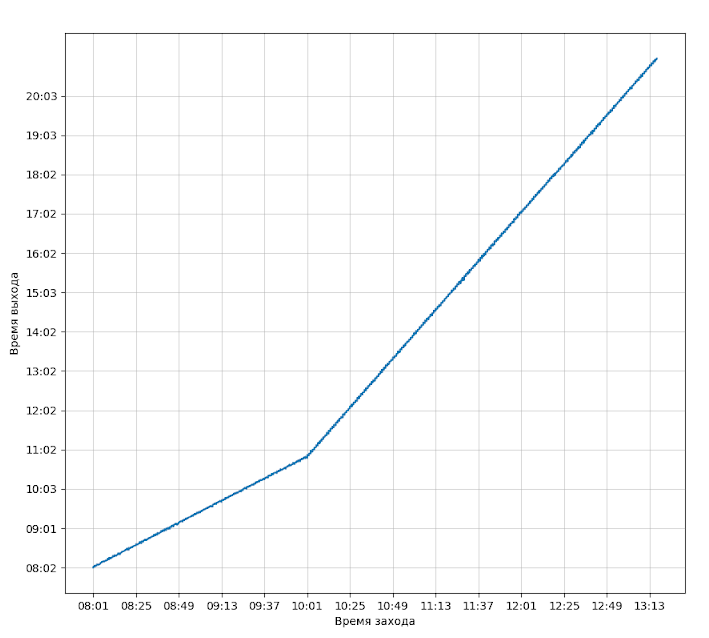
В общем, результат понятен. Люди, пришедшие после 14.00, в этой модели не попали в УИК вообще, следовательно их можно хоть миллиард, хоть 0 в этот период пригнать - результат не изменится.

Поиск нижней границы

Понятно, что в общем смысле нижняя граница - это 0. Достаточно просто время досмотра выставить в 14 часов, и всё.

Но нас интересует именно вариант, при котором соблюдаются все условия заданные выше. То есть какое минимальное число голосующих мог принять УИК, воспроизведя такую же очередь.

При переборе 500 тысяч вариантов был найден такой вариант, с минимальным количеством принятых избирателей.

3 минуты досмотра на человека, неплохо! В итоге получаем достаточно большую очередь, те же времена стояния, и всего 210 принятых избирателей. В общем, могли бы и хуже!

[OK] Max Guard Queue Length: 809
[OK] Max UIK queue Length: 0
[OK] Max Guard Queue Waiting Time: 7.83h
[OK] 11:45 Queue Waiting Time: 4.17h
[OK] 12:30 Queue Waiting Time: 6.19h
[OK] Processed: 210
    Came: 1021
    Guard Load: 88.49%
    Registrators Load: 17.88%
    Boxes Load: 16.68%

Поиск верхней границы

Вот такой вариант был найдет при переборе:

Тут у нас сверх-скоростная охрана, которая тратит 9 секунд на человека, и регистратор, который за 12 секунд успевает переписать ФИО, паспортные данные и адрес. При таких фантастических вводных УИК мог бы принять больше 5000 избирателей, сохраняя все признаки той очереди, которую мы видели:

[OK] Max Guard Queue Length: 4111
[OK] Max UIK queue Length: 0
[OK] Max Guard Queue Waiting Time: 7.80h
[OK] 11:45 Queue Waiting Time: 4.30h
[OK] 12:30 Queue Waiting Time: 6.11h
[OK] Processed: 5471
    Came: 7325
    Guard Load: 100.00%
    Registrators Load: 35.29%
    Boxes Load: 88.22%

Очередь в 4000 человек, боюсь, не поместилась бы на близлежащих улицах.

Что надо было бы сделать в УИК чтобы принять 7500 человек

Но давайте возьмём найденные “реалистичные” параметры, и попробуем понять - что нужно было сделать, чтобы УИК смог принять 7500 избирателей - столько, сколько у них было заготовлено бюллетеней?

Воспользуемся расчётами в ITMOdel. 7500 избирателей за 13 часов - это примерно 0.1603 человека в секунду. 

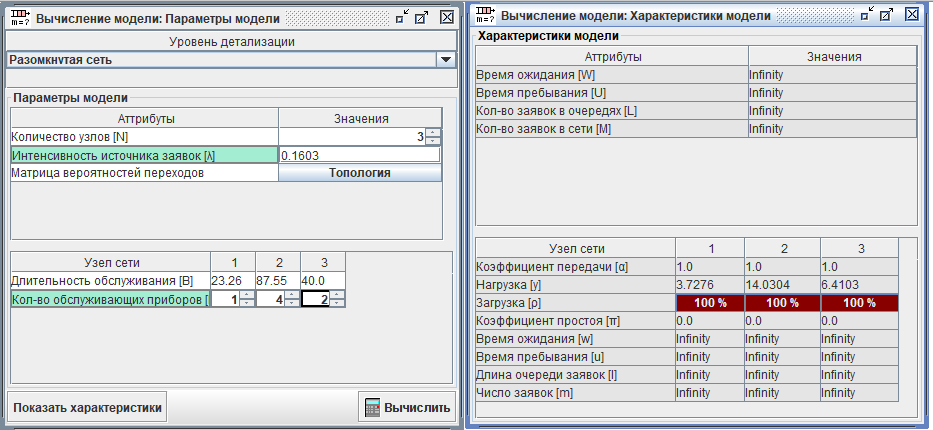
Ожидаемо, с такой нагрузкой в текущей комплектации УИК не справился бы. 

Коэффициент “нагрузки” справа как бы намекает нам, сколько должно быть “обслуживающих приборов”, чтобы система могла обработать все заявки.

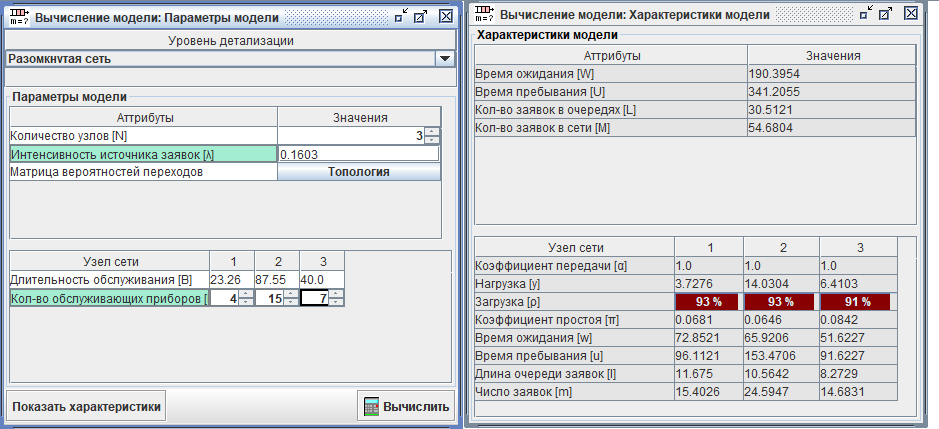
Итого, должно было быть

• 4 охранника, производящих досмотр (а не 1)

• 15 сотрудников, выполняющих регистрацию избирателей (а не 4)

• 7 кабинок для голосования (а не 2)

Почему сотрудники УИК-а, рассчитывая на 7500 избирателей, не озаботились обеспечением такой пропускной способности - загадка.

Выводы

Вспомним заданные в начале статьи вопросы:

• Могло ли действительно через УИК пройти указанные 1830 человек?

  • Ответ: да, могло

• Могло ли через УИК пройти меньшее число людей, какова нижняя граница?

  • Ответ: да, можно было и 200 человек принять

• Могло ли через УИК пройти большее число людей, какова верхняя граница?

  • Ответ: при наличии в охране Супермена, а за столиками регистрации Флэшей - можно было принять и 5000 человек

• Могло ли через УИК пройти 7500 человек (именно столько бюллетеней указано в официальных данных)?

  • Ответ: нет, не могло при имеющихся условиях. Нужно было в 4 раза увеличить количество охранников, регистраторов и кабинок.

Заключение

Наверное, вас интересует - зачем это? Что с этой информацией теперь делать?

Если честно, я не знаю. Я чувствую себя так, как Адам Дженсен на этой картинке:

В школе меня учили, что 2+2=4, а за 2+2=5 ставят двойку. В институте меня учили считать системы и сети массового обслуживания, рассчитывать длины очередей. 

Ни там, ни там меня не учили, что делать, когда ты прокачал математику и всё рассчитал, а оппонент прокачал наглость, силу и возможность говорить мне в лицо, что 2+2=87%.

Это бессилие и отчаяние, которое я и пытаюсь заполнить занятными вычислениями, которые, к сожалению, ничего не изменят..

Исходные данные можно найти тут

Симулятор - тут

Данные с УИК - тут . Из-за рубежа без VPN не получится посмотреть.