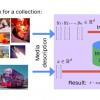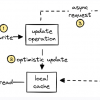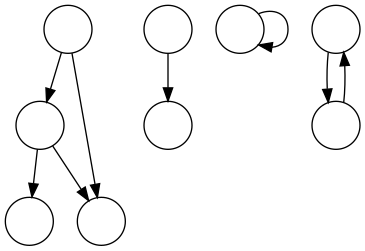
Все графы созданы с помощью graphviz (источник)
В сфере разработки ПО графы используются повсеместно:
- Зависимости пакетов, как и импорт модулей, формируют направленные графы.
- Интернет — это граф, состоящий из ссылок между веб-страницами.
- При проверке моделей анализ выполняется путём изучения «пространства состояний» всех возможных конфигураций. Узлы — это состояния, а рёбра — это допустимые переходы между ними.
- Реляционные базы данных — это графы, в которых узлы являются записями, а рёбра — внешними ключами.
- Графы — это обобщение связанных списков, двоичных деревьев и хэш-таблиц.1
Кроме того, графы также широко используются в бизнес-логике. Научные работы со ссылками формируют графы цитат. Транспортные сети представляют графы маршрутов. Социальные сети — это графы связей. Если вы работаете в сфере разработки, то рано или поздно встретитесь с графами.
Я вижу графы повсюду и использую их для анализа всевозможных систем. В то же время я побаиваюсь использовать их в коде. Какой из популярных языков программирования ни возьми, поддержка графов в них практически отсутствует. Ни в одном её нет в виде встроенного типа, очень мало где они прописаны в стандартной библиотеке, и у многих языков нет для этой функциональности надёжного стороннего пакета. Чаще всего мне приходится создавать графы с нуля. Существует большой разрыв между тем, как часто инженерам ПО могут понадобиться графы и тем, в какой степени экосистема их поддерживает. Где все графовые типы?
По мере того как я всё чаще сталкивался с графами в своей работе, этот вопрос волновал меня всё больше. В итоге осенью прошлого года я, наконец-таки, решил найти на него ответ. Я обратился с призывом к диалогу к своим читателям, имеющим релевантный этой теме опыт — к разработчикам алгоритмов графов, членам комитетов по языкам программирования и мейнтейнерам библиотек графов. Я планировал побеседовать с десятком людей, но в итоге мне хватило четверых:
- Заенц: бывший разработчик решателя задач удовлетворения ограничений Gecode, который также «реализовал все известные алгоритмы графов».
- Брэдфорд: автор библиотеки безопасности Nosey Parker и изобретатель нескольких новых графовых алгоритмов.
- Николь: бывший инженер графовой базы данных.
- Келли: мейнтейнер графовой библиотеки NetworkX и разработчик компилятора.
Получив от всех этих четырёх человек похожие ответы, я понял, что продолжать интервью смысла нет и приступил к написанию статьи.
Причины
▍ Слишком много вариантов дизайна
Выше я говорил про направленные графы, но существуют ещё и ненаправленные, в которых рёбра не имеют конкретного направления. Оба вида графов могут быть либо простыми, имеющими максимум одно ребро между двух узлов, либо мультиграфами, в которых между узлов может быть много рёбер. Кроме того, оба этих типа графов бывают гиперграфами, где ребро может соединять три и более узлов, или уберграфами, в которых рёбра могут указывать на другие рёбра. Причём для каждого из этих видов существуют разные варианты реализации: будете ли вы присваивать ID только узлам или рёбрам тоже? Какие данные могут храниться в узле, а какие в ребре?
Получается, что библиотека должна включать в себя огромное число решений.
Но, подождите-ка… А эти различия вообще имеют значение? Простой граф — это всего-навсего упрощённый мультиграф, а ненаправленное ребро можно без потерь превратить в два направленных. Язык мог бы просто предоставлять направленные гиперубермультиграфы, давая пользователям возможность ограничивать их до нужных параметров.
Но у этого подхода есть две проблемы. Во-первых, он подразумевает изменение интерфейса в том плане, что разные операции будут возвращать либо единичные значения, либо списки. Во-вторых, как я поясню позже, важными аспектами являются быстродействие графовых алгоритмов и особые случаи. Келли привёл в качестве примера паросочетание с максимальным весом. Если вам известно, что ваш граф двухдольный, то вы можете использовать для поиска паросочетания быстрый алгоритм. А вот для других графов потребуется использовать медленный, более обобщённый алгоритм.
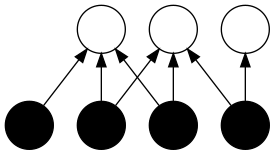
Двухдольный граф (источник)
«Это подводит нас к проблеме выбора алгоритма. Допустим, у нас есть задача P, граф G и алгоритмы A, B, С для решения P на G…какой из них выбрать? Если нам не известно, что G двухдольный, а алгоритм С работает только для двухдольных графов, то сколько времени мы можем выделить на определение того, является ли G таковым?», — Келли.
Идеальная графовая библиотека должна поддерживать много разных видов графов. Но тогда потребуется уйма времени на поддержку всех тех возможностей, которые люди хотят от них получить. Графовые алгоритмы невероятно сложно реализовать правильно. В этой статье создатель Python описал создание собственного алгоритма find_shortest_path, в который пришлось пять раз вносить изменения!
«Каждая реализация pagerank, с которой я проводил сравнение, оказывалась ошибочной», — Николь.
Так какие алгоритмы должны присутствовать в библиотеке? «То количество задач, какое люди хотят решать с помощью графов, просто абсурдно», — сказал мне Келли. И это согласуется как с моим опытом, так и с опытом всех, кого я опросил. Порой кажется, что графы имеют слишком большие возможности, которые буквально выходят за грани моего понимания. «Вопрос в том, где вы решите провести грань?», — подытожил Келли.
Для NetworkX «грань» означает примерно 500 разных графовых алгоритмов, которые сами по себе уже потребуют 60,000 строк кода. К сравнению, вся стандартная библиотека Python, состоящая из 300 пакетов, содержит около 600,000 строк.2
В свете всего этого неудивительно, что вы не встречаете графы в стандартных библиотеках. Мейнтейнерам языка пришлось бы решать, какие виды графов поддерживать, какие топологии отнести к особым случаям и какие включить алгоритмы. Есть смысл переложить эту работу по обслуживанию на сторонних лиц, что уже является передовым трендом в разработке языков. Даже Python, известный тем, что идёт с «батареями в комплекте», удаляет 20 из своих батарей.
Сторонние лица могут принимать однозначные решения в отношении того, как проектировать графы и какие включать алгоритмы. Но тогда перед ними возникает другая проблема: как представить графовый интерфейс?
▍ Слишком много вариантов реализации
Представим, что мы поддерживаем только самые простые направленные графы: у узлов есть идентификаторы, у рёбер нет, ни те ни другие не имеют связанных данных. Как такой граф закодировать?
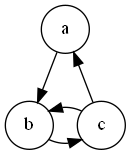
Вот четыре возможных способа, которыми язык программирования может его внутренне сохранить:
- Список рёбер:
[[a, b], [b, c], [c, a], [c, b]]. - Список смежности:
[[b], [c], [a, b]]. - Матрица смежности:
[0 1 0; 0 0 1; 1 1 0]. - Набор из трёх структур со ссылками друг на друга.
Разные графовые операции в разных представлениях имеют разные характеристики быстродействия. Возьмём, к примеру, граф со 100 узлами и 200 рёбрами. Если использовать представление в виде матрицы смежности, то потребуется матрица 100х100, содержащая 200 единиц и 9800 нулей. Если же взять список рёбер, то потребуется всего 200 пар узлов. В зависимости от вашего процедурного языка и уровня оптимизаций, это отличие может составить 20-кратную разницу в потреблении памяти.
Теперь возьмём граф со 100 узлами и 8000 рёбрами и попробуем выяснить, существует ли ребро между узлом 0 и узлом 93. В представлении матрицы это будет поиск со сложностью О(1) по graph[0][93]. В случае списка рёбер это будет перебор O(|ребро|) по всем 8000 рёбрам.3
Если в графе есть всего несколько рёбер, то он является разрежённым. Если же в нём проложены почти все возможные рёбра, то такой граф является плотным. Одной и той же программе может потребоваться выполнять обе операции на обеих топологиях графов: если вы создаёте граф из внешних данных, то можете начать с разрежённого графа и позднее получить плотный. Для внутреннего представления графа не существует «правильного варианта».
И все эти сложности мы наблюдаем при работе с самым простым направленным графом. А как насчёт реализации данных узлов? Данных рёбер? Различных типов узлов и рёбер? Большинство сторонних библиотек можно грубо разделить на две категории:
- Предлагает один обогащённый тип данных, охватывающий все случаи ценой эффективности. Например, NetworkX сохраняет граф в виде словаря словарей словарей, чтобы узлы и рёбра могли содержать произвольные данные.4
- Предлагает отдельные типы графов для каждого представления и возлагает на пользователя ответственность за сохранение данных узлов и рёбер отдельно от типа графа.
Примером второго случая является Petgraph, самая популярная графовая библиотека для Rust. В ней есть graph, graphmap и matrix_graph для разных случаев. Брэдфорд использовал Petgraph для Nosey Parker, инструмента безопасности, сканирующего всю историю репозитория Git на наличие секретов. Для бенчмарка он использовал граф CPython, который содержит 250 К коммитов и 1,3 М объектов, но всего по несколько рёбер на узел коммита. Он остановился на списке смежности.
Поддержка множества представлений имеет серьёзный недостаток: вам приходится проделывать много работы по добавлению алгоритмов. Создавая отдельную версию алгоритма для каждого представления графа, вы утраиваете или учетверяете дальнейшую нагрузку по обслуживанию. Если же вы, напротив, напишете общую абстракцию для полиморфных типов, то ваша библиотека окажется менее производительной. Один из программистов, с кем я не эту тему беседовал, прикинул, что самописный графовый алгоритм может оказаться в 20 и более раз быстрее обобщённого алгоритма.
И этот довод в беседе с каждым из упомянутых выше специалистов звучал как серьёзная проблема.
▍ Производительность слишком важна
«Обобщённая реализация графа зачастую не справляется», — Брэдфорд.
Это веский аргумент.
Очень многие графовые алгоритмы являются NP-полными или даже труднее.5 И хотя NP-полнота в случае крупных задач далеко не всегда означает сверхсложность, графы могут представлять огромные задачи. Выбор представления, как и деталей реализации алгоритма, играет важную роль в том, как быстро вы сможете его завершить.
У каждого, с кем я беседовал, нашлась история на этот счёт. В Nosey Parker Брэдфорду нужно было воссоздавать снимок файловой системы для каждого коммита, что означало обход графа объектов. Ни один из имеющихся инструментов обхода не смог масштабироваться на его случай. В итоге ему пришлось «на коленке» разработать почти полностью новый алгоритм, который сократил объём потребляемой памяти в тысячу раз.
«Я смог довольно быстро реализовать рабочий прототип с помощью Petgraph, но потом… Это оказался тот случай, когда ты сталкиваешься с реальностью ограничений производительности», — Брэдфорд.
Заенц описал другую проблему: «Что, если граф окажется просто слишком велик для использования?» Он привёл пример поиска решения в «пятнашках». Она решается через выполнение поиска А* по пространству состояний, которое содержит более 20 триллионов вариантов.
«Если вы просто сгенерируете все узлы, то уже проиграете», — Заенц
Заенц курировал исследовательский проект по добавлению графов в Gecode. В конечном итоге он выяснил, что обобщённый тип графа просто не может сравниться с ручным выбором представления для задачи.
Эта проблема присуща даже графовым базам данных, спроектированным полностью на основе сложных графовых алгоритмов. Николь, инженер графовой базы данных, рассказала мне о некоторых проблемах с оптимизацией даже простых операций на графах.
«Если вы выполняете обход, то вам нужно либо ограничить глубину, либо смириться с обходом всего графа. При поиске в глубину вроде пройти три шага от этой точки, чтобы найти путь, если он существует, вы уже сталкиваетесь с обходом приличного объёма данных», — Николь.
Уволившись с этой работы, Николь работала консультантом по вопросам быстродействия запросов к графам. Обычно это означало переход с графовой базы данных на иное решение, и она рассказала мне об одном таком проекте. Для ускорения графовых запросов Николь оставила лишь одно вычисление нетронутым и переписала всё остальное в виде процедур MapReduce. «С точки зрения понимания всё усложнилось, зато обработка стала мгновенной», — вспоминала она.
Всё это означает, что если вы хотите решать графовые задачи, то вам потребуется хороший контроль над деталями представления ваших данных и алгоритма. Производительность в качестве разменной монеты вы себе позволить не можете.
▍ Выводы оказались единогласны
Итак, причины, по которым у нас нет масштабной поддержки графов:
- существует много видов графов;
- для каждого вида есть много разных представлений;
- существует много графовых алгоритмов;
- производительность графовых алгоритмов очень чувствительна к графовому представлению и деталям реализации;
- люди используют очень затратные алгоритмы для очень больших графов.
Становится ясно, почему языки не поддерживают графы в своих стандартных библиотеках: слишком много решений дизайна, компромиссов и хлопот с обслуживанием. Это объясняет, почему программисты избегают использования сторонних графовых библиотек — потому что они либо слишком ограничены, либо слишком медлительны. Это также объясняет, почему программисты не любят рассуждать в контексте графов, за исключением крайних случаев — слишком уж сложно с ними работать.
С начала этого исследования я в своей работе столкнулся с несколькими новыми задачами на графах. Я по-прежнему ценю анализ систем в виде графов и при этом боюсь их реализовывать. Но теперь я знаю, почему их боятся и все остальные. Спасибо вам за внимание!
Дополнение: языки с графовыми типами
▍ Языки запросов к графам
Языки запросов к графам (Graph querying languages, GQL) 6 являются для графовых баз данных тем же, чем SQL — для реляционных. Здесь нет широко используемого стандарта, но в качестве двух наиболее популярных можно выделить SPARQL для запросов к семантическим тройкам и cypher в Neo4j. Иронично, но GraphQL не является языком запроса к графам. Его название объясняется связью с Facebook Graph Search. Я считал графовые базы данных сильно отличающимися от графов в языках программирования, но их языки запросов показывают, что графы могут работать в процедурном языке.
Основное отличие между всеми GQL и SQL в том, что связи в GQL являются сущностями первого класса. Представьте себе датасет фильмов и людей, в котором люди выступают в качестве актёров, режиссёров или продюсеров этих фильмов. В SQL вы бы реализовали каждую связь в виде таблицы «многие-ко-многим», что упростило бы запрос «кто снимался в фильме Х», но усложнило запрос вроде «кто снимался в фильме Y и в какой роли». В SPARQL связи — это просто рёбра, что упрощает тот же самый запрос.
PREFIX mv: <your_movie_ontology_URL>
SELECT ?person ?role
WHERE {
?person ?role mv:casablanca.
}В Cypher есть схожая конструкция. GQL также могут управлять рёбрами: разворачивать их, комбинировать, использовать транзитивное замыкание и прочее. Если нам понадобится найти всех актёров так или иначе связанных с Кевином Бейконом цепочкой фильмов, то можно написать:
PREFIX mv: <your_movie_ontology_URL>
SELECT ?a
WHERE {
mv:kbacon (:acted_in/^:acted_in)+ ?a.
# a/b = объединить два поиска
# ^a = развернуть a
# a+ = транзитивное замыкание
}SPARQL не может сообщить нам длину пути или вычисления вдоль этого пути, такие как построение цепочки фильмов, связывающих двух актёров. GQL с поддержкой таких возможностей намного сложнее.
Ознакомившись с различными GQL, я пришёл к выводу, что есть набор полезных примитивов для обхода, которые процедурный язык с поддержкой графов должен предоставлять. Интересно, что в официальном языке спецификаций Alloy, оперирующим типом данных «отношение» (relation), все эти примитивы есть. По этой причине для меня работать с графовым представлением в Alloy намного проще, чем в типичном языке программирования. Тем не менее все они работают с размеченными рёбрами и могут не работать для других представлений графов.
▍ Передовые языки с поддержкой графов в стандартной библиотеке
В 2020 году в Python добавили graphlib. Судя по этой дискуссии, причиной стало то, что топологическая сортировка является «фундаментальным алгоритмом» и будет полезной для «чистых реализаций логики MRO (Method Resolution Order, порядок разрешения методов)». В Graphlib есть только метод TopologicalSorter, который получает графы, представленные в виде словарей узлов. Немного необычно, но этот словарь узлов имеет обратное направление: граф a -> b представляется в нём как {b: [a]}.
На конец 2023 года в CPython graphlib никак не используется, и на GitHub на эту библиотеку ссылается менее 900 файлов. К сравнению, другой добавленный в 2020 году пакет — zoneinfo — встречается более, чем в 6,000 файлов, а выражение def topological_sort( — в 4,000. Хотя, я думаю, что многие из них появились до 2020 года. В результате беглого просмотра я заметил, что все эти кастомные топологические сортировки используют иные графовые представления, нежели graphlib, так что преобразовать их не выйдет. Представление графа важно.
Мне удалось найти ещё два языка с поддержкой графов: Erlang и SWI-Prolog. Я не знаю ни тот ни другой, поэтому не могу сказать, почему их в них добавили. По крайней мере, в случае Erlang это произошло до 2008 года. Я отписал человеку из комитета по этому языку, но он мне не ответил.
▍ Графовые языки
Это языки программирования, в которых «всё является графом» также, как в bash всё является строкой, а в lisp — списком. Из примеров могу назвать GP2 и Grape. Пообщавшись со специалистами из этой сферы, я понял, что она всё ещё находится преимущественно в академическом русле.
▍ Языки для работы с математикой
Mathematica, MATLAB, Maple и так далее все содержат графовые библиотеки в той или иной форме. Но я не готов платить тысячи долларов за лицензии, необходимые, чтобы разобраться в этом подробнее.
▍ Сноски
1. Серьёзно. Хэш-таблицы являются двухдольными графами. Этот принцип использовался при доказательстве быстродействия алгоритма «хэширование кукушки». ↪
2. Оба вычисления я получил с помощью cloc 1.96. Я выполнил cloc в networkx/networkx/algorithms (56989) и в cpython/Lib (588167). Вся библиотека NetworkX составляет ~90,000 строк кода. ↪
3. Вы можете повысить эффективность за счёт сохранения упорядоченности списка рёбер и выполнения двоичного поиска O(log(|e|)) ценой удорожания операции добавления рёбер. ↪
4. NetworkX содержит функции для преобразования графов в другие представления, но не для работы с этими представлениями напрямую. ↪
5. 14 из 21 традиционных NP-полных задач являются задачами на графах. ↪
6. Не путайте с языком GQL, предложенным в качестве стандарта GQL, который всё ещё находится в разработке. ↪
Автор: Дмитрий Брайт