
Статья посвящена знакомству с инструментом micrograd и компиляции генерируемых им нейронных сетей в язык С. При этом она не является руководством по машинному обучению, но вполне может позволить вам лучше понять МО через призму компиляторов. В ходе этого процесса мы также разберём цепное правило, напишем собственный небольшой компилятор и посмотрим, как micrograd масштабируется.
Недавно у меня состоялся приятный разговор с моим другом Крисом. Он познакомил меня с основами машинного обучения, когда я разбирал написанный Андреем Карпаты micrograd.
Для тех, кто не знает, micrograd – это небольшая реализация нейронной сети, написанная на чистом Python без библиотек, в которой вычислительными единицами выступают не векторы и матрицы, а скалярные величины.
Micrograd представляет из себя комбинацию нескольких взаимодополняющих частей:
- небольшого построителя и оценщика выражений на основе графа;
- автоматической дифференциации в обратном режиме для того же самого графа вычислений;
- строительных блоков нейронной сети для многослойного перцептрона (MLP, Multy-Layer Perceptron).
Если вы не знаете, что такое MLP, не волнуйтесь. Эта статья познакомит вас с общими понятиями, особенно если вы уже уверенно используете Python. Возможно, перед началом вам стоит почитать и проанализировать исходный код micrograd, а также взглянуть на это интерактивное руководство. Хотя, может, и нет. Тут решать вам. Экспериментирование с micrograd лично мне хорошо помогло. Крис предложил попробовать заставить сеть выучить XOR.
Все вместе эти три основных компонента позволяют писать такой код:
from micrograd.nn import MLP
model = MLP(2, [4, 1])И призывать нейронную сеть из воздуха.
Когда я впервые его прочёл, то меня привлёк один момент. Раньше я считал, что строительные блоки являются сетью. В данной же библиотеке это не так. Если использовать аналогию со строительством, то они больше похожи на схемы. С каждой оценкой сети связующее звено (промежуточный вычислительный граф) строится заново. С позиции компилятора строительные блоки подобны фронтенду, а граф – промежуточному представлению (IR, Intermediate Representation).
Вам может быть интересно, почему я об этом рассказываю. Обычно я пишу о компиляторах. Что же случилось?
Дело в том, что когда я разобрался в этих трёх компонентах micrograd, то понял:
- модели МО – это графы;
- прямой и обратный проходы – это обходы графа;
- структура графа не изменяется со временем;
- производительность важна.
Всё это звучит как отличная возможность для компиляции! Именно поэтому проекты вроде PyTorch и TensorFlow содержат компиляторы (TorchScript/TorchDynamo/AOT Autograd/PrimTorch/TorchInductor/Glow, XLA и так далее). Компиляция модели ускоряет и обучение, и вывод. Поэтому текущая статья не будет содержать чего-то нового – надеюсь, она станет быстрым наброском небольшого примера того, что делают крупные проекты.
Здесь мы будем компилировать нейронные сети micrograd в С. Для этого мы:
- вкратце познакомимся с нейронными сетями;
- рассмотрим, как micrograd выполняет прямой и обратный проход;
- разберём правило цепи;
- узнаем причину медлительности micrograd;
- напишем небольшой компилятор;
- посмотрим, как micrograd масштабируется;
Приступим!
Как micrograd создаёт нейронные сети
Сначала немного поговорим о многослойных перцептронах. MLP – это плотно связанные нейронные сети, в которых входные данные протекают через сеть в одном направлении. Поскольку micrograd находится в вышестоящем репозитории, то поддерживает только MLP.
Для лучшего усвоения информации приведу наглядную схему:
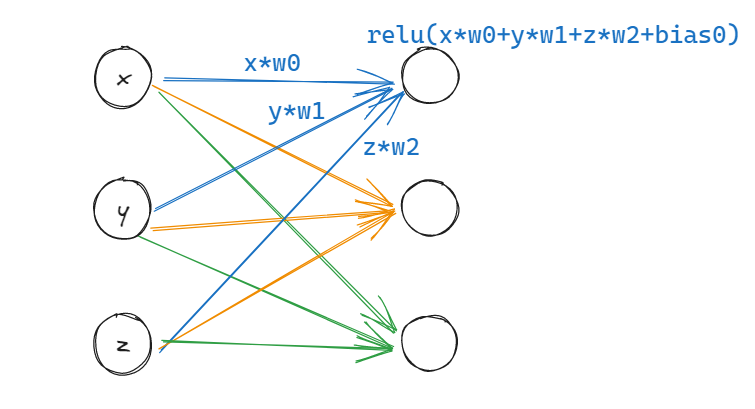
Рис. 1. Схема многослойного перцептрона, правда, слой всего один. Я построил её в Excalidraw. Мне нравится Excalidraw.
На этом изображении кружки представляют данные (ввод или промежуточные результаты вычислений), а стрелки – веса и операции с данными. В этом случае круги x, y и z являются входными данными. Стрелки, направленные вправо, представляют умножение на веса. Встреча стрелок означает сложение (формирующее скалярное произведение), за которым следует прибавление смещения (аналог весов). Всё это передаётся в функцию активации (в данном случае ReLU, rectified linear unit, блок линейной ректификации)1. Круги справа являются результатами прохождения первого слоя.
Карпаты реализует это прямо – у него каждый нейрон является экземпляром класса Neuron и содержит метод __call__, дающий скалярное произведение. После этого каждое произведение оказывается в функции активации, в данном случае ReLU, которая равнозначна max(x, 0). Я думаю, что 0 является произвольным порогом, но не уверен.
Ниже приводится весь код MLP в micrograd (мы вернёмся к классу Value позже):
import random
from micrograd.engine import Value
class Module:
def zero_grad(self):
for p in self.parameters():
p.grad = 0
def parameters(self):
return []
class Neuron(Module):
def __init__(self, nin, nonlin=True):
self.w = [Value(random.uniform(-1,1)) for _ in range(nin)]
self.b = Value(0)
self.nonlin = nonlin
def __call__(self, x):
act = sum((wi*xi for wi,xi in zip(self.w, x)), self.b)
return act.relu() if self.nonlin else act
def parameters(self):
return self.w + [self.b]
def __repr__(self):
return f"{'ReLU' if self.nonlin else 'Linear'}Neuron({len(self.w)})"
class Layer(Module):
def __init__(self, nin, nout, **kwargs):
self.neurons = [Neuron(nin, **kwargs) for _ in range(nout)]
def __call__(self, x):
out = [n(x) for n in self.neurons]
return out[0] if len(out) == 1 else out
def parameters(self):
return [p for n in self.neurons for p in n.parameters()]
def __repr__(self):
return f"Layer of [{', '.join(str(n) for n in self.neurons)}]"
class MLP(Module):
def __init__(self, nin, nouts):
sz = [nin] + nouts
self.layers = [Layer(sz[i], sz[i+1], nonlin=i!=len(nouts)-1) for i in range(len(nouts))]
def __call__(self, x):
for layer in self.layers:
x = layer(x)
return x
def parameters(self):
return [p for layer in self.layers for p in layer.parameters()]
def __repr__(self):
return f"MLP of [{', '.join(str(layer) for layer in self.layers)}]"
Можете проигнорировать некоторые хитроумные части MLP.__init__. Она обеспечивает соответствие размерности всех слоёв, а также линейность последнего слоя, которая означает, что к нейронам не прикреплена функция активации.
Но эта сеть построена не только с помощью чисел с плавающей запятой. Вместо этого Карпаты использует некую Value. Что это такое?
Знакомство с построителем выражений
Выше я сказал, что одним из компонентов micrograd является построитель графов выражений.
Его использование выглядит как несколько усложнённый способ выполнения математических действий на Python:
>>> from micrograd.engine import Value
>>> a = Value(2)
>>> b = Value(3)
>>> c = Value(4)
>>> d = (a + b) * c
>>> d
Value(data=20, grad=0)
>>>
Класс Value даже реализует все методы операторов вроде __add__, чтобы облегчить процесс и сделать его максимально похожим на математические операции в Python.
Но при этом он немного отличается от стандартной математики. Причина отличий в том, что, во-первых, в нём есть поле grad – о котором мы поговорим позже – а также в том, что при выполнении вычислений он также строит граф (можете представить его как абстрактное синтаксическое дерево, или AST).
Хотя в обычном строковом представлении он не виден. Экземпляры Value содержат скрытое поле _prev, в котором хранятся составляющие выражения:
>>> d._prev
{Value(data=5, grad=0), Value(data=4, grad=0)}
>>>
В них также есть скрытое поле оператора:
>>> d._op
'*'
>>>
Это означает, что у нас есть два операнда для узла d: c (4) и a + b (5).
Я сказал, что вы можете представить класс Value как AST, но это не совсем AST, поскольку он не является деревом. Это ожидаемо и для него вполне нормально иметь структуру, больше походящую на направленный ациклический граф (DAG, Directed Acyclic Graph).
>>> w = Value(2)
>>> x = 1 + w
>>> y = 3 * w
>>> z = x + y
>>> z
Value(data=9, grad=0)
>>>
Здесь x и y используют w, а затем обе используются z, формируя узор в виде ромба.
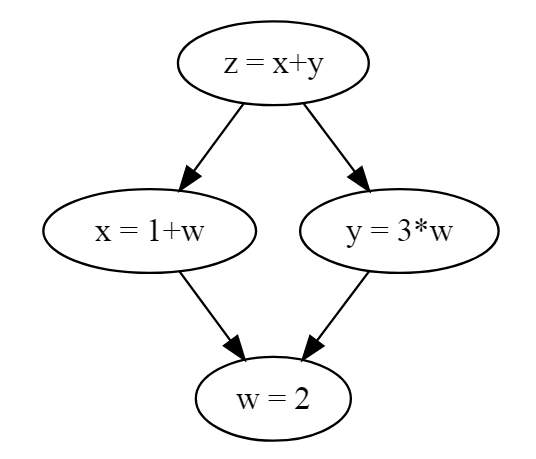
Рис. 2 – граф зависимостей, который содержит зависимости в форме ромба, что делает его направленным графом, а не деревом.
Предполагается, что граф не будет содержать циклы2.
Как же будет выглядеть создание графа в коде? Что ж, функция Value.__mul__, вызываемая для левой стороны операции x*y3, выглядит так:
class Value:
# ...
def __mul__(self, other):
# создаём переходное значение, если правая часть равна постоянному # целому числу или числу с плавающей запятой, например, v * 3
other = other if isinstance(other, Value) else Value(other)
# передаём новые данные, потомков и операцию
out = Value(self.data * other.data, (self, other), '*')
# ... мы вернёмся к этой скрытой части позднее ...
return out
Кортеж потомков (self, other) представляет указатели на другие узлы в графе.
Но зачем нам все эти графы выражений? Почему бы не использовать простую математику? Кому нужны эти обратные указатели?
Поговорим о grad(иенте)
Обучение нейронной сети – это процесс формирования функции (нейронной сети) во времени для вывода желаемых результатов. Внутри функции находится множество коэффициентов (весов), которые при обучении итеративно корректируются.
Стандартный процесс обучения включает структуру вашей нейронной сети, а также другую функцию, которая сообщает, насколько далёк ваш вывод от ожидаемого значения (функции потерь). Простым примером функции потерь будет loss(actual, expected) = (expected - actual)**2 (где ** является операцией Python по возведению в степень). Если вы используете эту функцию для множества входных данных одновременно, то она будет называться функцией вычисления среднеквадратичной ошибкой (MSE, Mean Squared Error)4.
Если вы пытаетесь получить ожидаемый вывод, то вам нужно максимально минимизировать значение функции потерь через обновление весов.
Чтобы понять, какие веса нужно обновлять и насколько, необходимо знать, в какой степени каждый из них воздействует на итоговые потери. Не все веса равны. Некоторые оказывают значительно большее влияние, чем другие.
Ответ на вопрос «В какой степени этот вес воздействовал на потери в этом раунде?» даётся посредством значения grad (градиента) этого веса—первой производной—уклона в определённой точке. Например, в уравнении y = mx + b, которое описывает линию, производной относительно x будет m, поскольку значение x масштабируется на m (а b постоянно).
Для вычисления градиента нужно пройти в обратном направлении от значения потерь5, чтобы выполнить так называемую автоматическую дифференциацию в обратном режиме (AD в обратном режиме). Звучит пугающе. Все статьи онлайн, где она описывается, содержат кажущуюся сложной нотацию и волнистые линии. Но на деле пугаться нечего, так что продолжайте читать.
К счастью для нас, AD в обратном режиме, как и оценка AST сверху вниз, является операцией обхода графа с неким локальным состоянием. Если вы можете написать интерпретатор обхода дерева, то можете выполнить автоматическую дифференциацию в обратном режиме.
▍ AD в обратном режиме и обратное распространение ошибки
Вместо построения параллельного графа производных (в некоем смысле «дуального» для нормального графа выражений), AD в обратном режиме вычисляет локальные производные в каждом узле поля grad. Затем вы можете распространить эти градиенты обратно по графу от значения потерь до весов, что и называется обратным распространением ошибки.
Но как составить все эти локальные производные? Есть ли тут лёгкий способ? Получение производных больших математических выражений пугает…
На деле же в математическом анализе уже есть ответ в так называемом цепном правиле.
Цепное правило
Я не стану прикидываться математиком. Помимо материала, изученного за последние пару недель, я лишь смутно припоминаю цепное правило, с которым познакомился 10 лет назад. Из тех времён я лишь помню, что моя подруга Джулия разобралась в нём мгновенно и удивлялась, почему я не догоняю. Вот, собственно, и всё. Так что, если этот раздел окажется для вас недостаточно понятным, то советую поискать описание этого правила где-нибудь ещё.
▍ Краткий обзор
Цепное правило описывает, как вычислять производные композиции функций. Например, возьмём пример из Wikipedia. Если у вас есть функция h(x) = f(g(x)), то h'(x) = f'(g(x)) * g'(x) (где f', h' и g' являются производными f, h и g соответственно). Это красивое правило, поскольку вам не приходится ухищряться, когда вы начинаете компоновать функции. Главное понимать, как получать производную каждой составляющей части.
Например, если у вас есть sin(x**2), то для получения ответа, cos(x**2) * 2x, вам достаточно узнать производную компонентных функций x**2 (это 2*x) и sin(x) (это cos(x)).
Чтобы познакомиться с этим процессом наглядно и попрактиковать, загляните в эту короткую презентацию в PDF, сделанную Обернским университетом. В оглавлении страницы курса можно найти и другие презентации6.
Также ознакомьтесь со списком правил дифференциации в Wikipedia.
Оказывается, что цепное правило помогает при получении производных потенциально огромных графов выражений. Никому не нужно сидеть и усердно трудиться, чтобы получить производную вашей громоздкой и, без сомнений, излишне сложной функции… У вас просто есть уже знакомые составляющие блоки, которые вы компонуете.
Теперь применим цепное правило к графам выражений.
▍ Применение к графу
Начнём с одного узла Value. Для заданного узла мы можем проделать один шаг цепного правила (в псевдокоде):
# псевдокод
def backward(node):
for child in node._prev:
child.grad += derivative_wrt_child(child) * node.grad
Здесь wrt означает «относительно». Важно получать производную каждого потомка относительно этого потомка.
Вместо того, чтобы просто установить child.grad, есть две причины, по которой мы его увеличиваем:
- один потомок может иметь и других родителей, в случае чего он влияет на обоих;
- группирование, но сейчас это не важно.
Чтобы внести конкретику, взглянем на реализацию Карпаты производной *. В математике, если у вас есть f(x,y) = x*y, тогда f'(x, y) = 1*y (относительно x), а f'(x, y) = x*1 (относительно y). В коде это выглядит так:
class Value:
# ...
def __mul__(self, other):
other = other if isinstance(other, Value) else Value(other)
out = Value(self.data * other.data, (self, other), '*')
# Недостающий фрагмент из кода ранее!
def _backward():
self.grad += other.data * out.grad
other.grad += self.data * out.grad
out._backward = _backward
return out
Это означает, что для каждого из потомков мы будем использовать данные другого потомка (согласно цепному правилу) и умножать их на grad родительского выражения. Это значит, что градиент self (левая сторона) корректируется с помощью данных other (правая сторона) и наоборот. Видите, какой получается красивый перевод математических операций? Получаем производную, применяем цепное правило, прибавляем к градиенту потомка.
Теперь у нас есть функция для выполнения одного производного шага для одного узла операции, а нам нужно обойти весь граф.
Но обойти граф не так просто, как обойти дерево. Вам нужно избегать посещения узла более одного раза, а также обеспечить посещение дочерних узлов до родительских (в прямом режиме) или родительских до дочерних (в обратном режиме). Нюанс в том, что хоть мы и не посещаем узел более одного раза, посещение обновляет потомков узлов (не сам узел), а узлы могут иметь общих потомков, в случае чего grad потомков будет обновляться несколько раз. Это ожидаемое и вполне нормальное поведение.
По этой причине мы используем топологическую сортировку.
Топологическая сортировка и трансформации графа
Топологическая сортировка графа – это порядок, в котором потоки всегда посещаются до своих родителей. Как правило, это работает, только если граф не содержит циклы – но, к счастью, выше мы уже утвердили, что в графе нет циклов.
Вот пример топологической сортировки графа Value. В ней для лаконичности используется вложенная функция build_topo, но это не является строго обязательным.
class Value:
# ...
def topo(self):
# изменён из Value.backward, которая внутренне создаёт топологическую сортировку
topo = []
visited = set()
def build_topo(v):
if v not in visited:
visited.add(v)
for child in v._prev:
build_topo(child)
topo.append(v)
build_topo(self)
return topo
Чтобы лучше понять, как это работает, можно выполнить топологическую сортировку для очень простого графа выражений, 1*2.
>>> from micrograd.engine import Value
>>> x = Value(1)
>>> y = Value(2)
>>> z = x * y
>>> z.topo()
[Value(data=1, grad=0), Value(data=2, grad=0), Value(data=3, grad=0)]
>>>
Здесь сортировка говорит, что для вычисления значения 3 необходимо сначала вычислить значения 1 и 2. Неважно, в каком порядке мы получим1 и 2, главное они оба должны идти до 3.
Теперь, когда мы можем получить порядок обхода графа, можно заняться обратным распространением.
Обратное распространение
Если сейчас мы возьмём то, что знаем о цепном правиле и топологической сортировке, то сможем выполнить для графа операцию обратного распространения. Ниже приведён код прямо из micrograd. Он сначала выполняет топологическую сортировку, а затем обрабатывает упорядоченные узлы в обратном порядке, применяя цепное правило к каждому Value поочерёдно.
class Value:
# ...
def backward(self):
# топологическое упорядочивание всех потомков в графе
topo = []
visited = set()
def build_topo(v):
if v not in visited:
visited.add(v)
for child in v._prev:
build_topo(child)
topo.append(v)
build_topo(self)
# --- новая часть ---
# перебор по одной переменной и применение цепного правила для получения её градиента
self.grad = 1
for v in reversed(topo):
v._backward()
Функция Value.backward обычно вызывается для результата Value функции потерь.
Если вам интересно, почему здесь мы перед выполнением обратного распространения устанавливаем self.grad на 1, то подумайте над этим самостоятельно. Нелишним будет нарисовать картинку.
Объединение всего
Я не собираюсь углубляться в детали, но покажу, как может выглядеть примерный набросок очень упрощённого обучающего цикла для MLP-классификатора в задаче распознавания цифр базы данных MNIST. Этот код нельзя выполнить в его текущем виде. Ему требуется код для загрузки изображений и функция потерь. Гиперпараметры (размер пакета и так далее) здесь полностью произвольны и не настроены. Весь обучающий код и соответствующие модификации движка для добавления exp/log/Max доступны в репозитории GitHub.
import random
from micrograd.nn import MLP
# ...
NUM_DIGITS = 10
LEARNING_RATE = 0.1
# Каждое изображение имеет размер 28x28. Скрытый слой имеет толщину 50. Выводятся 10 цифр.
model = MLP(28*28, [50, NUM_DIGITS])
# Представим, что есть некая функция, загружающая размеченные обучающие изображения в память.
db = list(images("train-images-idx3-ubyte", "train-labels-idx1-ubyte"))
num_epochs = 100
for epoch in range(num_epochs):
for image in db:
# Нулевой градиент
for p in model.parameters():
p.grad = 0.0
# Прямой проход
output = model(image.pixels)
loss = compute_loss(output)
# Обратный проход
loss.backward()
# Обновление
for p in model.parameters():
p.data -= LEARNING_RATE * p.grad
В этом фрагменте построение MLP (model = MLP(...)) создаёт множество Neuron в Layer и инициализирует веса в виде Value, но граф пока не строит. Только при вызове (как в model(image.pixels)) она создаёт граф и выполняет все операции скалярного умножения. Затем поверх этого графа мы строим дополнительный, когда вычисляем потери. Это прямой проход!
Вот диаграмма, которую я сделал, чтобы можно было объяснять другим «добавление потерь сверху»:
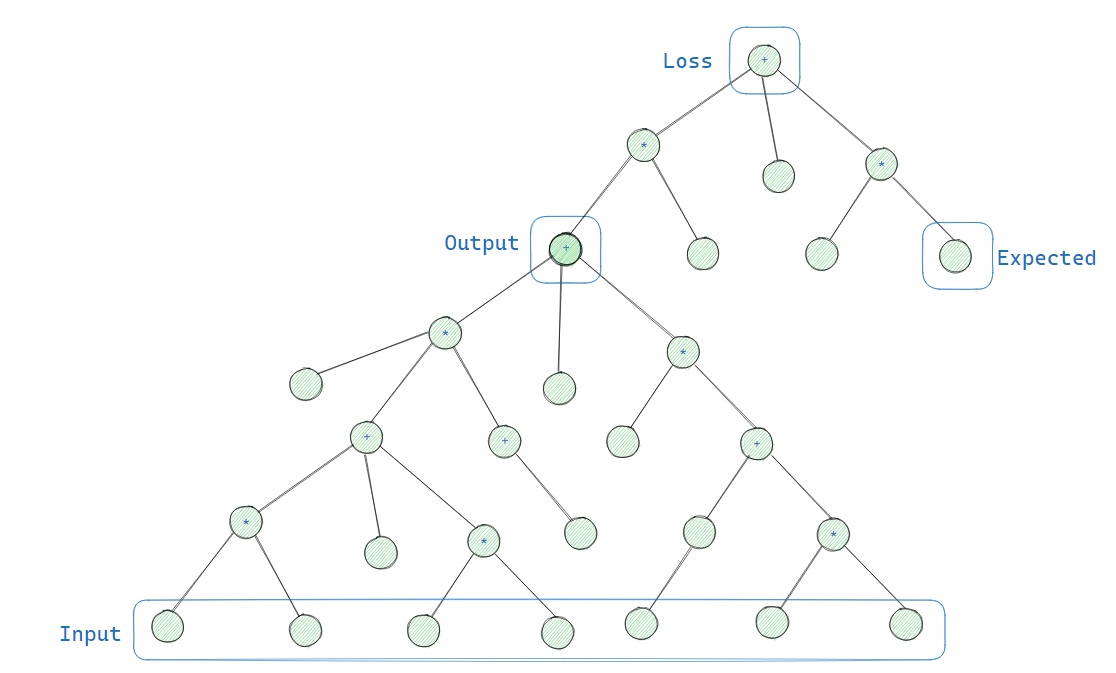
Рис. 3 Иллюстрация графа вычислений и потерь модели. Выводом этой модели будет одно значение, но откуда нам знать, насколько оно точно? Что ж, мы передали его в другой подграф – функцию потерь – которая получает второй ввод (ожидаемое значение) и сама выводит одно значение. Нарисовал я этот граф в Excalidraw.
Затем у нас идёт обратный проход, где мы вызываем backward() для потерь, как я объяснял выше.
Далее мы корректируем все веса по их градиентам.
Не забывайте обнулять свои градиенты!

Перевод:
Наиболее распространённые ошибки сетей: 1) вы не попробовали сначала переобучить одну ветку; 2) вы забыли переключить режим обучение/оценка; 3) вы забыли выполнить
zero_grad()(в pytorch) перед.backward(); 4) вы передали выводы softmax в функцию потерь, которая ожидает необработанные логиты; ещё варианты?
Всё это красиво и просто – спасибо вам, Андрей – но достаточно ли быстра эта модель для эффективного использования? Сейчас выясним.
Проблемы производительности
Мда, с помощью CPython выполняется этот код медленно. Похоже, что вычисление прямого прохода для одного изображения занимает около секунды. А затем нам нужно ещё и пройти обратно. При этом всего необходимо прогнать через несколько эпох обработки аж 60,000 изображений. Это займёт слишком много времени.
Что ж, давайте сделаем то, что обычно в таких случаях предлагают: попробуем PyPy. Да уж, пара изображений в секунду, всё равно недостаточно быстро.
Кстати, наш старый проект Skybison здесь сработает намного быстрее, чем CPython и PyPy! Забавно. После некоторого профилирования его основной проблемой производительности было создание функции (сейчас в Skybison оно работает медленно), но если поднять внутренние функции _backward на верхний уровень, эта проблема исчезнет. Затем становится очевидно, что самой медленной частью профиля является поиск множества из топологической сортировки. После этого идёт сбор мусора со всех временных объектов.
Периодическое поднятие внутренних функций на верхний уровень также значительно ускоряет PyPy, который начинает обгонять Skybison.
Если бы я пытался угадать, то в качестве причин проблем быстродействия предположил бы:
- воссоздание графа при каждом прямом проходе, в результате чего происходит излишнее выделение
Valueи всех их функций_backward.- также наблюдаются большие издержки при выполнении большого числа выделений и итерации в
zipизNeuron.__call__;
- также наблюдаются большие издержки при выполнении большого числа выделений и итерации в
- выполнение топологической сортировки при каждом обратном проходе, включающей погоню за указателями, вызовы функций, а также выделение
set/listи операции; - обычные издержки интерпретатора Python.
Если я что и усвоил за долгие годы, так это то, что вместо слепой оптимизации сначала нужно проводить измерения.
▍ Сверка с профилировщиком
Эмери Бергер со своей командой выпустили прекрасный инструмент Python под называнием Scalene. Для его использования вместо python3 progam.py нужно выполнить scalene yourprogram.py, и когда он закончит (или вы нажмёте Ctrl+C), появится небольшой локальный сайт с информацией о профиле программы.
Я выполнил Scalene для нашего небольшой БД MNIST в micrograd, и вот, что получил на выходе:
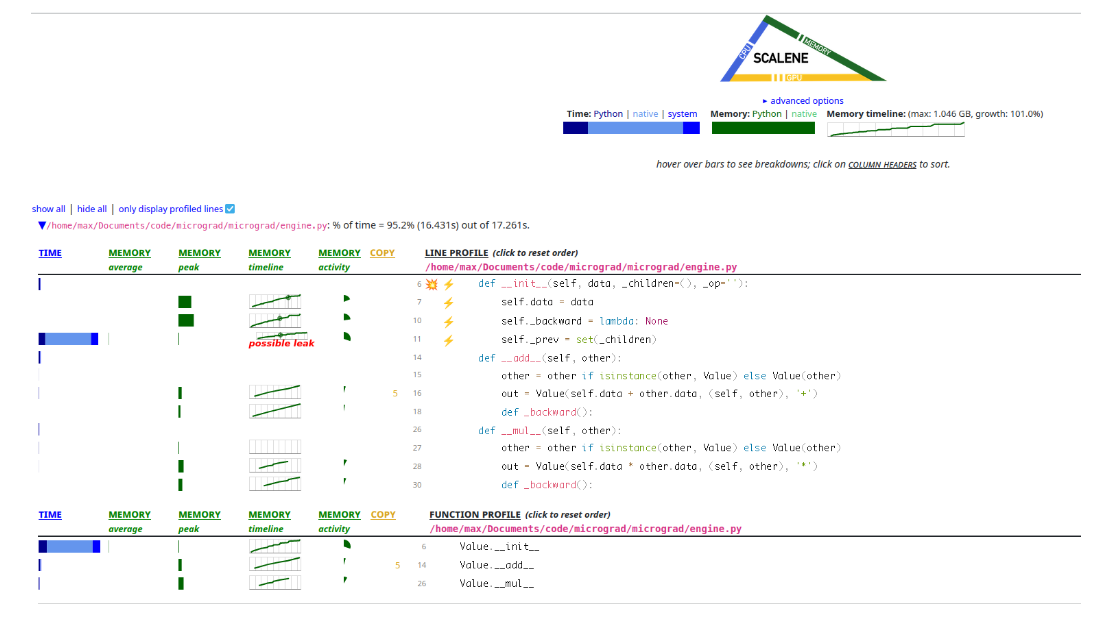
Рис. 4 Скриншот вывода Scalene для micrograd. Похоже, здесь присутствует много выделений Value, а устанавливаемая self._prev даже может оказаться утечкой! В частности, здесь видно много операций + и *, потому что __add__ и __mul__ часто выделяют память.
Похоже, в столбце памяти линия идёт вверх и вправо, что нам не нужно. Также видно, что очень много времени уходит на создание set элементов _prev для каждого Value.
Если вы старой закалки и не доверяете профилировщикам, то можете подтвердить эти наблюдения с помощью perf. Нужно будет установить отладочные символы для вашего дистрибутива Python (в моём случае это был python3.10-dbg для Ubuntu), после чего вы сможете выполнить perf record python3 yourprogram.py. Вот, как выглядит это представление у меня (срез ниже 0.5%):
Samples: 138K of event 'cpu_core/cycles/', Event count (approx.): 64926188565
Overhead Command Shared Object Symbol
37.41% python3 python3.10 [.] gc_collect_main.lto_priv.0
27.85% python3 python3.10 [.] deduce_unreachable
9.91% python3 python3.10 [.] visit_reachable.lto_priv.0
3.58% python3 python3.10 [.] set_traverse.lto_priv.0
3.29% python3 python3.10 [.] dict_traverse.lto_priv.0
2.65% python3 python3.10 [.] _PyEval_EvalFrameDefault
2.04% python3 python3.10 [.] func_traverse.lto_priv.0
1.67% python3 python3.10 [.] subtype_traverse.lto_priv.0
1.16% python3 python3.10 [.] tupletraverse.lto_priv.0
0.73% python3 python3.10 [.] _PyObject_GenericSetAttrWithDict
0.54% python3 python3.10 [.] cell_traverse.lto_priv.0
0.52% python3 python3.10 [.] insertdict.lto_priv.0
gc_collect_main, занимающая 37% профиля, можно назвать большим красным флагом. Последующие функции ниже (deduce_unreachable и все функции _traverse) также, похоже, связаны с GC… Это значит, что программа просто тонет в операциях выделения памяти. Так что Scalene и perf согласуются.
Если вы удалите set(_children) и просто оставите его как кортеж (это не должно повлиять на корректность), то профиль получится чуть более расширенным.
Ещё одно простое исправление состоит в добавлении __slots__ в класс Value. Словари атрибутов, похоже, являются единственным местом, где мы выделяем словари, так что этот момент можно проработать. После добавления __slots__ инструкция dict_traverse определённо исчезнет.
И последнее, мы можем также попробовать удалить операции выделения вложенных функций (как мы пробовали выше для Skybison/PyPy), что также приведёт к удалению func_traverse. Хотя это потребует чуть больше работы, чем предыдущие микрооптимизации.
И ни одно из этих мелких исправлений не меняет общую архитектуру программы, которая включает очень много работы для выполнения небольшого объёма математики и обхода графа7.
Что же делать?
▍ Решения
Как мне нравится говорить, лучший способ ускорить программу – это сократить объём её работы. Слишком много GC? Меньше выделений. Слишком много рекурсии? Уменьшаем топологическую сортировку. Слишком высокие издержки? Меньше интерпретируем. Если конкретно, то здесь я предлагаю:
- Повторно использовать структуру графа между входами. Вместо построения графа
Valueкаждый раз заново, копировать в него новые входные данные и распространять их вперёд/назад. - Поскольку вы больше не меняете граф, повторно выполнять сортировку тоже не нужно. Сохраняйте полученный порядок. Это поможет как при прямом, так и при обратном проходе.
- В конечном итоге абстракция
Valueне имеет большого значения. Если мы знаем, в каком порядке нужно обходить граф, и используем числа двойной точности IEEE-754, то должны компилировать топологическую сортировку с её операциями в С или во что-то более низкоуровневое8.
Это согласуется с тем, что нам уже известно о компиляторах: если вы можете заморозить некий динамизм в допустимой семантике программы, то получите прирост производительности.
Поскольку форма графа статична, это кажется хорошей идеей.
Напишем компилятор
Нашей целью будет написать нечто совсем небольшое, что адекватно впишется в micrograd в его текущем виде – без перестройки.
Мы можем написать компилятор в форме байткода. Это избавит нас от всех вызовов функций, повторяющихся обходов деревьев и погони за указателями. Пожалуй, так он получится быстрее. Но, к сожалению, нам по-прежнему придётся интерпретировать цикл, и этот интерпретатор будет написан на Python, причём наложит значительные издержки.
Вместо этого мы пойдём дальше и скомпилируем этот линейный код в С. Конечной целью будет сделать расширение Python C, которое мы сможем импортировать и использовать вместо интерпретированной версии micrograd.
Исходная версия проекта компилировала классы MLP, Layer и Neuron непосредственно в C, но, к сожалению, это не очень расширяемый вариант: внесение архитектурных изменений в модель потребует написания новых компиляторов. Эта версия также не поддерживала обратное распространение, поэтому только помогала в выводе.
По этой причине мы пишем для графов Value компиляторы. Это означает, что любой может свободно получить такой компилятор, если в его архитектуре машинного обучения используются Value. Для этого лишь нужно написать интерпретатор!
▍ Прямой проход
Поскольку у нас есть топологическая сортировка, мы также можем применять её как вперёд, так и назад. Тогда нам нужно лишь написать компилятор, обрабатывающий по одному Value одновременно. Реализовать его можно так:
>>> from micrograd.engine import Value
>>> x = Value(1)
>>> y = Value(2)
>>> z = x * y
>>> order = z.topo()
>>> for v in order:
... print(v.compile())
...
data[1] = 2;
data[0] = 1;
data[2] = data[1]*data[0];
>>>
(Где предполагается, что data – это некий массив правильного размера со значениями double, которые мы создадим позднее.)
А вот и она! Небольшая опрятная линеаризация графа. Она подобна топологической сортировке, но в коде С. Эта стратегия работает, потому что у нас нет циклов и повторных определений Value. Каждое значение устанавливается всего раз9, и этот код, даже со всеми его загрузками памяти и сохранениями, должен быть намного быстрее, чем погоня за указателями и вызовы функций в Python.
Это можно сделать аналогично интерпретированной версии, в которой каждый вид операции имеет собственный метод (__add__, __mul__, etc), но проще представить весь компилятор в одном методе. По этой причине я добавляю функцию compile. Взгляните, например, на реализацию константных значений (op=='') и сложения (op=='+'):
class Value:
# ...
def var(self):
return f"data[{self._id}]"
def set(self, val):
return f"{self.var()} = {val};"
def compile(self):
if self._op in ('weight', 'bias', 'input'):
# Не вычислено; установлено в другом месте
return ""
if self._op == '':
return self.set(f"{self.data}")
if self._op == '*':
c0, c1 = self._prev
return self.set(f"{c0.var()}*{c1.var()}")
raise RuntimeError(f"op {self._op} left as an exercise for the reader")
Остальные операторы не особо отличаются. Посмотрите, сможете ли вы понять, как реализовать ** или exp, например. Обратите внимание, что ** требует либо сохранения дополнительных данных, либо некоего грубого приёма.
Вы можете заметить, что эта стратегия компиляции требует присваивания идентификаторов к Value. Для этого я добавил поле _id, представляющее автоматически инкрементируемый счётчик в функции __init__. Сама реализация здесь не особо важна. Просто помните, что каждый объект Value имеет уникальный _id.
Моя полная версия компилятора для всех операций содержит примерно 40 строк и даже включает некоторые попутные оптимизации. Но этот компилятор выполняет прямой проход. А что насчёт обратного? Нам также нужно ускорить обучение. Обратный проход должен быть намного сложнее, не так ли?
▍ Обратный проход
Фактически его сложность примерно та же. Нам лишь нужно построково перевести функции обратного распространения (все реализации _backward).
Например, мы можем вернуться к обратному распространению для *. Я добавил несколько вспомогательных функций, чтобы сократить код и сделать его больше похожим на интерпретированную версию. Как и в версии с прямым проходом, все операторы находятся в одном методе: backward_compile.
class Value:
# ...
def getgrad(self):
if self._op in ('', 'input'):
raise RuntimeError("Grad for constants and input data not stored")
return f"grad[{self._id}]"
def setgrad(self, val):
if self._op in ('', 'input'):
# Нас не интересует установка градиентов для констант или входных данных.
return []
return [f"{self.getgrad()} += {val};"]
def backward_compile(self):
if not self._prev:
assert self._op in ('', 'weight', 'bias', 'input')
# Nothing to propagate to children.
assert not self._prev
return []
if self._op == '*':
left, right = self._prev
return left.setgrad(f"{right.var()}*{self.getgrad()}") +
right.setgrad(f"{left.var()}*{self.getgrad()}")
raise RuntimeError(f"op {self._op} left as an exercise for the reader")
(Как и в версии с прямым проходом, предположим, что grad – это массив правильной формы со значениями double, которые мы создадим позднее).
Посмотрим, как это работает на практике.
>>> x = Value(1, _op='weight')
>>> y = Value(2, _op='weight')
>>> z = x * y
>>> order = z.topo()
>>> for v in order:
... print(v.backward_compile())
...
[]
[]
['grad[6] += data[7]*grad[8];', 'grad[7] += data[6]*grad[8];']
>>>
Хм, странно. Почему здесь присутствует код обратного распространения для x (grad[6]) и y (grad[7])? Дело в том, что у них нет собственных потомков. Вместо этого они корректируются по родительскому узлу, z(grad[8]). Именно это я имел ввиду ранее, когда говорил, что посещение узла корректирует его потомков.
Полная версия компилятора с обратным проходом занимает около 30 строк. Даже короче первой версии с прямым проходом. Неплохо.
Вы только что написали компилятор. Поздравляю! Серьёзно, самая сложная часть позади. Остальное – это небольшие детали и специфики Python C-API, которые вы при желании можете пропустить. Недостаёт у нас только update, set_input и обёрточного кода, которые уже не так интересны.
▍ Обновление
Выполнив обратный проход (возможно, несколько раз), нам нужно скорректировать веса с помощью их градиентов. Генерация кода для этого будет просто механическим переводом кода Python в код C. Для сравнения приведу интерпретированную версию:
def update(model)
for p in model.parameters():
p.data -= LEARNING_RATE * p.gradОна перебирает параметры модели во время выполнения и корректирует их. В скомпилированной версии, напротив, итерация выполняется во время компиляции, а прямолинейные вычитания при выполнении:
def gen_update(f, model, learning_rate):
for o in model.parameters():
assert o._op in ('weight', 'bias'), repr(o._op)
print(f"data[{o._id}] -= {learning_rate} * {o.getgrad()};", file=f)
# data[0] -= 0.01 * grad[0];
# data[1] -= 0.01 * grad[1];
# data[2] -= 0.01 * grad[2];
# ...
Если исключить assert, то эта версия даже имеет ту же длину, что и её равнозначный аналог на Python.
▍ Установка входных данных
Получение ввода из кода Python в С++ имеет некоторые сложности, когда это не простые типы данных вроде целых чисел и значений с плавающей запятой. В идеале наш сгенерированный код модели МО смог бы разделить память с Python, чтобы избежать копирования с места на место, но это будет непростая реализация10, поэтому мы здесь делаем кое-что попроще.
У нас будет функция set_input, получающая данные о чёрных и белых пикселях в массиве байтов и копирующая каждый пиксель в соответствующий слот массива data. И хотя это довольно медленно в сравнении с, например, не копированием, такое решение определённо не является узким местом в пайплайне.
def gen_set_input(inp):
result = []
for idx, o in enumerate(inp):
result.append(f"data[{o._id}] = buf[{idx}];n")
return "".join(result)
В данном случае inp является массивом входных данных. В отличие от интерпретированной версии micrograd, здесь мы не создаём новые входные Value с каждой итерацией. Это означает, что нам нужно заранее выделять диапазон ID для ввода данных в модель МО и вывода из неё:
NUM_PIXELS = 28*28
NUM_DIGITS = 10
inp = [Value(0, (), "input") for _ in range(NUM_PIXELS)]
exp = [Value(0, (), "input") for _ in range(NUM_DIGITS)]
out = model(inp) # create the compile-time Value graph
loss = compute_loss(out, exp)
gen_set_input(inp)
Заметьте, что поля data или grad каждого узла Value содержат мусорные данные, поскольку inp и exp выбираются произвольно. Тем не менее сгенерированный код С на деле не использует эти значения Python. Всё, что нас интересует – это структура графа, представленная полями _op и _prev.
Чтобы использовать этот код C из Python, придётся создать расширение Python C, используя C-API.
▍ Расширение Python C
Наличие некоторого свободно плавающего кода для обновления массивов data и grad – это здорово, и тут у нас полноценный компилятор, хотя пока неготовый к использованию. Нам нужно обернуть этот код в функции (я назвал их forward, backward, update и set_input) и сделать их доступными для нашей программы драйвера на Python. Мы не хотим, чтобы у нас возникла необходимость полностью переезжать на С.
Основная часть здесь проста (конкретно print("void forward() {") и так далее), но кое-что из этого требует знания внутреннего устройства Python.
Например, вот фрагмент обёрточного кода для функции forward.
PyObject* forward_wrapper(PyObject *module, PyObject *const *args, Py_ssize_t nargs) {
if (nargs != 2) {
PyErr_Format(PyExc_TypeError, "expected 2 args: label, pixels");
return NULL;
}
PyObject* label_obj = args[0];
PyObject* pixels_obj = args[1];
if (!PyLong_CheckExact(label_obj)) {
PyErr_Format(PyExc_TypeError, "expected int");
return NULL;
}
if (!PyBytes_CheckExact(pixels_obj)) {
PyErr_Format(PyExc_TypeError, "expected bytes");
return NULL;
}
if (PyBytes_Size(pixels_obj) != 28*28) {
PyErr_Format(PyExc_TypeError, "expected bytes of size 28*28");
return NULL;
}
// ...
}
Это пример функции fastcall из C-API, указывающий на то, что она получает свои аргументы в массиве. Нам нужно её так и зарегистрировать:
static PyMethodDef nn_methods[] = {
{ "forward", (PyCFunction)forward_wrapper, METH_FASTCALL, "doc goes here" },
// ...
};
И затем сделать импортируемое в Python описание модуля, чтобы при импорте можно было создать объект module:
static struct PyModuleDef nnmodule = {
PyModuleDef_HEAD_INIT,
"nn",
"doc goes here",
-1,
nn_methods,
NULL,
NULL,
NULL,
NULL
};
После этого можно будет создать магическую функцию PyInit_nn. Если нативная инструкция импорта в Python найдёт модуль в .so, где находится функция PyInit_XYZ, то вызовет её для создания объекта модуля.
// Некоторые полезные ключевые слова: "PEP 384" и "PEP 489".
PyObject* PyInit_nn() {
PyObject* m = PyState_FindModule(&nnmodule);
if (m != NULL) {
return m;
}
// ...
return PyModule_Create(&nnmodule);
}Вот, собственно, и всё. Теперь мы можем использовать всю проделанную трудную работу для обучения модели и вывода её результатов.
Помогло? Модель ускорилась?
Это два отдельных вопроса, и производительность не имеет значения, если ваш код выдаёт неверный вывод.
▍ Корректность
Тестирование компиляторов может вызывать сложности. В них есть множество компонентов, и они все должны работать как самостоятельно, так и сообща. К счастью, в данном случае у нас есть очень маленький компилятор с небольшим числом простых операций. В итоге написать модульные тесты для сгенерированного кода С можно без особых проблем.
Также, пожалуй, стоит использовать тесты сравнения для выходных чисел интерпретированной и скомпилированной версий одного и того же кода. Если у них будет одинаковый предел погрешности, можно будет считать компилятор корректным. Хотя я не рекомендую использовать MNIST. Интерпретированная версия слишком медленная, а модульные тесты должны быть быстрыми. Возможно, стоит попробовать XOR.
К счастью, в CPython для значений float используется реализация из хост-системы, поэтому мы получаем то же численное поведение, что и в С, без дополнительных усилий.
▍ Производительность
На моей машине обучение происходит со скоростью от 1 изображения в секунду (интерпретированная версия) до >1000 изображений в секунду (скомпилированная версия). Это как минимум в тысячу раз быстрее, хоть и накладывает некоторые издержки. Вам нужно скомпилировать код С. Если вы используете TCC, очень быстрый компилятор С, то получите адекватное быстродействие. Я наблюдал время компиляции в районе полсекунды и 45 секунд на прохождение эпохи. Если вы используете Clang, значительно более медленный компилятор, то быстродействие будет ещё выше. Взгляните на эту наглядную таблицу сравнений:
| Время компиляции (сек) | Время на эпоху (cек) | Ускорение | |
| Интерпретированная версия | 0 | 60 000 | 1x |
| TCC | 0,5 | 45 | 1333x |
| Clang -O0 | ~30 | 30 | 2 000x |
| Clang -O1 | ~350 | 8 | 7 500x |
В любом случае выигрыш приличный. Я думаю, мы сделали это! Весь код компилятора, а также код его обёртки и обучающий код доступны на GitHub.
Заключение
Нейронные сети представлены статичными графами потока данных, которые выполняются как в прямом, так и в обратном направлении. Это означает, что они подобны интерпретаторам, обходящим деревья. Это также значит, что компиляция дерева до более низкоуровневого представления делает программу быстрее.
В более серьёзном смысле: меня всегда мало интересовало применение МО, поскольку эта технология злонамеренно используется либо для причинения людям вреда (слежка, рекомендательные системы, ограничивающие информационное поле человека и так далее) либо делают ПО хуже (к примеру, несколько крупных компаний недавно испортили свои хронологические ленты новостей).
Я познакомился с машинным обучением и написал этот пост, чтобы понять теорию, которой так увлечены мои друзья. Я заклинаю вас, потенциальный практик МО, использовать ваши навыки во Благо.
Размышления и дополнительное чтиво
Если вам интересно, и у вас есть время, то здесь можно проделать ещё много работы. Возможно, я продолжу эту тему, но не уверен.
▍ Линеаризация, но с использованием Python
Насколько можно ускорить версию Python? Если мы создадим граф и топологическую сортировку единожды и будем каждый раз переустанавливать входные значения, ускорится ли код? Вероятно, да. Использование моих предварительных значений показывает ускорение в ~100-200х в CPython и в ~800x в PyPy. Причём нам даже не пришлось писать компилятор.
▍ Оператор Dot
Если мы знаем, что выполняем скалярное произведение в классе Neuron, а также знаем, что эта операция будет откровенно типичной, то можем также использовать одну большую операцию Dot вместо кучи мелких операций + и *. Это позволит забыть о куче промежуточных узлов как при прямом, так и при обратном проходе (сокращение от ~120k узлов до ~40k), и мы получим такой код:
data[100] = data[0]*data[700]+data[1]*data[701]+data[2]*data[702] // ...
data[101] = data[100]+data[800];
data[102] = relu(data[101]);Это несколько упрощает рассуждение о сгенерированном коде. Должен быть способ указать компилятору, например, что скалярные произведения для слоя можно векторизовать, либо то, что они могут все выполняться параллельно. Это должно дать неплохое ускорение.
К сожалению, это требует внесения изменений в код нейронной сети:
diff --git a/micrograd/nn.py b/micrograd/nn.py
--- a/micrograd/nn.py
+++ b/micrograd/nn.py
@@ -1,5 +1,5 @@
import random
-from micrograd.engine import Value
+from micrograd.engine import Value, Dot
class Module:
@@ -19,7 +19,7 @@ class Neuron(Module):
def __call__(self, x):
assert len(self.w) == len(x), f"input of size {len(x)} with {len(self.w)} weights"
- act = sum((wi*xi for wi,xi in zip(self.w, x)), self.b)
+ act = Dot(self.w, x)+self.b
return act.relu() if self.nonlin else act
def parameters(self):
Код для компиляции узла Dot не так запутан:
def dot(l, r):
return sum(li.data*ri.data for li,ri in zip(l,r))
class Dot(Value):
def __init__(self, left_arr, right_arr):
assert len(left_arr) == len(right_arr)
assert left_arr
super().__init__(dot(left_arr, right_arr), tuple(set(left_arr+right_arr)), 'dot')
self.left_arr = left_arr
self.right_arr = right_arr
def compile(self):
products = (f"{li.var()}*{ri.var()}" for li, ri in zip(self.left_arr, self.right_arr))
return self.set(f"{'+'.join(products)}")
def backward_compile(self):
result = []
for i in range(len(self.left_arr)):
result += self.left_arr[i].setgrad(f"{self.right_arr[i].var()}*{self.getgrad()}")
result += self.right_arr[i].setgrad(f"{self.left_arr[i].var()}*{self.getgrad()}")
return resultВыяснение принципа работы обратного распространения оставлю вам, дорогие читатели, в качестве упражнения. Но результаты получились отличные:
| Время компиляции (сек) | Время на эпоху (сек) | Ускорение | |
| Интерпретированная версия | 0 | 60 000 | 1x |
| TCC | 0,5 | 45 | 1 333x |
| TCC с Dot | 0,2 | 14 | 4 300x |
| Clang -O1 | ~379 | 8 | 7 500x |
| Clang -O1 c Dot | ~330 | 3,5 | 17 000 |
| Clang -O2 -march=native c Dot | ~730 | 3 | 20 000x |
Заметьте, что мы даже получили более короткое время компиляции при использовании TСС и Clang -O1 с Dot. И это реально помогает с предварительными числами PyPy, обеспечивая ускорение до ~3300x. Очень здорово!
▍ Компиляция для обучения и вывод результатов
Сейчас наша стратегия компиляции работает как для обучения, так и для вывода. Это хорошо, поскольку ускоряет обе эти операции в сравнении с прежней версией. Но за это приходится платить: вывод происходит немного медленнее.
Если после обучения вы заморозите веса и сделаете их немутабельность известной, то эффективность возрастёт ещё больше. Сейчас у нас так много загрузок из памяти и сохранений, что компилятору С трудно подтвердить что-либо относительно свойств чисел, когда он пытается выполнить оптимизацию. Он, вероятно, также не позволяет использовать инструкции SIMD. Если мы сможем встроить веса в сгенерированный код С как двойные константы, то наверняка получим намного более эффективный машинный код.
▍ Использование скаляров менее эффективно, чем использование тензоров
Мы смогли удалить значительную часть издержек для имевшейся программы, но общая архитектура не сильно улучшилась. Для этого нам нужно перейти от использования скалярных значений Value к использованию тензорных.
Это подобно программированию на ассемблере (скаляры) в сравнении с более высокоуровневым языком (тензоры). На ассемблере значительно труднее реализовывать оптимизации непосредственно. Если у вас в AST есть семантически более крупные и описательные операции (matmul и прочие), то компилятор сможет лучше вас понять и оптимизировать их.
Это также повышает локальность данных (матрица хранится сжато с развёртыванием по столбцам либо строкам) и мы можем получить векторизованные математические операции вместо миллионов mulsd.
Насколько мне известно, оптимизация реальных чисел в линейной алгебре является активным предметом исследований.
▍ Использование PyPy
PyPy – это просто JIT-компилятор для Python, но он также включает язык программирования общего назначения, называемый RPython. Приятно то, что, если вы пишите интерпретатор на RPython, PyPy преобразует его в трассирующий JIT-компилятор. И тут возникает ряд вопросов:
Что, если бы вы написали micrograd на RPython? Делал бы PyPy эффективный JIT из интерпретатора с перебором дерева… даже, если бы он выделял все узлы AST на лету? Не превысил бы он предел длины трейса?
Что, если сгенерировать код Python или байткод? Для этого даже не нужно писать интерпретатор на RPython, зато требуется написание компилятора для преобразования графов Value в Python (байткод). Смог бы PyPy компилировать такое эффективно?
Сноски
- Предполагается, что функция активации будет имитировать поведение биологических нейронов при получении импульсов или чего-то подобного. Объяснение их необходимости читайте в этой статье. Существуют и другие виды функций активации, например, сигмоида и гиперболический тангенс, но по непонятным мне математическим причинам люди склонны использовать ReLu.
- Очевидно, что даже рекуррентные нейронные сети (RNN, Recurrent Neural Network) копируют и вставляют структуру в промежуточное представление вместо того, чтобы использовать реальную структуру цикла.
- В некотором роде. Это упрощение семантики Python. Если вам интересно, ознакомьтесь с прекрасной статьёй Бретта Кэннона.
- Ещё одним видом функции потерь является функция потерь кросс-энтропии, которая лучше всего подходит для решения задач классификации со множеством классов. Добавление этой функции требует поддержки других фундаментальных операций над
Valueи в компиляторе. - Также существует автоматическая дифференциация с прямым режимом, но я мало о ней знаю, и в ходе своего короткого исследования темы случаев её применения не встречал.
- Примечание. Я никогда не видел подобную навигацию в PDF. Очень интересная.
- Дэниэль Лемир написал отличную статью о мифе, что проблемы производительности в основном находятся в нескольких концентрированных точках.
- Изначально я хотел вручную написать весь пайплайн вплоть до машинного кода. Он бы всё равно оказался достаточно мал с учётом всех деталей, но тогда бы мне пришлось регистрировать выделение памяти. В общем, решил пока этого избежать.
- Это по определению составляет его SSA форму.
- Думаю, что она была бы всё равно длиннее. При нашей структуре массивов
dataиgradнам может потребоваться использовать специальное хранилище для входных данных в компиляторе – считывать из разных глобальных переменных или что-то в этом духе. Если вы используете C-API буфера Python, на деле это может быть не таким уж плохим решением. Пожалуй, я оставлю это вам в качестве упражнения.
Автор: Дмитрий Брайт







