Оптимизируем дерево отрезков, делаем из него куст o_O

Введение

Многие знакомы с алгоритмами дерева отрезков и корневой декомпозицией. Однако, не многие задаются вопросом о том, почему они устроены именно так, как они устроенны, и нельзя ли немного изменив их получить выигрыш во времени работы или памяти. Одно из таких изменений я бы и хотел рассмотреть в этой статье.

Предыстория

Данная история мало конструктивна, нужна скорее для понимания того, откуда возникла идея для оптимизации. Подробно о самом алгоритме и написано ниже.

Относительно недавно, я задался вопросом, как объяснить ученикам, мотивацию структурной организации дерева отрезков. До этого мы рассматривали корневую декомпозицию, для которой подобный вопрос почти не стоит. Делим массив на блоки, обновляем элемент, обновляем значение блока, при подсчёте выигрываем на том. что часть ответа уже посчитана для некоторых блоков в отрезке.

В результате непродолжительных размышлений, было придумано следущее.

Дерево отрезков похоже на корневую декомпозицию, отличие только в том, что мы не разбиваем массив на множество блоков, а на два равных по длине блока. После спускаемся "внутрь" блоков и снова разбиваем надвое. Можно сказать, что получается своеобразная рекурсивная оптимизация.

А дальше в течение пары дней идея переросла в то, что мы можем делать корневые оптимизации с меньшим числом блоков и большей глубиной. Или даже взять дерево отрезков и на каждом уровне разбивать не на два блока, а на произвольное k.

Очевидный вопрос, а даст ли нам этот подход какой-нибудь бонус?

Чисто математически, кажется что ответ - нет. Так как

Стоит отметить, что лучшее k среди действительных чисел это e. (что вполне не сложно показать, используя знания первого курса матана). Но понятно, что на практике, как минимум из-за работы с памятью, может оказаться, что лучшее основание даже близко не лежит к 2 или e...

Постановка задачи

Пусть дан массив из n элементов, и есть два вида операций

• обновление значения элемента на позиции i заданным числом new_value

• найти максимум на отрезке от элемента с индексом L до элемента с индексом R

В дальнейшем будем для удобства называть дерево отрезков - ДО, корневую декомпозицию - корневой, а описанный выше подход РДО/SST (Разделённое дерево отрезков/Splitted Segment Tree).

Реализация

Поговорим о том, как написать описанную выше структуру. Будем использовать стандартную для дерева отрезков структуру, и алгоритм будем писать рекурсивно. Собственно вся разница между SST и ДО состоит в том, у каждой вершины, листов будет не два, а k потомков.

Собственно код на С (подключенным для удобства STL):

struct SST {
    int n;
    int in_size;
    vector<int> tree;
 
    SST(int n, int cnt_split, int resize_value) { //init struct
        this->n = n;
        this->in_size = cnt_split;
        this->tree.resize(resize_value, INT_MIN);
    }
 
    void 
    build(int v, int l, int r, vector<int> &array, int size) { //build struct with elements of array
        if (l + 1 == r && l < (int)array.size()) {
            this->tree[v] = array[l];
        } else if (l < (int)array.size()) {
            for (int i = 1; i <= this->in_size; ++i) {
                build(this->in_size * v + i, //v
                      l + size * (i - 1), l + size * i, //l, r
                      array, size / this->in_size);
                this->tree[v] = max(this->tree[v], this->tree[this->in_size * v + i]);
            }
        }
    }
 
    void
    update_list(int v, int l, int r, int size, int position, int value) {
        if (l + 1 == r) {
            this->tree[v] = value;
        } else {
            int block = (position - l) / size + 1;
            update_list(this->in_size * v + block, //v
                        l + size * (block - 1), l + size * block, //l, r
                        size / this->in_size, position, value);
            this->tree[v] = max(this->tree[v], this->tree[this->in_size * v + block]);
        }
    }
 
    void 
    update(int v, int l, int r, int size, int position, int value) {
        if (l + 1 == r) {
            this->tree[v] = value;
        } else {
            int block = (position - l) / size + 1;
            update(this->in_size * v + block, //v
                   l + size * (block - 1), l + size * block, //l, r
                   size / this->in_size, position, value);
            this->tree[v] = INT_MIN;
            for (int i = 1; i <= this->in_size; ++i) {
                this->tree[v] = max(this->tree[v], this->tree[this->in_size * v + i]);
            }
        }
    }
 
    int 
    get_max(int v, int l, int r, int size, int ql, int qr) {
        if (r <= ql || qr <= l) {
            return INT_MIN;
        } else if (ql <= l && r <= qr) {
            return this->tree[v];
        } else {
            int result = INT_MIN;
            for (int i = 1; i <= this->in_size; i++) {
                result = max(result, 
                             get_max(this->in_size * v + i, //v
                                     l + (i - 1) * size, l + i * size, //l, r
                                     size / this->in_size, ql, qr));
            }
            return result;
        }
    }
};

Пояснять код я не буду, так как я уже отмечал, что это по сути обычное ДО, просто при пересчёте и вычислении ответа, в некоторых случаях, нужно запукаться не от двух сыновей, а от ~k. Так же не буду утверждать, что код написан оптимально (в частности это одна из причин по которой я публикую это, чтобы вы, читатели подсказали на возможные упущения сделанные в процессе анализа этого подхода).

Тестирование

Кроме анализа времени работы, так же следует смотреть на затрачиваемую память, так как это тоже немаловажный аспект.

Для тестирования были написаны решения задачи с использованием дерева отрезков, корневой оптимизации и SST. И скрипт на питоне, который работает с терминалом и анализирует время работы и память. Питон был выбран из-за наличия изученных библиотек для отрисовки графиков.

Весь код, а также данные полученные в результате 10 часового подсчёта на моём ноутбуке выложены тут.

О графиках, которые были построены в результате тестирования.

Каждый тест состаял из 1'200'000 запросов (рандомно сгенерированных единожды, в этом тоже может быть проблема, но если генерировать их каждый раз, то тестирование будет занимать в разы больше чем 10 часов, что я к сожалению не могу себе позволить), а так же из n элементов (n от 1000 до 10'000'000).

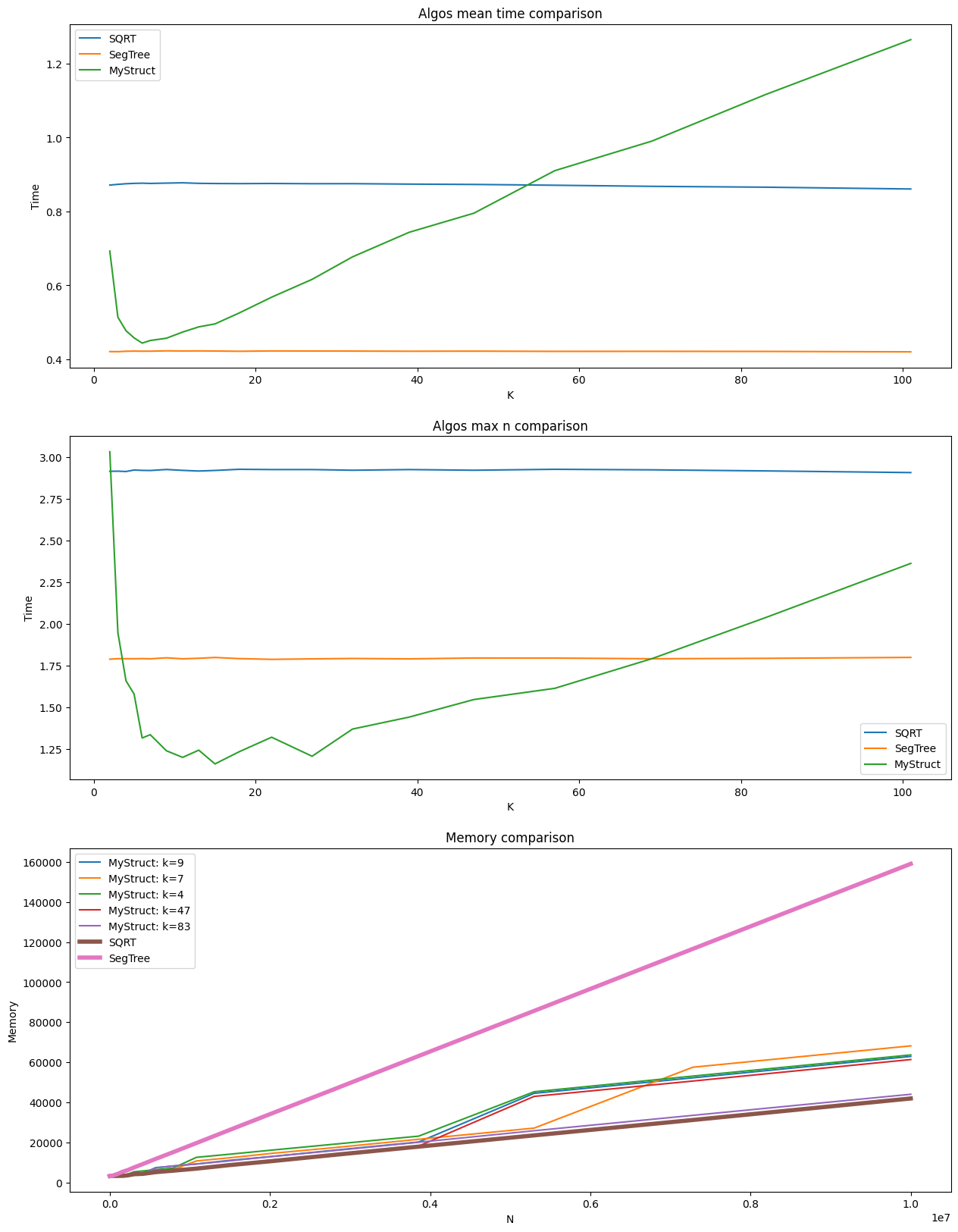
На первом графике изображена зависимость среднего времени работы по всем различным n в зависимости от выбранного k. Так как ДО и корневая не зависят от этого параметра, то они представляют собой константы.

На втором графике изображена зависимость времени работы от k на максимальном тесте, где n = 10'000'000.

На третьем графике можем увидеть зависимость затрачиваемой памяти от количества элементов.

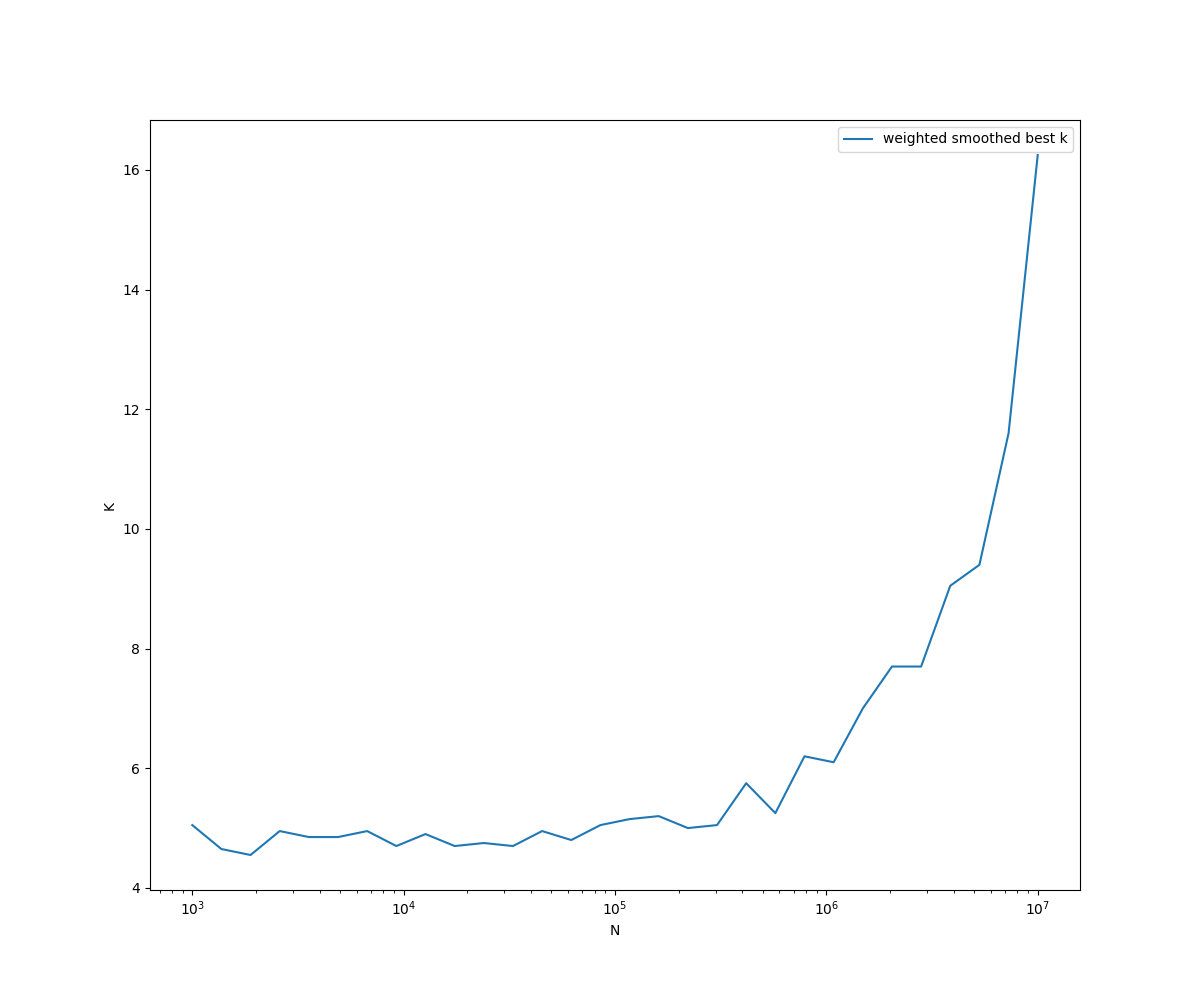
На последнем, изображена зависимость "лучшего" k от количества элементов (использовалось взвешенное среднее по 5 быстрейшим k, чтобы минимизировать выбросы).

Итог

Как мы видим, подход SST имеет выигрыш по памяти (обычно не менее чем в 2 раза). А так же время работы аналогичное ДО, а иногда даже меньшее. И да, понятно, что подобный подход на практике, вероятно, не особо применим в чистом виде, но имеется явная возможность распараллелить вычисления на этом дереве, что требует дальнейшего изучения.

Тем не менее, это мой первый опыт в подобных исследованиях и мной могли быть допущены ошибки, если таковые имеются, буду рад услышать/прочитать ваше мнение и советы.

P.S.

В дополнение ко всему скажу, что теоретически можно для каждой вершины выбирать собственное разбиение, то есть условно для корневой вершины мы рассматриваем 10 потомков (10 блоков), а для какого-нибудь из её сыновей 5 или другое число. То есть число потомков для вершины это некоторая функция f(n), где n - количество элементов за которое отвечает текущая вершина. Сейчас собственно занимаюсь поиском/исследованием этой функции.

Так же если у вас возникают вопросы почти любого характера начиная от неясностей в работе алгоритма до совета, как и где узнать/почитать/послушать про алгоритмы в спортивном программировании, или же вы видите ошибки допущенные мной в процессе анализа алгоритма, буду рад, если вы об этом напишете.